淺析基于FPGA的Mish函數實現

肖祥位 蔡敬菊 徐智勇

1. 中國科學院光電技術研究所國家光束控制重點實驗室 四川 成都 610209；2. 中國科學院光電技術研究所 四川 成都 610209；3. 中國科學院大學 北京 100049

引言

隨著計算機處理能力的提高，神經網絡再次成為人工智能領域的研究熱點。目前主流的方式仍然是基于CPU/GPU對算法進行實現，但由于神經網絡算法具有龐大的計算量，使得在傳統平臺上實現存在實時性不強、功耗過高、體積較大等缺陷，極大地限制了神經網絡算法的落地應用。因此目前該方向的理論研究和實際應用方面存在著較大的脫節。現場可編程門陣列(FPGA)可以通過硬件描述語言對電路進行描述，可以構建大型電路實現并行計算。使用FPGA實現AI算法，極大地加快了計算速度，提高實時性，降低系統功耗。為AI算法落地提供強有力的支撐。

Mish函數是YOLOv4及其衍生版本里面用得較多的一個激活函數，是整個網絡中實現非線性運算的關鍵。Mish函數的使用使得整個網絡檢測效果得到了很大程度的提升，它的非單調平滑性相比于其他激活函數有著更好的表現。想使用FPGA對YOLOv4及其衍生網絡加速則不可避免地要在FPGA上實現Mish函數。本文首先對Mish函數進行介紹，提出幾種不同的實現方案，通過對不同方案的對比分析，最終確定以多折線擬合與查找表組合的方式進行實現。并通過對硬件的實現分析，確定其誤差在較小的范圍，為使用FPGA加速YOLOv4及其衍生網絡奠定基礎[1]。

1 Mish函數簡介

卷積神經網絡中激活函數是對線性卷積輸出的結果進行非線性計算 以此來模擬神經網絡中的神經元模型。Mish函數則是對卷積層的輸出進行非線性激活，以此實現非線性計算。Mish函數的表達式如下：

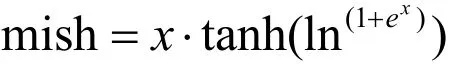
Mish函數是一個非單調函數，其函數圖像如圖1所示。可以看出Mish函數在輸入值小于-10的時候函數值非常接近于0，我們在誤差可以接受的范圍內認為該函數值等于0。在輸入值大于4.7的時候我們可以近似的認為該輸出的值和輸入的值是相同的。我們可以看出輸入值從-10到4.7的過程中，輸出是先減小然后逐漸增大的過程。如果是在FPGA上直接實現Mish函數，則會涉及指數運算、反正切運算以及對數運算。我們都知道這些計算在硬件上實現是非常困難的而且還會消耗大量的計算資源。這在硬件上實現整個YOLOv4算法時完整的實現Mish函數是不可能的。因此我們需要考慮一種簡單、高效的方式來近似Mish的非線性功能。本文通過分析最終采用多折線擬合的形式在硬件上實現Mish函數[2]。

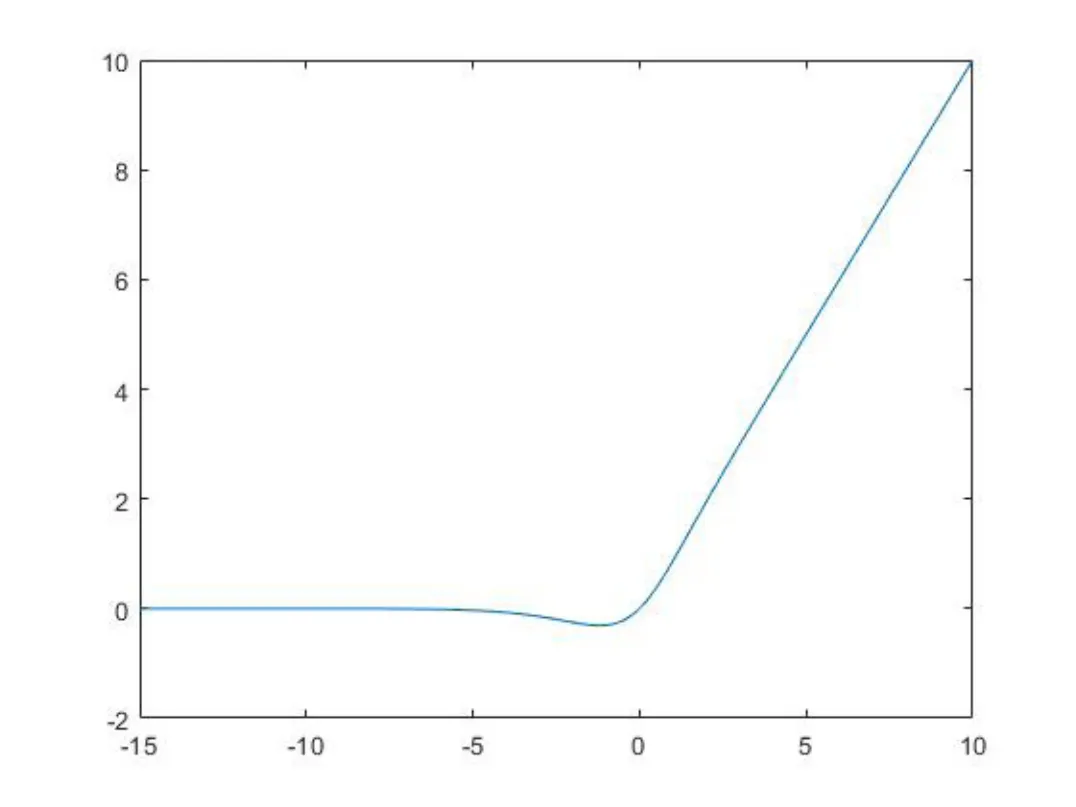
圖1 Mish函數圖像

2 方案選擇

FPGA實現復雜函數常用的方法有：泰勒展開法、查表法、多項式擬合法、分段擬合法、CORDIC算法等。泰勒展開法對于復雜函數時，要保證精度的前提下往往需要展開成多階函數才可以進行擬合，但是在FPGA中展開階數越高實現起來所需要花費的乘法器資源也就越多，在神經網絡中Mish函數的使用往往是并行執行多個相同的乘法，所以在片上DSP資源有限的情況下，我們希望盡可能少的使用DSP,因此使用泰勒展開在實現Mish函數來說耗費乘法器資源過多。基于查表法的FPGA實現是實現復雜算法最方便最快捷的方式，同時查表法還可以達到較高的工作頻率，但是在實現精度要求較高的場合需要較大位寬才能表示，所以需要耗費較大的邏輯資源。基于多項式擬合的方式實現復雜算法，是將算法分成若干段，然后用多項式分別進行擬合，擬合的效果較好可以達到較高的精度，但是仍然存在使用乘法器資源較多的不足。基于CORDIC算法的實現所消耗的資源較少但是耗時較多而且精度不高。基于分段擬合的方式，采用最小二乘法進行擬合，可以將函數分成較多的小區間，在每個區間分別進行擬合，這樣可以保證精度的同時保證使用乘法器資源較少[5]。

本文則是使用分段擬合的方式將函數區間分成若干子區間進行分段擬合，由于保證擬合精度因此分段區間較多，在硬件實現上我們將查找表考慮進來，使用查找表的方式將每個擬合函數的系數存放在查找表中，實現較高頻率的讀取，然后在使用一個乘加器將數據進行計算輸出，保證了較高精度的同時提高了頻率，提升了整體的性能。

3 Mish函數設計

3.1 Matlab擬合

使用matlab對Mish函數進行分段擬合，每段采用最小二乘法進行擬合，使得擬合誤差控制在0.001以下。在誤差允許范圍內當輸入大于4.7時輸出和輸入相等，當輸入在小于-10時我們可以接受輸出等于零，因此只需擬合[-10,4.7]之間的函數值。本文將整個區間分為43個小區間，采用最小二乘法進行分段線性擬合[6]。各區間的擬合如下表所示：

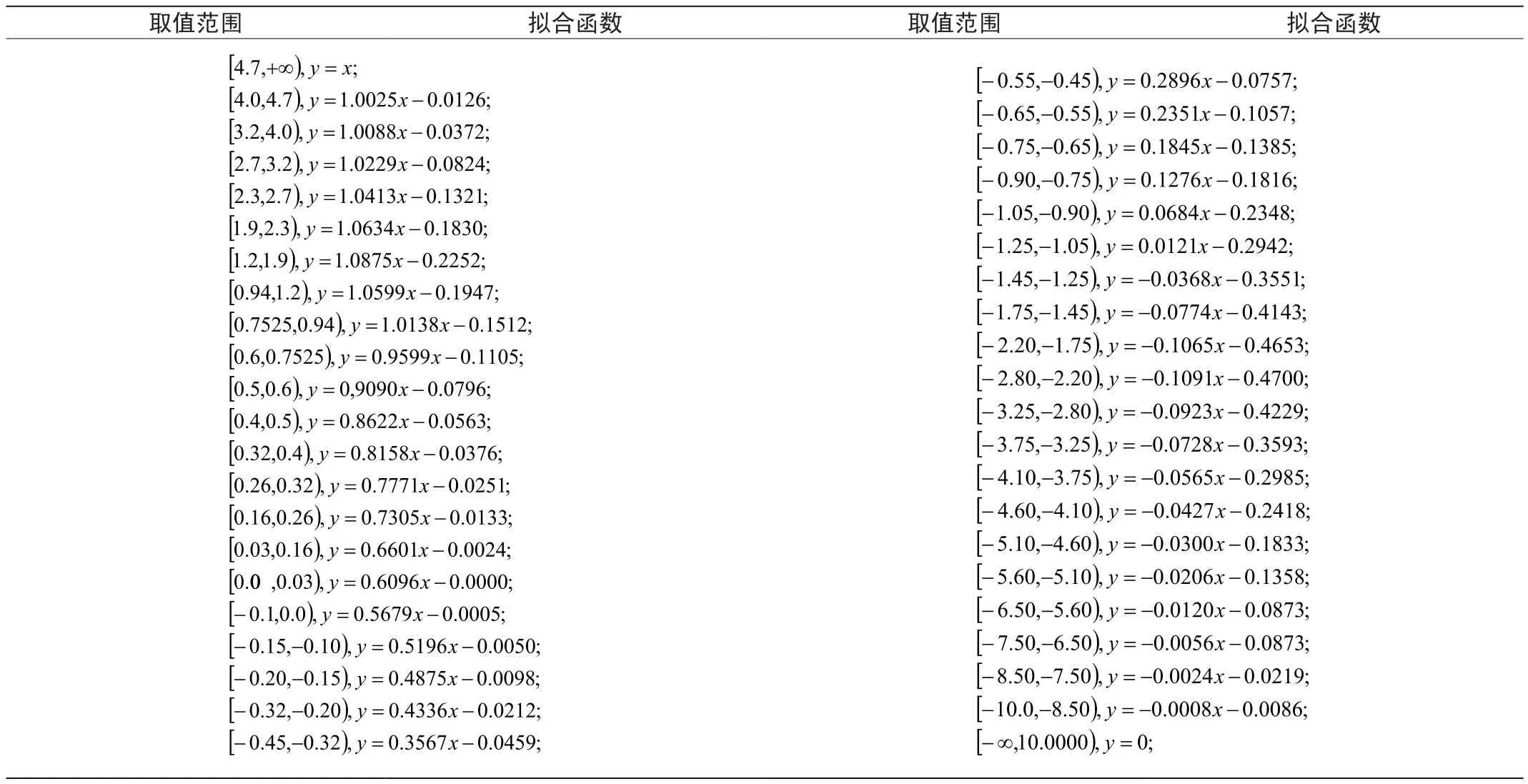
表1 Matlab分段擬合Mish函數

圖2表示的是輸入區間在[-10,10]內，取點間隔為0.01。采用分段擬合的方式將真實值與擬合值做差取得擬合誤差，可以看出本文設計的分段擬合方案與真實的Mish函數非常接近，誤差控制在0.001以下，不會對結果產生誤差[7]。

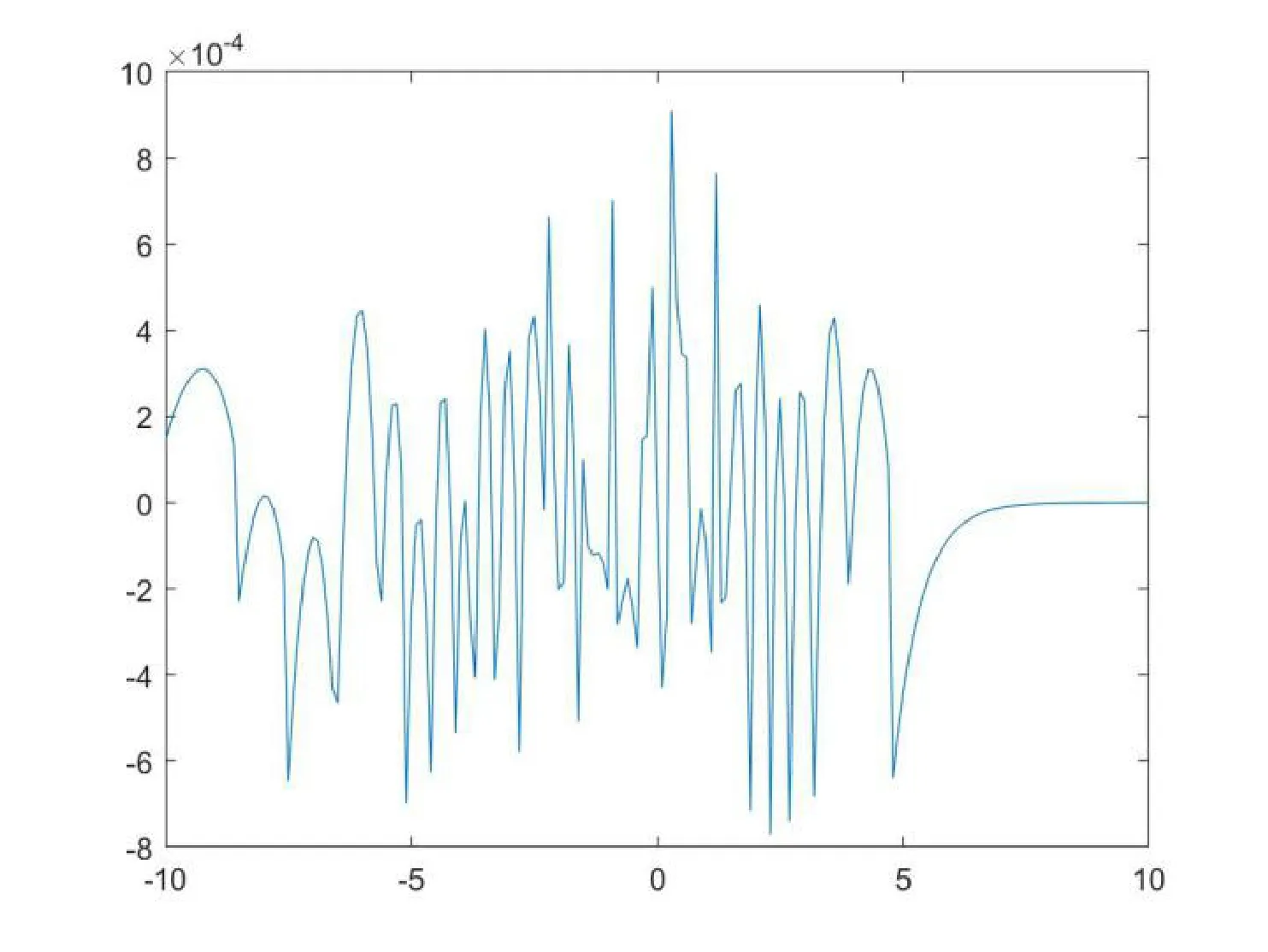
圖2 Mish函數Matlab擬合誤差曲線

在區間[-10,10]內隨機取點15個，得到擬合誤差最大在0.0006，低于0.001。符合我們上面的分析。具體擬合誤差如下表2：

表2 Mish函數隨機取點擬合結果

3.2 FPGA實現

本文采用AC620平臺進行設計實現，一般而言在軟件層面實現Mish函數往往采用32位浮點的形式，但是在FPGA中如果采用浮點計算則會消耗大量的浮點乘法器以及大量的邏輯資源，考慮資源使用率以及運算速度等因素我們將在FPGA上定點小數對Mish函數進行實現，有效的兼顧了資源使用、運行速度。同時我們仿真分析采用16位定點小數的形式實現Mish函數不會對網絡最終分類結果產生誤差。因此我們在FPGA上采用16位定點小數對Mish函數進行實現[8]。

本文采用有符號數的數據進行計算，因此輸入輸出數據第一位為符號位。輸入數據進行量化的過程中將輸入數據同時擴大2048倍，將所有的輸入值進行量化取整以便作為FPGA的輸入。同時也將擬合的所有折線進行擴大2048倍并將所有系數通過四舍五入的形式取整。將這些系數通過建表的方式預先存儲在FPGA內部，當不同輸入進來的時候，對應輸出相應的系數參與計算。這樣極大地保證了系統運行的速度與穩定性。量化以及誤差修正處理后Mish函數在FPGA平臺的擬合函數表達式如下表3：

表3 FPGA擬合Mish函數

運算過程中使用的是有符號數，因此在輸入值進行量化時，將負數的輸入值以補碼的形式進行表示。而在擬合折線的函數表達式中，對輸入值擴大了2048倍，因此需要對其進行右移11位還原為原輸入大小才不會對輸出結果產生影響[3]。

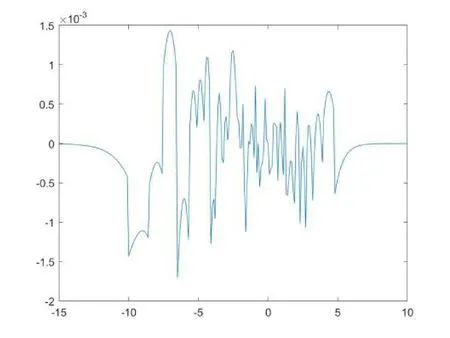
圖3 FPGA擬合Mish函數誤差曲線

如圖3所示，表示了在FPGA上實現Mish函數的誤差，這跟圖2相比有一定的差距，差距主要來源于量化過程中的四舍五入以及對輸入數據的截位處理所產生的誤差。但根據圖3所示的誤差中可以看出，用FPGA擬合后的Mish函數絕對誤差仍然低于0.002。這對我們進行神經網絡的分類精度不會帶來太大的差別。這與表3隨機抽取的15個數據表示結果一致，從表3我們可以看出只有少數點誤差在0.0013左右，但是總體都低于0.002。綜合分析對Mish函數采用上述擬合方案，總體誤差較小均控制在0.002以下，對神經網絡輸出結果無影響[4]。

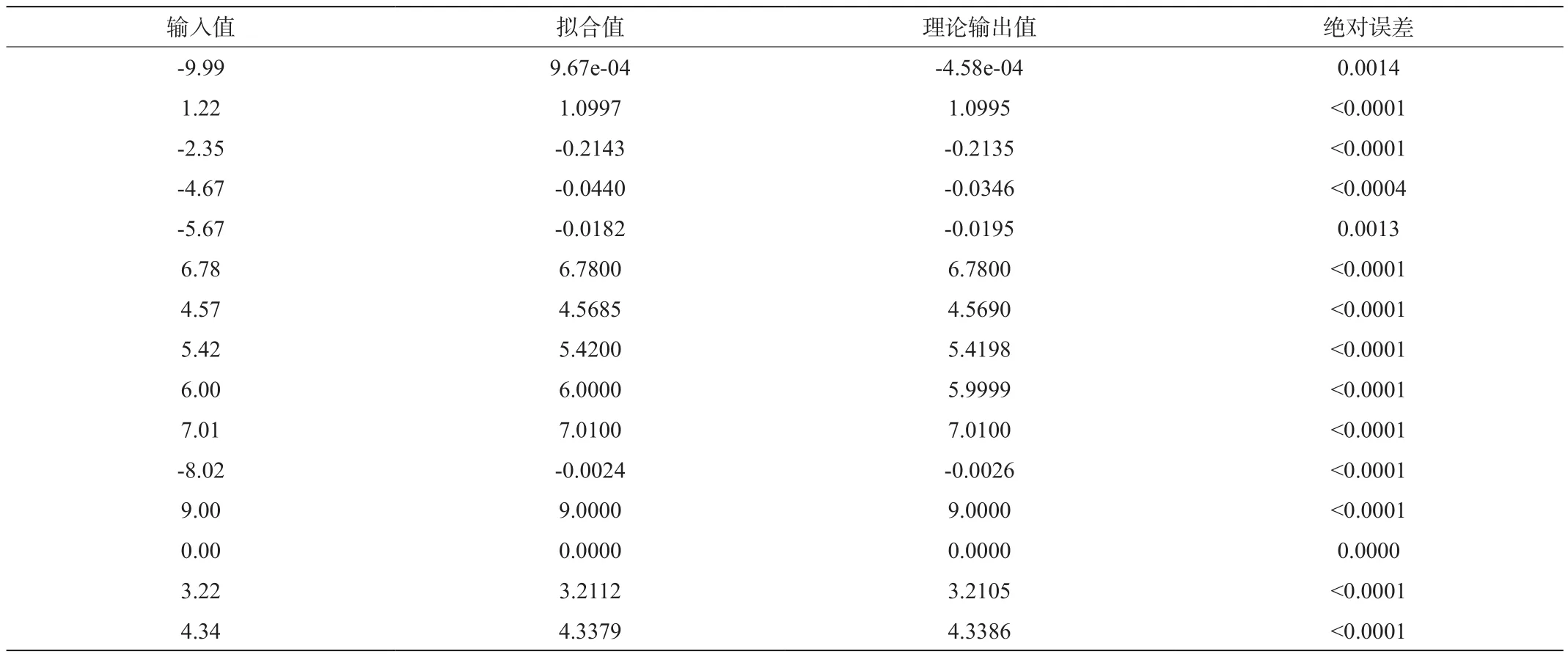
表4 Mish函數隨機取點FPGA擬合結果

具體實現流程框圖如下圖3：

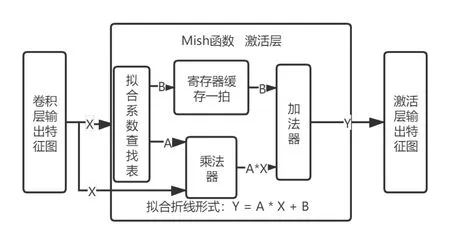
圖4 Mish函數流程框圖

由上圖可以看出我們在卷積層輸出特征后需要經過Mish激活函數,而激活函數具體實現是將擬合的多段折線系數存在查找表中，依據輸入數據的大小，自動匹配對應的系數進行輸出，輸出查找表數據送入乘加器中實現激活函數擬合，最終輸出結果。modulsim仿真結果如圖4所示，我們可以看出完成一次擬合只需要三個時鐘周期，第一個時鐘通過查表取出對應的系數，第二個時鐘周期用于系數與輸入之間的乘法，第三個時鐘則進行常數相加。因此在這種設計模式下只需要三個時鐘周期即可完成一次輸入輸出。整體資源使用情況如圖5所示，我們可以看到整體使用邏輯資源較少，而且每次激活運算只使用一個DSP資源。這對于神經網絡加速來說是非常有利的。采用本文的設計方案在消耗較少資源的情況下可以實現較高的并行度，能更好地提升整體運算速度[9]。

圖4 modulsim仿真結果

圖5 FPGA實現Mish函數整體資源利用

4 結束語

YOLOv4及其衍生版本中，Mish作為激活函數是至關重要的一步，它的優異性能是其他激活函數無法替代的。欲使用FPGA加速YOLOv4及其衍生版本，則不可避免地要在FPGA上實現Mish函數。本文簡單介紹了神經網絡中常用的激活函數Mish，采用分段擬合的方式對該函數進行擬合并在FPGA平臺上對其進行實現。對實現結果與實際結果進行誤差分析，絕對誤差控制在0.002以內，對神經網絡輸出結果不會產生影響。提出一種多折線擬合的方式實現Mish函數，所使用邏輯資源較少，運算速度快，適合在高并行度的神經網絡中使用。對使用FPGA加速YOLOv4以及其他使用Mish函數作為激活函數的網絡有一定的參考價值。