考慮鉆井液流動阻力與鉆柱旋轉的井筒瞬態傳熱新模型

張更，李軍，2，柳貢慧，3，楊宏偉，王江帥，安錦濤

（1.中國石油大學（北京）石油工程學院，北京 102249；2.中國石油大學（北京）克拉瑪依校區，新疆 克拉瑪依 834000；3.北京工業大學，北京 100124）

0 引言

隨著全球的油氣勘探開發逐漸向深水、深層轉移，建井深度逐步加大，隨之而來的是，井下情況更加復雜，這給井筒溫度剖面的計算提出了巨大挑戰。井筒溫度變化對井下壓力控制、鉆井液性能、井壁穩定、井下工具等具有非常顯著的影響，井筒溫度剖面的計算對安全高效的鉆進具有十分重要的意義[1-6]。目前計算井筒溫度的模型主要分為解析模型和數值模型。Holmes等[7]最早對井筒溫度解析模型進行了研究，后來的研究[8-11]多依據他們建立的經典模型，利用解析方法研究在循環鉆進、固井、油氣生產等過程中的傳熱行為。然而，這些解析模型多為穩態模型，不能用于計算復雜系統的傳熱過程，特別是深水和深層鉆井。Raymond等[12-13]進行了開創性的研究，建立了傳熱數值模型并計算了對流換熱系數。之后的一些井筒溫度數值模型都以他們的研究為基礎，只是考慮了深水、停止循環、漏失、氣侵等不同工況環境。井筒溫度受多種因素的影響，現有研究主要集中在鉆井液物性參數、循環時間、鉆井液排量等主觀因素的影響，對鉆井液流動阻力與鉆柱旋轉等客觀因素影響的研究還不夠深入。現有模型沒有同時考慮這2個客觀因素的影響，導致井底溫度計算值偏低，與井底實際溫度偏差較大。所以，建立考慮鉆井液流動阻力與鉆柱旋轉的井筒瞬態傳熱新模型，對比分析流動阻力產生的摩擦熱能與鉆柱旋轉產生的旋轉動能，對研究井筒溫度的影響非常有必要。

1 井筒瞬態傳熱模型

1.1 物理模型

在鉆井過程中，鉆井液以溫度Tin進入鉆柱內，沿著鉆柱向下流動，后通過鉆頭噴嘴進入環空。進入環空后，鉆井液被底部地層加熱，在上返過程中加熱上部地層，最后鉆井液以溫度To從環空井口返出。

在整個過程中，鉆柱內鉆井液、鉆柱壁、環空內鉆井液、井壁（套管或裸眼地層）、地層等控制單元之間，通過熱傳導或熱對流產生能量的傳遞和交換，井筒流動及傳熱物理模型見圖1。在建立考慮流動阻力和鉆柱旋轉的井筒瞬態傳熱新模型時，為了合理簡化計算，依據傳熱特性與流動規律，提出以下假設：1）鉆井液在井筒中的流動為一維單相流動，不考慮其內部物理參數（密度、壓力、速度等）的徑向變化；2）鉆柱壁、套管、水泥環、地層巖石的熱物性參數（導熱系數、密度、比熱容等）保持不變；3）不考慮鉆井液通過鉆頭水眼產生的溫度變化。

圖1 井筒流動及傳熱物理模型

1.2 數學模型

鉆井液在循環過程中，井筒-地層傳熱系統可以視為具有一定邊界條件的熱交換器。依據熱力學第一定律，分別對劃分的5個區域建立控制微分方程。

1.2.1 鉆柱內鉆井液

鉆井液在鉆柱內向下流動過程中，鉆柱內鉆井液控制單元的能量變化由流動阻力產生的摩擦熱能、鉆柱旋轉產生的旋轉動能、軸向上的凈熱量、徑向上與鉆柱內壁的對流換熱量組成。

式中：Qfe為單位長度的摩擦熱能，W/m；Qre為單位長度的旋轉動能，W/m；ρm為鉆井液密度，kg/m3；q 為排量，m3/s；Cm為鉆井液比熱容，J/（kg·℃）；Tp為鉆柱內鉆井液溫度，℃；z為軸向位移，m；rpi為鉆柱內半徑，m；hpi為鉆柱內壁對流換熱系數，W/（m2·℃）；Tw為鉆柱壁溫度，℃；t為時間，s。

1.2.2 鉆柱壁

鉆柱壁連接鉆柱內與環空內的鉆井液控制單元，鉆柱壁控制單元的能量變化由鉆柱壁軸向上的導熱量、鉆柱內壁與鉆柱內鉆井液的對流換熱量、鉆柱外壁與環空內鉆井液的對流換熱量組成。

式中：kw為鉆柱壁導熱系數，W/（m·℃）；rpo為鉆柱外半徑，m；hpo為鉆柱外壁對流換熱系數，W/（m2·℃）；Ta為環空鉆井液溫度，℃；ρw為鉆柱壁密度，kg/m3；Cw為鉆柱壁比熱容，J/（kg·℃）。

1.2.3 環空內鉆井液

鉆井液在環空內向上流動過程中，環空內鉆井液控制單元的能量變化由流動阻力產生的摩擦熱能、鉆柱旋轉產生的旋轉動能、軸向上的凈熱量、徑向上與鉆柱外壁和井壁的對流換熱量組成。

式中：rci為套管內半徑，m；hci為井壁對流換熱系數，W/（m2·℃）；Tc為套管溫度，℃。

1.2.4 井壁

在實鉆過程中，井壁可分為上段套管井壁和下段裸眼井壁。井壁控制單元的能量變化由軸向上的導熱量、井壁與環空內鉆井液的對流換熱量、徑向上與地層或水泥環的導熱量組成。

式中：kc為套管導熱系數，W/（m·℃）；rco為套管外半徑，m；kf為地層導熱系數，W/（m·℃）；Tf為地層溫度，℃；ρc為套管密度，kg/m3；Cc為套管比熱容，J/（kg·℃）。

1.2.5 近井壁區域

近井壁區域主要由水泥環、套管、地層組成，其能量變化主要考慮軸向和徑向上的導熱量。

式中：T為介質的溫度，℃；r為徑向節點距離中心軸的距離，m；ρ為介質的密度，kg/m3；C 為介質的比熱容，J/（kg·℃）；k為介質的導熱系數，W/（m·℃）；下標 j代表徑向節點序號，徑向上共劃分13個節點。

根據Holmes的觀點，地層對井筒溫度的影響半徑為3 m左右。由此，在劃分徑向網格時，設定5≤j≤13。其中，5≤j≤7為套管和水泥環的組合體，7＜j≤13為地層。

對流換熱系數h的計算公式為

式中：km為鉆井液導熱系數，W/（m·℃）；d 為水力當量直徑，m；Re為雷諾數；Pr為普朗特數。

流動阻力產生的摩擦熱能與鉆柱旋轉產生的旋轉動能的計算公式為

式中：pf為鉆井液的流動阻力，Pa；f為摩擦因數，與管壁粗糙度、雷諾數、流性指數有關；vm為鉆井液流速，m/s；Ek為旋轉動能，J；Δt為時間步長，s；Δz為軸向位移步長，m；I為鉆柱的轉動慣量，kg·m2；ω 為鉆柱轉速，r/min；mp為鉆柱質量，kg。

1.3 模型初始及邊界條件

1.3.1 初始條件

1）整個系統初始時刻的溫度為地層溫度。

式中：Ti（z，0）為初始時刻i區域在軸向位移z處的溫度，℃；Ts為地表溫度，℃；G 為地溫梯度，℃/m；下標i代表劃分的5個區域。

2）鉆柱井口溫度 Tp（0，t）為注入溫度Tin。

1.3.2 邊界條件

1）在井底時，鉆柱內鉆井液、鉆柱壁、環空內鉆井液的溫度相等。

式中：L為井底深度，m。

2）地表邊界為絕熱邊界；離井筒以外一定距離的地層不受干擾，為原始地溫；在井壁處，傳入環空的熱量與流出地層的熱量相等。

2 模型求解與對比

為了節省計算時間，在徑向上采用結構化非均分網格對系統進行離散。為了提高計算的穩定性，采用有限差分法的全隱式格式對控制微分方程進行離散。空間上，依據從左到右、從上到下的順序；時間上，依據從小到大的順序，依次進行離散，構成線性方程組[14-17]。方程組利用高斯-賽爾德迭代法進行求解。

各控制單元的微分方程離散后，都可以寫成如下形式：

式中：αij，βij，γij，δij，ξij分別為常系數項；Cij為方程常數項；T的上標代表時刻，下標代表節點位置。

各節點的離散方程組成的線性方程組可以由矩陣表示：

式中：A 為系數矩陣；Tn，Tn+1為所有 n，n+1時刻節點溫度組成的向量。

利用文獻[18]中的數據（見表1），將本文模型的計算值分別與 Yang[18]數值模型和 Al-Saedi[19]解析模型的計算值進行對比，結果如圖2所示。

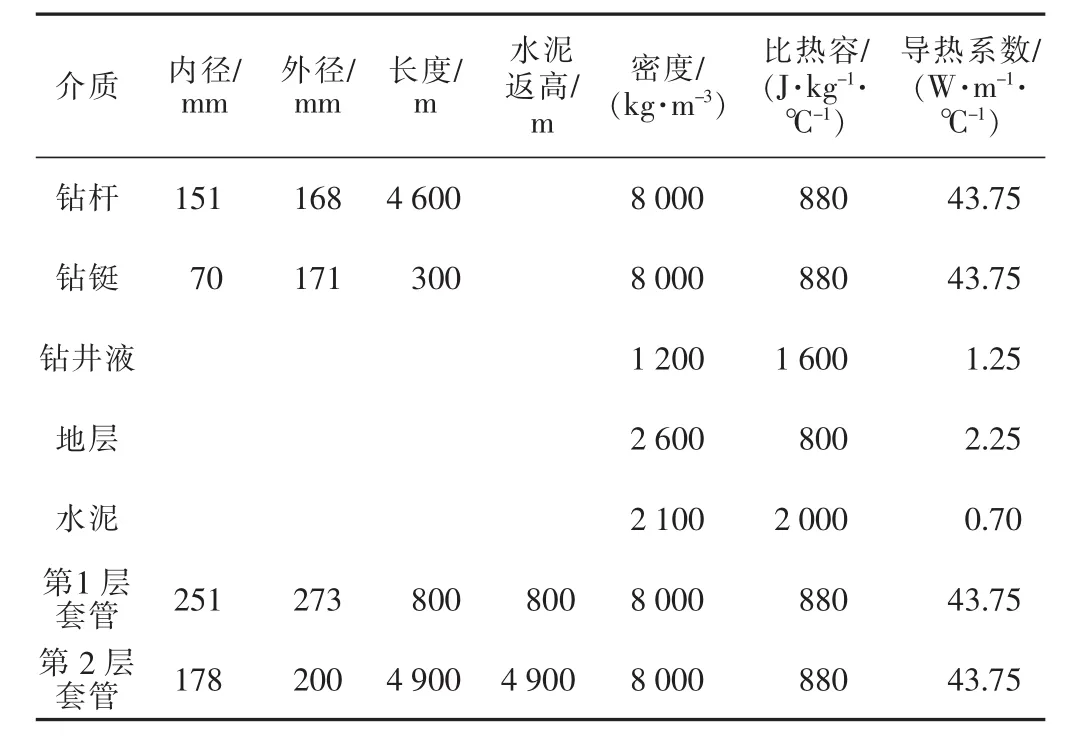
表1 模擬井基本參數

圖2 模型對比示意

從圖2可以看出，本文模型的計算值分別比Yang數值模型與Al-Saedi解析模型的計算值高出約5℃和3℃，更接近井底實際溫度。這主要是由于Yang數值模型沒有考慮鉆柱旋轉產生的旋轉動能、Al-Saedi解析模型沒有考慮鉆井液流動阻力產生的摩擦熱能的影響導致的。

3 實例分析

某井為一口直井，三開鉆頭直徑215.9 mm，井深4 600 m，鉆柱轉速120 r/min，鉆柱井口注入溫度25℃，地表溫度16℃，地溫梯度0.023℃/m。鉆井液的流變參數、井身結構及鉆具組合參數、各介質的熱物性參數如表2—4所示。

表2 鉆井液流變參數

表3 井身結構及鉆具組合參數

表4 各介質熱物性參數

3.1 流動阻力與鉆柱旋轉對環空溫度的影響

為了分析流動阻力與鉆柱旋轉對井筒溫度分布的影響，分別計算了考慮流動阻力或鉆柱旋轉時，循環8 h后的井筒環空溫度剖面（見圖3）。

圖3 不同熱源情況下的環空溫度剖面

從圖3可以看出，隨著井深的增加，環空溫度呈現先增加后降低的趨勢。這是由于，底部地層的熱量不斷被鉆井液帶出加熱上部地層，隨著考慮的熱源情況增多，環空溫度也不斷地增加。其中，考慮鉆柱旋轉的環空溫度比考慮流動阻力時要大。

隨著井深的增加，不同熱源情況下的環空溫度差（與不考慮流動阻力與鉆柱旋轉的環空溫度相比）越來越大，特別是井深超過3 000 m后，環空溫度差增加的幅度急劇增大（見圖4）。這主要是因為該井套管下深為3 000 m，套管的導熱系數比地層的導熱系數要大得多，導致鉆井液在上返過程中與周圍地層進行大量的熱交換，井筒內的溫度快速下降，致使上部井段溫度差異不大。考慮鉆柱旋轉時，在4 000 m以下環空溫度差增加的幅度較小，這是由于4 000 m以下為鉆鋌段，鉆鋌的內徑比鉆桿小，轉動慣量比鉆桿低，導致旋轉動能降低，環空溫度差增加的幅度變小。

圖4 環空溫度差隨井深的變化

3.2 流動阻力與鉆柱旋轉對井底、井口溫度的影響

通過研究流動阻力或鉆柱旋轉對井底溫度的影響，發現隨著循環時間的增加，井底熱量不斷被鉆井液循環帶出，井底溫度逐漸降低（見圖5）。考慮流動阻力或鉆柱旋轉的井底溫度，始終比不考慮流動阻力與鉆柱旋轉的井底溫度要高。考慮流動阻力的井底溫度差約為3℃，考慮鉆柱旋轉的井底溫度差約為6℃，同時考慮流動阻力與鉆柱旋轉的井底溫度差約為10℃。這說明鉆柱旋轉對井底溫度的影響比流動阻力要大。

圖5 井底溫度隨循環時間的變化

圖6為不同熱源情況下井口溫度隨循環時間變化的關系曲線。從圖6可以看出，隨著循環時間的增加，井口溫度不斷增加。考慮流動阻力時，井口溫度能達到29.5℃左右；考慮鉆柱旋轉時，井口溫度可達30.0℃左右；同時考慮流動阻力與鉆柱旋轉，井口溫度增加2℃左右。這說明鉆柱旋轉對井口溫度的影響比流動阻力要大。

圖6 井口溫度隨循環時間的變化

3.3 鉆柱轉速與鉆井液排量對環空溫度的影響

隨著鉆柱轉速的增加，鉆柱的轉動慣量逐漸增加，繼而產生的旋轉動能不斷增大，導致環空溫度增加（見圖 7）。

圖7 不同轉速的環空溫度剖面

鉆井液排量同時影響鉆井液流動阻力及對流換熱系數。排量較小時，主要影響對流換熱系數，隨著排量的增加，對流換熱加快，下部地層溫度降低，上部地層溫度上升；排量較大時，主要影響鉆井液流動阻力，隨著排量的增加，流動阻力產生的摩擦熱能增加，環空溫度增大。如圖8所示，隨著排量的增加，環空溫度不斷增加，且增加的幅度不斷增大。

圖8 不同排量的環空溫度剖面

4 結論

1）相比不考慮流動阻力與鉆柱旋轉的影響，鉆井液流動阻力和鉆柱旋轉對井筒溫度剖面的影響較大，且隨著井深增加，這種影響逐漸加劇，特別是在裸眼段。

2）相比流動阻力，鉆柱旋轉對井口溫度和井底溫度的影響更為明顯。但是，流動阻力與鉆柱旋轉對上部井段溫度的影響幅度并不大。

3）隨著鉆柱轉速的增加，鉆柱旋轉產生的旋轉動能增大，環空溫度不斷增加；隨著鉆井液排量的增加，流動阻力產生的摩擦熱能增加，環空溫度逐漸增加，且增加的幅度逐漸增大。