現代有軌電車車輛獨立輪對與傳統輪對曲線導向能力分界點計算

周 橙 池茂儒 雷昆來 孫代濤

（1.中車青島四方機車車輛股份有限公司，266111，青島；2.西南交通大學牽引動力國家重點實驗室，610031，成都∥第一作者，工程師）

現代有軌電車為了實現100%低地板化，其列車多采用獨立輪對結構。獨立輪對取消了剛性車軸，左右車輪不再耦合，具有橫向穩定性好、小半徑曲線通過能力較強等優點；但同時，獨立輪對失去了傳統輪對的直線對中與曲線導向能力。國外很早就對獨立輪對導向原理進行了研究［1］；國內同樣有多位學者對獨立輪對的蠕滑機理與導向機理進行了深入探究［2-6］，文獻［7］還指出了傳統輪對在小半徑曲線運行時存在自導向能力惡化的現象。

至今在相關的獨立輪對動力學研究中，雖然指出了其缺乏導向能力與傳統輪對小半徑曲線下導向能力惡化等現象，但并沒有對傳統輪對與獨立輪對性能分界進行明確分析與深入研究。本文將以單輪對純滾線分析方法與整車動力學仿真方法，對傳統輪對與獨立輪對曲線導向能力分界點進行計算，為后續關于獨立輪對導向方式的設計提供參考。

1 傳統輪對與獨立輪對導向原理

傳統輪對左右車輪固結在同一車軸上，相互之間無法轉動，轉速相同，是剛性輪對；獨立輪對左右車輪可以相對獨立地繞車軸旋轉，轉速解耦，車軸可以做成曲軸形式從而降低車輛地板面高度，是現代有軌電車低地板列車的常用輪對形式。

傳統輪對與獨立輪在動力學性能上的主要區別就在于導向能力。鐵道車輛導向主要是依靠輪軌接觸力中的重力復原力、橫向蠕滑力和縱向蠕滑力［11］。

輪軌的法向力由于輪軌接觸面傾角所形成的水平橫向分力為重力復原力。傳統輪對與獨立輪對均存在重力復原力，而獨立輪對增強導向能力的措施之一就是增大左右車輪的輪軌接觸較差。左右車輪重力復原力合力可以表示為

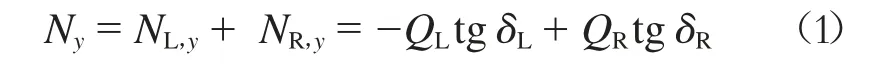
式中：

Ny——法向力的水平橫向分力，即重力復原力；

Q——法向力的豎向分力，即輪重；

δ——輪軌接觸角；

NL，y——左車輪的重力復原力；

NR，y——右車輪的重力復原力。

蠕滑力主要包括縱向蠕滑力、橫向蠕滑力和自旋蠕滑力。設dy、ψ、φ 分別為輪對的橫移量、搖頭角、側滾角，d0為輪軌接觸點橫向距離之半，λ 為錐度，f11、f22均為Kalker 蠕滑系數。

對于傳統輪對，左右車輪轉速相同，忽略自旋蠕滑，可以得到橫向蠕滑力合力Ty與縱向蠕滑力矩

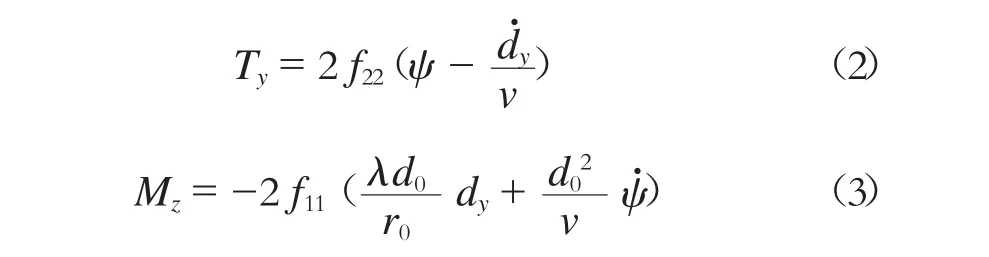
式中：

v——車速；

r0——車輪名義滾動圓半徑。

傳統輪對Ty主要由搖頭運動產生，而Mz主要由橫移運動產生。

對于獨立車輪輪對，左右車輪線速度基本相同，轉速差無法產生縱向蠕滑力，忽略自旋蠕滑，可得

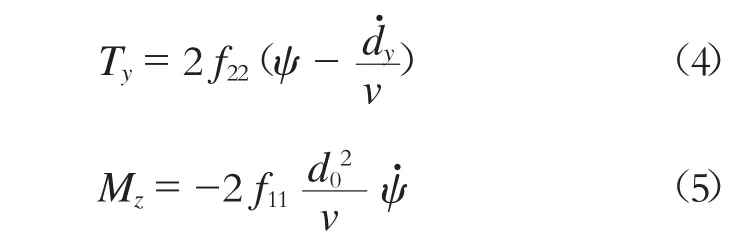
獨立車輪輪對Ty同樣主要由搖頭運動產生，但縱向蠕滑力近似為零，難以形成有效的Mz。

圖1 所示為傳統輪對與獨立輪對導向原理。結合式（2）～（5），從圖1 中可以看出兩種輪對導向過程分別為：

1）傳統輪對出現如圖1 a）所示橫移后，會產生順時針的縱向蠕滑力矩，促使輪對出現順時針搖頭；當輪對出現如圖1 a）所示搖頭運動后，產生橫向蠕滑力促使輪對向軌道右側運動。在運行中，橫移與搖頭同時出現，輪對會出現以正弦式的運動回到軌道中心線的趨勢，即輪對的自動對中和曲線導向。

2）獨立輪對出現圖1 b）所示的橫移之后，無法形成縱向蠕滑力與縱向蠕滑導向力矩，但搖頭可以產生橫向蠕滑力促使輪對向右運動。在這樣的輪軌力條件下，輪對出現橫移與搖頭后無法恢復，不存在蛇行運動，但同時失去了曲線導向能力，直線工況下也無法對中。

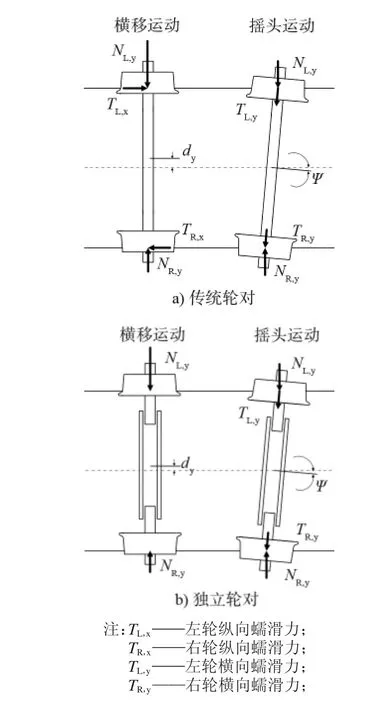
圖1 傳統輪對與獨立輪對導向原理圖

2 單輪對導向分界點理論分析

單輪對以速度v 通過半徑為R 的曲線，曲線超高角為α。除受到輪軌力外，輪對還受到一系懸掛縱向作用力Fx，f與一系懸掛橫向作用力Fy，f。在僅考慮輪對位移的條件下，一系懸掛縱向作用合力為搖頭力矩Kpψ，Kp為一系懸掛搖頭剛度；一系橫向作用合力為Kp，ydy，Kp，y為一系懸掛橫向剛度。重力復原力Ny可以簡化為Krdy，Kr為簡化后的重力復原剛度。設M 為輪對總質量，g 代表重力加速度，Iψ，z為輪對搖頭慣量，Iy為單個旋轉車輪的點頭慣量。

現以傳統輪對為例，對輪對曲線通過時的受力進行分析，如圖2 所示。根據受力分析可以建立輪對的導向動力學方程。

結合式（2）、（3），可以得到曲線條件下傳統輪對的導向方程為：

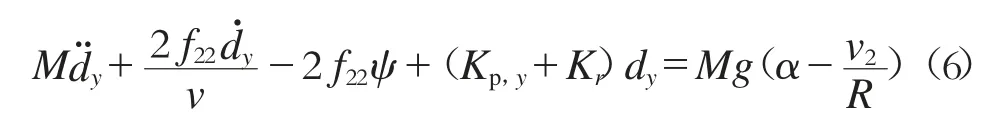
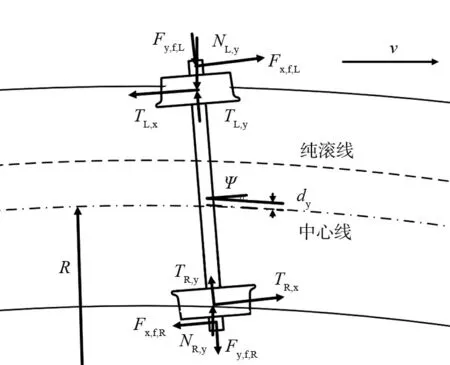
圖2 單輪對曲線通過受力分析

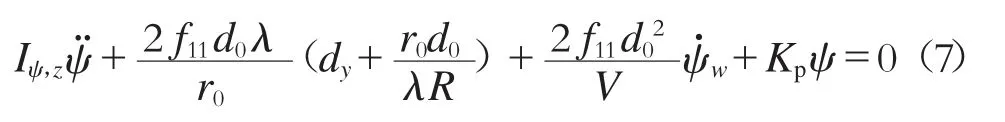
考慮理想條件，當列車穩態通過曲線時，忽略慣性項d¨y，i、ψ¨i，橫移速度項d˙y，i與搖頭角速度項˙ψi為0，當且僅當Kp=0 的情況下，傳統輪對處于純滾線位置運動。由式（7）可以得到純滾線位移量為

具有一定錐度的輪對產生橫移后，車輪滾動半徑會發生改變。同樣的轉速下，當左右車輪滾動距離差可以完全彌補曲線內外軌路程差時，輪對處于純滾線位置，此時縱向蠕滑力最小。

當輪對橫移處于純滾線以內時，會產生負向的縱向蠕滑力矩，驅使輪對負向搖頭，進而產生負向的橫向蠕滑力，輪對趨向于曲線外側運動；反之，輪對橫移處于純滾線以外時，會產生正向的縱向蠕滑力矩，驅使輪對正向搖頭，輪對趨向于曲線內側運動。傳統輪對最終趨向于純滾線進行運動。

同樣，對于獨立輪對，只考慮主要位移因素，設˙β為車輪轉速差之半，忽略較小量，通過簡化變形，可以得到獨立輪對在曲線上的橫移與搖頭方程為：

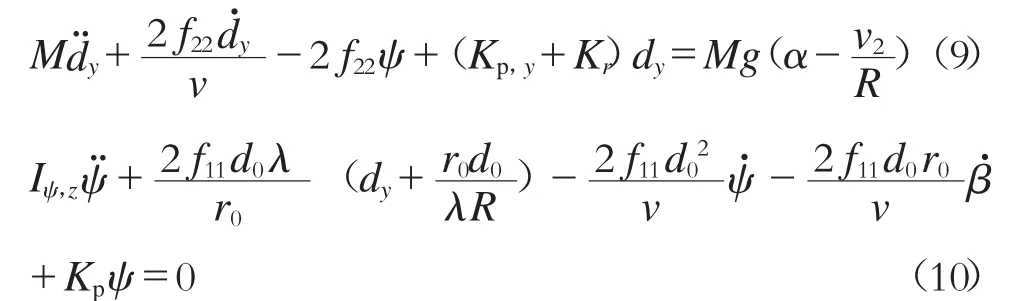
獨立輪對缺乏縱向蠕滑力，穩態曲線通過時橫向位置最終會依靠踏面達到一個各力平衡的位置，基本上都處于輪對最大橫移位置。

現代有軌電車車輪輪對最大橫移量在6 mm 左右，6 mm 以上時可能會出現輪緣貼靠與多點接觸。假設輪對只有橫移，以6 mm 為純滾線位置，可以得到λ 與對應R 關系如圖3 所示。

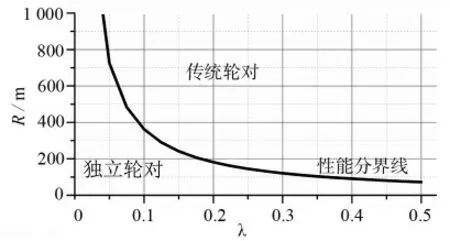
圖3 λ 與R 關系

由于傳統輪對始終有趨向于純滾線運動的趨勢，最大橫移位置對應的純滾線即為輪對性能分界曲線。當曲線半徑大于分界曲線半徑時，傳統輪對性能更優；反之，獨立輪對曲線通過性能更優。

采用現代有軌電車典型踏面為例，其輪軌關系如圖4 所示，以此分析低地板列車常用曲線半徑下的純滾線位置。輪對最大橫移量為6 mm，λ 為0.314，大于6 mm 時，λ 統一按照0.314 計算。各R與各λ 對應純滾線橫移量結果如表1 所示。

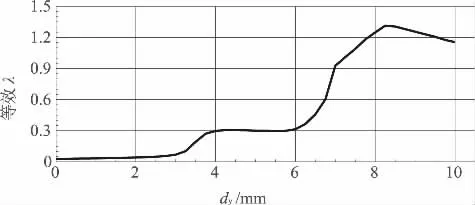
圖4 輪軌關系

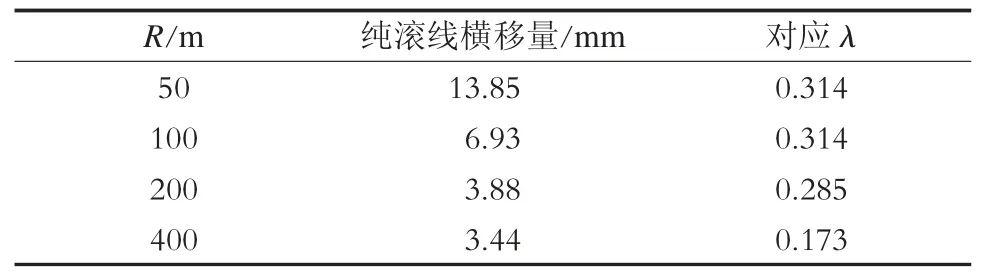
表1 不同曲線半徑下純滾線橫移量

純滾線所對應的最大橫移位置的工況成為了傳統輪對與獨立輪對曲線通過性能的分界點，輪對最大橫移量6 mm 所對應的R 為117 m。對于λ 與本例相似的輪軌關系，分界點可以擴展為R=100 ～200 m 區域。

3 整車導向分界點仿真分析

采用應用最為廣泛的五模塊浮車型式的低地板列車進行整車動力學分析。采用Simpack 軟件建立五模塊低地板列車動力學模型。

其車體、構架考慮6 個自由度，軸箱考慮點頭自由度。傳統輪對考慮6 個自由度，軸橋考慮6 個自由度，獨立旋轉車輪為點頭旋轉自由度。傳統輪對列車模型系統自由度為96，獨立輪對列車模型系統自由度為108。建立一系、二系懸掛與車間懸掛。整車動力學模型如圖5 所示。

曲線設置為右向曲線，取R 分別為400 m、200 m、100 m 及50 m 進行分析。對比傳統剛性輪對與獨立輪對在導向性能上的區別，包括一位輪對的橫移量、搖頭角與脫軌系數，如圖6 所示。

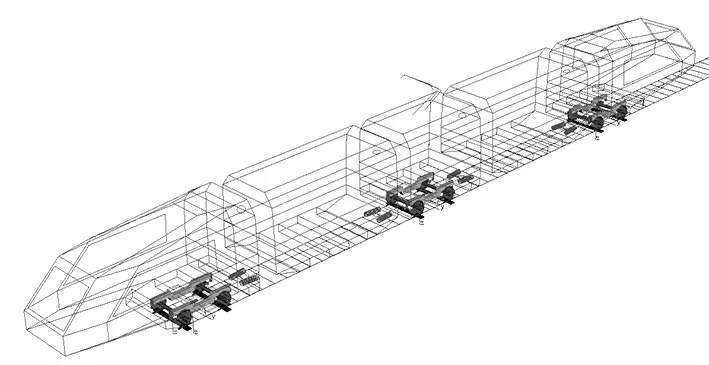
圖5 現代有軌電車低地板列車動力學模型

圖6 a）、b）分別為R=400 m、R=200 m 曲線通過性能對比。可以看到，雖然傳統輪對的曲線通過能力優于獨立輪對，但隨著曲線半徑的減小，兩者導向性能逐漸接近。

圖6 傳統輪對與獨立輪對的列車導向能力對比

圖6 c）、d）為R=100 m、R=50 m 曲線下兩種輪對的曲線通過性能對比。此時輪對的最大橫移量已經不足以滿足純滾線的要求，傳統輪對趨向于曲線外側運動，而獨立輪對自然形成的轉速差反而會減弱這種趨勢，從而表現出更優的導向性能。隨著曲線半徑的減小，獨立輪對的優勢更加明顯，R=50 m 時脫軌系數小了0.2 左右。

在脫軌系數對比下，兩種輪對的性能分界點更加接近R=200 m 的曲線。造成這種差異的原因在于輪對并非自由輪對，會受到列車懸掛及姿態的影響，使傳統輪對進行曲線導向時更加艱難，從而導致分界點會趨向于更大半徑的曲線。

由以上分析可知，雖然整車導向性能分界半徑上與單輪對純滾線結果略有差異，但所得到的分界點仍然為R=100 ～200 m 區域。

4 結論

1）傳統輪對通過曲線時始終趨向于純滾線運動，而獨立輪對由于缺乏導向力會處于最大橫移量位置。假設輪對處于最大橫移量位置，可以得到傳統輪對與獨立輪對的性能分界線。采用典型踏面進行分析，純滾線對應最大橫移量位置時為傳統輪對與獨立輪對曲線通過性能的分界點，為曲線R=100 ～200 m 區域。

2）建立現代有軌電車低地板列車模型，對不同曲線工況下傳統輪對與獨立輪對的整車條件下的導向能力進行分析。在典型踏面下，雖然整車導向性能分界半徑上與單輪對純滾線結果略有差異，但所得到的分界點仍然為R=100 ～200 m 區域。