粗糙集屬性依賴度強化的應急數據挖掘模型

高天宇，王慶榮，楊 磊

蘭州交通大學 電子與信息工程學院，蘭州730070

在大數據時代，數據挖掘作為一種有效的數據處理手段，能夠幫助決策者從數據中發掘有助于決策的信息[1]。粗糙集理論不需要先驗知識，作為處理模糊信息的有效方法，在挖掘數據中的隱藏信息時有明顯優勢，常用于數據預處理或數據分析[2-3]。屬性約簡作為粗糙集理論中的重點方法，通過依賴度計算來去除冗余屬性[3]。Raza 等[4]通過直接計算屬性依賴度進行屬性約簡，比較經典方法，其精確度得到了提高；針對不同情況的樣本數據變化情況，Shu 等[5]通過增量式計算給出了相應的約簡算法；關于粒計算理論在數據處理及粗糙集的使用中，Liang 等[6]引入高斯核函數粒化數據，提高了大數據集的處理效率；Qian等[7]分析了從多粒度層面考慮問題的屬性約簡的有效性；張天瑞等[8]基于粗糙集與決策樹的數據挖掘方法，給出了關于全斷面掘進機的一種故障檢測新途徑；劉穎超等[9]基于一種新的粗糙集屬性約簡理論，挖掘了影響刀具磨損的關鍵因素；邵為爽等[10]結合粗糙集與BP 神經網絡，給出一種新的煤炭物流中心選址方法。

分析震后經濟損失與其影響因素的相關程度是合理經濟損失預測及分析的前提，有效的地震直接經濟損失評估，對救災、財政、捐助、理賠等有重要意義[11]。劉如山等[12]通過建筑類型、數量、空間分布、結構易損特性以及地震烈度計算地震經濟損失；陳堯等[13]選取震級和烈度對直接經濟損失進行了評估；王偉哲[11]理性分析地震的致災因子和承災因子，選取了地震震級、震源深度、設計基本加速度、災區面積、全國人均GDP和受災人口的乘積，作為神經網絡的輸入變量及預測經濟損失的影響因素；趙士達等[14]通過理性分析選取了震級、震源深度、受災面積、受災人口、設計基本地震加速度、地區人均GDP和產業結構比例作為影響因素；和仕芳等[15]選取震級、烈度、人均GDP、人均財政收入、農民人均純收入作為影響因素，并從時間特征總結出，經濟和人口差異是地震災害之間經濟損失明顯差異的重要影響因素，從數據中發現各影響因素與經濟損失存在線性關系。

傳統的地震經濟損失分析中缺少對于相關影響因素的分析，影響因素的使用趨于主觀選取，影響因素之間重要性研究較少。地震數據特點較復雜，挖掘影響因素的隱藏信息是分析影響因素間重要性的關鍵。基于粗糙集理論進行重要信息的挖掘較適合于地震數據分析，合理的數據分析將有助于預測、救援及經濟市場的運作。屬性約簡作為粗糙集的核心[16]，其約簡原理主要依賴于條件屬性對于決策屬性的重要性的區別[2]。關于震后經濟損失的相關數據，在傳統的屬性約簡方法中，決策矩陣條件屬性較多時，隱藏其中的低依賴度屬性增多、屬性值粒度較小，導致條件屬性的重要性一致，造成約簡困難。粒計算作為大數據分析的新方法，粒化準則的確定、分析數據的多粒度視角都有待進一步研究[3]，常見的無監督離散化方法有等寬、等頻、近似等頻、密度、聚類等[17-18]。為解決約簡困難給出一種依賴度強化方法，為將其合理化，結合多粒度粗糙集給出一種離散化方法。

給出一種數據挖掘模型，引入多粒度粗糙集，給出合理的粒化準則并從多角度分析數據。在數據挖掘模型中首先提出一種探索模型，確定粒化準則、探索粒度范圍與屬性組合范圍。然后考慮粒度范圍與離散量范圍、粒化準則與離散量的關系，根據范圍內不同的離散量離散化數據；考慮多種條件屬性組合與決策屬性的關系，在屬性組合范圍內全組合屬性，計算組合的屬性依賴度。最后強化屬性依賴度，將不同屬性之間的依賴程度從組合提取至屬性本身。在本文搜集的國內5 級以上地震的數據中，成功挖掘了震后經濟損失的重要、次要影響因素，且與傳統方法相比更有效。

1 多個次要屬性引起的屬性約簡困難

1.1 粗糙集屬性依賴度

使用粗糙集處理信息時首先將處理的信息表示為一個四元組T={U,A,V,f}。其中，U={x1,x2,…,xn}為論域或對象集合，是全體樣本的集合；A={A1,A2,…,Ac,Ad}為屬性集合，其中包含條件屬性C={A1,A2,…,Ac}、決策屬性D={Ad}，V代表了屬性值的集合，V={a11,a12,…,and}。f代表一個信息函數，通過此函數來確定樣本與屬性所對應的屬性值，即f(x,A)=V。條件屬性等價類集合為條件類，決策屬性等價類集合為決策類。

E為U中的一組等價關系，x∈U為條件類對象，X∈U為決策類對象，X關于E的上近似E*與下近似E*分別為：

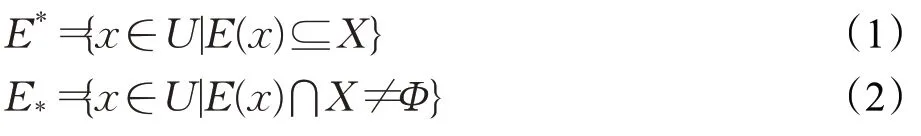
利用屬性依賴度來定義決策屬性與條件屬性的關聯程度，將依賴程度表示為以下表達式：

1.2 決策矩陣中隱藏多次要屬性

根據粗糙集的四元組T={U,A,V,f}，給出屬性約簡的決策表Td={U,A,C,D}，屬性集A中劃分出條件屬性集C與決策屬性集D。判斷某條件屬性Ac∈C對于決策屬性Ad∈D的依賴程度，計算Ac的剩余屬性依賴度Ro(C,D|C-Ac)，得到剩余屬性依賴度集合R，當某屬性對應剩余屬性依賴度較低時，屬性較重要，反之較次要。

在屬性約簡決策矩陣中，存在多個次要條件屬性時，會導致屬性值粒度過小，根據等價類的定義，此時易出現等價類過少，甚至沒有等價類的情況。例如：某決策表中條件類為{{x1},{x2},…,{xn}}，該類中無等價類，決策類為{{x1,x2,x3},{x4,…,xn}} ，選取{x1,x2,x3} 為決策集合，R中的值可能均為3n。過多的次要屬性使得Ac的變化很難引起上近似集變化，若所有Ac對應剩余屬性的依賴度均沒有變化，則難以約簡。

變精度粗糙集放寬對上下近似集的定義[19]，模糊了粗糙集的邊界，使得Ac的變化對于其剩余屬性依賴度的影響更加敏感。

定義的變精度粗糙集上近似集為：

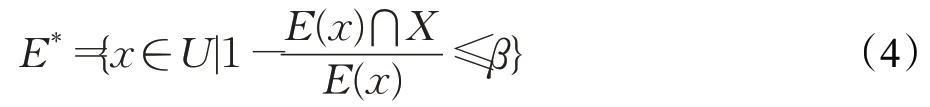
其中，β表示閾值時所求上近似集是嚴格的，當β=1 則會將所有的x納入上近似集。所以β越小，最終的結果越有意義。

2 強化依賴度的分析方法

存在這樣的情況，在引入變精度粗糙集的情況下，當β ＜1 時，β的任何變化不會引起上近似集的改變，其原因可能是多個依賴度過低的次要屬性存在于決策表中。

由于屬性依賴度對于各屬性之間的依賴關系有重要意義[20]，通過強化屬性依賴度放大屬性之間的依賴關系，挖掘次要屬性。

強化屬性依賴度過程如圖1所示，計算不同的條件屬性Ac之間的組合依賴度，再將屬性組合的依賴度先從組合分離，后合并于每個屬性，使得重要屬性與次要屬性分開，給出每個Ac關于Ad的依賴度，其中依賴度的強化主要體現在合并操作上。

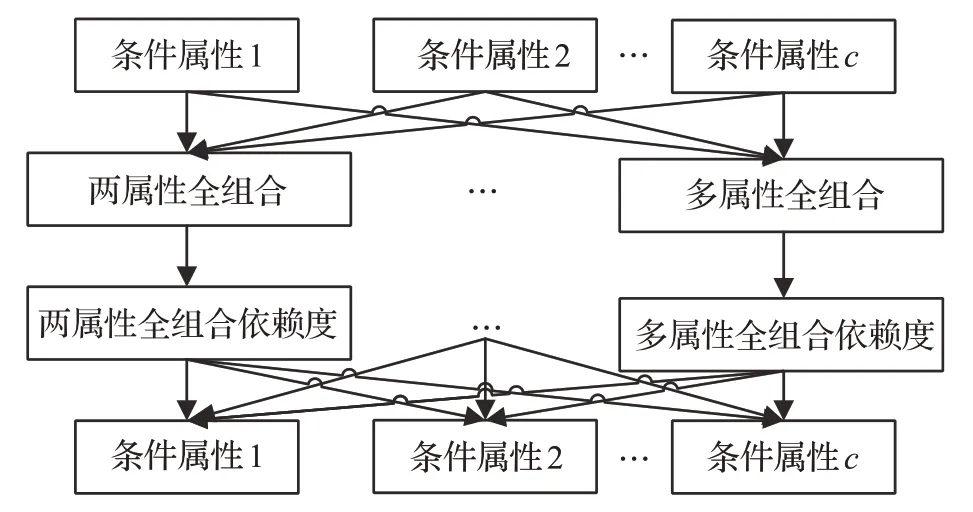
圖1 依賴度分離合并示意圖

屬性全組合方式為式（5），其中g表示組合的元素數，即對g個屬性進行組合，記組合總數為m1,m2,…,mj，j為組合類型數。

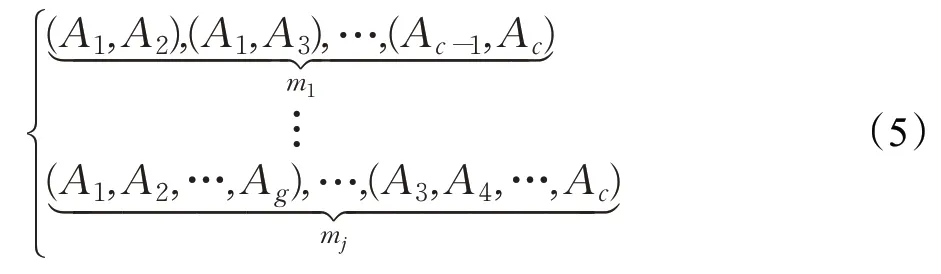
則可得對應的決策矩陣可為：

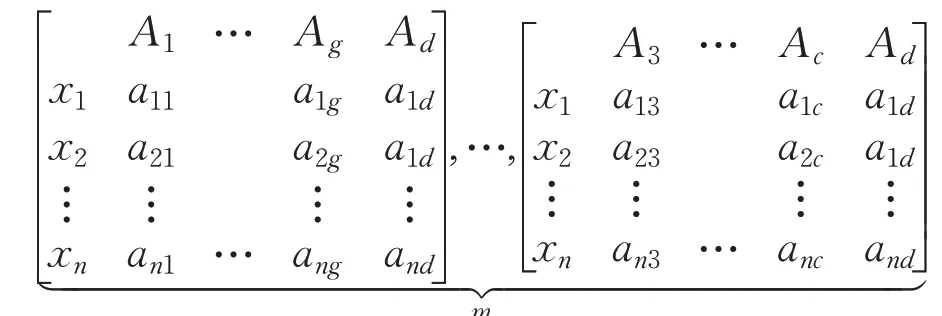
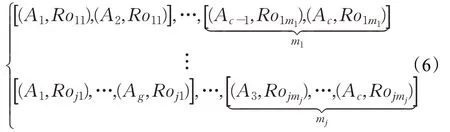
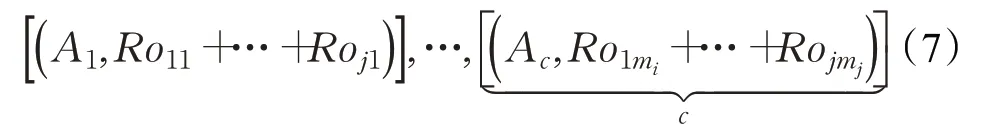
2.1 多粒度粗糙集與數據離散化方法

各屬性組合進行計算較好地保留了屬性之間的關系特點，但求解上近似集的過程中直接參與運算的是屬性值，該模型數據的離散化對結果的影響很大，處理結果必須最大程度保留數據特點。強化屬性依賴度過程中，考慮多個數據粒度可更大程度保留數據特點，粒計算是數據挖掘中的一個重點，相較于單粒度，多粒度視角的粗糙集對數據分析更全面、視角更廣泛，通過融合多粒層的結果求得復雜問題的最終解[21-23]。

從不同粒度層面分析數據將更大程度地保留數據的特點，離散化數據時粒度與離散量成反比，若數據離散量越大，則粒度越小，反之越大。通過規定不同的離散量將數據離散化，待處理屬性值其中δ為離散量，不同的離散量對應不同的粒度。

常見的離散化方法有等寬、聚類等[9]，地震相關數據涉及面廣，不同屬性的數據特點不同，根據不同類型的數據使用不同離散化方法，針對本文數據給出判斷公式，對量級差距大的數據進行動態的離散化。

根據離散量，處理不同類型數據的相對距離的流程如圖2所示。

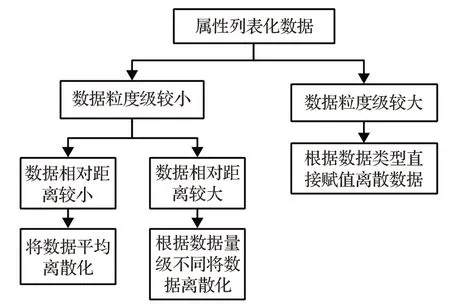
圖2 對不同特點的數據進行離散化

數據粒度較大時數據本身已有歸類與聚集，不做處理；數據粒度較小時，判斷數據的相對距離后將數據離散化處理。為判斷數據粒度大小，在2.2節給出探索模型。

根據式（8）判斷數據的相對距離。

2.2 探索模型

在強化依賴度的數據挖掘模型中，屬性全組合與不明確的粒度范圍將增加方法的復雜度。為確定多個粒度的范圍及每個粒度的粒化準則，去除無效的組合方式，提出一種離散量與屬性組合探索模型，其中粒化準則確定了離散量，粒度范圍為離散量范圍。

確定待處理數據的結構，建立大量與其結構相同的隨機矩陣，通過計算平均依賴度，觀測依賴度變化與離散量及屬性組合的關系。為使隨機數處理更接近待測數據，建立模型的流程如圖3所示。

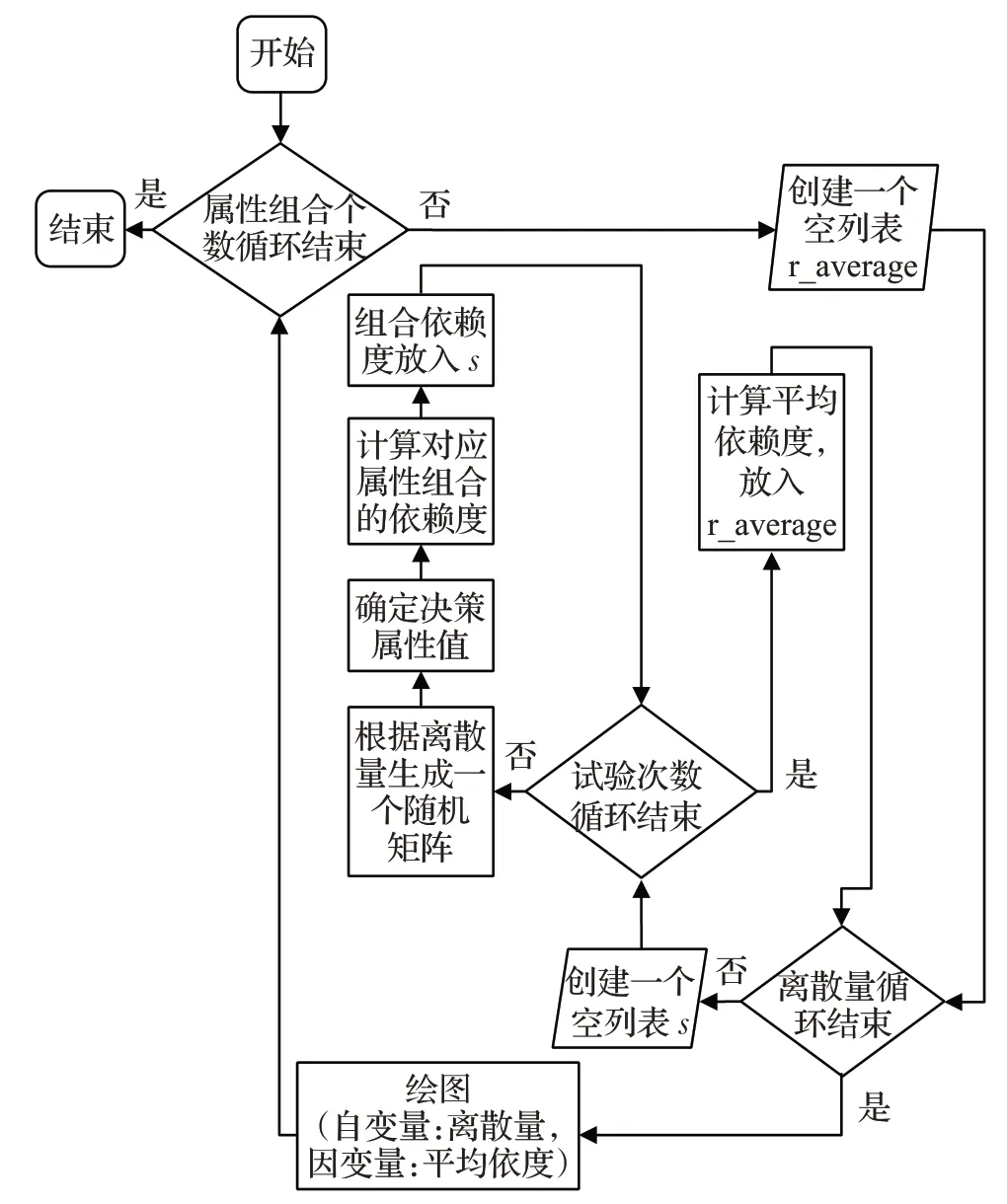
圖3 探索模型程序流程

2.2.1 數據隨機

在對隨機矩陣的屬性進行隨機數賦值時，根據離散量δ產生隨機數如式（9）：

式（9）中，anc為屬性值。此處數據隨機的結果與待測數據的離散化形式一致，在一定程度上模擬了待測矩陣離散化后的數據結構。

2.2.2 屬性組合隨機

在使用待測數據進行計算時，各屬性數據具有對應情景的數據特點，而探索模型中根據離散量產生的隨機數據，數據特點一致，在測試屬性組合數時不需考慮全組合情況，組合結果滿足式（10）：

對比依賴度分析方法中的全屬性組合，合理的離散量范圍與屬性組合范圍取決于決策矩陣本身的結構，而不是屬性間的關系，因而此處組合結果更簡單，且能達到探索模型的目的。

2.3 數據挖掘模型流程

融合上述方法為本文數據挖掘模型，如圖4 所示，依賴度過低的屬性過多，不易從決策矩陣中挖掘，提出依賴度強化方法。引入多粒度粗糙集對數據預處理，動態的離散化數據，從多個角度提取數據特征；使用探索模型給出離散量范圍與屬性組合范圍，將數據預處理進一步合理化。

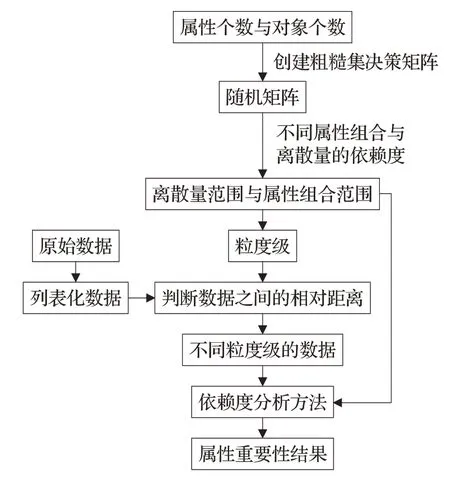
圖4 數據挖掘模型

探索模型與多粒度視角處理數據均是為了提高依賴度分析方法的合理性。

3 實驗和分析

3.1 數據集

選取國內18 次地震作為研究樣本，用以驗證該方法的合理性、實用性。通過對以往地震案例的研究歸納明確了在應急預案中的幾個重要影響因素。

首先確定影響因素有：人口密度、當地氣候類型、季節、時間、往年地震情況、地震等級、當地地形。往年地震情況為當地或者當地對應省、市近50年內震級5級以上的年均地震次數。將經濟損失作為決策屬性，其他影響因素作為條件屬性，原始數據如表1。

3.2 對比實驗改進的屬性約簡數據挖掘模型

3.2.1 探索離散量與屬性組合范圍

根據探索模型，確定實驗數據中對象個數為18，條件屬性為7，決策屬性為1，在實驗中給出最小的離散量為3。根據粒度與屬性組合探索模型得出屬性依賴度變化圖，如圖5所示。

圖5 中曲線的自變量有兩個，為粒度與屬性組合。橫坐標為自變量粒度，第一個粒度離散量為2，因實驗發現粒度過大無意義，省去，從第二個粒度開始，實驗中從第七個粒度開始依賴度隨兩個自變量的影響變小，自變量粒度選取第二至第七個，粒度Attribute granularity與離散量δ的關系：Attribute granularity=δ-1；各連續的曲線為自變量屬性組合，實驗選取全部屬性組合。因變量為平均屬性依賴度，即每個屬性粒度對應不同屬性組合所得平均屬性依賴度，圖5由500個隨機8×18屬性矩陣計算平均值得出。根據圖5中5、6、7三種屬性組合在本實驗中明顯聚集，區分能力較弱，首先去掉這三種組合，故均用實線表示。

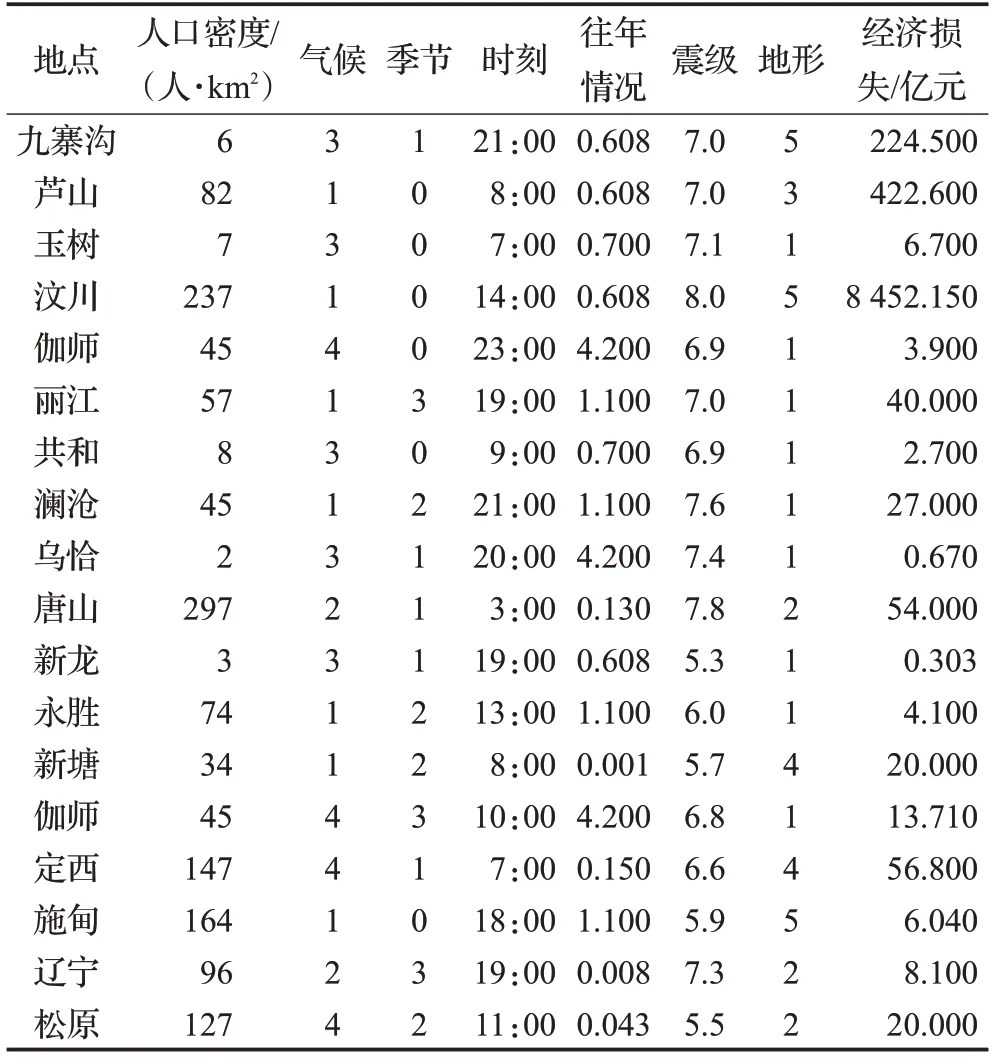
表1 地震經濟損失及其影響因素

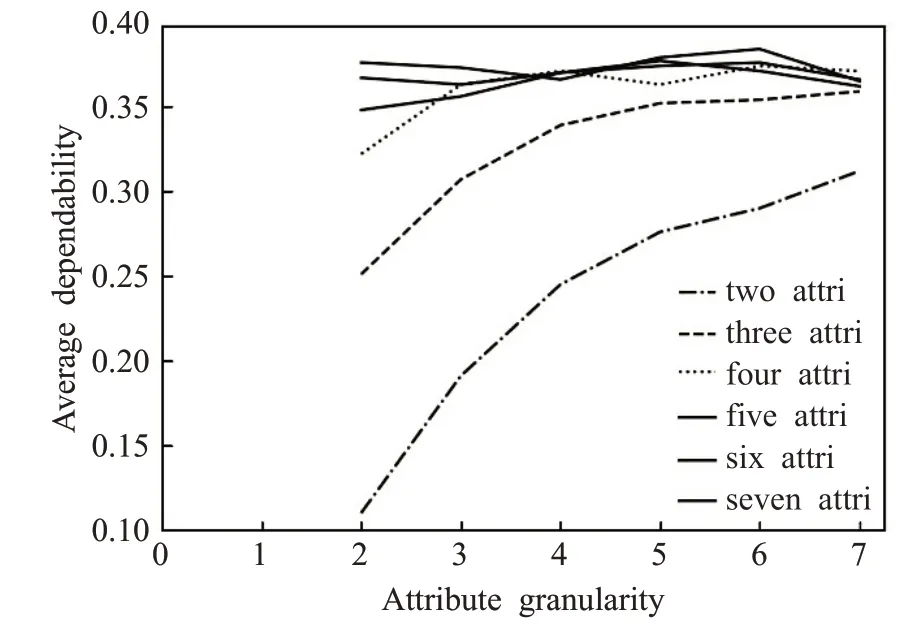
圖5 依賴度隨粒度與屬性組合的變化

分析圖5可知，當決策屬性個數為1，條件屬性個數為7，屬性對象為18個時：在每個粒度層面，隨屬性組合個數的減少，屬性依賴度差距變大，屬性依賴度關于粒度變化的斜率變大。根據屬性依賴度的差值與斜率挑選粒度與屬性組合范圍。選取差距較明顯、斜率較大的情況，屬性之間的依賴度差異較大，最有可能分離出重要屬性與次重要屬性。

3.2.2 數據處理

經濟損失數據受年代影響較大，為消除這種經濟發展變化造成的對比不均等現象，將經濟損失與當年GDP的比值作為決策屬性值。

挑選具有一定代表性的數據直方圖，第一類數據如圖6所示。

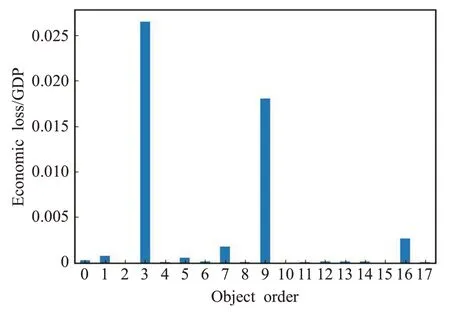
圖6 決策屬性的數據直方圖

圖6決策屬性為經濟損失與當年GDP的比值，自變量0 至17 代表18 個實驗對象。此類數據為第一類數據，內部量級相差較大，且存在多個數據量級，根據本文離散化方法，需要采用不同的τ；第二類數據，如往年地震情況中有較明顯的聚集情況，設置其τ為1.25，而經濟損失的τ為2；第三類數據，如時間、地震等級，其數據內相對距離較均勻，將其平均離散化；第四類數據，如氣候、地形，此類數據本身較為離散，它們之間關系較不明確，直接賦離散值。

取部分結果舉例，離散量為3的數據處理結果如表2 所示。對應決策表定義，表2 中a1至a8表示屬性，對象p1至p18表示震發地點。

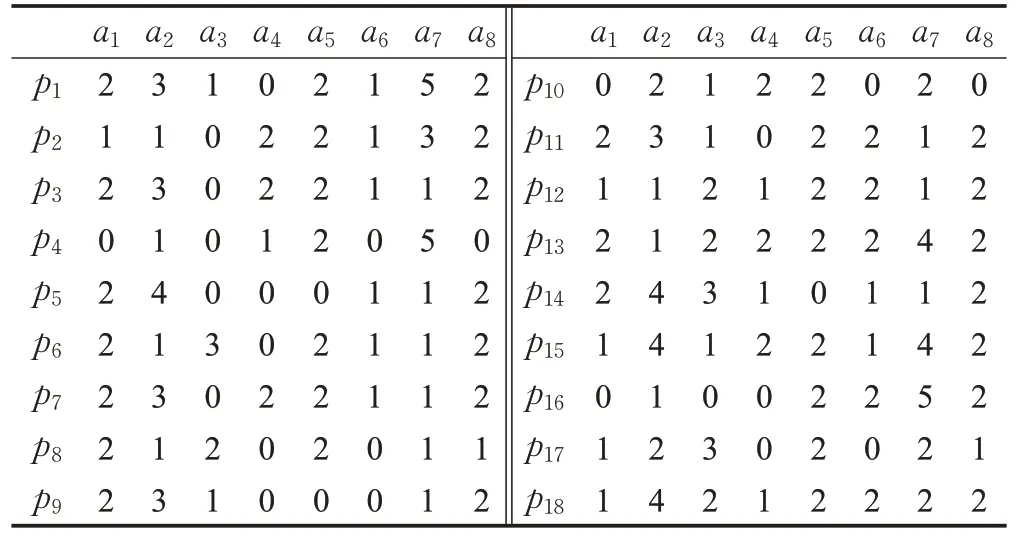
表2 部分處理后數據

在傳統聚類方法中，如圖6中的數據離散將會分離3 號、9 號地區，動態離散化方法中，當離散量為3 時，3號、9 號地區將不會分離，符合二者同屬于大型損失的情況。

3.3 實驗結果

3.3.1 依賴度強化方法

決策屬性a8的值0、1、2 分別對應大、中、小三種程度的經濟損失。離散量為3、4、5，屬性組合為2、3、4，決策屬性值為0、1、2的屬性組合依賴度結果如表3。

表3 屬性在組合中的依賴度

經統計，表3共得出546個依賴度結果，包括針對三種決策屬性的結果，每種結果包括三種粒度，將三種粒度的結果累加。

根據決策屬性不同，合并依賴度結果如表4。

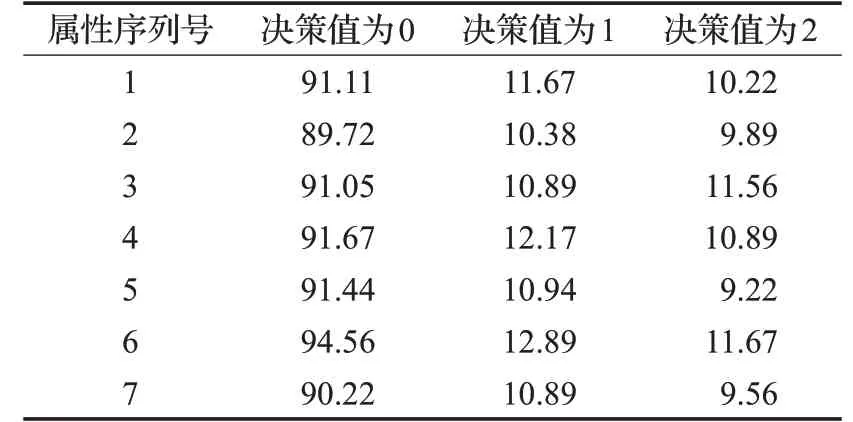
表4 每個屬性的依賴度累加值

根據表4 屬性依賴度結果大小將其對應屬性序列號排序如表5。

表5 屬性序列號從大到小排序

表5 中屬性序列號依次對應7 個條件屬性，條件屬性對應到影響因素，屬性重要程度排序如表6。從表6中可以得出，三種決策屬性互為測試集，且三種排序結果較接近，體現出該模型的合理性。根據排序結果可看出，地震等級與時間在決策中較為重要，地形與氣候較不重要。

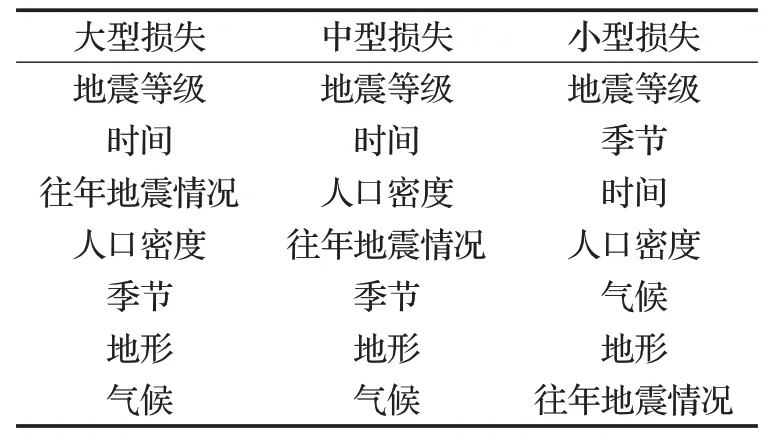
表6 影響因素的重要度從高到低排序結果

3.3.2 傳統屬性約簡方法

為證明本文方法的必要性，使用同樣數據，通過傳統的屬性約簡方法計算，結果如表7。

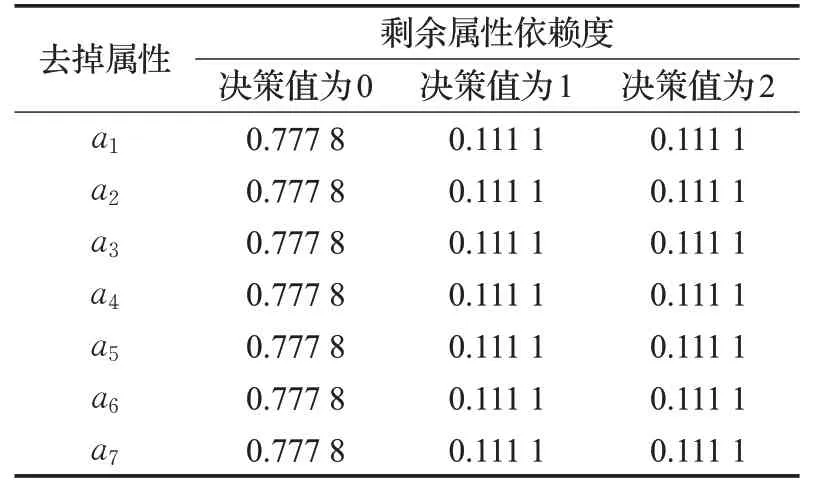
表7 傳統屬性約簡依賴度結果

根據表7，每一列的依賴度結果均沒有變化，根據變精度粗糙集理論進行計算，當β為0.9時結果仍不變，表示通過傳統的屬性約簡無法挑出約簡的刪除對象。

3.3.3 測試數據結果

為證明本文方法的合理性，表8選取了50個較為傳統的隨機決策矩陣作為測試數據。

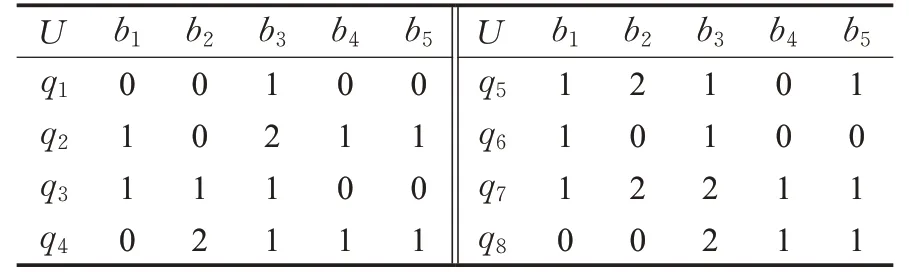
表8 測試數據1

該決策矩陣中有5個屬性，8個對象q1～q8，離散量為3，決策屬性b5，條件屬性b1～b4。

首先使用本文方法，統計依賴度結果如表9。再使用傳統屬性約簡方法，引入變精度粗糙集，取β為0.3（實驗得：不使用變精度粗糙集時，存在兩個屬性的依賴度在約簡過程中恒為0；且β取0.1、0.2均無變化），結果如表10。

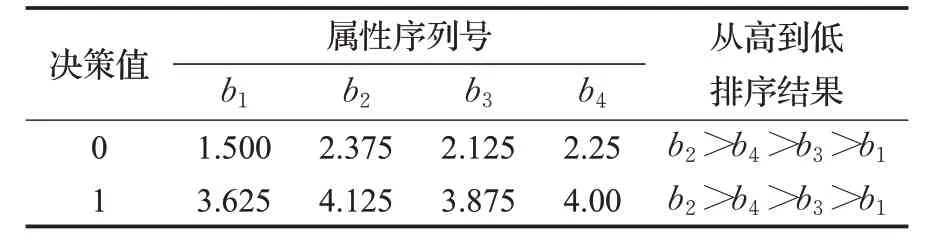
表9 強化粗糙集屬性依賴度的數據挖掘方法結果

根據表10 的屬性約簡結果可得，使用傳統的粗糙集屬性約簡理論時，條件屬性依賴度值的大小排名為：b2＞b4＞b3＞b1。對比表9 的結果，則該測試數據中本文方法與傳統方法的表現結果一致。

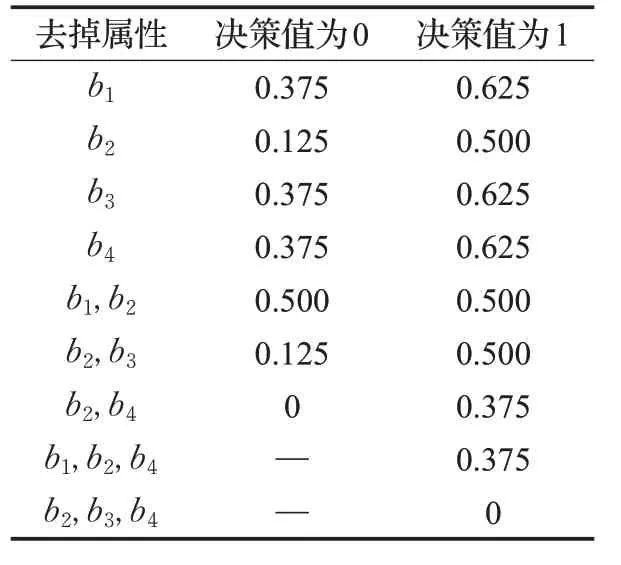
表10 傳統屬性約簡結果

實驗證明，兩方法在50 個測試數據中有43 個表現結果一致，一致性為86%，故本文方法具有一定的合理性。

4 結束語

對于傳統的屬性約簡方法中存在的過多低依賴度屬性、過小粒度級導致的約簡困難現象，本文以強化依賴度為主要思想，提出一種依賴度分析方法并構建了數據挖掘模型。在模型中，引入多粒度粗糙集，針對本文數據集給出了一種數據離散化方法，更大程度地保留了屬性特點；構建探索模型，給出了一種粒度準則確定方法，合理縮小了屬性組合范圍與離散量范圍，減少過量的計算；在選取決策屬性時，從經濟損失結果出發考慮了不同等級的經濟損失程度。該模型綜合考慮了不同屬性組合的關系；從不同粒度層面分析了數據，成功挖掘出較重要屬性與較次要屬性。在實驗數據中本文模型表現較好，在測試數據中本文模型與傳統模型結果一致性較高，體現了本文數據挖掘模型的必要性與合理性。本文數據量較小，有待研究更多屬性情況或其他領域下模型的合理性與魯棒性，在更廣泛領域的數據挖掘中有待進一步研究。