高中信息技術課程Python教學項目的設計
任赟
2017年春季學期,北京作為全國四個試點省份之一開始實施新課標。2018年1月《普通高中信息技術課程標準(2017年版)》發布,前言中提到要“落實立德樹人根本任務,……培養德智體美全面發展的社會主義建設者和接班人”。在新課標中,教學內容以程序設計語言Python作為載體,培養學生信息意識、計算思維、數字化學習與創新、信息社會責任四個核心素養。
2020年的新冠肺炎疫情對全世界各行各業都產生了深遠的影響。高一學生作為未來社會主義的建設者和接班人,為了更好地幫助他們了解新冠肺炎的相關知識,了解我國采取各種疫情防控措施的必要性,進一步產生國家自豪感、認同感,筆者設計了與新冠肺炎相關的兩個教學項目。
這兩個項目立足于立德樹人基本思想,同時也有利于培養學生的信息技術課程的四個核心素養。
項目一:新冠肺炎自查程序
1.設置目的
(1)幫助學生了解新冠肺炎與普通感冒的區別。
(2)幫助學生綜合運用Python中的if條件語句。
2.項目描述
在新冠肺炎疫情期間,普通人如果出現發熱、咳嗽、流鼻涕等癥狀,但無法確認病情,又擔心去醫院會出現交叉感染,怎么辦?
請使用Python制作一個小程序,通過詢問用戶問題,幫用戶初步識別患新冠肺炎的概率,并給出相應的建議。
3.具體要求
(1)請從網上查詢并整理資料,了解普通感冒和新冠的區別。
(2)使用Python完成一個小程序,通過詢問用戶問題,幫用戶初步識別患新冠肺炎的概率,并給出相應的建議。
4.項目范例
(1)程序功能說明。
詢問用戶以下四個問題:
①是否有呼吸困難或急促?
②是否有干咳并影響睡眠?
③是否持續發熱且退燒藥作用不大?
④是否精神差、食欲差?
輸出用戶感染概率
規則如下:用戶四個回答中,每個“是”回答感染概率增加25%,根據用戶回答“是”的數量給出感染概率。如用戶回答0個“是”,感染概率為0%,1個“是”,感染概率為25%,依次類推。
根據用戶感染概率給出相應建議:
①0,您目前很正常,請出門戴口罩,勤洗手,做好個人防護。
②25%~75%,您有一定的感染概率,請做好自我隔離,必要時去醫院就診。
③100%,您的感染概率非常大,請帶好口罩,立即去醫院就診!
(2)參考程序(Python語言版)。
p=0#感染概率
ans=input('1.是否有呼吸困難或急促(回答是或否)')
if ans=='是':
p+=25
ans=input('2.是否有干咳并影響睡眠?(回答是或否)')
if ans=='是':
p+=25
ans=input('3.是否持續發熱且退燒藥作用不大?(回答是或否)')
if ans=='是':
p+=25
ans=input('4.是否精神差食欲差?(回答是或否)')
if ans=='是':
p+=25
print('您的感染概率為',p,'%')
if p==0:
print('您目前很正常,請出門戴口罩,勤洗手,做好個人防護')
if 25<=p<=75:
print('您有一定的感染概率,請做好自我隔離,必要時去醫院就診')
if p==100:
print('您的感染概率非常大,請帶好口罩,及時去醫院就診')
項目二:傳染病數學模型下的疫情變化
1.設置目的
(1)幫助學生了解在不進行隔離的情況下,傳染人數的快速增加,從而幫助他們更好地理解國家的隔離措施實施的必要性。
(2)幫助學生培養使用程序解決現實問題的意識。
(3)幫助學生對Python程序設計語言中的順序結構、循環結構進行綜合練習。
2.項目背景
當一種傳染病(如SARS、新冠肺炎等)正在流行,人們希望建立適當的數學模型,利用已經掌握的一些數據資料對該傳染病進行有效的研究,以期對其傳播蔓延進行必要的控制,減少人民生命財產的損失。常見的傳染病模型按照傳染病類型分為SI、SIR、SIRS、SEIR 模型等。
傳染病模型一般把傳染病流行范圍內的人群分成如下幾類。
(1)S類,易感者 (Susceptible),指未得病者,但缺乏免疫能力,與感染者接觸后容易受到感染。
(2)I類,感染者 (Infectious),指染上傳染病的人,可以傳播給S類成員,將其變為E類或I 類成員。
(3)R類,康復者 (Recovered),指被隔離或因病愈而具有免疫力的人。如免疫期有限,R 類成員可以重新變為 S 類。
(4)E類,暴露者 (Exposed),指接觸過感染者,但暫無能力傳染給其他人的人,對潛伏期長的傳染病適用。
為了簡化問題,本項目使用SIR模型。
有兩個假設:
①地區總人數N不變,沒有人生死遷移,只有健康者S(t),感染者I(t),康復者R(t)。
備注:S(t)表示第t天的健康者,I(t)表示第t天的感染者,R(t)表示第t天的康復者。
②疾病傳染率為β,每天治愈率為γ。
SIR模型(不進行隔離)如下:
①S(t)+I(t)+R(t)=N
②?S(t)=β*I(t)*S(t)/N(第t天新傳染的人數,即第t天健康者減少的人數)
③?R(t)=γ*I(t) (第t天康復者增加的人數)
④?I(t)=β*I(t)*S(t)/N-γ*I(t) =?S(t)- ?R(t) (第t天現存感病者增加的人數)
3.具體任務
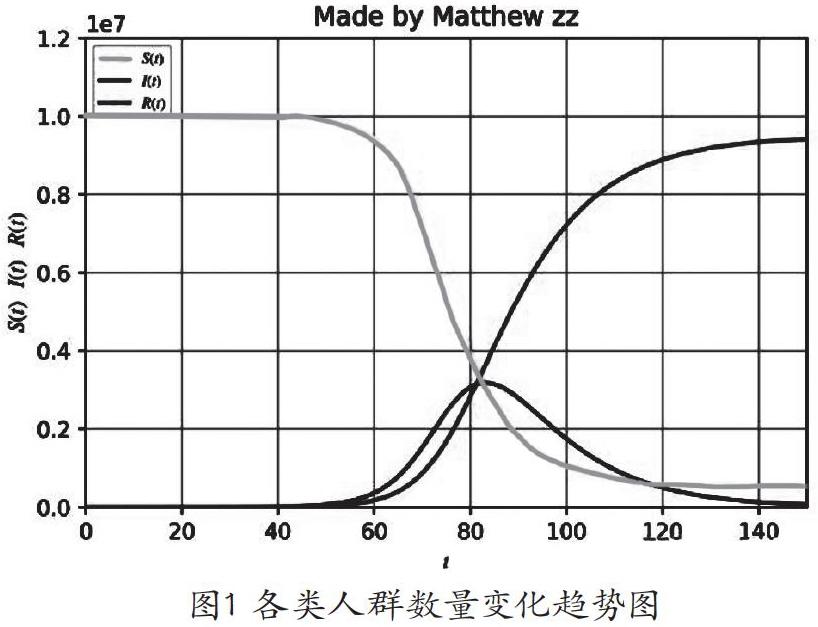
假設傳染率β取值0.2586,治愈率γ取值0.0821,S0、I0、R0的初值分別是10 000 000、10、5,則N=10000000+10+5,人數變化趨勢如圖1所示。
請計算:
任務1
第一天,健康者S、感染者I、康復者R各有多少人數。
任務2
輸入天數,計算該天健康者S、感染者I、康復者R的人數。
任務3
計算拐點出現的天數(從拐點開始新感染人數小于康復人數,即總感染人數開始減少)。
4.參考程序
結? 語
以上兩個項目既可以幫助學生了解疫情的相關知識,又可以幫助學生對Python進行綜合練習,受到學生們的喜歡。我們的學生是未來社會的建設者,建設者的技能不是一蹴而就的,需要教師的持續引導,引導他們關心社會,思考社會問題的解決方法,這樣在未來他們才能理論聯系實際,學以致用,成為合格的建設者和接班人。
作者單位:北京市第十二中學

