實踐活動中數學思維的培養策略

薛正檜

培養學生數學思維能力是一個持續、漸進的過程，它不是原始素材的簡單堆砌，而是相關要素的逐層遞進。教學活動有的放矢，學生的思維才能逐級提升。用三角板畫角原本只是“角的認識”課中的一道習題：“你能用三角尺畫出15°、150°、165°、75°嗎？”這道題在幫助學生加深對三角板認識的同時，可以有效地提升學生的思維能力，教學價值極其豐富。我們將其開發成一節實踐活動課，意在為教師尋找培養學生數學思維的路徑提供一種參考。

一、從思考到操作

數學是研究數量關系和空間形式的科學，是思維的體操，從內容的表現形式看，通常分三個層次，即形象、表象、抽象。數學最核心、最本質的內容必定是抽象的，它脫離現實，是關于符號的知識體系。但兒童最能理解的數學卻是形象的，這和他們的思維水平有很大的關系。教育的目的是培養人，“基于兒童”之后更要“發展兒童”，生活化、兒童化只是學習的橋梁，最終必須數學化。當我們面對問題時，不要急于解決問題，先靜下心來想一想，抽象有困難再去結合表象，表象有困難再去結合形象，千萬不能一直從低階開始。實踐證明，長期在直觀、形象、操作的層面解題，學生的思維就有了惰性，此時再想發展思維能力就更難了。

實踐活動“用三角板畫角”一課，我們可以按下面的步驟展開教學。1.情境感知：三角板中各有哪幾個角？分別多少度？2.提出問題：用三角板可以畫出哪些不超過180°的角？3.選擇策略：你準備怎么解決這個問題？4.初步設想：你已經想到了哪些角？這些角分別是怎么得到的？5.啟發思考：還會有其他不一樣的角嗎？6.操作驗證：請拼出剛才說的這些角。7.思維頓悟：活動中你又發現了哪些不一樣的角？8.反思質疑：拼角、畫角的過程讓你想到了什么？你有哪些收獲？在上述教學設計中，操作的作用是驗證、鞏固，以及思考無助后的靈感觸發。這樣的課堂，有濃濃的數學味，學生能學到真正的數學。

二、從嘗試到聯想

從熟知的事物及現象中發現規律，然后通過驗證得出結論，是人們獲取知識的一般路徑。在這條路徑下，兒童的觀察、猜想、實驗、推理、概括等能力得到了有效的訓練與提升。小學生喜歡在熟悉的領域內按熟悉的方式進行學習，這是他們這個年齡段應有的狀態。從實例中獲取知識是一種方式，從已有結論中二次獲取知識也是一種方式。數學可以來源于生活現實，也可以來源于數學現實。聯想就是一種有效的學習方式。在聯想中，學生的思維處于一種發散狀態，思維的靈活性、深刻性、敏捷性、創造性等品質都會得到發展。

在“用三角板畫角”一課中，我們可以在以下幾個方面引導學生展開聯想，從熟悉到陌生，有梯度地培養他們的思維能力。第一，運算上的聯想。把兩個角相加得到新角是學生熟悉的，但把兩個角相減得到新角則是學生陌生的。如圖1，45°角和30°角合并拼，可以得到75°角，如果將它們部分重疊起來拼，又會得到多少度的角呢？

第二，空間上的聯想。在三角板內部拼角是學生熟悉的，但從三角板外部找角則是學生陌生的。如圖2，借助一條直線，在兩塊三角板外，又能得到多少度的角呢？

第三，數量上的聯想。利用兩個角畫角是學生熟悉的，但利用三個角或者更多的角畫角則是學生陌生的。如圖3，在已有75°角（45°+30°）的外延再增加一個90°角，又能得到多少度的角呢？

這樣的課堂靈動而富有張力，教師一兩句的引導、點撥，便能給學生打開一扇知識的窗口。

三、從零散到系統

有效的學習要體現在對某個知識點的理解與掌握上，也要體現在對既有認知系統的擴充或重組上。零散的知識點只有經過系統化后，才能內化為學生的所得。一方面，零散的知識記憶起來麻煩，而且很容易忘記;另一方面，零散的知識沒有形成體系，容易導致思考問題片面。在教學中，教師要注重溝通新舊知識的聯系，注重多角度、多維度地呈現知識，幫助學生把零散的知識組成系統，逐步建立完整的知識結構。在系統化過程中學生的思維更加有條理，這將有利于他們準確地闡述自己的思想和觀點，有利于他們運用數學概念、思想和方法，形成良好的思維品質。

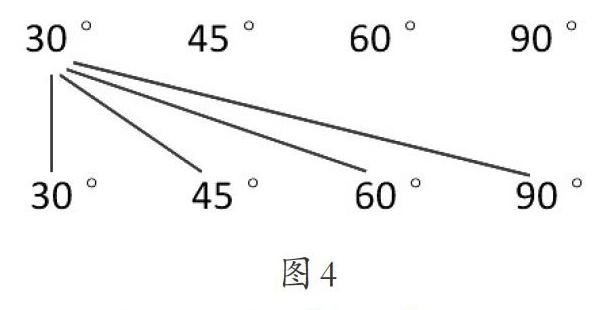
在“用三角板畫角”一課中，我們至少可以從以下兩個方面引導學生對零散知識進行系統化整合。一是與“搭配（排列組合）”連接。用三角板畫角，換個思路看，其實就是對三角板中已有的角度（30°、45°、60°、90°）進行自由組合。按圖4的方式，先兩兩連線得到16種組合，再分別進行加減運算得出32個度數，最后剔除相同的答案。在此基礎上，為了得到更多的角度，還可以將剛剛得到的度數再與原有的4個度數組合。

二是與“找規律（等差數列）”連接。在學生嘗試以后，可以讓他們將初步得出的角按順序排列起來（15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°、180°）。此時學生得出的角可能不全，這很正常，不用刻意補充。教師只須引導他們觀察已有數據，努力發現數值排列的規律。因為有豐富的找規律經驗，他們會很快發現相鄰兩個角之間的度數差大部分是15°或全部是15°。之后，找全的學生會根據“等差”這一特性進行更全面的思考;找不全的學生會自覺補全遺漏度數，并進行嘗試、驗證，最后獲得完整答案。我們還可以從15°的整倍數這個角度引導學生發現、歸納，構建出多維的知識體系。零散的度數有了系統化的理解后，學生的思維必將深入而持久。

（作者單位：浙江省寧波濱海國際合作學校）