灰色冪模型在基坑變形監測中的應用

張 進 彭 磊 尹亞東

(中國電建集團河北省電力勘測設計研究院有限公司, 河北 石家莊 050015)

0 引言

近年來,我國經濟飛速發展,基礎建設速度的加快和施工難度的逐漸增大,對工程安全性的要求也是越來越高,如在地質環境脆弱的地區建設高層建筑物,在地下水密集的地帶開挖隧道,在建筑物密集的城市中心建設地鐵軌道交通使得建筑物產生沉降。在工程運營的整個過程中需要及時預測和準確預報建筑物的形變量和狀態,這不僅對整個工程的施工和管理至關重要,也關系到人民的生命財產安全[1]。

灰色模型可以利用小樣本量和少信息量對不確定的數據來進行預測和擬合,并且由于灰色模型具有簡便和可操作性強的特點,被廣泛應用在多領域的預測和分析中[2]。傳統GM(1,1)模型對于具有非線性特征趨勢的數據沒有較好的預測效果[3]。灰色冪模型NGBM(1,1)是傳統GM(1,1)模型的一種重要改進模型,灰色冪模型是一種可以擬合和預測具有非線性特征數據序列的模型,它可以通過改變自身的參數來適應不同變化趨勢的數據類型[4]。由于灰色冪模型是GM(1,1)模型的拓展形式,所以它具有灰色模型的性質,可以用“小樣本”和“貧信息”的數據來進行預測,此外還在一定程度上擴大了灰色模型的適用范圍和精度。本文將灰色冪模型應用在基坑監測預報中,并對應用過程進行分析,與傳統模型進行對比。

1 灰色模型的建立

首先,是對原始數據序列進行累加,從第二項開始累加,新的序列的每個值是原始序列的第一個值到新的序列所對應的值的累加所得,假設非負的原始數據序列為:

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

那么X(0)的一次累加生成序列為:

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

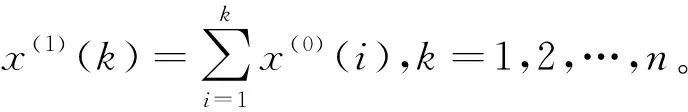
然后,根據一次累加序列求出背景值序列,背景值生成是在求解灰色模型時,以每相鄰的兩個一次累加序列值取平均值或取兩個一次累加值中間的某一值,假設Z(1)為X(1)緊鄰均值生成序列:Z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),其中,

z(k)=px(1)(k)+(1-p)x(1)(k-1),
k=2,3,…,n

(1)

p取0到1之間的任意一值,一般情況下取p=0.5,其中Z(1)稱為背景值。

利用累加序列和背景值序列構建如下方程:

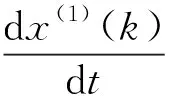
(2)

稱式(2)為GM(1,1)模型。

2 灰色冪模型

在已經得到的灰色GM(1,1)模型作用量b后乘背景值的γ次方,即(z(1)(k))γ,其中γ≠1,得到具有非線性特征的灰色冪模型NGBM(1,1):

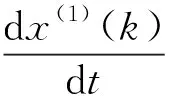
(3)

式中,γ為冪指數,可以根據不同的變形監測數據來調整冪指數γ,使預測的精度達到最優。其中,GM(1,1)模型為NGBM(1,1)模型在γ=0時的形式。

灰色冪模型NGBM(1,1)的白化方程的解為:

(4)

它的解變為:

(5)

設X(0),X(1),Z(1)如上所述,建立矩陣:

將式(5)化簡成下式:

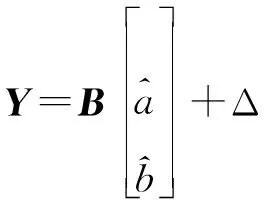
(6)

(7)

最后,用累加生成的序列和均值序列進行計算后,需要對求解灰色模型得到的新序列進行處理,得到其擬合和預測的數據序列,對累加生成的序列進行逆運算,即累減生成:

(8)

冪指數γ可以根據式(4)進行迭代求解,除此之外,用優化算法也可以求解冪指數值,優化算法中比較常見的有:PSO算法、蟻群算法和遺傳算法等,利用這些算法對求解過程優化,以此得到最佳冪指數值。

3 精度評定

對灰色冪模型的預測和擬合的精度檢驗應該使用殘差檢驗、后驗差檢驗這兩種方法。殘差檢驗是對每個擬合值和預測值與原始值求差得出結果,一般用其平均值來評價整體的擬合預測效果;后驗差檢驗是根據殘差概率統計方面的特性來對預測和擬合的結果進行評價。

3.1 殘差檢驗

假設原始的數據序列為:

x(0)=(x(0)(1),x(0)(2),…x(0)(n))

用灰色冪模型進行計算得到的擬合數據序列為:

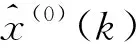
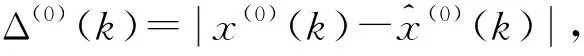
(9)

每個擬合值的相對誤差為:

(10)

用其相對誤差的平均值來評價整體的精度:

(11)

3.2 后驗差檢驗

假設原始的數據序列為:

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))

它與真實值的殘差序列為:

Δ(0)(k),k=1,2,…,n

然后分別計算原始數據序列的平均值和殘差序列的平均值可以分別得到:

(12)

(13)

再根據原始數據序列的平均值計算它的方差可以得到:

(14)

并計算殘差值的方差:

(15)

計算兩者之間的比值,得到式(16),稱其為后驗差:

(16)

根據殘差值和其方差分布規律,計算得到其小誤差概率:

(17)

根據C值和P值的大小對模型的擬合精度進行評定:

當P>0.95,C<0.35時,擬合的精度為一級(優);

當P>0.8,C<0.5時,擬合的精度為二級(合格);

當P>0.7,C<0.65時,擬合的精度為三級(勉強合格);

當P≤0.7,C≥0.65時,模型擬合的精度為四級(不合格)。

4 工程實例

某工程基坑挖深至墊層底為-9.6 m,基坑周長約600 m,挖深約4.1～7.6 m。在變形監測中,采用獨立的高程系,按二等水準測量的方法,對監測點進行測量,儀器自動記錄觀測數據;觀測結束后把觀測數據輸入至計算機作后處理;使用清華山維高程網嚴密平差程序,在計算機上計算基準點高程值。其中環線閉合差0.4 mm,達到《建筑變形測量規范》(JGJ8-2016)級別二級精度要求。為了驗證灰色冪模型比灰色模型有更高的擬合和預測精度,本文取此工程坡頂沉降監測WY2號點分別用灰色模型和灰色冪模型進行擬合和預測。以基坑坡頂沉降點WY2號點為例,它的沉降數據序列為:

X(0)=[0.22 0.57 0.78 0.89 1.24 1.46 1.63 1.70 1.78 1.99 2.08 2.23 2.38 2.45 2.56 2.62];

不妨取前11項數據,來預測后5項數據。根據已有數據進行求解,用灰色冪模型來對其進行擬合預測,第一步是要根據變形監測數據來求取最佳的冪指數,本文根據前11項數據用等步長試探法求取灰色冪模型的最佳冪指數,以0.01為步長從0到2逐個試探,得到冪指數取值和相對誤差的關系,當相對誤差最小時的冪指數值,即待求冪指數值,相對誤差與冪指數取值的關系如圖1所示。

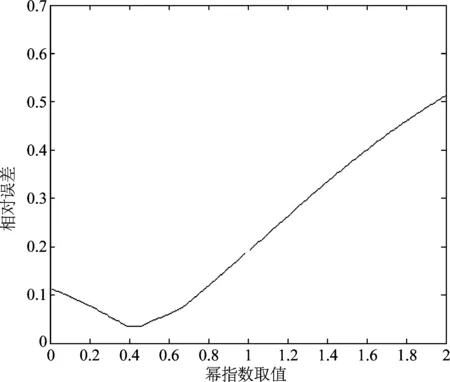
圖1 相對誤差與冪指數取值關系

當冪指數γ=0時,灰色冪模型變為灰色模型。從圖1中可以看出,灰色GM(1,1)模型(冪指數為零時)并非為誤差最小的結果。當相對誤差最小時,冪指數的取值為γ=0.42。

因此,可以得到灰色模型GM(1,1)模型的白化方程參數為:

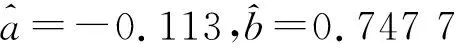
得到灰色冪模型NGBM(1,1),模型白化方程參數為:

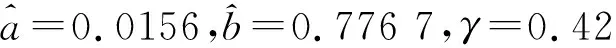
精度檢驗的結果用殘差C和后驗差P來對比。其中,殘差C越小,后驗差P越大說明精度越好。本文將兩種方法擬合和預測的結果繪制成表格和線狀圖,結果如表1所示。

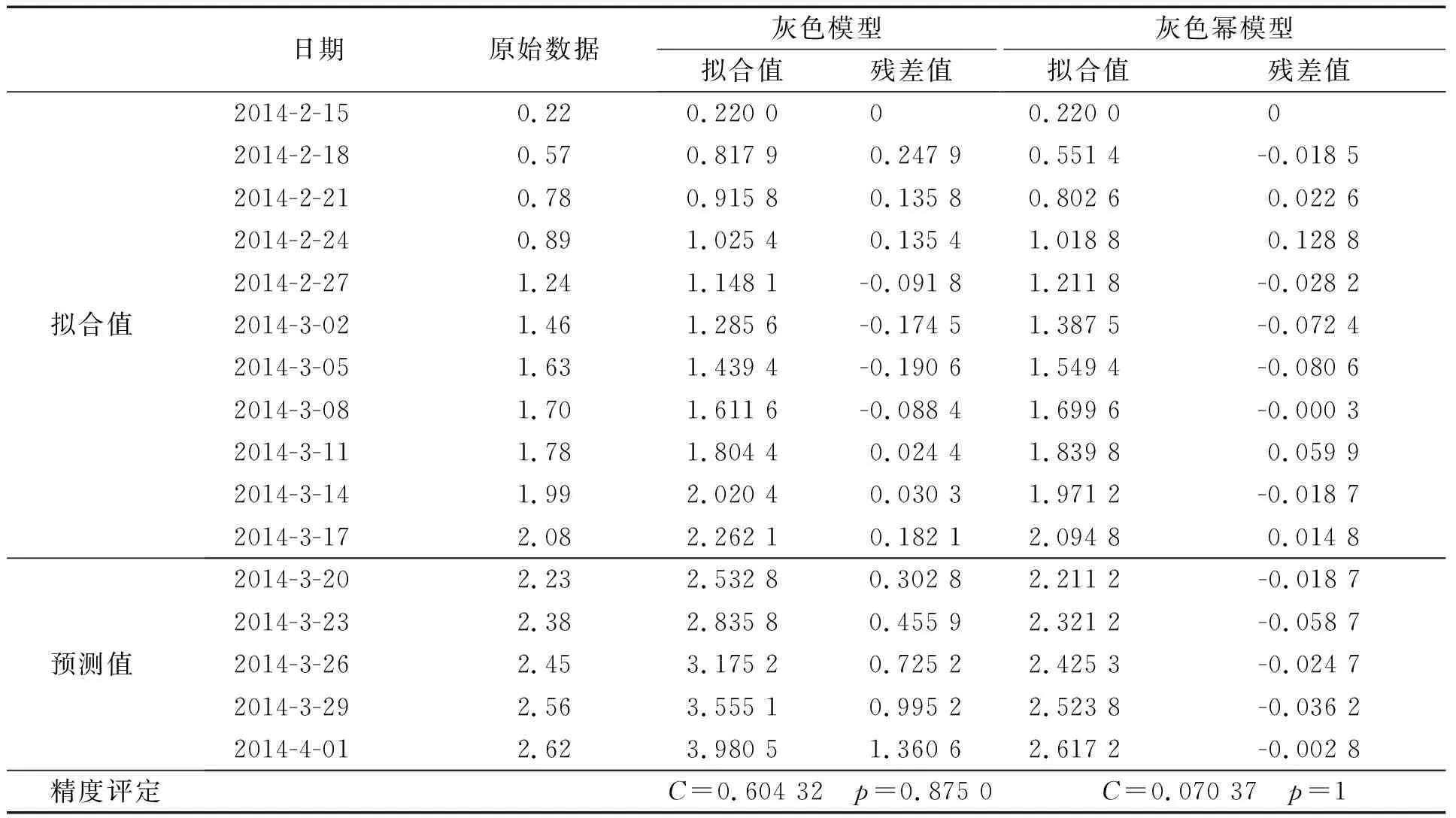
表1 灰色模型和灰色冪模型擬合預測對比(基坑監測點) 單位:mm

將表1中兩種模型擬合預測的結果繪制成線狀圖如圖2所示。

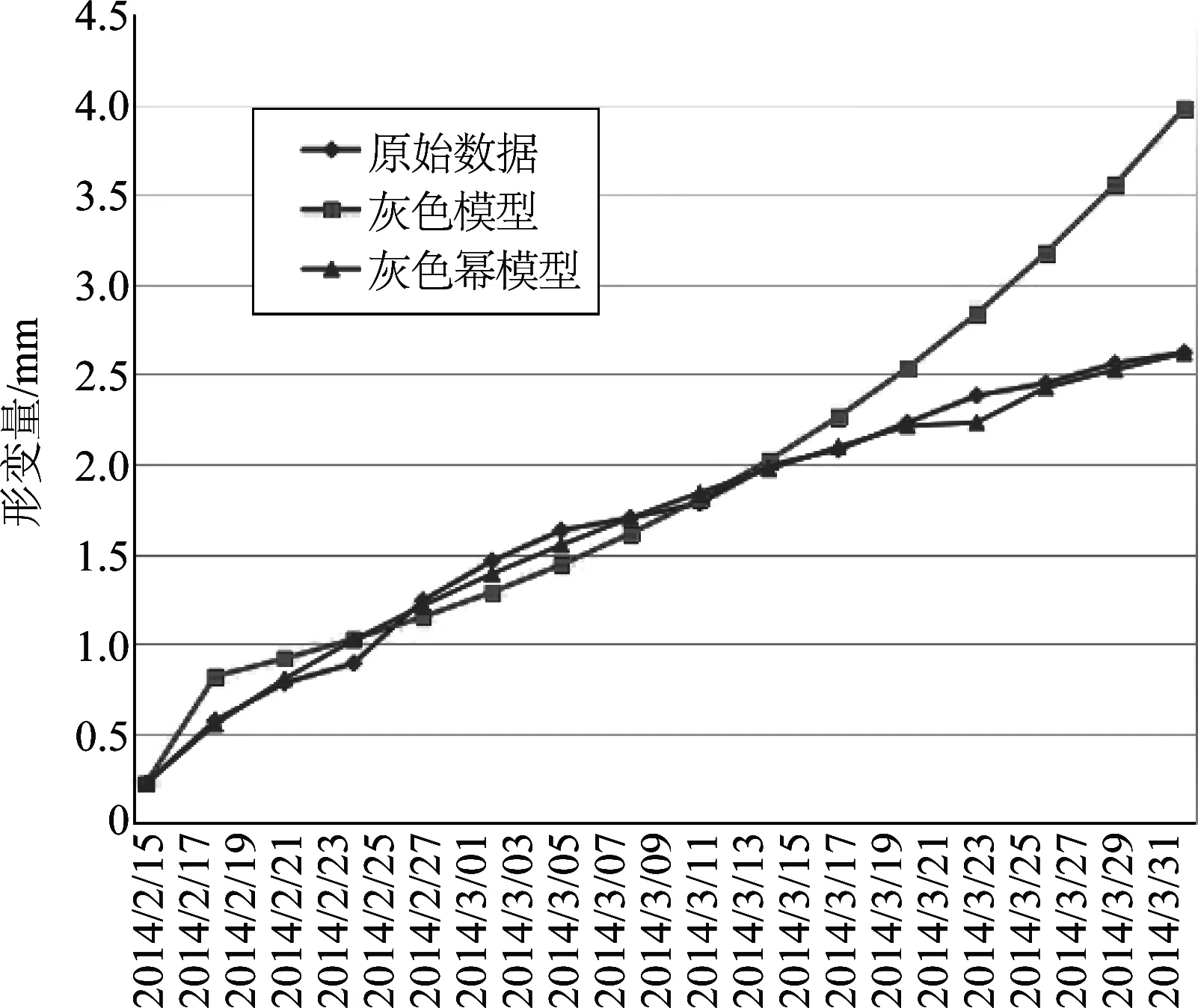
圖2 灰色冪模型與灰色模型擬合預測對比(基坑監測點)

根據結果可以看出,灰色冪模型NGBM(1,1)擬合預測精度比灰色模型高,在變形監測中對非線性特征的數據預測精度比灰色模型有所提高,在基坑監測中的應用比較可靠。

5 結束語

本文在傳統灰色模型GM(1,1)的基礎上,總結了灰色冪模型NGBM(1,1),并對灰色冪模型的參數求解過程進行了說明,結合基坑監測的特點,將其應用在基坑監測預報分析中。通過實驗可以看出,灰色冪模型相較灰色模型在預測精度上有了較大的進步。自從灰色系統理論提出以來,灰色模型得到了較大的發展,多種改進和組合模型被提出,提高了數據擬合和預測的精度,擴大了灰色模型的適用范圍。灰色冪模型這一理論的出現為灰色系統理論又增添了新的內容,豐富了灰色體系統理論體系,灰色冪模型的改進與發展對提高變形監測預報分析的精度有極大的幫助。