基于改進粒子群算法的小麥收割機路徑優化控制研究

祖錫華

（江蘇經貿職業技術學院，江蘇 南京 211168）

小麥收割機已經得到了廣泛應用，其中小麥收割機的作業效率和利用率是保證其完成作業任務的關鍵。但隨著小麥產量的增多，在收割過程中存在的問題越發凸顯。

在每年的收割季節，一些地區的小麥收割機供不應求，甚至還有一些地區的小麥收割機處于閑置狀態，難以取得最佳的收割效率。

目前，對小麥收割機的調度研究還比較少，如果錯過了小麥收割期，麥子將炸開，導致農戶的糧食產量受損。過去，存在中介從小麥種植者和小麥收割機操作工人的聯系中牟利的現象，一方面，使小麥種植者的成本增加，另一方面，使小麥收割機操作工人的收入降低[1-2]。因此，應采取有效的計算對小麥收割機的路徑進行規劃，這不僅能使小麥收割機的成本降低，而且能提高農民的收入。

小麥收割機路徑規劃過程中應依據收割機的路線、位置和速度，通過調度中心對小麥收割機進行合理安排，以保證小麥收割機的調度更加準確和及時。為了確保小麥收割機在不同地區之間的合理資源配置，為其選擇最優路線是關鍵，通過選擇最優的小麥收割機調度路線，能有效降低成本，提高小麥收割機的使用效率，從而提高小麥收割機的經濟效益。目前，人工智能技術與網絡技術正處于不斷發展的階段，農業領域也不斷應用現代技術，能有效提升小麥收割機的工作效率[3]。

為了實現小麥收割機的調度優化，提高小麥收割機的作業效率，將改進粒子群算法應用于小麥收割機調度過程中的路徑優化選擇，能避免傳統優化算法運行效率低和收斂效率差的缺陷。

1 小麥收割機調度路徑優化模型

假設全部的小麥收割機都是相同的類型，根據小麥種植農戶的相關信息確定小麥田的位置以及收割地點，有且僅有一個中心小麥收割機點，不同的收割路線的起點和終點均為中心小麥收割機點。不同的收割路線都處于理想狀態，在構建優化模型過程中忽略了天氣和地勢的影響。

小麥收割機到達時間與小麥種植農戶預約時間偏差的時間窗長短，直接決定了懲罰的成本[4]。假設懲罰成本具有線性特征，當小麥收割機到達時間處于時間窗以內，懲罰成本為0，當小麥收割機到達時間不在時間窗內，懲罰成本根據如下公式計算：

式中：Ci(tig)為小麥收割機g時間ti所對應的懲罰成本；h為小麥收割機提前到達的懲罰因子；d為小麥收割機晚到時所對應的懲罰因子；tig為小麥收割機到達小麥收割點i的時間；wi為小麥收割機提早到達收割點i的時間；vi為小麥收割機最遲到達收割點i的時間。

利用i表示小麥收割機的編號，利用N表示小麥收割點的數目，i=1 表示中心小麥收割機點；g表示布置作業的小麥收割機的編號，G表示小麥收割機的總量。處于作業狀態的小麥收割機的數量定義為Jw，處于閑置狀態的小麥收割機數量定義為Jr，Jw+Jr=G。小麥收割點i和j之間的單位距離成本定義為aij，小麥收割點i和j之間的距離定位為lij，小麥收割機的啟用成本定義為cw，小麥收割機的閑置成本定義為cr，小麥收割機的閑置時間定義為tr，根據以往數據確定的收割點i在單位時間內收割小麥的數量定義為pi，Tig表示小麥收割機g在收割點i的工作時間，ti表示小麥收割機g準時到達收割點i的時間，Ug表示小麥收割機g的作業任務指標。

構建一個決策變量，定義如下：

目標函數包括小麥收割機的路程成本、收割機啟動成本、時間懲罰成本以及小麥收割機的閑置成本，具體方程如下：

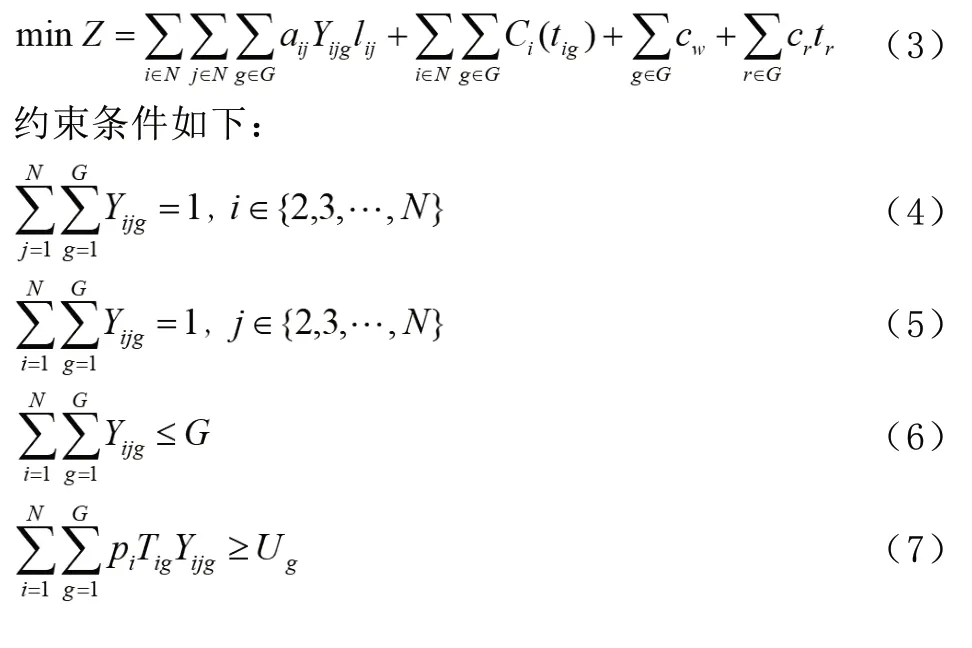
2 改進粒子群算法的基本理論

粒子群算法是依據鳥群的飛行特點確定的，和其他智能算法相比，該算法易于實現，所需調節的參數比較少，在很多工程領域有廣泛的應用。在粒子群算法中，需要求解的問題與粒子群的一個粒子一一對應，粒子的性能可以利用適應度評價，第i個粒子的位置定義為第i個粒子的速度定義為個體的最優位置定義為，全局最優位置定義為經過t次迭代，第i個粒子的速度和位置更新公式如下：

式中：ω為慣性系數；c1與c2為加速因子，兩個因子均大于等于0；r1與r2均為隨機數

常規的粒子群算法存在收斂效率較低和易陷入局部最優的不足，因此，應選取有效的方法對傳統的粒子群算法進行改進。改進粒子群算法的優化過程通常由適應度的大小來確定，通過求出不同粒子目前位置的適應度，對適應度進行排序，適應度排序在后50%的粒子所對應的速度和位置與排序在前50%的粒子所對應的速度和位置進行替換，同時歷史的最優位置處于不變狀態。將遺傳算法引入粒子群算法的改進中，利用選擇操作粒子群可以獲取最優的空間，也受粒子群中個體的最優位置干擾。利用交叉操作，把上一步操作過程中位置發生改變的50%粒子置于同一個池內，在池中粒子進行兩兩交叉，依據一定的交叉概率形成后代粒子替換父代粒子，從而使粒子群中的粒子具有不變的數量。當池中的粒子全都經過了交叉操作，結束交叉操作，后代粒子位置的計算公式如下：

此外，粒子群算法的慣性因子對于優化收斂效率和提高優化精度具有決定性作用，慣性因子增加時，粒子群算法的全局收斂能力將增強，同時具有更高的收斂效率，當慣性因子減小時，粒子群算法的局部尋優能力將增強，同時也延長了算法的收斂時，為優化慣性因子，可以調節慣性系數，讓粒子群算法前期所對應的慣性因子較大，而粒子群算法的后期所對應的慣性因子較小，從而能提高粒子群算法的收斂性能，并且獲得全局尋優性能。慣性系數調整公式如下：

式中：ωmax為最大慣性系數；ωmin為最小慣性系數；t為即時迭代次數；Tmax為最大迭代次數。

3 仿真分析

為了驗證模型的有效性，文章以10 個小麥收割聯合收割機為研究對象進行仿真分析，一共有20 塊小麥田。利用MATLAB 軟件編制仿真程序，粒子群數量為75，最大迭代次數為350，對改進前后粒子群算法分別運行5 次，最終獲得小麥收割機調度成本計算結果，如表1 所示。

表1 小麥收割機調度成本計算結果 單位：萬元

根據計算結果可知，改進后粒子群算法的小麥收割機最優成本明顯小于改進前粒子群算法的小麥收割機調度成本，利用改進后的粒子群算法獲得的最優收割路徑為109.35km，能達到小麥收割機調度效果。

4 結論

文章在分析小麥收割機調度問題的基礎上構建了小麥收割機調度優化模型，并且改進了粒子算法。通過仿真分析可以得出，經過改進后粒子群算法優化的小麥收割機調度成本大大降低，相應的收割路徑也大大縮短，從而提高了小麥收割機調度優化水平。