基于熱點應力法的正交異性鋼橋面板疲勞分析及驗算

周列茅 馬海峰 宣壽通 程 進

（1.溫州市交通發展集團有限公司，溫州 325000；2.溫州甌江口大橋有限公司，溫州 325000；3.同濟大學土木工程學院，上海 200092）

0 引 言

正交異性鋼橋面板的重量輕、承載力高、適用性強，正越來越多地被應用在現代化橋梁結構中［1］。現在國內已建或在建的大跨度橋梁多采用正交異性鋼橋面板，比如蘇通大橋，南京長江二橋，甌江北口大橋，武漢楊泗港長江大橋以及港珠澳大橋等。盡管正交異性鋼橋面板有諸多優點，但其同時也存在著一些不容忽視的問題，其中最突出的就是疲勞問題［2］-5。正交異性鋼橋面板構造較為復雜，存在許多連接焊縫，各主要部位之間均通過焊縫相連，在這些連接部位處存在由焊接加工產生的殘余應力，而且鋼材本身存在著各種各樣的初始缺陷，在各種外部荷載日復一日的作用下，這些焊接部位非常容易產生疲勞開裂的現象［5］。

針對鋼結構的疲勞問題目前已經發展出了許多種分析方法，比如名義應力法和熱點應力法等。名義應力是由簡單的材料力學公式就能推導出的截面平均應力［7］，正因為名義應力法的原理比較簡單，該方法適用于受力狀態較為明確的構件，而對分析受力復雜的結構效果不理想，如正交異性鋼橋面板，多數情況下難以明確焊接部位類型、名義應力大小和位置，且因面外變形引起的結構次內力導致的疲勞損傷無法考慮；此外，名義應力考慮了結構宏觀尺寸的效應，而沒有考慮焊縫的存在，難以代表焊縫局部區域的應力狀態。與名義應力相比，熱點應力更加接近焊趾處的實際應力；對于受力和構造均較為復雜的正交異性鋼橋面板而言，熱點應力法是對其進行疲勞評估更為適用的方法。

本文首先對熱點應力法的基本原理進行了介紹，然后給出了基于熱點應力法的正交異性鋼橋面板疲勞分析及驗算方法，最后采用該方法對某三塔四跨雙層鋼桁梁懸索橋采用的正交異性鋼橋面板進行了疲勞分析及驗算。

1 熱點應力法的基本原理

1.1 熱點及熱點應力

熱點指的是結構中由于應力波動和焊縫幾何形狀或類似切口的綜合效應導致疲勞裂紋萌生的點，一般指焊縫的焊趾處。焊接結構焊趾處的實際應力由3個部分組成，分別為膜應力σmem、殼彎曲應力σben和非線性應力峰σnlp，其中膜應力σmem是平均應力，應力大小沿截面厚度方向保持不變，殼彎曲應力σben的分布與厚度存在線性關系，而非線性應力峰σnlp是一種自平衡力，應力大小與焊縫特性有關。熱點應力包含了除焊縫特性之外的所有構造細節引起的缺口應力，即膜應力σmem和殼彎曲應力σben。

國際焊接協會IIW［8］根據熱點所處的位置以及所在的焊縫焊趾方向將熱點分為了兩種類型，如圖2所示。從圖中可以看出，a類型與b類型熱點的區別在于所處的位置不同，a類型熱點處在焊接構件的外表面上，而b類型熱點處于焊接構件的厚度平面上，這是判斷焊趾屬于何種熱點類型的關鍵。

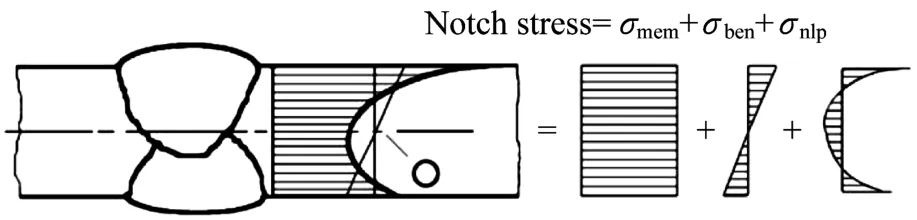
圖1 焊趾處的實際應力Fig.1 Actual stress at weld toe

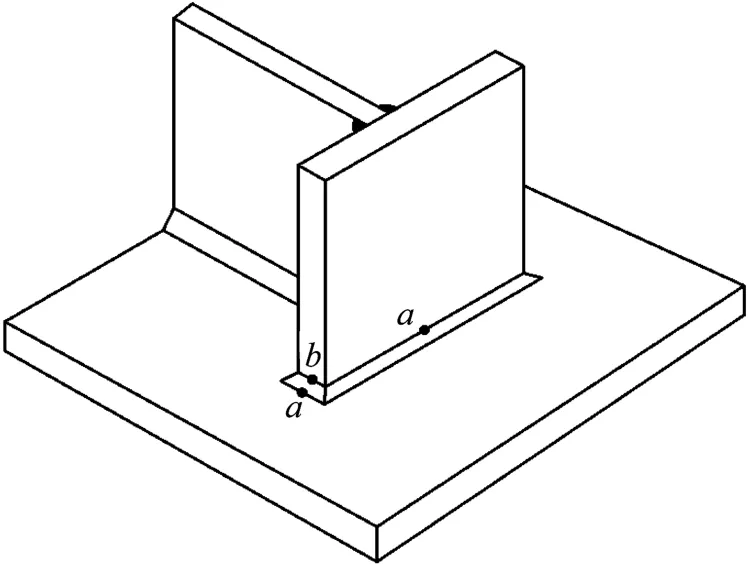
圖2 熱點類型Fig.2 Hot-spot type

1.2 熱點應力的確定方法

熱點應力可以通過有限元分析計算得到，因為有限元模型存在局部不連續性，所以熱點應力不能直接從單元或者節點處提取，只能通過采用一定的插值方法來確定。目前存在的插值方式有很多種，比如厚度線性化法、表面外推法、1 mm法和dang法等，其中應用最多的是表面外推法，國際焊接協會IIW和歐洲船級社［9］都分別給出了各自推薦的表面外推方法，具體公式見表1，不同類型熱點采用的外推公式不一樣。

表1 熱點應力法常用表面外推公式Table 1 Hot spot stress method commonly used surface extrapolation formula

1.3 熱點應力疲勞強度等級

為了確定基于熱點應力法的構造細節疲勞強度等級，相關學者采用表面外推方法對大量疲勞試驗結果進行了熱點應力分析［10］，結果如圖3所示。可以看出，采用名義應力法時分散的試驗結果轉化為熱點應力后變得很集中，且所有計算得到的數據點全部落在AASHTO規范C（FAT90）級S-N曲線的上方，說明名義應力法需要劃分為多種等級的焊接構造，采用熱點應力法時只需要統一的等級就可以涵蓋。因此，采用C（FAT 90）級作為熱點應力疲勞強度等級，即200萬次循環對應的疲勞強度應力幅是90 MPa，常幅疲勞極限即107次循環對應的疲勞強度為52.7 MPa，變幅疲勞截止限即108次循環對應的疲勞強度是33.2MPa。

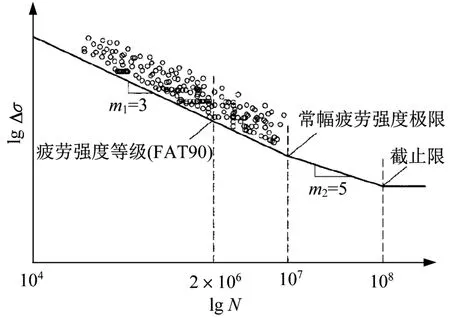
圖3 熱點應力S-N曲線［11］Fig.3 Hot-spot stress S-N curve

2 基于熱點應力法的鋼橋面板疲勞分析及驗算方法

首先針對所驗算的正交異性鋼橋面板建立有限元模型，通過有限元分析確定驗算部位；然后根據熱點應力外推公式采用我國《公路鋼結構橋梁設計規范》中給出的疲勞荷載計算模型Ⅲ［12］，如圖4所示，沿車道縱向行駛加載一次，得到驗算部位的應力歷程；最后采用泄水法計算出應力幅Δσi及對應的循環次數ni，其中最大應力幅為Δσmax，并根據熱點應力S-N曲線確定常幅疲勞極限ΔσD。

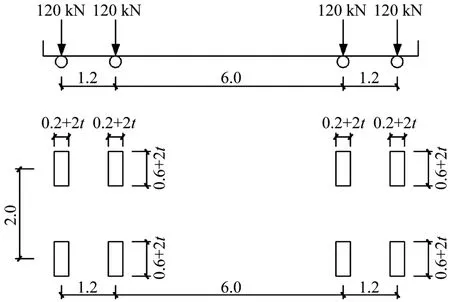
圖4 疲勞荷載模型示意圖（單位：m，t為鋪裝層厚度）Fig.4 Schematic diagram of fatigue load model（Unit：m，t is the thickness of paving layer）

（1）當 Δσmax≤ΔσD，則驗算部位不會疲勞開裂，驗算結束。

（2）當以上①的驗算不滿足，則采用Palmgren-Miner線性累積損傷準則按下式進行變幅疲勞損傷度驗算［14］：

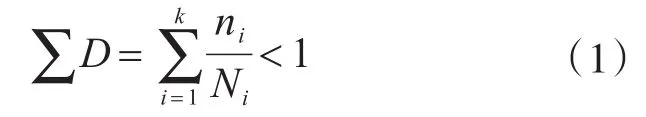
式中，∑D為損傷度，疲勞驗算時應力幅頻值譜中各級應力幅Δσi及其循環次數ni所引起的損傷度Di按以下公式計算：

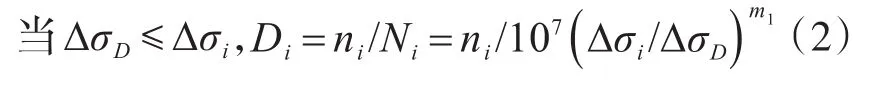
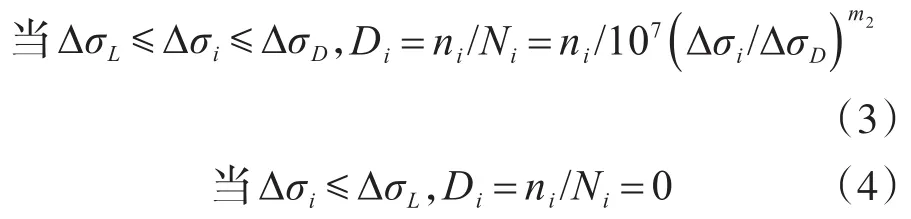
式中，m1、m2為圖3疲勞強度對數曲線的斜率；Ni為Δσi作常幅應力幅循環試驗時的疲勞破壞次數。

根據式（1）計算鋼橋面板疲勞損傷度后，即可根據下式預測鋼橋面板的疲勞壽命L：

3 工程實例

3.1 工程背景

某橋為主跨跨度（800+800）m的三塔四跨雙層鋼桁梁懸索橋，矢跨比采用1/10。加勁梁為板桁組合鋼桁架，橫斷面如圖5所示，橋面分上、下雙層布置，上、下兩層的車行道橋面系均采用正交異性鋼橋面板且構造類似，橫橋向關于加勁梁中心線對稱。

圖5 某橋加勁梁橫斷面圖（單位：mm）Fig.5 Cross-sectional view of a bridge stiffening beam（Unit：mm）

3.2 有限元建模

由于正交異性鋼橋面板構造細節處的疲勞應力主要受到橋面板第二、三體系的影響，故本文采用有限元軟件ANSYS進行數值分析時只建立了鋼橋面板的節段模型。由于該橋上下層車行道交通量的比值約為2∶1，因此上層橋面板受力更加不利，故僅針對上層橋面板進行分析。

正交異性鋼橋面板在車輛荷載下的應力具有很強的局部性，一般模型的縱向長度取2～3個橫隔板間距即可，而且不同疲勞細節處的影響線，縱向影響線長度一般不超過10 m，根據影響線長度并考慮圣維南原理，最終縱向取兩個加勁梁標準節段長度，共20 m；由于橋面結構關于中心線橫向對稱，因此對結構進行對稱性簡化，橫向僅建立1/2橋面，長17.6 m。模型共包括25個U肋、3個節點橫梁和4個節間橫梁。有限元模型中所有構件均采用空間板殼單元SHELL63進行模擬，模型中不建立焊縫，熱點選在兩殼中性面的交點處以避免計算值偏低。本文選取了4種鋼橋面板典型疲勞細節進行研究，分別是：①頂板與U肋焊縫處頂板細節；②頂板與U肋焊縫處U肋細節；③U肋與橫梁焊縫處橫梁細節；④橫梁腹板開孔細節。其中，疲勞細節①和②屬于a類型熱點，疲勞細節③為b類型熱點，疲勞細節④為非焊接細節。對于a類型熱點應力采用兩點線性外推方法計算，b類型熱點應力采用固定點法計算，各疲勞細節附近的單元網格尺寸劃分都嚴格依照外推要求來確定。鋼橋面板的有限元模型如圖6所示。

圖6 有限元模型Fig.6 Finite element model

在有限元模型中，橫橋向為X軸，豎向為Y軸，縱橋向為Z軸。模型的邊界條件為：約束橋面板左側三個方向的平動自由度和繞橫橋向X軸的轉動自由度；橋面板右側采用對稱約束；約束節點橫梁底部所有自由度；約束節間橫梁底部三個方向的平動自由度。根據圣維南原理，由于本文驗算的疲勞細節均距離邊界較遠，故可以認為以上邊界條件對應力的計算影響很小。

鋼橋面板疲勞有限元分析時采用的荷載為我國規范中給出的疲勞荷載計算模型Ⅲ，如圖4所示。車輛總重為480 kN，每個單軸重120 kN，車輛軸距為1.2 m+6 m+1.2 m，橫向輪距為2 m，車輪著地面積為0.2 m×0.6 m。由于荷載模型前后軸之間的距離較遠，且在車輪荷載作用下正交異性鋼橋面板應力分布具有較強的局部性，因此可以不考慮前后軸作用效應的疊加［15］，故下文的分析中只采用疲勞荷載模型Ⅲ中的后軸即120 kN+120 kN的雙聯軸進行加載。在考慮鋪裝層的作用時，取45°的擴散角。

由于鋼橋面板中疲勞細節數量眾多，首先需要確定每種類型的疲勞細節中受力最不利的一處所在的位置［15］，即每一種疲勞細節的分析對象，這里以外側車道為例，介紹加載方式和縱向關注截面的選取。

外側車道共包含6道U肋，根據U肋開口寬度、間距以及車輪作用面積等特點，橫橋向一共取3種加載方式，如圖7所示，加載方式一與二、三間的橫向距離為150 mm；縱橋向一共取8種加載方式，如圖8所示，相鄰加載方式間的縱向距離為800 mm。綜合考慮橫縱向的所有加載方式，一共有24種工況。

圖7 橫橋向加載方式示意圖（單位：mm）Fig.7 Schematic diagram of cross-bridge loading mode（Unit：mm）

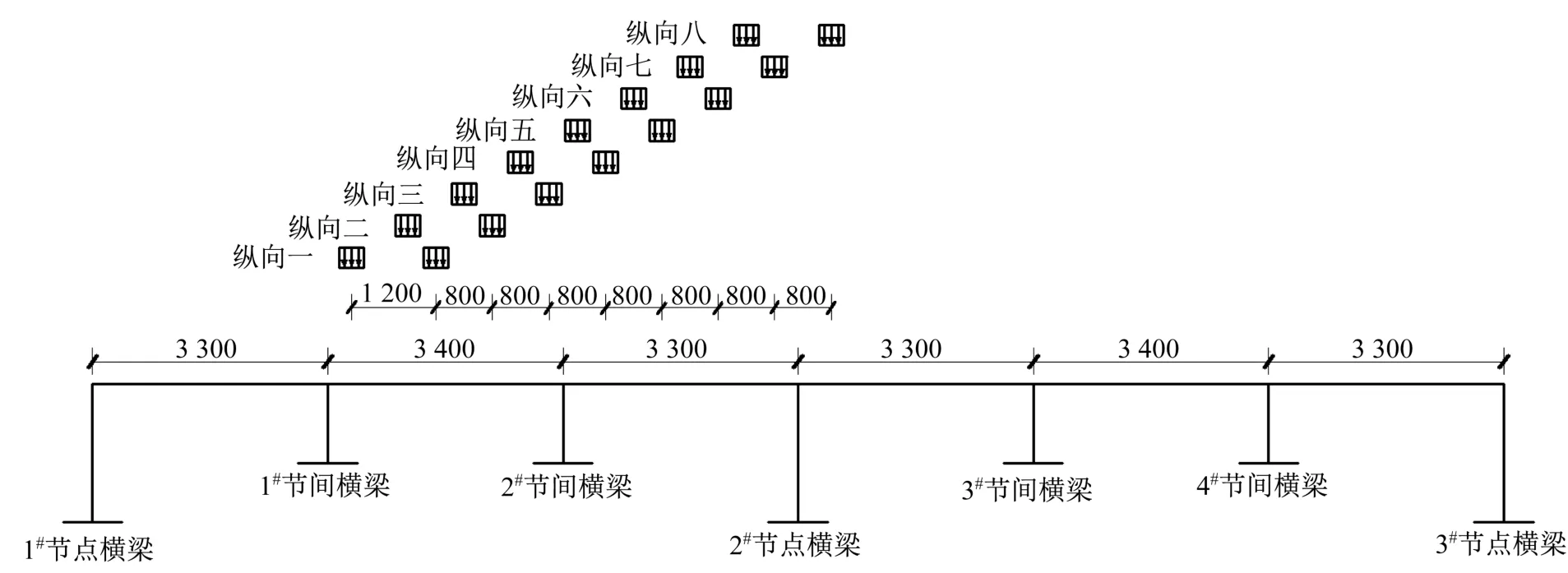
圖8 縱橋向加載方式示意圖（單位：mm）Fig.8 Schematic diagram of longitudinal and bridge loading mode（Unit：mm）

對于疲勞細節①和②，選擇圖9所示的17個縱向截面進行分析，除節點、節間橫梁附近的關注截面距橫梁50 mm外，其余每兩個關注截面間的距離為330 mm；對于疲勞細節③和④，選擇2#節間橫梁和2#節點橫梁進行分析。

圖9 縱向關注截面（單位：mm）Fig.9 Longitudinal section of interest（Unit：mm）

基于上述24種加載工況和若干個縱向關注截面，因為縱橫向考慮的加載工況較多，采用試算方法，基本可以找到各類型疲勞細節中受力最不利的一處所在的位置和所對應的橫向最不利加載方式。

3.4 鋼橋面板疲勞分析

采用上述的車輛荷載以及加載方式進行有限元分析，以“橫向一+縱向二”工況為例，橋面頂板、外側車道下U肋以及2#節間橫梁的應力云圖如圖10所示。從圖10中可以看出，鋼橋面板在輪載作用下的受力呈現明顯的局部性，同時也說明忽略荷載模型前后軸的疊加效應是可行的。

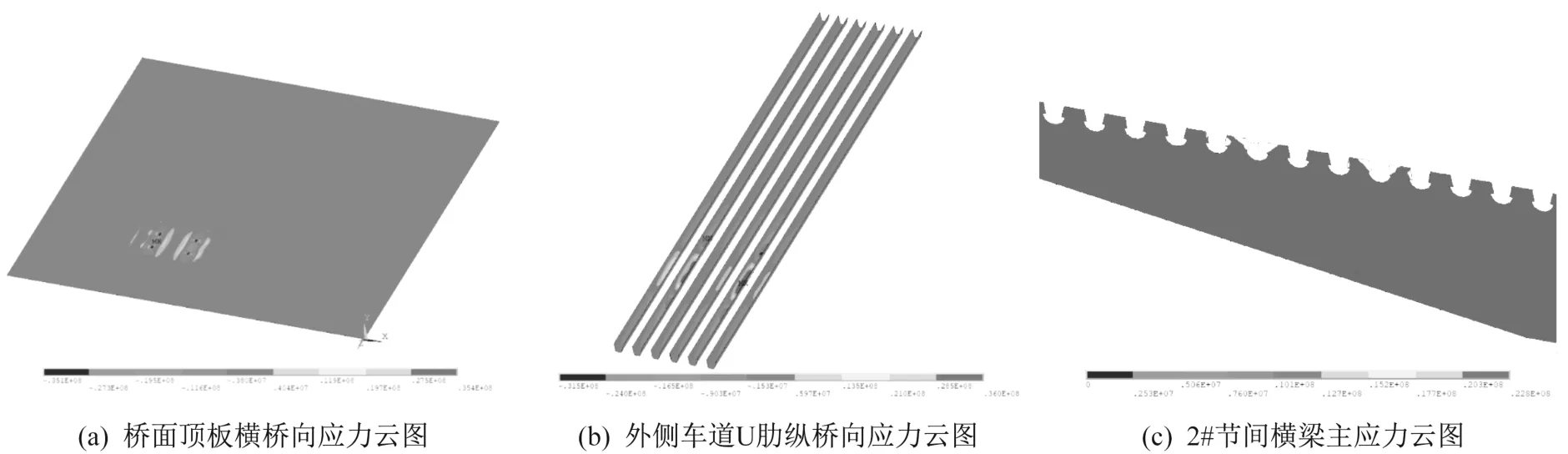
圖10 橫向一+縱向二加載工況下鋼橋面板應力云圖（單位：Pa）Fig.10 Stress cloud diagram of steel bridge deck under transverse one and longitudinal two loading conditions（unit：Pa）

經過在所有加載工況下的分析，最終得到各類型疲勞細節受力最為不利的一處所在的位置以及各自所對應的橫向最不利加載方式，如表2所示。

表2 各種疲勞細節最不利位置及對應橫向最不利加載方式Table 2 The most disadvantaged position and its horizontal loading

3.5 鋼橋面板疲勞驗算

針對各類型疲勞細節的最不利位置開展進一步分析，將疲勞車輛完整行駛加載通過該橋以獲得細節處的實際應力歷程，分析時各疲勞細節的橫向加載位置為上節確定的各自相對應的橫向最不利加載方式。圖11顯示的是在后軸雙聯軸車輪荷載沿有限元模型縱向行駛時，各類型疲勞細節的最不利位置處的應力歷程。

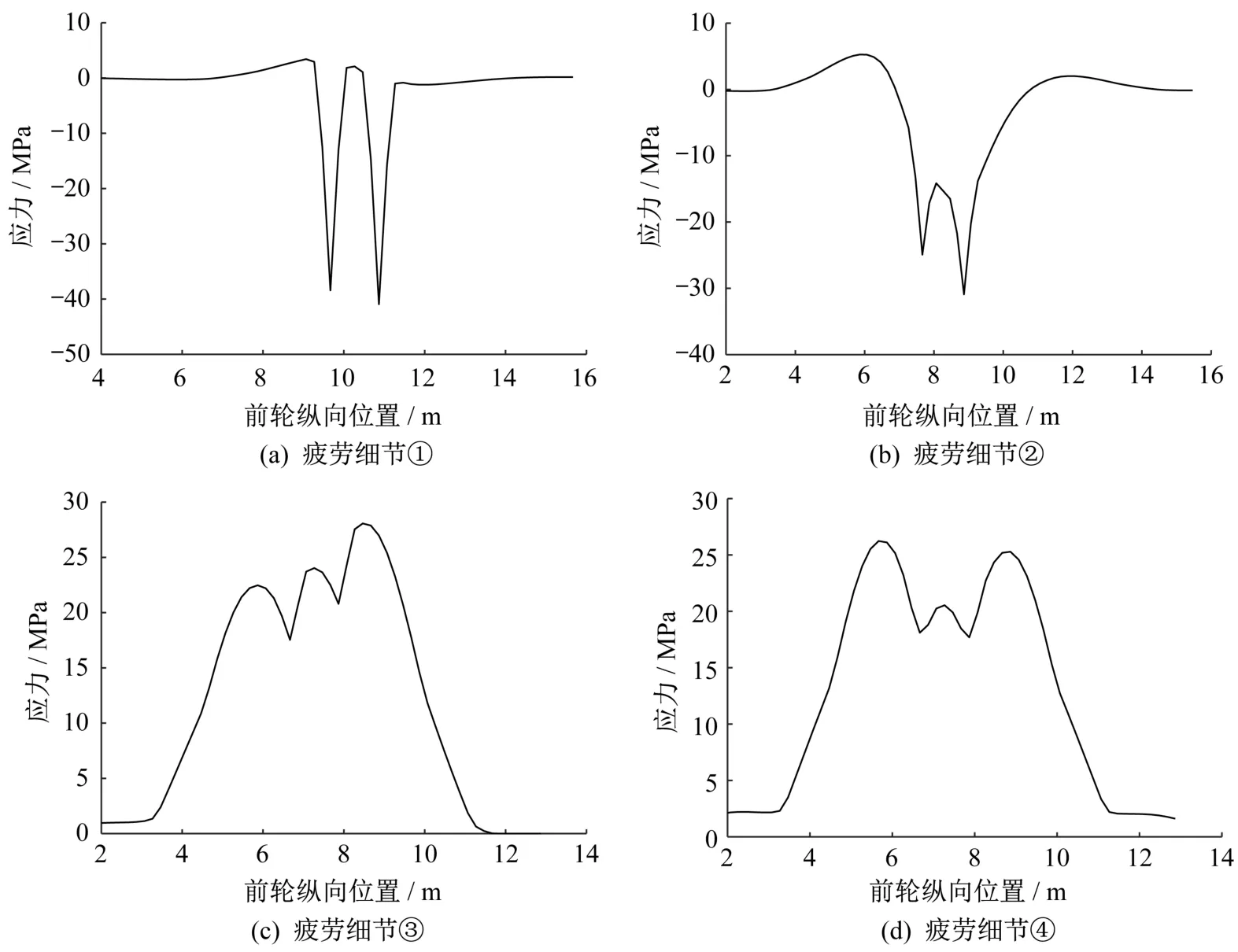
圖11 各疲勞細節應力歷程Fig.11 Stress history of each fatigue detail

在得到圖11所示的應力歷程后，采用泄水法計算各細節的最大疲勞應力幅，對于中間車道根據同樣的方法分析4種疲勞細節處的應力，最終結果見表3。

表3 各疲勞細節最大應力幅Table 3 Maximum stress amplitude of each fatigue detail MPa

如表3所示，在所選取的4種鋼橋面板疲勞細節中，細節①處（即頂板與U肋焊縫處頂板細節）的熱點應力幅最大，為最不利疲勞細節。如前所述，采用FAT90作為熱點應力疲勞強度等級，因此對于細節①、②和③，疲勞強度等級為90，即200萬次疲勞循環對應的疲勞強度應力幅ΔσC為90 MPa，常幅疲勞極限ΔσD為52.7 MPa，變幅疲勞截止限ΔσL為33.2 MPa。細節④為非焊接細節，根據我國規范，疲勞強度等級為70，即200萬次疲勞循環對應的疲勞強度應力幅ΔσC為70 MPa，常幅疲勞極限ΔσD為52.3 MPa，變幅疲勞截止限ΔσL為28.7 MPa。由表3可知，外側和中間車道4種疲勞細節的最大應力幅均低于其對應的常幅疲勞極限，其中，細節③和④的最大應力幅低于其變幅疲勞截止限，說明按照常幅疲勞設計準則進行驗算時這4種疲勞細節均無損傷作用而不會產生疲勞開裂。

4 結 論

本文提出了基于熱點應力法的鋼橋面板疲勞分析及驗算方法，并以某三塔四跨雙層鋼桁梁懸索橋為例，針對該橋采用的正交異性鋼橋面板，利用本文提出的方法開展了鋼橋面板疲勞有限元分析及驗算，從而驗證了該方法的可行性。結果表明：在所選取的4種鋼橋面板典型疲勞細節中，頂板與U肋焊縫處頂板細節的熱點應力幅最大，為最不利疲勞細節；4種疲勞細節的最大應力幅均低于其對應的常幅疲勞極限，說明這4種疲勞細節均無損傷作用而不會產生疲勞開裂。