均勻扭轉體建筑結構的整體性能分析

夏開峰 李啟才

（蘇州科技大學土木工程學院，蘇州 215000）

0 引 言

為了建筑形式的創新，建筑設計師開始在自已的建筑創作中應用扭轉形式。世界高層建筑與都市人居學會（Council on Tall Buildings and Urban Habitat，CTBUH）［1］將這種樓面或者立面隨著高度旋轉而變化的建筑定義為扭轉體建筑。隨著國內外越來越多的扭轉體建筑產生，如達芬奇塔、上海中心大廈和臺北陶朱隱園等，這種結構的整體性能引起了人們的關注。2007年樓國山［2］較為全面地講解扭轉體建筑的建筑設計要求和步驟，但結構分析方面并未具體研究。2008年智平［3］對高層扭轉體型結構體系的力學性能進行了研究，但側重分析結構在風荷載作用下的性能。2015年 Desimone和 Ramirez［4］探討了設計扭轉體建筑物面臨的困難，提出構造措施，但結構分析方面并不全面。2015年馬暉等［5］對深圳前海世茂金融中心塔樓進行了結構分析與設計，側重研究豎向荷載作用下結構傳力機制，并對樓板進行重點設計。扭轉體建筑的實際應用已經超前理論研究。目前國內外對這種扭轉體建筑的整體受力性能方面的分析甚少，缺乏系統化的理論研究。本文將從底層至頂層在高度方向上以均勻角度扭轉的建筑整體結構為研究對象，對其性能進行研究和分析。

1 結構計算模型

選取蘇州地區某賓館的6層鋼框架結構，總高度19 m，底層4 m，其余樓層3 m。為了使建筑呈現線性均勻扭轉的形式，從一層地面開始豎向逆時針扭轉，扭轉率0.666 7°/m（π/270 rad/m），第二層樓面繞樓面中心相對第一層地面扭轉2.667°，其余每層樓面相對下一層樓面旋轉2°，整體結構扭轉12.667°。結構平面為規則的矩形，長36 m，寬18 m。框架平面縱向布置9根柱，柱距為4.5m，橫向布置4根柱，柱距為6m。部分樓面的平面布置如圖1所示。

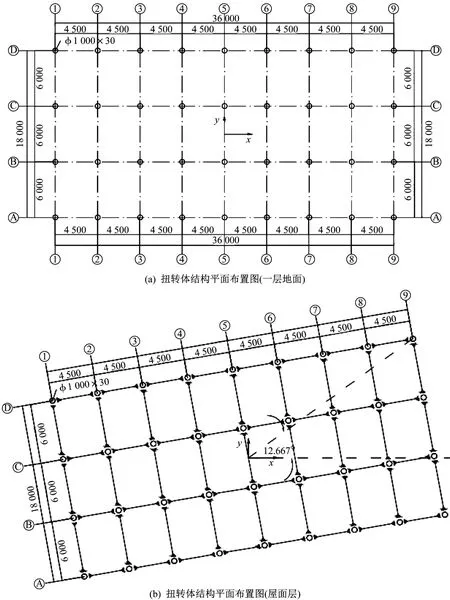
圖1 平面布置圖Fig.1 Plan layout

結構荷載標準值：樓面恒荷載4.5 kN/m2，活荷載2.0 kN/m2，基本風壓為0.4 kN/m2，阻尼比為0.015。結構設計參數見表1。

表1 設計參數Table 1 Seismic design parameters

結構梁柱材料統一采用Q355鋼材，第一層和第二層樓面橫向框架梁采用HN700×300×13×24，縱向框架梁采用HN650×300×12×20；其余層樓面橫向框架梁采用HN400×150×8×13，縱向框架梁采用 HN350×175×7×11。柱統一采用圓鋼管柱φ1 000×30。樓板采用厚度為120 mm的C30混凝土樓板，樓板假定為彈性。

本文運用ETABS軟件對上述扭轉的框架結構建立計算模型，與對應未扭轉的框架結構進行對比，來分析扭轉對結構力學性能影響。扭轉體結構和非扭轉體結構計算模型如圖2所示。

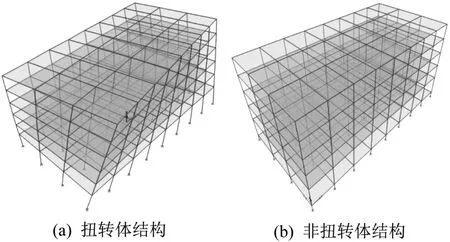
圖2 計算模型示意圖Fig.2 Schematic diagram of calculation model

2 主要分析結果

2.1 分析方法

（1）考慮雙向水平地震作用平扭耦聯的扭轉效應。

（2）分析方法為振型分解反應譜法，分析中考慮重力二階效應的影響。

（3）采用ETABS中的彈性殼單元來模擬樓板，較為真實地反映樓板剛度和變形。

（4）關于扭轉體結構的風荷載體型系數相關規范并未明確給出，這里則參考智平［3］對扭轉體建筑的風洞試驗取值，非扭轉體結構則按照表1取值。

2.2 結構自振周期和振型

對于多層鋼結構周期比的限值，相關規范并未明確規定。由表2可看出扭轉體結構以平動為主的周期大于非扭轉體結構，以扭轉為主的周期小于非扭轉體結構。通過周期比與抗扭性能之間的關系，說明扭轉體結構較非扭轉體結構相對抗扭性能較好。

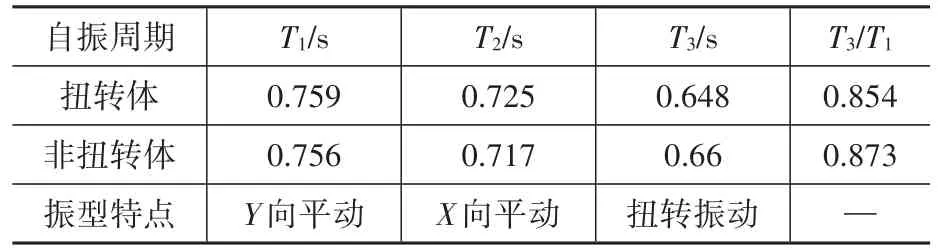
表2 結構自振周期Table 2 Structural natural vibration period

2.3 結構扭轉規則性

分別提取考慮偶然偏心的水平地震作用下扭轉體結構和非扭轉體結構樓層頂板的最大層間位移和平均層間位移，見表3。

表3 結構在偶然偏心水平地震作用下最大層間位移和平均層間位移Table 3 Maximum interstory displacement and average interstory displacement of structures under accidental eccentric horizontal earthquake

由表3看出扭轉體結構第6層頂板Y方向最大位移比為1.199，非扭轉體結構第一層頂板X方向最大位移比為1.005，兩者均小于規定的1.2，按照《建筑抗震設計規范》（GB 50011—2010）［6］規定，兩者均屬于扭轉規則結構。

2.4 結構位移

圖3和圖4分別為扭轉體結構和非扭轉體結構在（1.2×恒荷載+0.6×活荷載+0.28×風荷載+1.3×地震）組合作用下結構整體位移和層間位移角分布比較，圖5為扭轉體結構和非扭轉體結構在（1.2×恒荷載+0.6×活荷載）組合作用下結構的層間位移角比較，圖6為扭轉體結構和非扭轉體結構在（0.28×風荷載+1.3×地震）組合作用下結構的層間位移角比較。通過分析，得出以下具體結論：

圖3 結構整體位移Fig.3 Overall displacement of structure

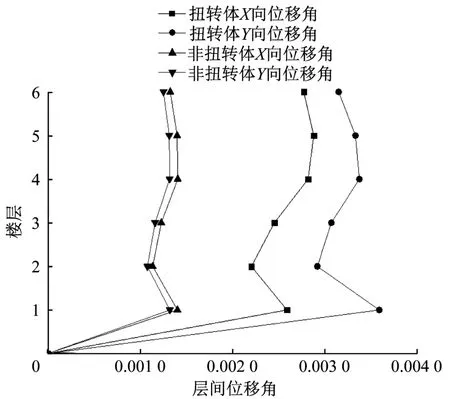
圖4 結構層間位移角Fig.4 Interlayer displacement angle of structure

（1）扭轉體結構X、Y向整體位移最大值分別為49.685 mm和61.84 mm，非扭轉體結構X、Y向整體位移最大值則分別為24.955 mm和23.564 mm。扭轉體結構的兩個方向整體位移遠大于非扭轉體結構，其原因是斜柱在豎向荷載作用下會產生較大的位移所致。

（2）扭轉體結構沿Y軸方向的樓層整體位移大于沿X軸方向，而非扭轉體結構沿Y軸方向的樓層整體位移較接近于沿X軸方向，其中扭轉體結構沿著Y軸主方向的樓層整體位移約為非扭轉體結構的2.6倍。可看出扭轉體結構較非扭轉體結構而言沿弱軸方向的抗側剛度降低更顯著。

（3）由圖4知，扭轉體結構X向最大層間位移角在第五層頂板處最大，Y向最大層間位移角在第一層頂板處最大。非扭轉體結構最大層間位移角都在第一層頂板處最大，因為第一層樓層層高較高，最大層間位移角增幅也較大。而扭轉體結構最大層間位移角遠大于非扭轉體結構最大層間位移角，扭轉體結構Y向最大層間位移角約為非扭轉體結構的3倍，由此可見扭轉對結構變形存在巨大的影響。扭轉體結構因為柱存在傾斜角度，使得柱要分出一部分剛度來抵抗豎向荷載分量產生的扭矩，這便使得柱產生一定的抗扭剛度，也導致扭轉體結構的抗側剛度小于非扭轉體結構。

（4）由圖5和圖6可知，扭轉體結構豎向荷載作用下產生的Y向最大層間位移角為0.002 44，約為對應樓層Y向水平荷載作用下層間位移角0.001 337的2倍。而對于非扭轉體結構豎向荷載產生的變形影響可忽略不計，水平荷載下產生的最大層間位移角為0.001 635。可見扭轉體結構與非扭轉體結構最大的區別在于豎向荷載下的變形特征，扭轉體結構較非扭轉體結構受豎向荷載影響較大。

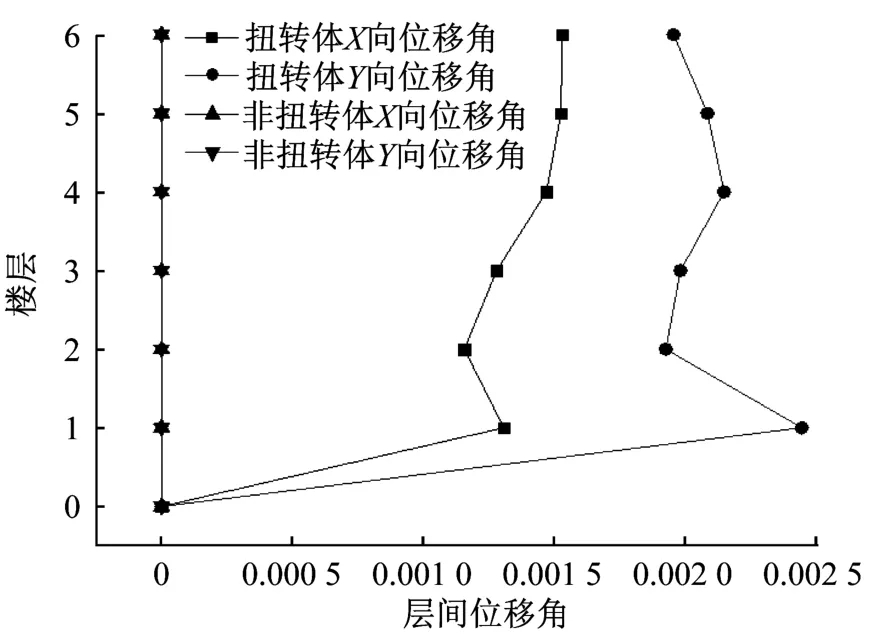
圖5 豎向荷載作用下結構層間位移角Fig.5 Displacement angle between structural layers under vertical load

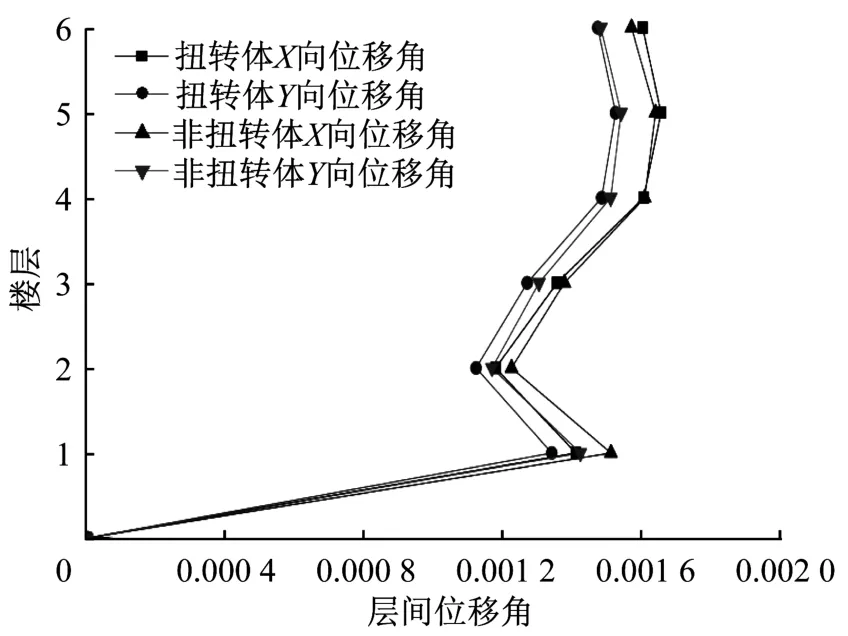
圖6 水平荷載作用下結構層間位移角Fig.6 Displacement angle between structural layers under horizontal load

3 結構內力影響因素

3.1 扭轉對結構的影響

3.1.1 扭轉使柱傾斜產生的影響

本文扭轉體結構模型通過沿高度方向上均勻扭轉樓面再連接柱形成，導致柱出現一定程度的扭轉傾斜。為方便了解柱傾斜對扭轉體結構造成的影響，從圖2的多層扭轉體和非扭轉體整體結構中，提取單層單跨結構進行分析，如圖7所示。扭轉體結構扭轉角度為2°，層高為3 m，柱采用材料為Q355的圓鋼管柱φ550×20，樓板采用100 mm厚的C30混凝土樓板。為了更清楚地分析扭轉對結構的影響，假定樓板為剛性，模型中不加入框架梁，直接將樓板和柱采用剛性連接。非扭轉體結構采用與扭轉體相同的截面和材料，不計自重。扭轉體結構受豎向荷載作用影響較大，在樓板上施加1 kN/m2的豎向荷載進行彈性分析。由于各柱內力計算值基本上完全相同，所以僅提取其中一根柱內力進行分析。

圖7 平面布置圖（單位：mm）Fig.7 Floor plan（Unit：mm）

首先研究柱繞縱軸存在扭轉角的受力條件，如圖8和圖9所示，樓板繞截面中心Z軸，相對于下一層樓板扭轉θ角度，柱截面中心至樓板截面中心距離為ρ。在圖8中，假設任意一根柱DE，因樓面扭轉而位移到了DE′，連接ES和E′S（S為整體結構剪心線上與E、E′共面的一點），則ES和E′S之間夾角為θ。設DE和DE′之間夾角為α，水平面內E和E′到樓板截面剪心S距離均為ρ。由于傾斜，作用在柱上端E′處的豎向荷載P產生分力P′，它繞剪心S形成了扭矩P′ρ，如圖9所示。

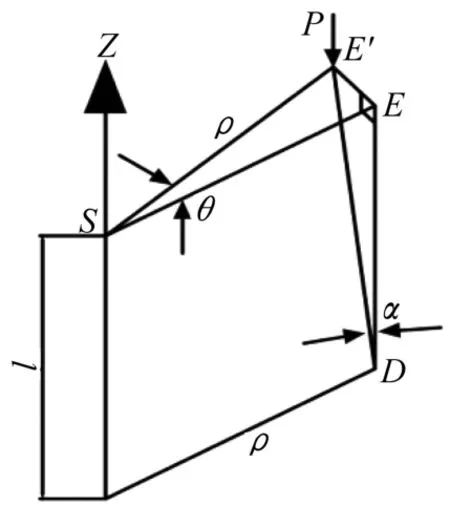
圖8 柱扭轉變形示意圖Fig.8 Schematic diagram of column torsion deformation

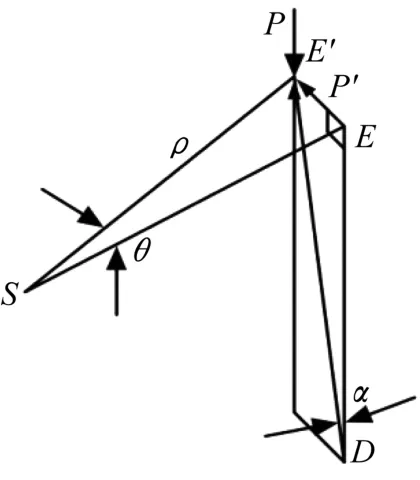
圖9 力分解示意圖Fig.9 Schematic diagram of force decomposition

由于傾斜夾角α很小，故

柱上端水平分力則為

將式（1）代入式（2）后可得到水平分力P′

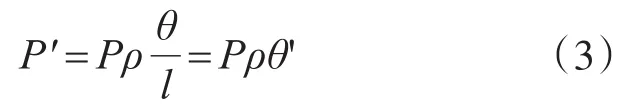
水平分力P′形繞剪心S形成的扭矩

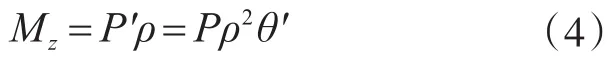
所以理論上柱因傾斜會對結構產生繞樓板中心的整體扭矩Mz。

扭轉體柱存在沿扭轉切向剪力F2-2和沿扭轉法向剪力F3-3，扭轉體柱F2-2與F3-3合力為，方向如圖10所示。

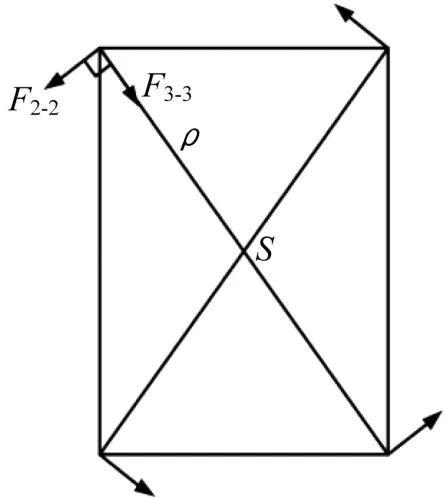
圖10 扭轉體柱剪力合力方向示意圖Fig.10 Schematic diagram of the resultant shear force of twisting

每根柱所受豎向荷載P=1×4.5×6÷4=6.75kN，

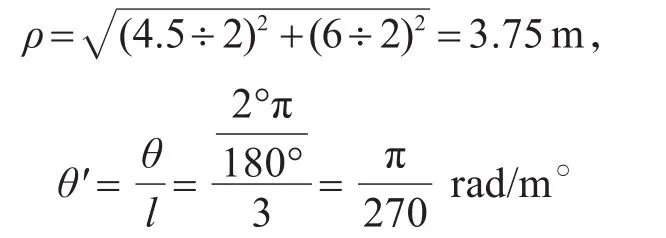
由上述理論公式可得每根柱造成的整體結構扭矩為

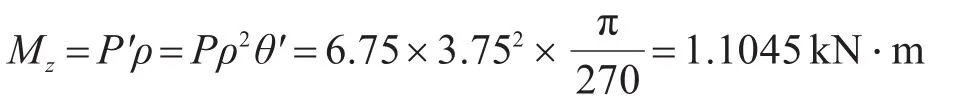
每根柱所受扭矩理論值為：（其中D為圓鋼管柱直徑）

每根柱所受軸力理論值為

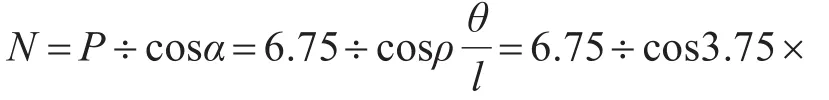
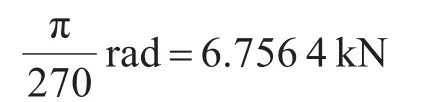
每根柱所受剪力理論值為

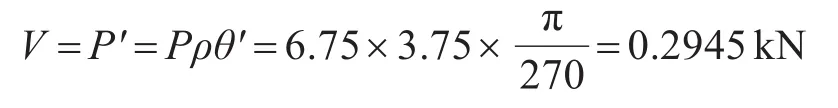
由表4可知，在剛性樓板假定中，扭轉體結構柱相較于非扭轉體結構柱軸力減小0.067%，產生剪力合力約0.251 1 kN，另外還出現扭矩0.161 8 kN·m和彎矩，而非扭轉體柱中只存在軸力。這說明在剛性樓板假定中，扭轉體結構柱因傾斜自身產生一定的扭矩，并對整體結構也產生較大的扭矩。由表5可得理論值與計算值相比剪力誤差較大，誤差可能由扭轉產生的其他因素造成。

表4 扭轉體和非扭轉體框架柱內力Table 4 Internal force of twisted and non-twisted frame column

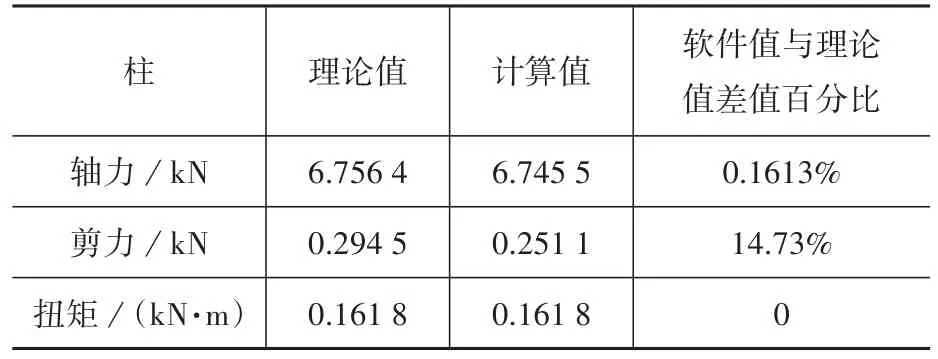
表5 扭轉體結構柱理論值與軟件計算值對比Table 5 Comparison of theoretical value of twisted structure column and software calculation value

3.1.2 扭轉對梁造成的影響分析

為分析扭轉對梁構件產生的影響，現對上述圖7扭轉體和非扭轉體結構加上材料為Q355的框架梁HN400×200×7×11。截面材料、施加荷載不變，假定樓板為彈性，不計自重。其中扭轉體和非扭轉體結構縱向框架梁按局部坐標軸1方向（箭頭向右），橫向框架梁按局部坐標軸1方向（箭頭向上）分別提取梁端和梁跨中內力結果，ETABS中梁的局部坐標軸如圖11所示，2方向垂直平面向上為正方向。

圖11 梁局部坐標示意圖Fig.11 Schematic diagram of beam local coordinates

由表6可知，扭轉體結構梁C′左端軸力較非扭轉體結構C梁減小14.71%，而右端軸力增大13.75%；扭轉體結構E′梁2—2向剪力較非扭轉體結構E梁方向相反，大小基本相等；扭轉體結構C′梁左端3—3向剪力較非扭轉體結構C梁減小82.35%，而右端增大117.23%。這說明扭轉對梁內力方向存在一定的影響，對軸力和3—3向剪力影響較大，扭轉對梁扭矩幾乎不存在影響。

表6 彈性樓板假定下非扭轉體結構和扭轉體結構梁內力Table 6 Internal forces of non-twisted structure and twisted structure beam under assumption of elastic floor

3.2 樓板變形對結構的影響

2015年Desimone和Ramirez等［4］設計扭轉建筑物時，提出樓板要采用彈性樓板假設，同時由圖8可看出豎向荷載分解的水平分量由樓板來承擔，樓板的設計至關重要。為具體分析彈性樓板變形對結構內力產生的影響，分別采用彈性樓板和剛性樓板假定，建立與上述圖7相同材料截面和荷載的單層扭轉體和非扭轉體結構。提取各柱的內力。

通過不同樓板假定下的結構數據對比發現：

（1）非扭轉體結構。在剛性樓板假定和在彈性樓板假定下，柱軸力不變，同時樓板變形作用使1A、1B柱產生同向1.122 8 kNF2-2，1A、1B柱產生相反方向1.705 8 kNF3-3。1A、1B柱產生相反方向扭矩0.019 kN·m，柱底產生最大彎矩1.395 8 kN·m。

表7 扭轉體和非扭轉體框架柱內力Table 7 Internal force of twisted and non-twisted frame column

（2）扭轉體結構。對于剛性樓板假定，樓板只傳遞荷載不發生變形，柱為理想狀態下的受力情況。而在彈性樓板假定下，1B柱較剛性樓板扭轉體結構柱軸力增大0.071%，F2-2減小29.5%，F3-3增加約2 kN，扭矩則反向減少56.2%；1A柱軸力減小0.139%，F2-2增大70.1%，F3-3增加大約2 kN，扭矩則反向減小33.1%。

（3）在彈性樓板假定下，扭轉體結構柱的平均扭矩約為非扭轉體結構柱的5倍，3—3向平均剪力約為1.18倍，這說明樓板變形對扭轉體結構柱的影響更大。在實際結構中，彈性樓板假設更能反映結構的受力和變形，且二者差別較大，所以，扭轉體結構應采用彈性樓板假設進行內力計算。

4 結論

（1）扭轉使柱抗側剛度減小，柱產生一定的扭轉變形，導致扭轉體結構的抗側剛度小于非扭轉體結構。所以，扭轉體結構的整體側移遠大于非扭轉體結構。

（2）扭轉體結構與非扭轉體結構最大的區別在于豎向荷載下的變形特征，扭轉體結構較非扭轉體結構受豎向荷載影響較大。

（3）結構整體扭轉對梁內力方向存在一定的影響，對軸力和3—3方向剪力值影響較大，對梁扭矩幾乎不存在影響。

（4）扭轉體結構較非扭轉體結構而言，柱的剪力和扭矩受彈性樓板作用影響較大。扭轉體結構需采用彈性樓板假設進行計算分析。