數據采集系統非典型采樣故障的特征識別與定量表征

梁志國

(航空工業北京長城計量測試技術研究所 計量與校準技術重點實驗室,北京 100095）

0 引言

任何儀器與系統的使用過程中,均可能產生故障。其中,有一類故障的發作具有偶然性和條件性,在正常使用過程中很難被發現,且故障機理和發生條件不夠明確且復現性差。這里,我們稱其為非典型故障。實際上,在電子儀器設備中,元器件的軟擊穿,焊點的虛焊,接插件的松動等,均可能導致這類非典型故障出現。之所以稱其為非典型故障,主要是因為在大多數使用條件下,它們極少發生并被有效識別。而故障一旦發生,便會造成明顯的錯誤結果。數據采集系統非典型采樣故障便具有這類特征,它很難被遇到、發現和有效識別,故障原因、機理等尚不明確,所帶來的危害更加隱蔽,對其進行識別、表征和深入研究十分迫切。

關于數據采集系統采樣故障的識別與診斷,已有很多卓有成效的工作,一些研究重點針對采樣數據系統的故障開展[1-3],另外也有側重于診斷方法[4]、復雜系統的研究[5],以及特別針對傳感器的故障診斷研究[6-7]。其后,非均勻采樣系統的故障診斷也被涉及[8-10]。無論是提出問題[11],進行濾波[12],還是設計具體的故障觀測器[13],它們分別以不同的理論方法,從時域、頻域、傳遞函數、濾波器等不同的角度進行識別,其多數目標,都是針對比較確切的具有良好復現性的采樣故障情況,共同的特點是過程比較復雜繁瑣,實現起來并不容易。對于復現性較低的非典型采樣故障,考慮得比較少。

對于使用具有非典型故障的儀器設備的人們而言,相當于在伴隨一枚未知爆炸時間的定時炸彈在工作,何時爆炸,以及損失會有多大,則完全取決于其所工作的場所和任務性質。因此,針對非典型采樣故障數據的深入分析和定量表征,對于后續的故障機理分析,故障源頭定位,并最終進行故障排除,具有重要的意義和價值。

本文選取了計量校準工作中發現的一臺具有非典型采樣故障的數據采集系統的故障數據,進行詳細分析,對其故障特征進行了確切表征。

1 故障特征及識別

ZJZ-044A數據采集系統是一種插卡式多通道通用數據采集系統,擁有32個測量通道,A/D位數12 bit,量程范圍±5 V。其在進行誤差限、線性度、直流增益等靜態特性校準中,均未發現異常。而在進行動態有效位數校準中,發現正弦波擬合結果發散,無法獲得正常有效的正弦擬合結果。經過對原始采樣數據的調取,發現其采集曲線波形如圖1所示,存在多個波形規律不連續的故障點。

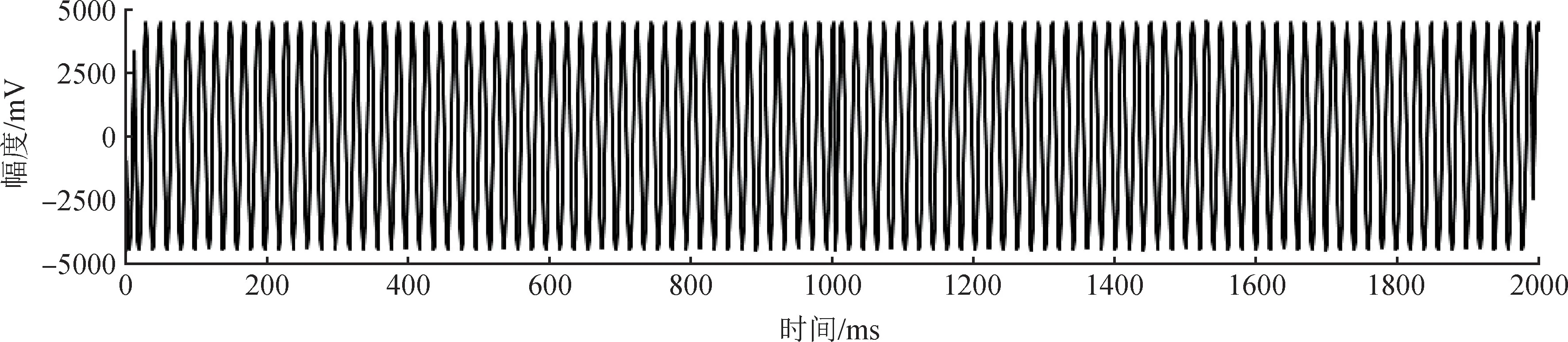
圖1 數據采集系統故障數據Fig.1 Failure data of the data acquisition system

其中,所用的標準信號源為FLUKE5700A多功能校準器,輸出的正弦信號幅度為4.5000 V,頻率為49.000 Hz。數據采集系統的采樣速率為1 kSa/s,數據序列長度為n=2000點。

2 故障特征分析及表征

從圖1所示的曲線可見,在全部2000個采樣點中,t0,t1,…,t1999時刻里,存在故障跳變的時刻點分別為t13,t1004,t1992時刻點。

表現形式為

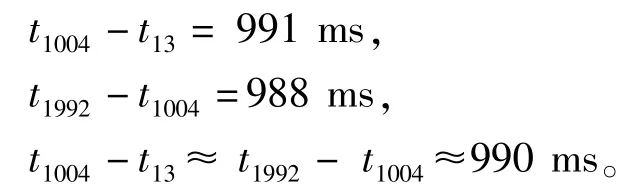
在這三個故障點上,出現了正弦波形規律的不連續,似乎被人為切掉了一部分。其局部細化波形分別如圖2～圖4所示。

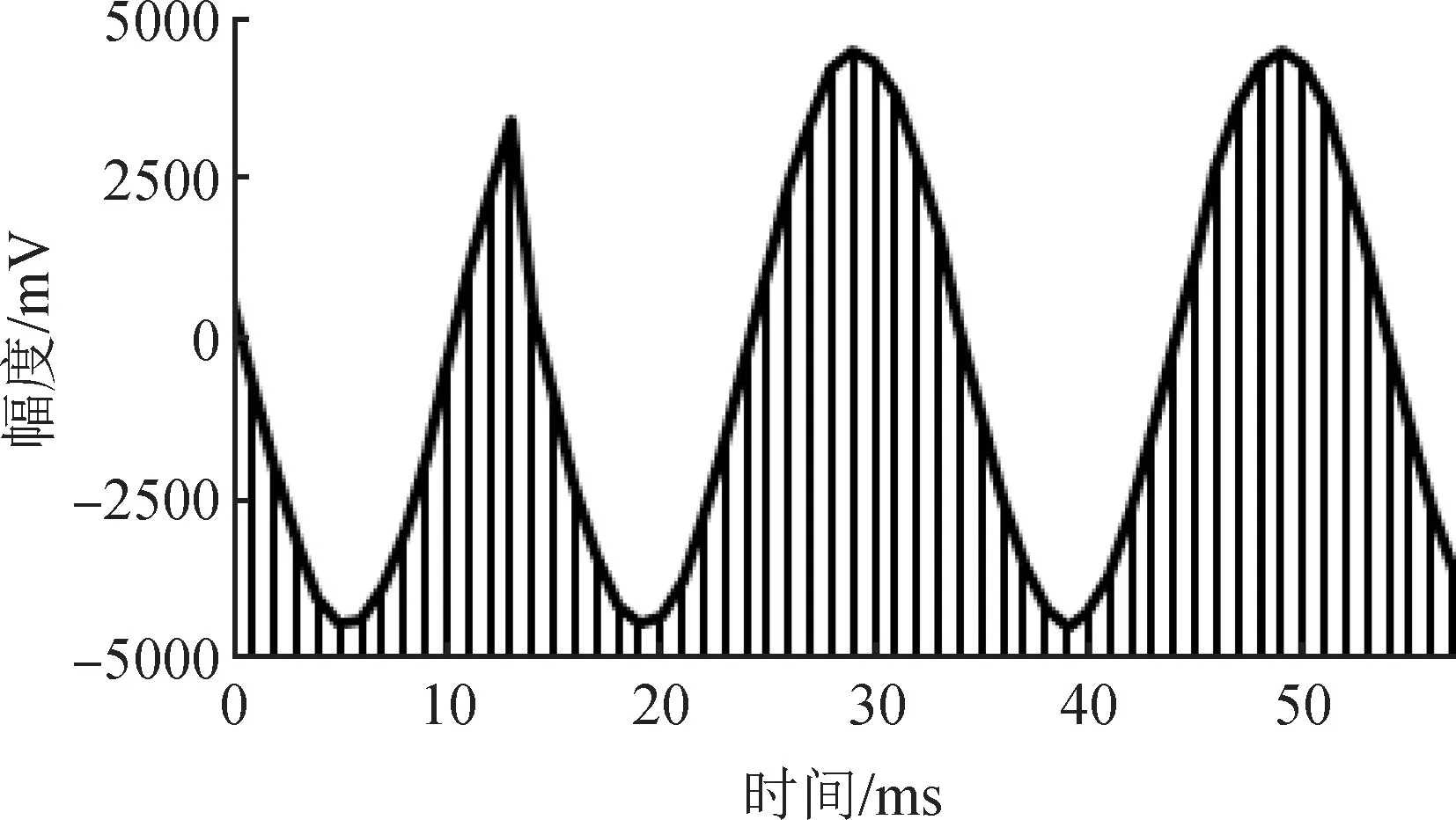
圖2 故障點t13附近的局部波形圖Fig.2 Local waveform near the fault point t13

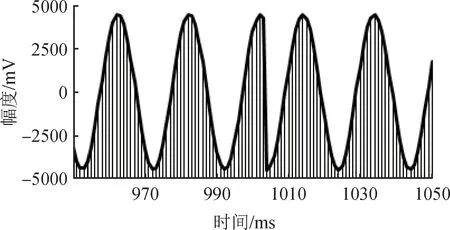
圖3 故障點t1004附近的局部波形圖Fig.3 Local waveform near the fault point t1004

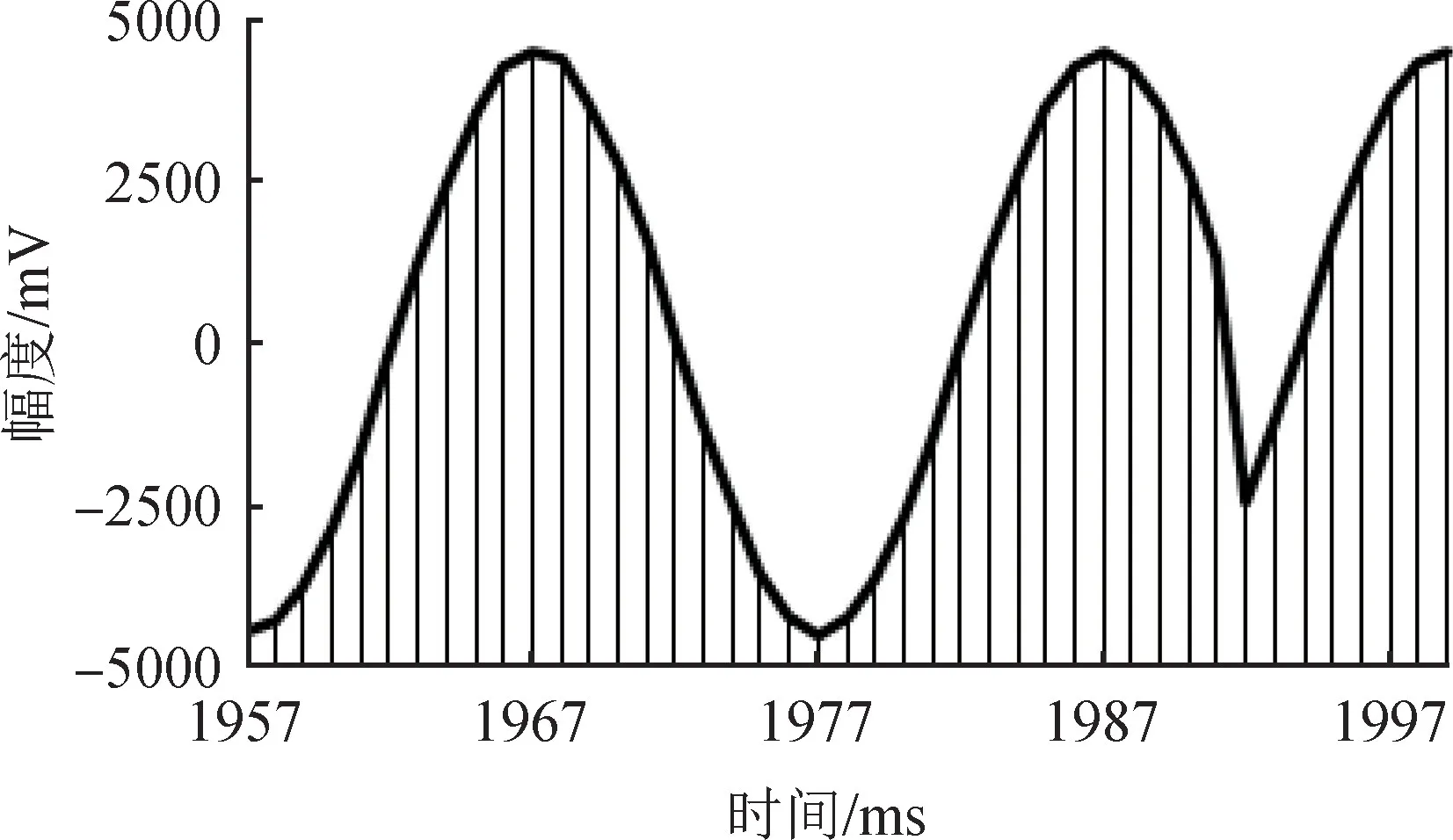
圖4 故障點t1992附近的局部波形圖Fig.4 Local waveform near the fault point t1992

對于故障點處的波形是否真正是“切掉”了一部分波形,以及“切掉”的波形部分有多大,本文將使用模型化處理方式進行識別。

將圖2所示第1個故障點之前的共14點局部正常波形曲線單獨提取出來,進行正弦擬合[14],獲得擬合參數如表1所示。

表1 實測曲線段擬合結果Tab.1 Fitting results of measured curve segments

將擬合波形拓展到全部采樣點上,如圖5中虛線部分所示,稱其為拓展曲線。

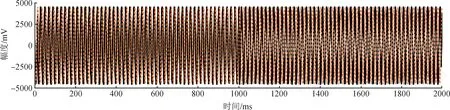
圖5 數據采集系統故障曲線及拓展曲線Fig.5 Failure curve and expansion curve of the data acquisition system

將第1個故障點之后、第2個故障點之前的穩定正常曲線段與對應的拓展曲線段進行900點截取,獲得如圖6所示的波形曲線。

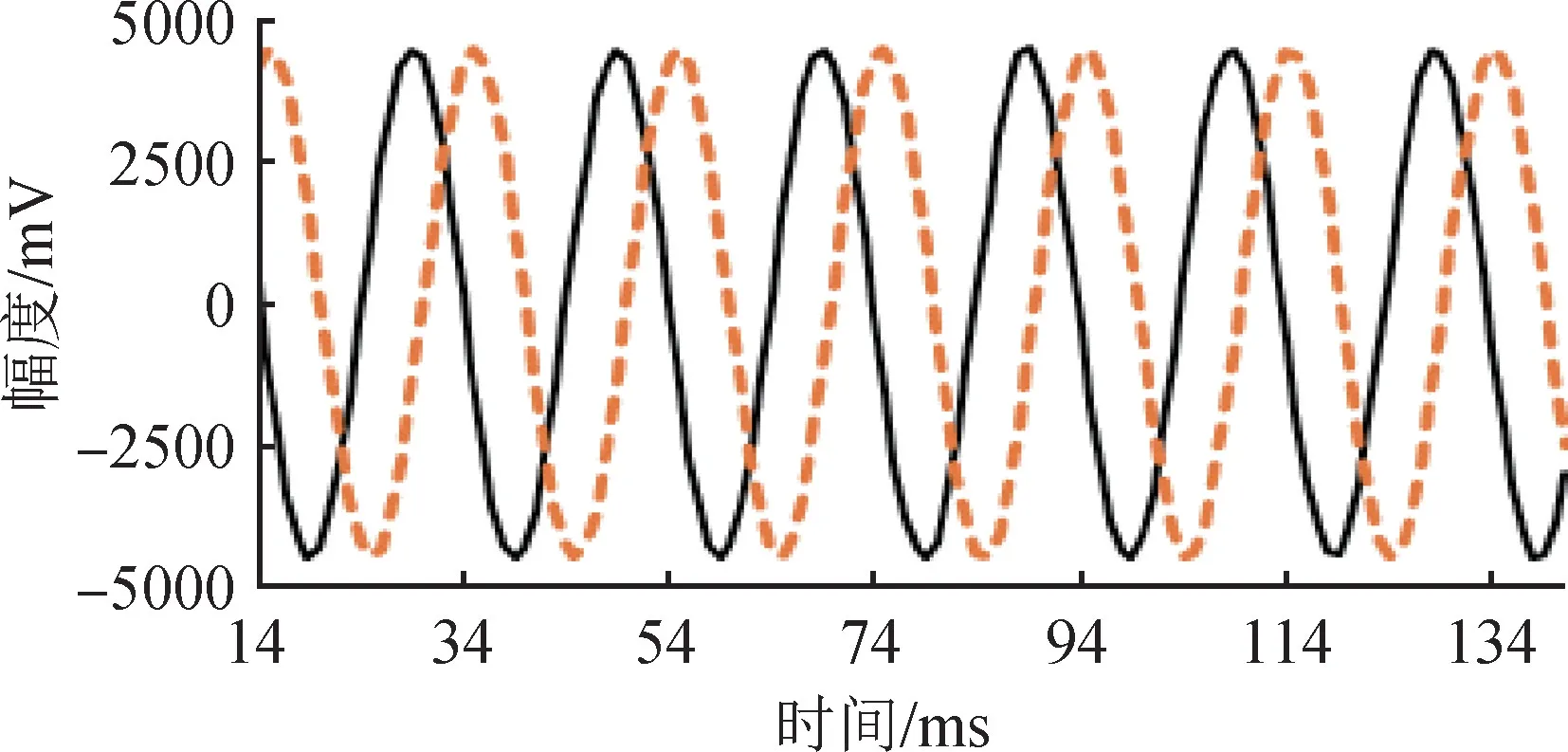
圖6 故障點1之后曲線與拓展曲線(局部)Fig.6 Measured curve and expansion curve after fault point 1(partial)

然后,分別擬合[15],獲得擬合參數如表2所示。

表2 實測曲線段與拓展曲線段擬合結果Tab.2 Fitting results of measured curve segment and extended curve segment

由此,獲得圖6實測曲線段相對于拓展曲線段的延遲時間差為[16-17]

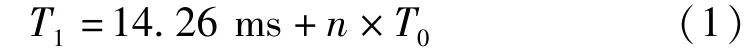
式中:T0為被測正弦信號的周期,T0=1/49 s;n為0或者某一正整數。不失一般性,此處設n=0。

第1個故障點導致采集出現了斷裂點,其后的波形被延遲了時間τ1=T1=14.26 ms。

將第2個故障點之后、第3個故障點之前的穩定正常曲線段與對應的拓展曲線段進行900點截取,獲得如圖7所示的1004 ms以后的波形曲線。

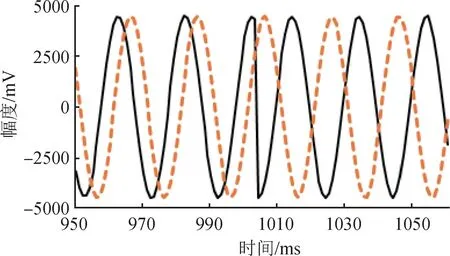
圖7 故障點2左右的實測曲線與拓展曲線Fig.7 Measured curve and extended curve around fault point 2

然后,分別擬合,獲得擬合參數如表3所示。

表3 實測曲線段與拓展曲線段擬合結果Tab.3 Fitting results of measured curve segment and extended curve segment

由此,獲得故障點2之后的實測曲線段相對于拓展曲線段的延遲時間差為

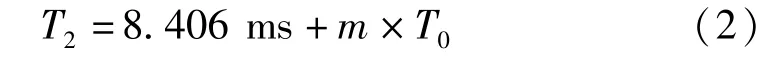
式中:m為0或者某一正整數。

第2個故障點導致采集出現了斷裂點,其后的波形被延遲了時間τ2=T2-τ1。

由τ2＞0,可以判定m=1,τ2=14.55 ms。

將第3個故障點之后的穩定正常曲線段與相應拓展曲線段進行截取,獲得曲線如圖8所示,其中1992 ms點處開始直至結尾部分的8個點屬于異常曲線。

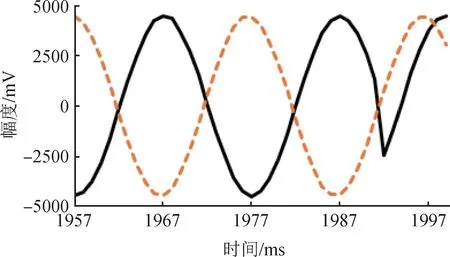
圖8 故障點3左右的實測曲線與拓展曲線Fig.8 Measured curve and extended curve around fault point 3

然后,分別擬合[14],獲得擬合參數如表4所示。

表4 實測曲線段與拓展曲線段擬合結果Tab.4 Fitting results of measured curve segment and extended curve segment

由此,獲得圖8故障點3之后的實測曲線段相對于拓展曲線段的延遲時間差為

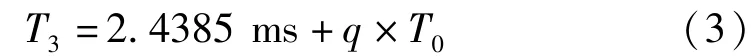
式中:q為0或者某一正整數。

第3個故障點導致采集出現了斷裂點,其后的波形被延遲了時間τ3=T3-τ1-τ2

由τ3＞0,可以判定q=2,τ3=14.44 ms。

3 討論

從上述故障數據曲線及分析過程可見,該故障屬于數據采集系統中極為少見的非典型采樣故障,而非信號受意外干擾產生的粗大誤差。該曲線的波形中,共有3個故障數據點,由于是針對正弦信號進行的數據采集,每次故障出現前后的部分,均屬于正常的正弦信號波形,僅在故障點處出現了波形規律的不連續,該故障在進行直流和變化緩慢的信號波形測量采集中很難被有效發現和識別,在采樣序列長度不夠大時也很難發現,只有在測量已知的標準信號波形并且采樣序列長度足夠大時,才有可能被發現和識別。其每個故障點處造成的波形延遲約為14 ms,近似恒定;兩個故障點之間的時間間隔約為990 ms,近似相等。

從波形數據上看,在每一個故障點后并未出現故障恢復的過渡過程。若存在過渡過程,需要在結束過渡過程的“正常”曲線波形部分進行截取擬合以獲取故障恢復時間才可獲得準確測量結果。過渡過程本身,則可以從實測曲線與擬合回歸曲線之間的差異中獲取。

結合各個故障點的故障信息及其相互間的位置關系,可以初步判定,該非典型采集故障可能屬于數據采集系統中采樣控制計數器相關的故障,它每間隔約990 ms發作一次,約需14 ms才能從故障狀態恢復正常。

若數據采集系統的采集過程使用的是輪詢式采集方式,則輪詢計數器有可能在990左右的計數值附近出現異常,或者計數時鐘在990 ms的間隔存在異常隱患。

若數據采集系統的采集過程使用的是中斷式采集方式,則控制中斷的堆棧計數器有可能在990左右的計數值附近出現異常阻塞或溢出錯誤。

若數據采集系統的采集過程使用的是DMA采集方式,則DMA控制器的地址計數器有可能在990左右的計數值附近出現異常。

該故障也可能是由于A/D轉換狀態指示電平工作不正常造成的,當A/D轉換完畢后,需要變動其完畢狀態指示電平(由低到高,或者由高到低)表示其數據轉換已經完成,可以讀取了。若該電平變動異常,則導致相應讀取數據的操作遲遲不能被執行,也會導致出現這種不連續的斷點故障。

該故障的定位、維修、維護,可以從這些方面著手進行。

4 結論

綜上所述,針對本文所述這類波形規律不連續的非典型采樣故障的數據采集系統,使用正弦激勵,利用分段正弦擬合方式進行故障參數識別是一種切實可行的方法。該方法不僅可以判別出每次采樣故障的恢復時間,以及在故障恢復過程中是否存在過渡過程,還可以判斷出相鄰故障點之間的時間間隔,從而進行更為確切的故障判別與診斷。

非典型采樣故障數據采集系統的故障分析與表征方法和過程總結歸納如下:

1)利用正弦信號對數據采集系統進行激勵,獲得含有p處不連續的非典型采樣故障的采樣序列,并且從起始點開始的一段波形曲線是正常無故障波形;

2)截取起始點開始的一段正常無故障波形進行正弦擬合,獲得擬合曲線,并將其拓展到全序列,形成拓展序列;

3)將第1個故障段之后、第2個故障段之前的穩定正常曲線段與對應的拓展曲線段進行波形截取。然后,分別擬合,獲得實測曲線段擬合參數,以及拓展曲線段擬合參數。

計算獲得實測曲線段相對于拓展曲線段的延遲時間差為

式中:T0為被測正弦信號的周期;Δt1為兩條曲線直接的相位差對應的時間差;n為0或者某一正整數。不失一般性,此處可設n=0。

第1個故障點導致采集出現了斷裂點,其后的波形被延遲了時間τ1,τ1=T1。

4)將第k個故障段之后、第k+1個故障段之前的穩定正常曲線段與對應的拓展曲線段進行波形截取。然后,分別擬合,獲得實測曲線段擬合參數,以及拓展曲線段擬合參數。

計算獲得實測曲線段相對于拓展曲線段的延遲時間差為

式中:Δtk為兩條曲線直接的相位差對應的時間差;m為0或者某一正整數。

第k個故障點導致采集出現了斷裂點,其后的波形被延遲了時間τk。

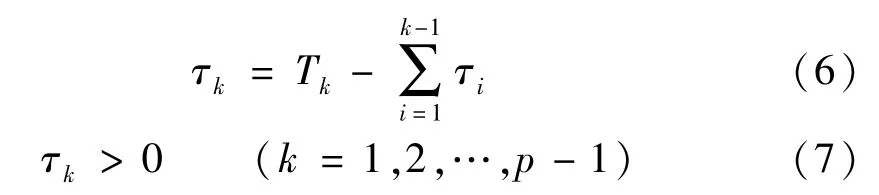
由式(6)、式(7)判定m的取值。

5)將第p個故障段之后直至序列結尾的穩定正常曲線段與對應的拓展曲線段進行波形截取。然后,分別擬合,獲得實測曲線段擬合參數,以及拓展曲線段擬合參數。

計算獲得實測曲線段相對于拓展曲線段的延遲時間差為

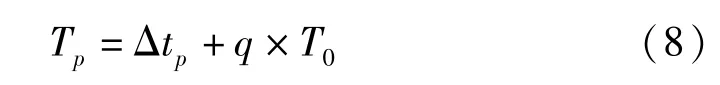
式中:Δtp為兩條曲線直接的相位差對應的時間差;q為0或者某一正整數。

第p個故障段導致采集出現了斷裂點,其后的波形被延遲了時間τp。

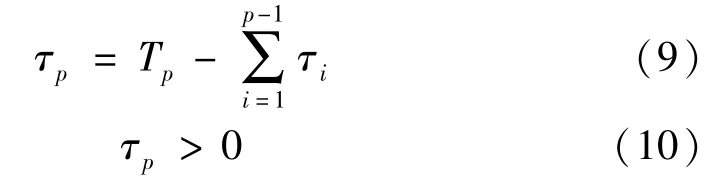
由式(9)、式(10)判定q的取值。

由于采集序列的有限長特征,以及故障發作點在采集序列上出現位置的不可控,導致各個曲線段的長短不一,有些可以用多周期正弦擬合方式進行分析,而另外一些可能需要使用殘周期擬合方式進行分析,這在實際分析過程中需要引起注意。當然,它們的誤差和不確定度也將有很大差異。