鋼框架哺職寮裊η澆峁剮薷春蟮氖褂瞇閱苤副

袁昌魯 李嘉鍇 楊寧

摘要：? 為便于鋼框架-鋼板剪力墻結構震后快速修復，統計既有實驗結果，提出修復后使用的三級性能指標，基于等效拉桿理論，研究結構在側向載荷作用下塑性鉸的出現順序、層間位移角和結構應力發展等情況，并建立有限元模型對指標進行驗證。結果表明：在一級修復性能指標（位移角1/220）下，結構板墻輕微受損，對應的修復方法為對板墻進行輕微修復;在二級修復性能指標（位移角1/110）下，結構板墻幾乎全面進入塑性狀態，需要考慮換板或增加加勁肋修復;在三級修復性能指標（位移角1/85）下，結構板墻已經全部進入屈服狀態，而且框架梁端也出現塑性鉸，此時不僅需要對板墻進行修復，還要考慮對框架進行修復。

關鍵詞：? 鋼板剪力墻; 等效拉桿模型; 層間位移角; 塑性鉸; PUSHOVER分析; 性能指標

中圖分類號：? TU392.4; TB115.1文獻標志碼：? B

收稿日期：? 2021-11-20修回日期：? 2021-12-01

基金項目：? 山東省自然科學基金（ZR2016EEQ27）

作者簡介： 袁昌魯（1987—），男，山東泰安人，博士，講師，研究方向為鋼結構抗震性能，（E-mail）ycl384384@163.com

通信作者： 李嘉鍇（1996—），男，山東濟寧人，碩士研究生，研究方向為鋼結構抗震性能，（E-mail）cangshu1101@163.comService performance index of

steel frame-plate shear wall structure after repair

YUAN Changlu， LI Jiakai， YANG Ning

（School of Civil Engineering， Shandong Jianzhu University， Jinan 250100， China）

Abstract： To facilitate the rapid repair of steel frame-steel plate shear wall structure after earthquake， the three-level performance indexes to the structure repair are put forward according to the statistics of the existing test results. Based on the equivalent tie rod theory， the occurrence sequence of plastic hinges， displacement angle between layers and structural stress development of the structure under lateral load are studied， and the finite element model is established to verify the indexes. The results show that， under the first level repair performance index （displacement angle 1/220）， the structural plate wall is slightly damaged， and the corresponding repair method is to slightly repair the plate wall; under the secondary level repair performance index （displacement angle 1/110）， almost? all of the structural plate wall enters the plastic state， so it is necessary to consider replacing the plate or adding stiffeners for repair; under the third level repair performance index （displacement angle 1/85）， all of the structural plate and wall have? entered the yield， and the plastic hinge also appears at the end of the frame beam， so it is necessary to repair not only the plate and wall， but also the frame.

Key words： steel plate shear wall; equivalent tie rod model; displacement angle between layers; plastic hinge; PUSHOVER analysis; performance indicators

0引言鋼板剪力墻結構是一種高效的側向支撐體系，20世紀70年代，日本的Shin Nittetsu Building[1]開始采用該結構，自此，鋼板剪力墻結構以初始剛度大、延性性能好以及易于修復等優點得到國內外學者的廣泛關注與研究[2]。目前，對于鋼框架-鋼板剪力墻的力學性能和結構設計的研究已相對完善，而對于該結構的震后修復性能指標的研究較少。依據不同的受損程度設置不同的性能指標，有助于在震后選擇符合結構損傷程度的修復方法，便于結構快速恢復功能，防止余震造成更大損失。《建筑抗震設計規范》GB 50011—2010[3]規定“小震不壞、中震可修、大震不倒”的設防標準。該規定其實就是基于性能的抗震設計，建立不壞、可修和不倒3個性能指標。對于“小震不壞”和“大震不倒”這2個性能指標，《鋼板剪力墻技術規程》JGJ/T 380—2015[4]規定非加勁鋼板剪力墻在多遇地震作用下彈性層間位移角不宜大于1/250以及在罕遇地震下彈塑性層間位移角不宜大于1/50，而對于“中震可修”這一性能指標，標準沒有明確位移角限值與之對應。《建筑抗震設計規范》的附錄M表9針對結構豎向構件對應不同破壞狀態的最大層間位移角參考控制目標給出參考數值，其中各結構構件完好、輕微損壞、中等破壞以及不嚴重破壞對應的層間位移角分別為1/300、1/200、1/100和1/55，但該參考控制目標是否可以應用于鋼板剪力墻結構還有待進一步驗證。針對鋼框架-鋼板剪力墻結構震后修復使用這一性能要求，應參考不同的修復方式，根據結構不同的震害現象確立不同層間位移角對應的性能指標。本文使用通用設計與分析軟件SAP2000，基于多拉桿模型[5]，對設計的3種不同高度的鋼框架-鋼板剪力墻結構進行PUSHOVER分析，研究層間位移角和塑性鉸出現的順序，根據不同的層間位移角和塑性鉸出現順序確定不同的性能指標，為該結構體系震后修復方式的選擇提供依據。為查看鋼板剪力墻結構各個部分應力的詳細變化，采用有限元軟件Ansys建立模型計算應力云圖作為對比驗證。Ansys對比模型均選取9層框架的2～3層結構。

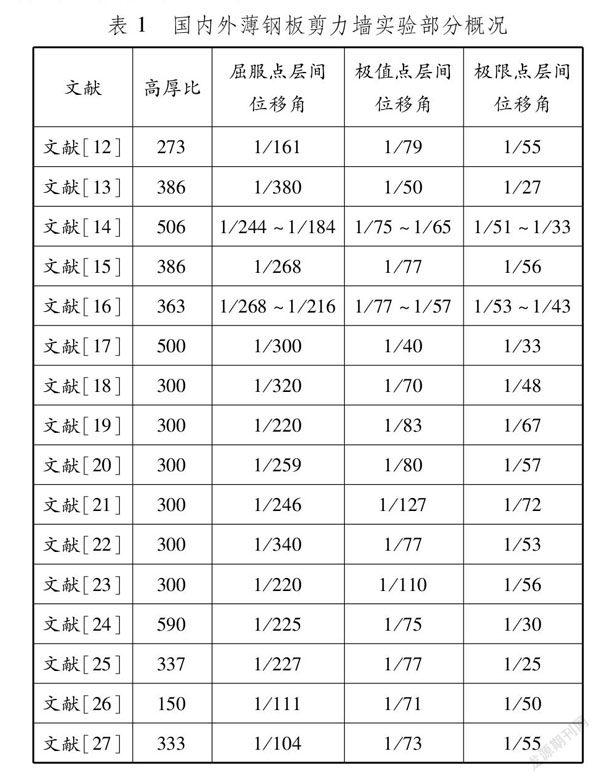
1鋼板剪力墻修復指標確定依據規范中的限制，修復后使用的性能指標對應的層間位移角應在1/250～1/50。鋼板剪力墻結構具有不同的形式，不同形式結構的變形特點也不盡相同，因此在地震作用下會產生不同的破壞模式。針對目前使用較多的薄鋼板剪力墻，統計國內外四邊連接的薄鋼板剪力墻相關實驗，并參考已提出的修復方式[6-11]，建立適用于鋼框架-薄鋼板剪力墻的震后修復性能指標。國內外薄鋼板剪力墻相關實驗數據和實驗結果見表1。

1.1一級修復性能指標一級修復性能指標對應結構受損不嚴重的情況，僅需要對結構中的內嵌板墻進行簡單修復。《建筑抗震設計規范》規定，以鋼結構作為主要抗側力構件的結構，在地震作用下其彈性層間位移角限值為1/250。因此，當結構層間位移角小于1/250時，根據規范規定，結構處于彈性范圍內，結構沒有受到損傷，不需要修復。由文獻資料統計可知，鋼板剪力墻結構彈性層間位移角大多小于1/250，僅個別試驗結構彈性位移角大于1/250。由于構件結構不同，其高厚比越大，內嵌板墻承擔的水平力就越多，導致結構提前進入彈塑性階段。因薄鋼板剪力墻在較小載荷下會出現屈曲，并在對角方向形成斜向的拉力帶，故該修復性能指標允許結構出現一定的面外變形。因為結構進入彈塑性狀態，所以在該修復性能指標下，內嵌板墻中有部分板墻進入屈服階段。該修復標準對應結構輕微受損，因此在此修復性能指標下，框架梁及框架柱須保持在彈性范圍內。在該性能指標下，結構只發生輕微損傷，根據鋼板剪力墻“先板墻、后框架”的破壞模式，此時僅需對內嵌板墻進行簡單修復，結構即可重新投入使用。因此，建議將一級修復性能指標對應的層間位移角限值設定為1/220。

1.2二級修復性能指標二級修復性能指標對應結構受到較為嚴重的損傷，內嵌板墻進入屈服階段以耗散地震力作用下的能量，因此板墻大面積進入塑性狀態。為保證修復結構的經濟性、保證結構的破壞程度是易于修復的，該修復性能指標以板墻大面積進入塑性狀態，而框架梁和框架柱仍基本保持彈性狀態作為主要特征。在該修復性能指標下，雖然內嵌板墻已經大面積進入塑性狀態，但是框架仍保持彈性，因此只需要對內嵌板墻進行修復或者更換，不需要對框架進行修復。綜合已有的實驗結果，建議將該級性能指標對應的層間位移角限值設定為1/110。

1.3三級修復性能指標三級性能指標對應結構受到嚴重的損傷，應保證結構具有可修復性以及修復的經濟性，同時還要防止結構倒塌，保證結構在該修復性能指標下不能超過規范規定的結構在罕遇地震下的彈塑性層間位移角限值，故該性能指標對應的層間位移角不應大于1/50。根據相關實驗統計，鋼板剪力墻結構的極限層間位移角均大于1/61，但此位移角標志結構已經破壞，不具備可修復性或修復的經濟性。為保證結構具有一定的安全裕度，當結構在該修復性能指標位移之前時，應保證結構骨架的應力曲線仍處于上升階段，使結構可以繼續承擔載荷，但在保證結構豎向構件可靠性的情況下，允許部分梁端進入彈塑性范圍。在三級修復性能指標下，結構內嵌板墻已經發生嚴重的破壞，框架也存在一定的損傷，此時修復結構不僅要對內嵌板墻進行修復或者更換，同時要對結構框架進行加固。因此，建議將三級修復后使用性能指標的層間位移角限值設定為1/85。

2算例概況

2.1設計條件算例建筑物縱向為5跨、橫向為3跨，其中帶有鋼板剪力墻部分的跨度為5.4 m，無墻部分的跨度為7.5 m，每層樓的高度均為3.6 m，結構的平面布置見圖1。

假定該建筑所在地的抗震設防烈度為8度（0.2g），場地類別為II類場地、第一組。擬定樓面以及屋面均采用120 mm厚的現澆混凝土樓板，按照折算載荷計算，樓面恒載（含樓板自重）為5.0 kPa，活載取3.0 kPa（含1 kPa的輕質隔墻載荷）;屋面載荷（含樓板自重）為7.0 kPa，活載荷為0.5 kPa。假定標準層外墻的均布載荷為10 kPa，屋面女兒墻的均布載荷取2 kPa。3個算例模型樓層數分別為9層、15層和21層，模型均不考慮縱向地震作用的影響。由圖1可以看出，算例建筑物橫向強度較弱，且橫向抗側力體系為兩榀鋼框架-鋼板剪力墻。由于該結構在橫向和縱向均對稱，可以認為每榀鋼框架-鋼板剪力墻體系承擔整個結構1/2的側向力，通過附加質量的方法，認為每榀框架所承受整個建筑1/2地震力的作用。因結構橫向強度較弱，故選取圖中虛線框內部分為研究對象，3種不同層高的建筑分析模型見圖2。

2.2設計分析模型薄鋼板剪力墻允許內嵌板墻先屈曲后屈服[4]，利用其屈曲后形成的斜向拉力帶可以繼續承擔水平力產生的剪力。因此，在設計中要考慮內嵌板墻屈曲后的性能，但是目前通用的設計軟件，如PKPM、SAP2000以及ETABS等，其殼單元均不能模擬鋼板剪力墻內嵌板墻屈曲后的性能。參考加拿大規范[28]和美國規范[29]，選用其中推薦的拉桿條模型[5]，將板墻離散為一系列傾角為α的斜拉桿，主要考慮內嵌板墻屈曲形成斜向拉力帶后的強度，忽略內嵌板墻的屈曲強度。由最小勢能原理可得到斜拉桿傾角

α=arctan41+twl2Ac1+twh1Ab+h3360lIc??? （1）

式中：tw為墻板的厚度;l為墻板的凈寬;h為墻板的凈高;Ac為邊柱的截面積;Ab為邊梁的截面積;Ic為邊柱的慣性矩。替換內嵌板墻斜拉桿的截面積Asm=lcos α+hsin αntw? （2）式中：n為斜拉桿的數目。根據功的互等定理，內力做功等于外力做功，可以得到鋼板剪力墻的極限承載力Vsm=fytwlsin αcos α（3）式中：fy為鋼板的屈服強度。

2.3截面設計依據《鋼板剪力墻技術規程》的規定以及“強框架、弱板墻”的設計理念，內嵌板墻采用Q235鋼，邊框柱和邊框梁均采用Q345鋼。同時，考慮剪力墻屈曲后產生的斜向拉力帶對柱造成的不利影響，針對有剪力墻跨度的柱，增大其截面以保證結構的整體可靠性。在截面設計時，根據設計條件確定結構在地震載荷作用下所承受的剪力。在內嵌板墻屈服前，鋼板剪力墻結構的內嵌板墻是主要抗側力構件，因此假定所有的剪力完全由內嵌板墻進行承擔，根據式（3）可確定內嵌板墻的厚度，從而根據式（1）確定斜拉桿的傾斜角度α。文獻[5]的研究結果表明，當斜拉桿的數目大于10時可以取得較高的精度，因此模型中假定斜拉桿的數目為12。根據式（2），已知斜拉桿的傾斜角度和數目，可以求得每根斜拉桿的面積。根據以上斜拉桿的參數進行建模試算，若斜拉桿不滿足要求，則通過調整斜拉桿面積反算內嵌板墻厚度，然后通過式（1）確定斜拉桿傾斜角度，建立新模型進行計算。直至斜拉桿滿足要求，確定最終的結構截面尺寸。在對相似截面進行歸一化處理之后，最終得到的9層、15層和21層三跨建筑物的截面尺寸，見表2～4。根據確定的截面尺寸，使用小震反應譜分析對3種算例結構進行檢驗，3種結構在小震反應譜下對應的最大層間位移角依次為1/336、1/337和1/344。3組結構在小震反應譜下的層間位移角小于《建筑抗震設計規范》中的層間位移角限值1/250，滿足要求。

3靜力推覆分析采用SAP2000軟件對算例結構進行PUSHOVER分析，基于拉桿模型采用12根斜拉桿替代板墻。為得到結構的塑性性能，在斜拉桿中定義軸力鉸（P鉸），在框架梁中兩端定義彎矩鉸（M鉸），在框架柱的兩端定義壓彎相關鉸（PMM鉸）。分析選取載荷均勻分布和倒三角分布2種水平加載模式。在修復指標的確定中，采用不同的層間位移角對應不同的修復指標。在算例分析中，計算結構的最大位移角接近或者略大于修復指標時對應的位移角限值，對比結構在該修復指標對應的位移角限值下結構的層間位移角和塑性鉸發展情況是否符合修復目標。在有限元軟件Ansys中建立模型作為對比，查看框架柱和內嵌板墻應力的變化情況。

3.1一級修復性能指標驗證在PUSHOVER分析中，將一級性能指標對應的位移角1/220作為預定目標，對3種結構進行分析。在水平加載的2種加載模式下，結構的層間位移角對比見圖3，結構塑性鉸發展情況見圖4～6，其中塑性鉸B表示屈服點、IO表示立即使用、LS表示生命安全、CP表示防止倒塌、C表示極限強度、D表示殘余強度、E表示結構破壞。在一級修復指標下，3種結構部分樓層的內嵌板墻進入塑性狀態，雖然拉桿模型中的拉桿產生軸力鉸，但該狀態下大多數軸力鉸仍處于關鍵點IO之內，此時結構仍有較多的安全裕度。

一級性能指標下的屈服應力云圖見圖7。在Ansys模型中，此時部分板墻達到屈服應力，仍有部分板墻和框架仍保持彈性狀態，可以繼續吸收能量。因此，在位移角1/220的狀態下，僅需要對板墻進行簡單修復便可以繼續使用，鋼板剪力墻結構滿足該修復指標的要求。

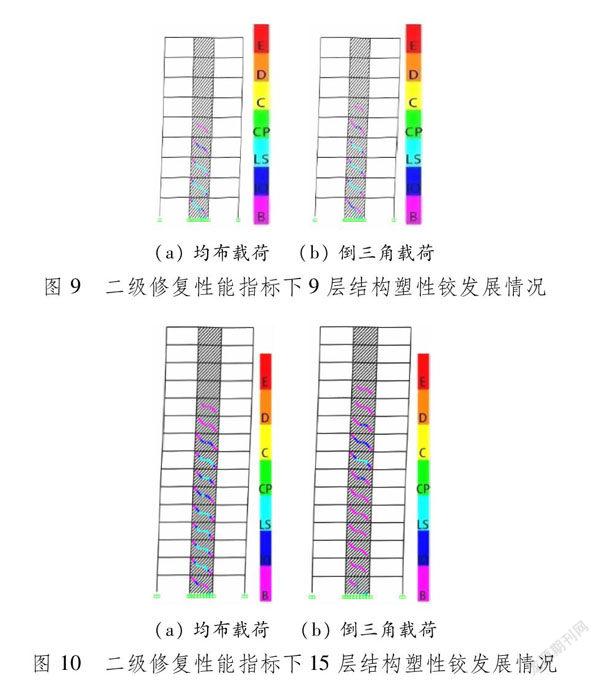
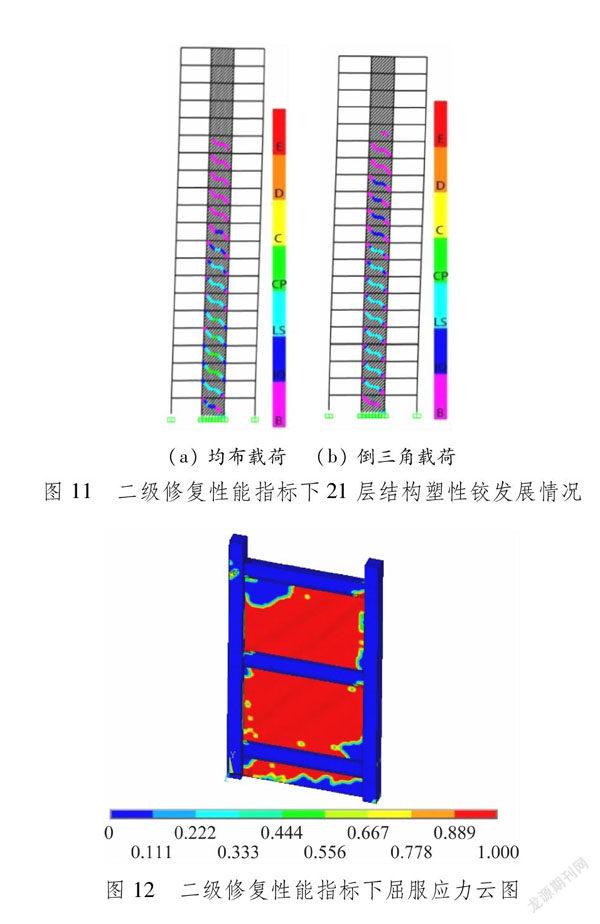
3.2二級修復性能指標驗證以二級修復性能指標對應的層間位移角1/110作為PUSHOVER分析的預定目標，對3種結構進行分析。在水平加載的2種加載模式下，結構的層間位移角對比見圖8。由此可以看出，3種不同結構的最大層間位移角均已大于1/110，滿足限定要求，尤其在15層和21層這個2種較高層建筑中，大多數樓層的層間位移角在1/110附近， 說明較多樓層中的內嵌板墻進入塑性狀態，共同抵抗地震作用。二級修復性能指標下3種結構的塑性鉸發展情況見圖9～11。由此可以看出，較多樓層的拉桿出現軸力鉸，且結構的軸力鉸大多數超過關鍵點IO進入LS，說明內嵌板墻可充分發揮塑性性能。二級修復性能指標下的屈服應力云圖見圖12。在Ansys模型中，此時內嵌板墻幾乎全面進入塑性，但由于板墻塑性的發展，框架除左側加載端外依然保持彈性狀態。此時，結構對應的狀態滿足二級修復性能指標的要求。（a） 9層（b） 15層（c） 21層

3.3三級修復性能指標驗證將位移角1/80為代表的三級修復性能指標作為PUSHOVER分析的預定目標，對結構進行分析，三級修復性能指標下層間位移角對比見圖13。由此可知，斜拉桿大面積出現塑性鉸，此時部分層間位移角較大樓層的兩端也出現塑性鉸，但此時的框架柱沒有出現塑性鉸。三級修復性能指標下3種結構塑性鉸發展情況見圖14～16。

此時，塑性鉸已經進入到關鍵點CP的位置，在材料的角度，板墻已經進入超強階段，如果此時繼續施加載荷，板墻會逐漸退出工作。三級修復指標下對應的Ansys模型屈服應力見圖17，板墻已經全截面進入塑性，加載端梁柱節點域部位幾乎全部進入塑性狀態，底層柱兩側部分應力已經超過彈性范圍，部分梁端也已經進入塑性狀態。此時，對結構進行修復需要考慮對框架進行加強。

4結論（1）通過對已有四邊連接薄鋼板剪力墻結構實驗進行統計，綜合相關規范要求，提出將位移角1/220、1/110和1/85作為三級修復的性能指標。（2）基于等效拉桿模型，利用SAP2000對3種不同高度的三跨鋼框架-鋼板剪力墻結構進行靜力推覆分析和Ansys模型驗證，查看塑性鉸出現的順序和板墻應力的發展情況，三級修復性能指標滿足對應的修復狀態，可以為不同損傷程度的鋼板剪力墻結構修復方法的選擇提供依據。（3）算例計算結果表明，在一級修復性能指標（位移角小于1/220）下，結構板墻輕微受損，對應修復方法只需要對板墻進行輕微修復。結構在二級修復性能指標（位移角小于1/110）下，板墻幾乎全面進入塑性狀態，需要考慮換板或增加加勁肋修復，彌補結構板墻的損傷。結構在三級修復性能指標（位移角小于1/85）下，板墻已經全部進入屈服，而且框架梁端也出現塑性鉸，此時不僅需要對板墻進行修復，還要考慮對框架進行修復。參考文獻：

[1]孫飛飛， 李國強， 張永飛. 薄鋼板剪力墻結構設計的算例研究[C]// 第七屆中日建筑結構技術交流會論文集. 重慶： 中國土木工程學會， 2006： 803-808.

[2]郭彥林， 周明， 董全利， 等. 三類鋼板剪力墻結構試驗研究[J]. 建筑結構學報， 2011， 32（1）： 17-29. DOI： 10.14006/j.jzjgxb.2011.01.002.

[3]建筑抗震設計規范： GB 50011—2010 [S].

[4]中華人民共和國住房和城鄉建設部. 鋼板剪力墻技術規程： JGJ/T 380—2015 [S].

[5]THORBURN L J， MONTGOMERY C J， KULAK G L. Analysis of steel plate shear wall[DB/OL]. （1983-12-30）[2021-11-10]. https：//era.library.ualberta.ca/items/e72bd26b-5136-4e1d-95ee-95e4612511bc. DOI： 10.7939/R3BG2HB64.

[6]QU B， MICHEL B， LIN C H， et al. Testing of full-scale two-story steel plate shear wall with reduced beam section connections and composite floors[J]. Journal of Structural Engineering， 2008， 134（3）： 364.

[7]AMIR R K， TADEH Z， DAVID B， et al. Case study on retrofit of steel plate shear walls using low yield point steel infill plates[J]. Journal of Steel Structures & Construction， 2016， 2（1）： 1-6. DOI： 10.4172/2472-0437.1000106.

[8]呂西林， 毛苑君. 帶有可更換墻腳構件剪力墻的設計方法[J]. 結構工程師， 2012， 28（3）： 12-17. DOI： 10.15935/j.cnki.jggcs.2012.03.015.

[9]紀曉東， 錢稼茹. 震后功能可快速恢復聯肢剪力墻研究[J]. 工程力學， 2015， 32（10）： 1-8.

[10]杜一鵬， 郝際平， 于金光， 等. 鋼板剪力墻結構抗震加固后性能試驗研究[J]. 東南大學學報（自然科學版）， 2019， 49（3）： 420-426. DOI： 10.3969/j.issn.1001-0505.2019.03.002.

[11]杜一鵬， 郝際平， 于金光， 等. 密肋槽鋼修復薄鋼板剪力墻抗震性能研究[J]. 建筑結構學報， 2020， 41（3）： 44-52. DOI： 10.14006/j.jzjgxb.2018.0121.

[12]陳國棟， 郭彥林， 范珍， 等. 鋼板剪力墻低周反復載荷試驗研究[J]. 建筑結構學報， 2004， 25（2）： 19-26.

[13]侯蕾， 孫彤， 郝際平， 等. 十字加勁肋鋼板剪力墻低周反復載荷的試驗研究[J]. 鋼結構， 2006， 21（2）： 12-16.

[14]李峰. 鋼板剪力墻抗震性能的試驗與理論研究[D]. 西安： 西安建筑科技大學， 2011： 25-59.

[15]曹春華. 斜加勁鋼板剪力墻性能研究[D]. 西安： 西安建筑科技大學， 2008： 39-41.

[16]王迎春. 薄鋼板剪力墻在壓彎剪作用下承載力的試驗與理論研究[D]. 西安： 西安建筑科技大學， 2011： 21-22.

[17]周明. 非加勁與防屈曲鋼板剪力墻結構設計方法研究[D]. 北京： 清華大學， 2009： 59-60.

[18]張文強. 半剛接鋼框架-內填非加勁薄鋼板剪力墻體系的試驗研究與理論分析[D]. 西安： 西安建筑科技大學， 2010： 27-29.

[19]虎奇. 半剛性框架-內填十字加勁鋼板剪力墻結構的抗震性能研究[D]. 西安： 西安建筑科技大學， 2011： 27-28.

[20]李巖. 鋼框架-鋼板剪力墻結構體系的試驗研究與理論分析[D]. 西安： 西安建筑科技大學， 2011： 21-23.

[21]郭宏超. 半剛性框架-鋼板剪力墻結構抗震性能研究[D]. 西安： 西安建筑科技大學， 2011： 35-40.

[22]郭宏超， 郝際平， 虎奇， 等. 半剛接鋼框架-十字加勁鋼板剪力墻結構滯回性能研究[J]. 土木工程學報， 2011， 44（10）： 35-44. DOI： 10.15951/j.tmgcxb.2011.10.015.

[23]郭宏超， 郝際平， 李峰. 半剛接框架-斜加勁鋼板剪力墻低周反復載荷試驗研究[J]. 地震工程與工程振動， 2011， 31（1）： 54-60. DOI： 10.13197/j.eeev.2011.01.019.

[24]邵建華， 顧強. 三層鋼框架-薄鋼板剪力墻結構抗震性能試驗[J]. 沈陽建筑大學學報（自然科學版）， 2012， 28（5）： 803-809.

[25]DRIVER R G， KULA D G L， LAURIE K D J， et ak. Cyclic test of four-story steel plate shear wall[J]. Journal of Structural Engineering， 1998， 124（2）： 1-3. DOI： 10.1061/（ASCE）0733-9445（1998）124：2（112）.

[26]CHEN S J， CHYUAN J. Cyclic behavior of low yield point steel shear walls[J]. Thin-Walled Structures， 2006， 44（7）： 730-738. DOI： 10.1016/j.tws.2006.08.002.

[27]牟在根， 楊雨青. 對角槽鋼加勁鋼板剪力墻抗震性能試驗研究[J]. 工程力學， 2021， 38（3）： 214-227.

[28]Canadian Standards Association. Limit states design of steel structures： CAN/CSA S16-01[S].

[29]Seismic evaluation and retrofit of existing concrete buildings： ATC-40[S]. （編輯武曉英）