一種高效的自監督元遷移小樣本學習算法

史家輝，郝小慧，李雁妮

(西安電子科技大學 智能媒體與數據工程研究所，陜西 西安 710071)

近年來深度神經網絡已經在監督識別任務上取得了令人振奮的突破，例如視覺[1]、語音[2]、自然語言處理[3]等各個不同的應用領域。然而，深度學習是一種數據饑渴的技術，它取得的出色性能依賴于大量帶類標簽的訓練樣本。但現實的很多應用領域沒有足夠的有類標簽的訓練[4]，或者獲得類標簽樣本的成本非常高。例如醫療[5]、安全[6]等領域。因此，當前深度學習有一個瓶頸問題即小樣本問題[7-8]。人類有一種很強的能力，即從少量的可用樣本中可以識別新類。受此啟發，從少量樣本中學習到一個健壯的模型，這樣的一個任務稱為小樣本學習[9]。

隨著深度學習技術的發展，小樣本學習領域涌現出一些優秀的算法。目前小樣本學習方法主要有基于數據增強、基于元學習、基于遷移學習以及混合的方法。深度學習小樣本問題的本質是訓練過程中的監督樣本過少而很難擬合模型中大量的參數，導致其精度很低。然而，現有的普通數據增強方法只能緩解而不能解決小樣本問題，利用生成網絡進行數據增強，由于先驗知識的不完美，生成的數據與真實數據之間的差異會導致概念偏移。因此如何利用模型從數據本身中充分挖掘其信息是解決小樣本問題的關鍵。相比較而言，混合方法最為有效。基于元學習的方法[10-14]利用以往的經驗知識來指導新任務的學習，具體來說就是在元學習階段將數據集分解為不同的元任務，去學習類別變化情況下模型的泛化能力，在元測試階段，面對新任務(新的類別)，不需要變動已有的模型就可以完成分類。基于遷移學習的算法[15-20]利用從源域任務中提取的有用知識來解決目標任務；一種典型的方式就是微調，得到一個已經訓練好的基礎網絡后，使用小樣本數據集進行迭代次數很少的訓練就可以用于測試。混合型算法[21-23]能夠結合不同技術的優點而顯著提升算法的性能。基于元學習和遷移學習的混合算法最具代表性。綜上所述，現有小樣本算法主要存在以下缺陷：(1)算法模型提取的特征有限，缺乏對不同尺寸特征的挖掘，及對重要特性的關注度；(2)模型的泛化能力弱。在遷移學習預訓練階段得到基礎網絡的過程中，如果使用的數據集和新類的數據集的分布差異大，則對新類的分類效果就會很差。

為克服已有算法的上述缺陷，筆者提出了一種高效的自監督元遷移小樣本學習算法：(1)提出了一種新的殘差注意力膨脹網絡，通過膨脹分支使模型增大了感受野，可以提取不同尺寸的圖像特征，并且殘差注意力增強了對重要特征的關注度；(2)提出了基于自監督的預訓練策略，在遷移學習通過預訓練方式獲取基礎網絡的過程中，使用自監督方式，通過對圖像數據進行旋轉，建立了關于圖像結構信息的標簽，對圖像本身的結構信息進行了充分挖掘，增加了訓練任務中的監督信息，增強了模型的泛化能力；(3)一種高效的自監督元遷移小樣本學習算法(Efficient Self-Supervised Meta Transfer algorithm for few shot Learning，ESS-MTL)，在基準小樣本數據集上，以當前最具代表性的若干優良的小樣本算法作為算法性能比較的基準算法。大量的實驗結果表明：所提算法正確高效，性能優于所有的基準算法。

1 相關工作

目前，大多數小樣本算法主要集中在元學習以及遷移學習的混合型小樣本學習算法方面。FINN等提出的與模型無關的元學習[12]算法(MAML)是最為經典的元學習算法，其他元學習算法和混合型算法都是建立在此算法的基礎上的。在預訓練階段對模型在大量不同任務上訓練模型參數，使得學習到的模型參數只要經過少量次數的梯度更新就能實現在新任務上的快速學習。但MAML算法需要大量的不同任務，代價高，而且過擬合問題嚴重。ANTONIOU[13]等提出的MAML++算法是對MAML算法的改進，改善了MAML的泛化誤差，穩定和加快了MAML算法的訓練過程。但該算法依然未能解決MAML算法的上述問題。為了克服元學習算法的過擬合問題，ORESHKIN[14]等提出一種基于度量的元學習算法TADAM，TADAM算法通過輔助任務協同訓練以根據特定任務調整特征提取器，使得度量空間與任務相關，在這種情況下的特征提取器具有良好的泛化能力。

一些基于遷移學習的算法使用預訓練權重進行初始化的思想，并針對特定任務進行微調[17-20]。MTL[21]是一個將元學習和遷移學習結合來完成圖片分類任務的算法。該算法一共分為兩個階段：預訓練階段和元學習階段。首先在預訓練階段在大量帶標簽的數據集上訓練好一個基礎網絡，然后使用遷移學習微調的方法遷移該基礎網絡，之后在小樣本數據集上進行元學習。由于基礎網絡的參數量很大，直接進行微調可能會增加過擬合風險，因而該算法在微調階段設計了一種方法減少了要微調的參數量。首先在大規模數據上預訓練獲得良好的初始權重，然后將其“凍結”(如圖1淺色部分所示)，針對小樣本學習場景利用元學習的兩個輕量級神經元操作縮放與移位(Scaling and Shifting，SS)，給每個“凍結”的卷積核添加兩個縮放與移位參數φS1和φS2(如圖1深色部分)，去適應新的小樣本學習任務。

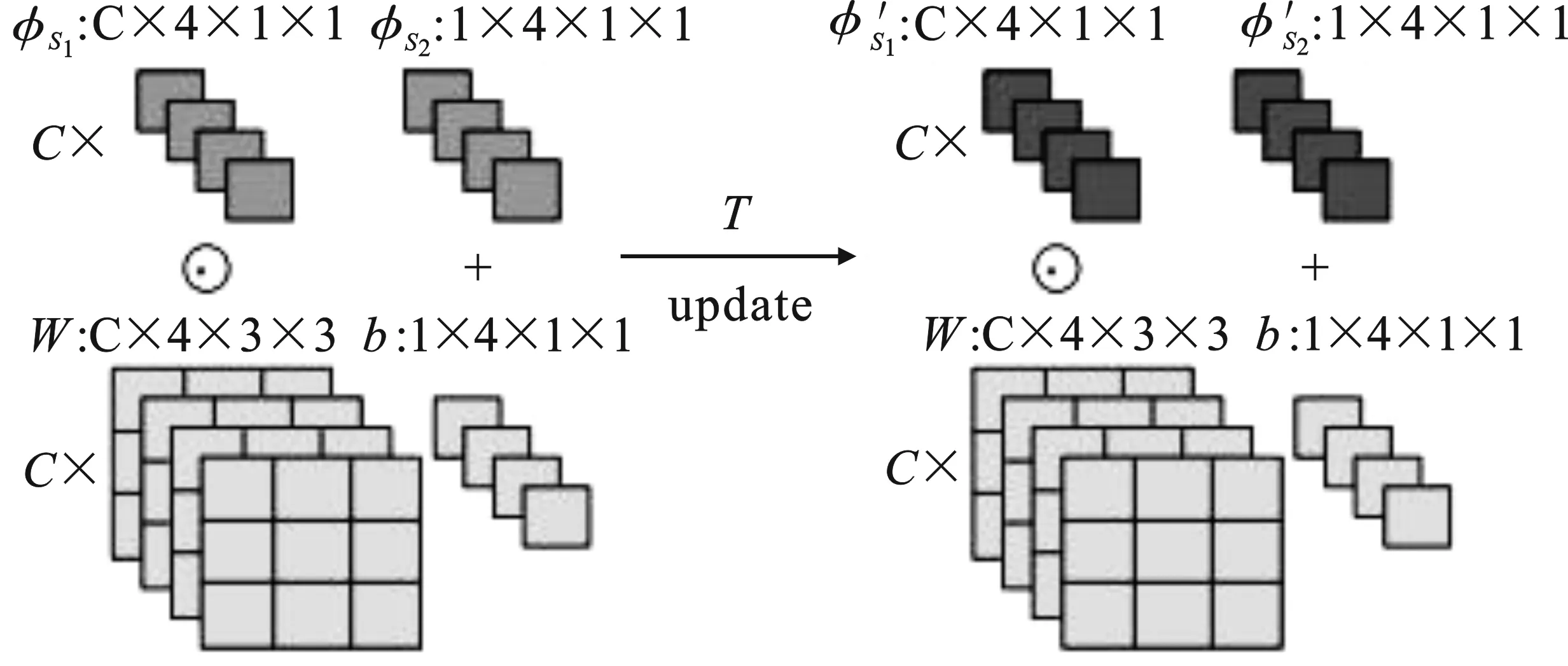
圖1 縮放和移位示意圖

針對小樣本學習場景，模型不再需要更新所有參數(如圖1淺色部分)，而只需要更新添加的兩個縮放與移位參數φS1和φS2。SS操作如式(1)所示，其中，FSS(·)是SS操作的函數表示，X是輸入，?表示逐元素相乘，φS1和φS2分別表示縮放和移位參數。MTL算法雖然減少了需要更新的參數量，降低了過擬合風險，但精度不夠高。

FSS(X；W，b；φS{1，2})=(W?φS1)X+(b+φS2) 。

(1)

TransMatch[22]是YU等于2020年提出的一種新的混合型小樣本學習算法。該算法將遷移學習與半監督學習相結合，以充分利用來自有標簽的基類數據和無標簽的新穎類數據的輔助信息。但是TransMatch采取微調的策略進行權重的遷移，微調策略所需要調試的參數量過大，容易產生過擬合。受MAML算法的啟發，LIAN等[23]提出了T-NAS算法，針對小樣本學習場景，T-NAS創新性地將元學習的思想與神經體系結構搜索相結合，提出了一種新穎的可遷移神經體系結構搜索方法，但是相對于目前最新的小樣本學習算法，T-NAS算法的精度不夠高。PATACCHIOLA等[27]提出了一種基于深度內核學習的高度靈活的貝葉斯模型，并得出元學習可以用簡單的分層貝葉斯模型代替，而不會損失準確性的結論。WANG等[25]對元學習的基本機制以及使用元學習訓練的模型與經典訓練的模型之間的差異進行了深入的研究并開發了一種正則化程序，可提高針對小樣本分類的標準訓練例程的性能。但精度不夠高。

盡管當前一些最新小樣本算法已取得了SATA(State-of-the-Art)性能結果，但其過擬合能力與算法精度仍有待于進一步提升。現有小樣本算法大部分都是基于算法層面提高算法在小樣本情境下的分類精度，而筆者提出的ESS-MTL算法是基于數據特征層面的，即基于從有限的少量樣本中挖掘更多重要特征的思想。

2 ESS-MTL算法

首先概述所提出的ESS-MTL算法的網絡模型；其次詳細論述筆者所提出的一種新的特征器網絡，即殘差注意力膨脹網絡；最后介紹所提出的基于自監督的預訓練算法。

2.1 ESS-MTL深度網絡模型

ESS-MTL算法的網絡模型如圖2所示，它由特征提取器和分類器兩個模塊構成，各模塊的功能如下：

(1)特征提取器：設計了一種殘差注意力膨脹網絡作為特征提取器，如圖2中下方虛線框所示。膨脹分支的設計使得網絡能夠提取不同尺寸的特征，殘差注意力能夠增強模型對于重要特征的關注度。其中D2-Conv3×3表示添加了膨脹卷積的膨脹分支。

(2)分類器：采用一個全連接層FC-classification與Softmax層作為類別分類器，全連接層對特征提取器的輸出進行處理，并采用Softmax對輸出進行歸一化處理，從而獲得輸入數據屬于每個類別的概率。為了緩解小樣本學習算法中過擬合的問題，采用添加L2正則化項的交叉熵損失函數作為ESS-MTL網絡模型的目標函數。

值得注意的是：圖2中分類器中上方虛線框所示為筆者提出基于自監督的預訓練算法中使用的自監督分類器來使得模型對數據本身的結構信息充分挖掘，提高模型的泛化能力。

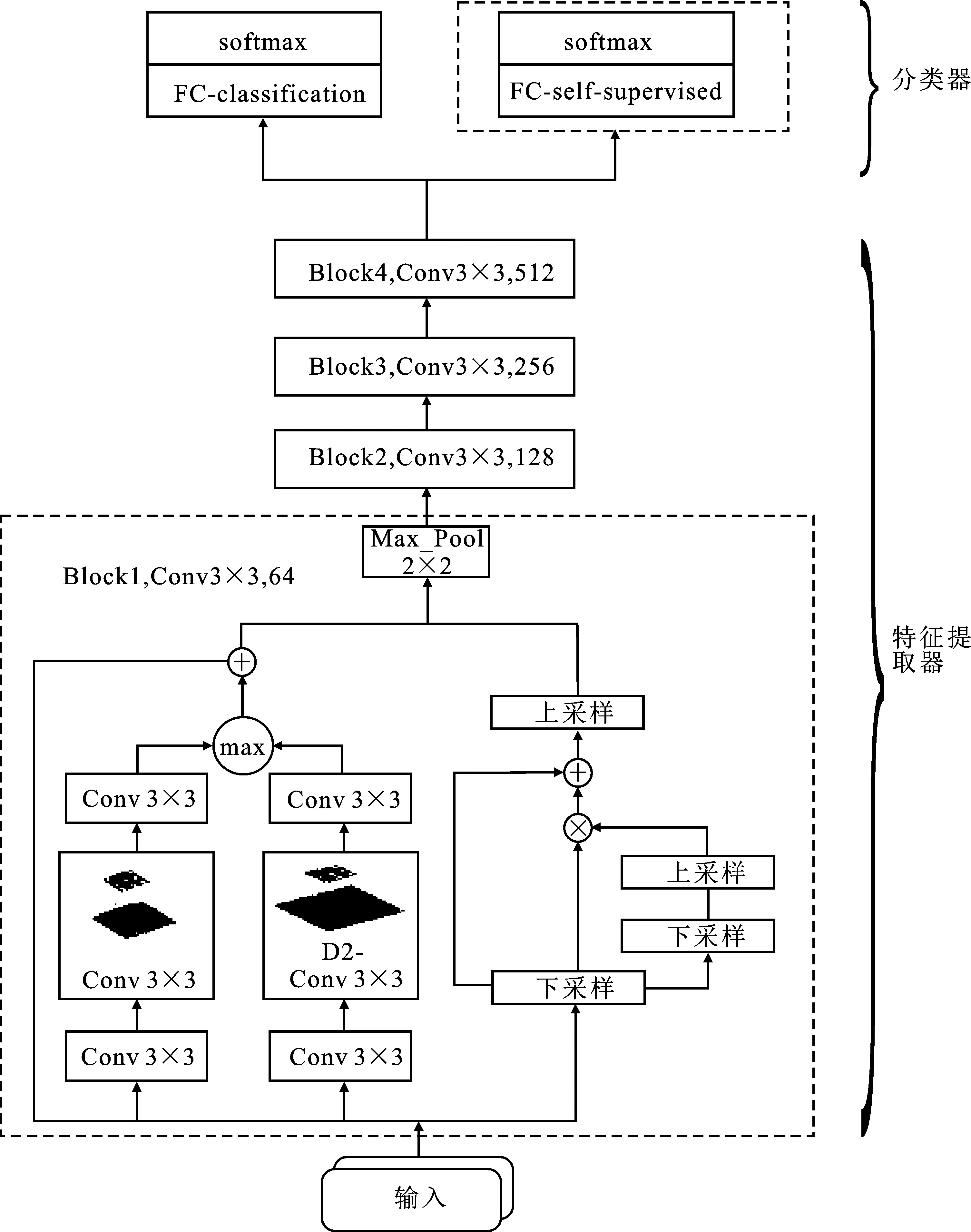
圖2 ESS-MTL算法模型結構示意圖

2.2 殘差注意力膨脹網絡

傳統卷積網絡使用固定尺寸的卷積核，只能挖掘固定尺寸的特征，而且對圖像中的所有特征做同樣的處理，缺乏對重要特征的關注，因此提取的特征有限。針對上述缺陷，提出了殘差注意力膨脹網絡。首先，基于傳統的卷積網絡，添加了采用擴大卷積核采樣間隔的卷積過程，此處將這一過程稱為膨脹卷積，它不僅擴大了網絡的感受野，而且可以提取不同尺寸的特征。其次，將添加了膨脹卷積的卷積網絡稱為膨脹卷積網絡，將所提出的一種適合圖片的注意力機制稱為殘差注意力，基于膨脹卷積網絡添加殘差注意力，網絡增強了對重要特征的關注度。最后，將最終的改進網絡稱為殘差注意力膨脹網絡。

2.2.1 膨脹卷積網絡

使用目前比較流行的ResNet 12[26]網絡作為特征提取器。ResNet 12是基于卷積的一種深度網絡模型，但它只能獲得固定尺寸的特征，感受野受限。對其添加膨脹卷積分支，不僅可以擴大網絡的感受野而且可以提取不同尺寸的特征。此處將該網絡稱為膨脹卷積網絡。

通常增大卷積網絡模型感受視野的方法有兩種：一是增大卷積核尺寸，二是增大卷積核相鄰兩步間隔dp。其中，dp也稱為膨脹系數。固定的卷積核尺寸只能獲取固定尺寸的特征，過大的卷積核尺寸無法捕獲局部細膩特征，因此通過增大卷積間隔來擴大視野。傳統卷積與膨脹系數為2的膨脹卷積對比如圖3所示，左圖為傳統卷積，右圖為膨脹卷積且dp為2。

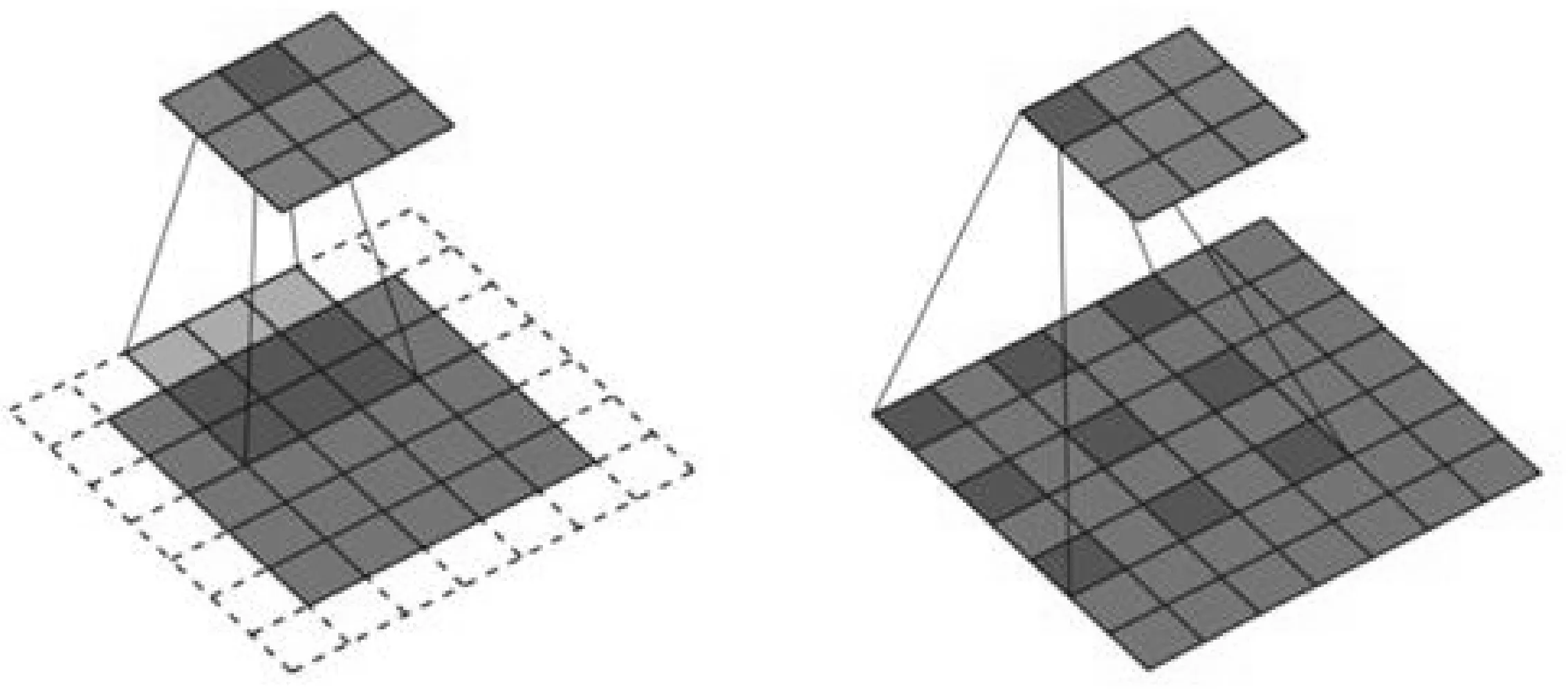
圖3 傳統卷積與膨脹卷積網絡示意圖

基于Resnet12模型結構，在特征提取器的每一個殘差塊(Block)添加了膨脹卷積分支。該特征提取器網絡中共包括4個殘差塊(Block)，其中Conv3×3代表每個殘差塊中卷積核尺寸為3×3，用C表示。每個殘差塊中卷積核個數分別為：64，128，256和512。4個殘差塊的結構相同，只是卷積核個數不同。為了便于描述，用Num表示各個殘差塊中的卷積核個數。改進前的ResNet 12網絡模型中每個殘差塊的結構如圖4(a)所示。筆者提出的膨脹殘差注意力網絡的殘差塊如圖4(b)所示，在原來網絡模型的基礎上，添加一個膨脹卷積分支，A2-Conv3×3表示膨脹系數為2的卷積操作，用CA2表示，Max_Pool表示最大池化操作，用P表示。

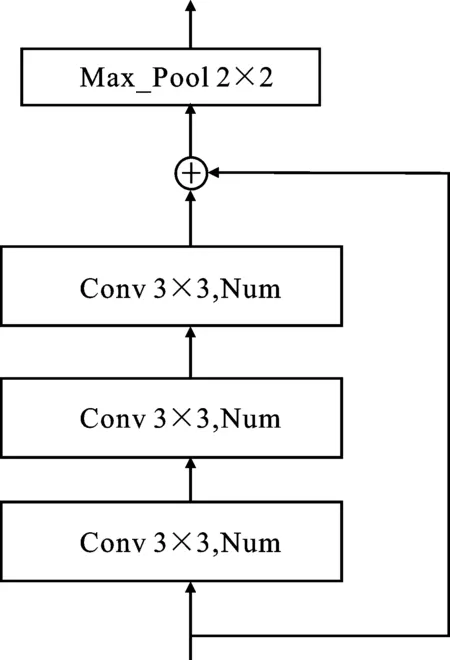
(a)改進前的殘差塊示意圖

圖中，每個Block的輸出Xi分別如下所示：

Xi=C(Xi-1)+Xi-1，

(2)

Xi=P(max(Xi-left，Xi-right)) ，

(3)

其中，Xi-1表示上一個Block的輸出，Xi-left表示改進后的Block左分支的輸出，Xi-right表示右分支的輸出，max(·)表示矩陣元素級別取最大操作，P表示最大池化函數。分別計算Xi-left和Xi-right：

Xi-left=C(Xi-1)+Xi-1，Xi-right=CA2(Xi-1)+Xi-1，

(4)

其中，膨脹卷積分支能捕獲更大尺寸特征，且每個分支獨立更新自己的縮放與移位參數，進一步增強了模型的適應性。

2.2.2 殘差注意力機制

筆者提出了一種適合視覺任務的注意力機制，稱為殘差注意力。基于上一節提出的膨脹卷積網絡添加殘差注意力，增強了模型對重要特征的關注度，提高了模型提取數據特征的能力。在每個Block中添加了殘差注意力機制，如圖5所示。

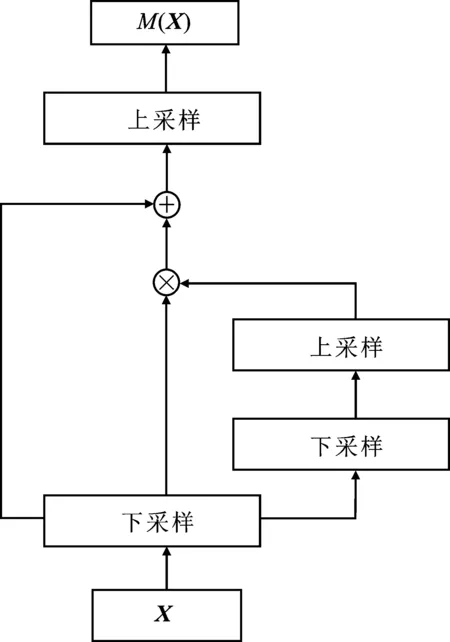
圖5 殘差注意力機制示意圖

筆者所提出的殘差注意力機制所得注意力向量的計算方式如下所示，

Mi(Xi-1)=D(Xi-1)+D(Xi-1)?U(D(D(Xi-1))) ，

(5)

其中，Mi(Xi-1)表示當前Block的注意力向量，D(·)表示下采樣操作，采用最大池化方法，U(·)表示上采樣操作，上采樣則采用雙線性插值法。因此，添加注意力機制的每個Block最終的輸出如下所示，

Xi=Xi+Xi?Mi(Xi-1) 。

(6)

最大池化即只取對應位置的最大值，并且不經過反向傳播的修改，池化層對特征進行壓縮時只是過濾掉無關的信息，而留下來的信息則具有尺度不變性的特征，充分表達了圖像內容的特征，這一過程加強了重要的特征。另外，對獲得的重要特征進行雙線性插值能使得原來不重要特征產生退化，這一過程減弱了不重要的特征。通過兩次上采樣與下采樣的操作，模型更加突出了重要的特征而抑制了不重要的特征。將最終的改進網絡稱為殘差注意力卷積網絡。它不僅提高了模型的感受野，可以提取不同尺寸的特征，而且增強了模型對重要特征的關注度，提高了模型對數據特征的提取能力。

2.3 基于自監督的預訓練算法

在遷移學習預訓練階段得到基礎網絡的過程中，如果使用的訓練數據集和新類的數據集的分布差異大，對新類的分類效果就會很差，即模型的泛化能力弱。針對該問題，筆者提出了基于自監督的預訓練算法，在預訓練階段，使用自監督的方式通過對圖像數據進行旋轉，建立了關于圖像結構信息的標簽，對圖像本身的結構信息進行了充分挖掘，增加了訓練任務中的監督信息，增強了模型的泛化能力。

ESS-MTL算法的整個過程分為兩個階段：預訓練階段和元學習階段。自監督主要是利用輔助任務從大規模的無監督數據中挖掘自身的監督信息，通過這種構造的監督信息對網絡進行訓練，從而可以學習到豐富的、通用的對下游任務有價值的表征。筆者提出的基于自監督輔助任務的預訓練算法如圖6所示。

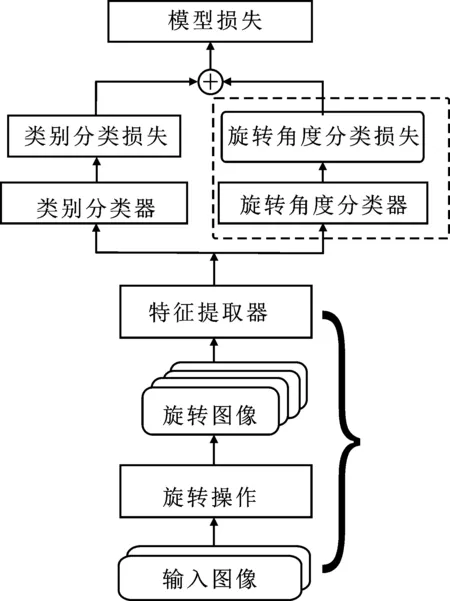
圖6 基于自監督(虛框標注)的預訓練示意圖

如圖6所示，筆者提出了一種基于旋轉的自監督預訓練算法。對于每一個批次的圖片分別進行0°、90°、180°、270°旋轉，并將旋轉角度作為監督信息建立圖像旋轉角度標簽，從而獲得更多的監督信息。由此，本文構建了一個旋轉角度分類器，旋轉角度分類損失與標準類別分類損失作為最終的損失函數對模型進行預訓練。

在本階段，首先隨機初始化特征提取器Θ，傳統類別分類器θ以及自監督輔助任務的旋轉角度分類器θss，然后通過梯度下降法對其進行優化：

[Θ，θ，θss]=[Θ，θ，θss]-α?LD([Θ，θ，θss]) ，

(7)

其中，LD代表損失函數，此處采用添加交叉熵損失函數，α代表學習率。采取了添加自監督輔助任務的預訓練方式，因此LD包含傳統的分類損失與旋轉角度分類損失，具體計算方式如下所示：

LD=λLClassification+(1-λ)LSelf-supervised，

(8)

其中，λ代表類別分類損失與旋轉分類損失之間的平衡參數，在本文的實驗中選取為0.7。λ的選取范圍為0.6到0.9。若小于0.6，分類效果下降，此時特征提取器注重學習圖片本身信息，不是分類信息。在預訓練階段主要學習特征提取器Θ。分類器θ以及θss將被丟棄，因為隨后的小樣本學習任務包含不同的分類目標，例如5-way-1-shot的分類是5個類別而不是預訓練階段的64類，且在元學習階段沒有添加關于旋轉的自監督分類目標。

3 實驗結果

在兩個標準數據集上對ESS-MTL算法進行實驗，并與其他最新最好的小樣本學習算法進行比較。對算法的實驗數據集，實驗參數設置及衡量指標，對比實驗和消融實驗及其結果分析進行了介紹。

3.1 實驗數據集

針對兩個小樣本標準數據集miniImageNet和Fewshot-CIFAR100(FC100)進行實驗。miniImageNet數據集由Vinyals等人于2016年提出，用于小樣本學習算法的評估，miniImageNet節選了ImageNet數據集中100個類別，每個類別包含600個84×84彩色圖像樣本。這100個類別中有64個類別用于元訓練，16個類別用于元驗證，20個類別用于元測試的采樣任務。

Fewshot-CIFAR100(FC100)數據集是基于流行的對象分類數據集CIFAR100構建的。它提供了更具挑戰性的方案，它具有較低的圖像分辨率和更具挑戰性的元訓練/測試劃分。它包含100個對象類，每個類有600個32×32彩色圖像樣本。這100個類別屬于20個超類。元訓練數據來自屬于12個超類的60個類，元驗證和元測試集分別包含20個類，分別屬于4個超類。這些劃分是基于超類的，從而最大程度地減少了訓練和驗證以及測試任務之間的信息重疊。

3.2 實驗參數設置及衡量指標

筆者提出的ESS-MTL算法所使用的超參數如下：預訓練階段迭代次數為20 000次，預訓練階段學習率為0.001，元訓練階段次數為20 000次，元學習率為0.001，基礎學習率為0.001。

基于miniImageNet數據集進行了兩種分類實驗的設置：即5-way-1-shot和5-way-5-shot；基于FC100數據集進行了3種分類實驗設置：即5-way-1-shot、5-way-5-shot和5-way-10-shot。N-way-K-shot表示每一個測試批次都有N個未出現在訓練集中的類別，每個類別有K個樣本。遵循規范，筆者用準確率FAcc作為實驗性能評價指標，

(9)

其中，Ncorrect表示預測正確的樣本數量，Ntotal表示總的樣本數量。

3.3 算法性能比較及分析

對筆者提出的ESS-MTL算法與目前最好的小樣本學習算法在標準測試數據集miniImageNet和FC100上進行了算法性能比較實驗。實驗結果如表1所示。

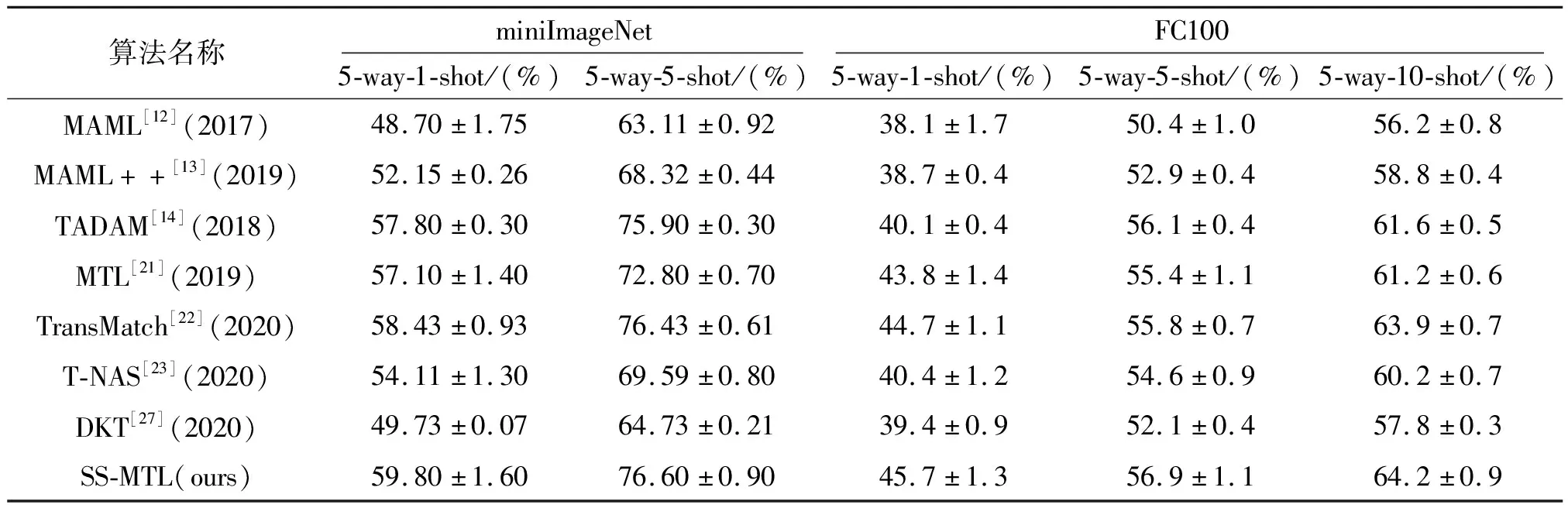
表1 ESS-MTL算法與對比算法在miniImageNet和FC100上的精度對比表

筆者提出的ESS-MTL算法在兩個實驗數據集上不同實驗設置下均優于目前最新的小樣本學習算法，充分驗證了筆者提出算法的有效性。本文提出的ESS-MTL算法相較于前人的算法精度明顯提升，特別是在miniImageNet數據集上。這是因為miniImageNet數據集中的圖像尺寸相對于FC100數據集比較大，通過膨脹卷積分支增大了模型的感受野。所以對于固定尺寸的卷積核，尺寸較大的圖像能挖掘其更多大尺寸的特征，針對于算法精度的提升更為顯著。

3.4 消融實驗及分析

為了進一步驗證筆者所提出上述模型或方法的有效性，分別基于2分類自監督輔助任務與4分類自監督輔助任務，以及未添加自監督輔助任務的算法進行了消融實驗。實驗結果如表2所示。

表2 自監督輔助任務實驗精度對比表

表2中，2-SS-Pretrain(2-Self Supervised-Pretrain)表示添加2分類自監督輔助任務的MTL算法，分別對輸入圖像進行0°、180°旋轉；4-SS-Pretrain(4-Self Supervised-Pretrain)表示添加4分類自監督輔助任務的MTL算法，分別對輸入圖像進行0°、90°、180°和270°旋轉。Meta-Tr代表在元訓練階段的分類精度，Meta-Te表示在元測試階段的分類精度。上述實驗結果表明：(1)相比于傳統的預訓練方法，添加自監督輔助任務的預訓練不僅在預訓練的過程中取得較好的精度，在元遷移學習階段也能取得具有競爭力的結果，充分說明添加自監督輔助任務的有效性；(2)由于構造了更多的監督信息，相對于2分類自監督，4分類自監督輔助任務對于算法性能提高取得的效果更為顯著；(3)預訓練階段自監督輔助任務的添加對于算法的精度有了進一步的提升，并且是在保持原始需要優化的參數量的情況下。

4 結束語

針對現有小樣本學習算法存在的缺陷，首先，對視覺任務中常使用的傳統卷積網絡(Resnet12)提取特征有限的問題提出殘差注意力膨脹卷積網絡作為特征提取器，能夠提取不同尺寸的特征而且增強了對重要特征的關注度；其次，針對模型的泛化能力弱在遷移學習通過預訓練的方式獲取基礎網絡的過程中提出了基于自監督的預訓練算法，對數據本身的信息進行挖掘，提高算法的泛化能力；最后，將本文提出的算法與目前最新的小樣本學習算法在基準數據集miniImageNet以及FC100上進行對比實驗，通過實驗證明了筆者所提出策略的有效性以及本文算法相對于目前比較優秀的算法的優越性。

然而小樣本學習的算法的精度相對于傳統算法的精度仍不夠高，因此，進一步提高小樣本學習算法的精度是今后的目標。