卸荷作用下巖質邊坡開挖穩定性的數值研究

丁 欣

（濟寧市水利工程施工公司,山東 濟寧 272100）

1 引言

邊坡穩定性的問題研究一直都是巖土工程領域關注的熱點與難點。眾多學者在巖質邊坡的研究中主要研究分析方法主要有以下六大類：結構分析法、經驗類比法、概率分析法、極限平衡法、地質分析法及數值分析法[1]。隨著計算機科學在土木工程中應用逐漸廣泛,目前的主要研究方法為極限平衡法和數值分析法。

在極限平衡法的研究中,邱煥峰等[2]采用有限單元法（FEM）提出了一套完善的邊坡穩定性分析系統及評價體系。極限平衡法由于有著物理意義明確和計算簡單的優勢被實際工程廣泛的運用。但極限平衡法引用了過多的簡化與假設,與實際工程中巖體邊坡開挖的應力應變差距較大,因而在使用條件上有很大的局限性。數值分析法不僅可以研究傳統方法不能研究的邊坡破壞過程中的發展進程,還可以協調巖體與支擋構造的一致變形,因而利用數值分析法進行巖石邊坡開挖過程中的穩定性研究。胡建華等[3]采用卸荷巖體力學理論方法使得開挖過程中卸荷巖體力學的參數計算模擬的計算流程進一步確立。徐平等[4]使用試驗的方式,基于邊坡巖體開挖卸荷帶及其參數研究分析了邊坡進行了施工開挖卸荷效應的流變穩定性。在此基礎上,梁霄等[5]采用通用有限元模擬巖體、結構面的非線性力學性狀采用接觸單元的方式模擬、邊坡開挖卸荷過程利用單元生死的特性來模擬。結果分析：數值模擬結果與現場實驗結果基本吻合。黃達等[6]通過對裂隙巖體進行物理模型試驗來研究分析卸荷狀態時應力路徑下巖體的強度、變形以及變形破壞特征,并就裂隙的力學機制以及其擴展演化的過程進行研究分析。胡海浪[7]使用卸荷巖體力學和開挖過程的彈塑性變形理論方法對邊坡開挖中卸荷效應的相關問題進行數值和理論分析。

前人運用數值分析方法主要集中在巖體開挖的穩定性卸荷[8]的過程中,而沒有進一步應用于水利工程中。鑒于此,本文擬以金佛山水庫實際工程應用背景出發,研究在卸荷效應作用下巖質邊坡的開挖穩定性。

2 工程概況

某水庫壩址區位于深切中山地貌的環境下。河道是一條長度411 m、流向為西偏北68°方向,河流陡坡為1.1%的較為順直的河道。為左陡右緩的河流形態,呈現出兩端對齊的的U型河谷,正常蓄水位836 m對應河谷的寬度為313 m。河流左側為高 120 m～140 m的基巖陡崖。其中坡度約60°主要分布于775 m高程以下,坡度約70°主要分布于755 m～885 m高程,坡度約36°主要分布于840 m～920 m高程,755 m～885 m高程坡度約80°,而840 m～920 m高程坡度約38°,900 m以上高程地形則相對較為平緩。

3 模型介紹

3.1 有限元模型

建模主要依據于南川金佛山水利工程地質平面圖,對圖1中的1-1截面建立模型,由于 1-1 剖面穿過了兩條較大的裂隙（X1和X2兩條裂隙）,是相對較為不好的地質條件,對此建立模型可以解決此工程中較為普遍的問題；1-1截面位于鉆孔取樣檢測較為廣泛的壩址左壩肩,同時擁有豐富的地質資料,作為分析大壩的安全性與穩定性的研究,1-1截面能夠提供很好的參考意義。建立的模型見圖1。模型高度為151 m,該標準依據左岸邊坡坡頂高度。并向兩側下方延伸,其兩側延伸長度為坡高的5 倍,下方的延伸長度為坡高的4 倍。因此,這一舉措減少了邊界約束對坡體的影響,還能夠較為真實地反映出坡體在力的作用下的變形。

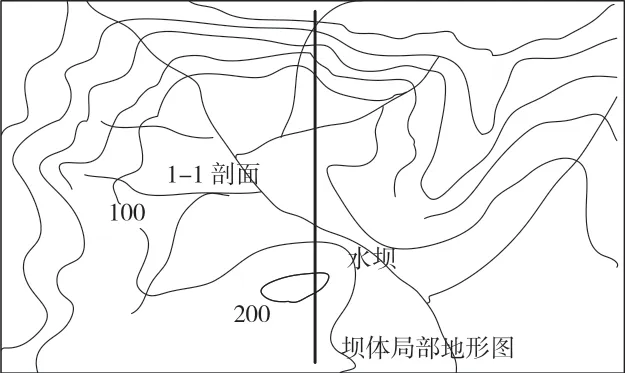
圖1 滲流穩定性計算成果

圖2 開挖剖面幾何模型

由勘察報告的結果所知,對于本次模擬,主要構建三層地質巖層,最上層為頁巖、中層為粉砂巖、最下層為頁巖；從坡面至坡內依次劃分為強卸荷帶巖層、弱卸荷帶巖層、基巖巖層。開挖坡面的幾何模型見圖3。

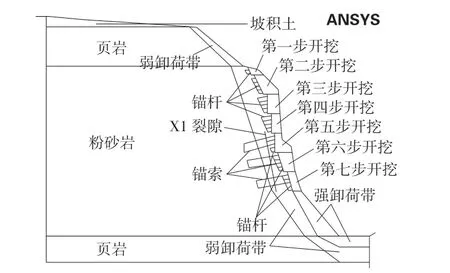
圖3 開挖坡面幾何模型

3.2 單元及網格劃分

采用有限元軟件ANSYS建立了數值模型。巖體破壞的屈服準則依據的是破壞準則。在反映巖體抗拉強度小、抗壓強度大等方面,該破壞準則具有很大的優勢。

該模型的單元擬采用以下方法進行選取：構建PLANE82 （具有8 個節點的四邊形單元）巖體單元,對于模擬曲線邊界的模型具有很好的適用性。同時構建了錨桿單元,X1 和X2 裂隙采用了空單元進行模擬。本開挖坡面模型數值模擬計算共有36412 個單元,其中在左岸邊坡分布有24304 個單元,剩余的單元全部分布在距離研究對象450 m的范圍內。單元選取的過程中遵循以下原則：在開挖巖體的范圍內,巖體、X1 和X2 裂隙采用較密的單元進行劃分。非研究對象的單元網格按距離為梯度依次增大單元體間隙。由以上原則劃分的單元體由于開挖范圍內單元劃分較為密集,在單元網格圖中顯示為顏色較深的區域,有限元網格圖見圖4。

圖4 有限元單元網格圖

3.3 不同工況下模型的建立

為了使模擬的結果更加符合邊坡開挖的實際過程,從而分析該水庫邊坡開挖的穩定性,本模型按照與實際工程開挖相符的由上而下逐層開挖、逐層支護的動態模擬過程進行模擬,設計了幾組不同的計算工況見表1。

表1 計算工況方案設計

通過對比各組模擬結果,擬比較分析以下待解決的問題：

通過對第一、二組模型的計算分析,可以比較分析現有設計方案的經濟性、合理性。比較分析不同施工方案的作用效果,判斷得出多余的處理措施以及尋找待加強的工程防護,使得工程在安全性的基礎上,經濟性達到最優。

通過對第三、四組模型的計算分析,擬探究開挖卸荷作用對邊坡開挖過程中的的變形量影響,進而分析就其對巖體邊坡的穩定性影響進行分析。依此驗證邊坡開挖模型考慮卸荷效應的影響更能體現實際受力狀況。

4 結果分析

本節就變形和應力對第四組的結果進行分析。為了驗證其合理性,將其與未考慮卸荷效應的情況進行對比。

4.1 應力和塑性區

（1）開挖前

圖5為自重作用下邊坡的第一主應力分布圖。由圖可知,在左岸邊坡位置,拉應力區主要集中在第二級和第五級馬道附近以及坡頂處。其中,第二級馬道附近的拉應力約為0.1 MPa～0.5 MPa,第五級馬道附近及坡頂處的拉應力約為0.5 MPa～0.8 MPa。其它區域無明顯拉應力存在。從圖6 塑性區分布圖可知,僅在坡腳處有部分區域出現了壓剪破壞,其他區域沒有分析塑性區分布,這是由于自重作用產生的。

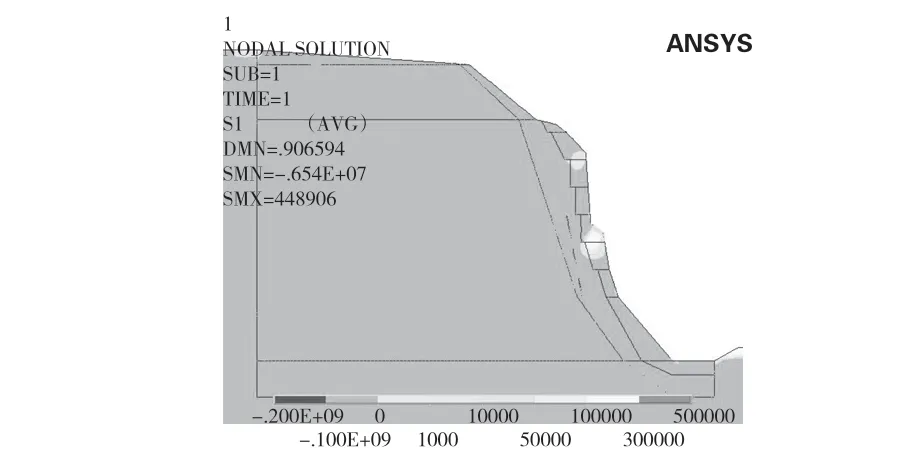
圖5 邊坡拉應力圖

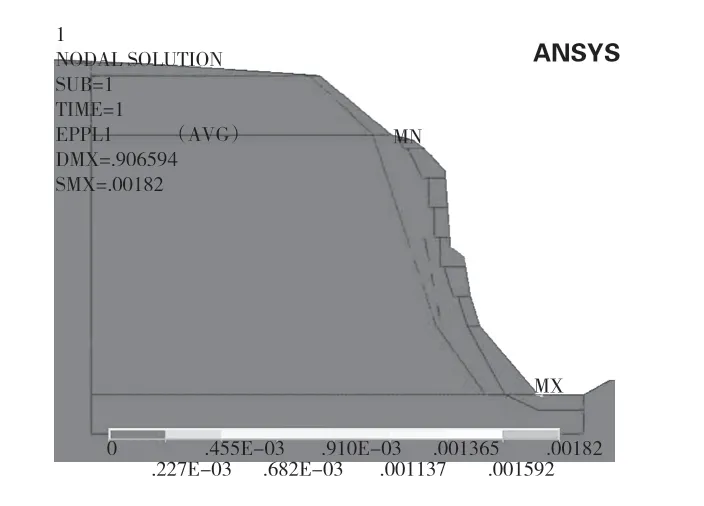
圖6 塑性區分布圖

（2）開挖后

由圖7、圖8可知,拉應力區在開挖形成的馬道下部出現,其拉應力值約為0.1 MPa～1 MPa。局部區域的拉應力值達到了6.2 MPa,即已經發生了破壞。從塑性區圖中不難發現這些區域已經形成了局部塑性區,但未連通。因此,有必要采取一定的技術手段來保證在施工過程中的邊坡穩定性。

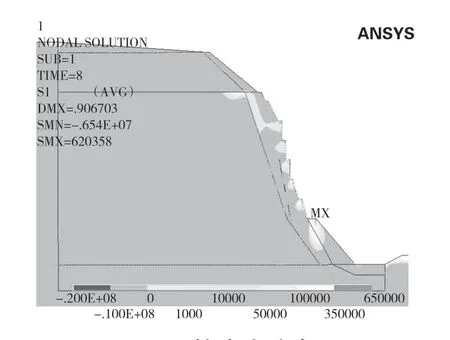
圖7 拉應力分布圖

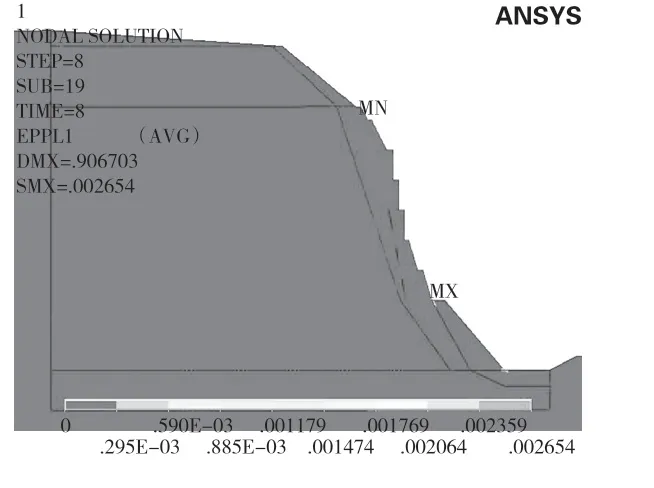
圖8 塑性區分布圖

4.2 邊坡位移分析

本節選取了10 個關鍵點以便于研究分析邊坡在開挖過程中產生的位移,其位置分布見圖9。

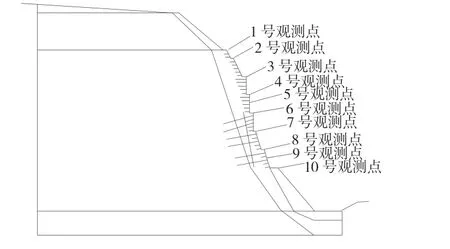
圖9 位移觀測點位置圖

圖10、圖11 和圖12 為3 個測點的位移時程曲線,這幾個關鍵點是具有一定代表性的。由時程曲線圖可以看出,邊坡開挖在Y方向引起的位移是相對穩定的。邊坡會發生整體向下的位移考慮到這是由于自重的作用。開挖卸載開始后,邊坡位移就開始發生了一定的回彈,這一現象通過Y方向的位移時程曲線圖得到了驗證。不同于Y方向的變化,X方向在進行逐步開挖時會在形成的新坡面產生反方向的位移,進一步開挖后,坡面的位移方向又回到了X方向。因此,X方向的整體位移變化規律是比較復雜。由于山體外形特征的影響會出現一些特殊位置,如10 號點是邊坡上的一個內凹關鍵點。該關鍵點由于自重作用會在X方向產生較大的位移并出現應力集中現象。這些位置的點均產生了 X方向的位移,這是由于部分區域發生擠壓作用促使的。因此,在開挖該點附近的巖體時會產生規律性的向反方向的位移,見圖10～圖12。開挖結束后,10 號點在X方向也就不再產生位移了。

圖10 X、Y方向的位移圖9(1號點)

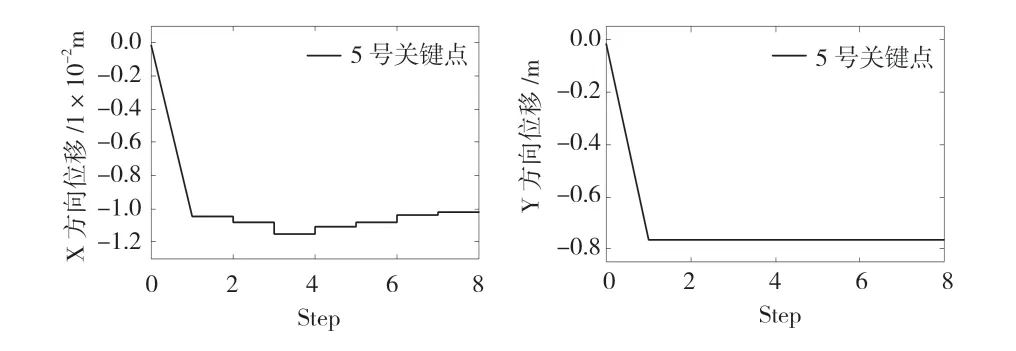
圖11 X、Y方向的位移圖( 5號點)

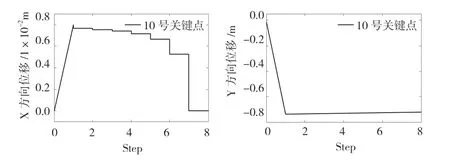
圖12 X、Y方向的位移圖(10號點)

4.3 考慮卸荷和未考慮卸荷的對比

（1）應力和塑性區分步

計算結果見圖13和圖14,圖7和圖8為第四組計算結果（見4.1.2節）。由對比可知,兩組應力結果在量值上無明顯差異。其中第三組最大拉應力為5.5 MPa,第四組最大應力為6.2 MPa,兩組相差13%。在塑性區方面,兩組均在坡腳處的部分區域出現塑性區。第三組未塑性區,而第四組會產生局部的塑性區,該區域是在開挖形成后的馬道下部產生的。第三組和第四組出現的最大塑性應變分別為0.0019、0.0026,兩者相差37%。

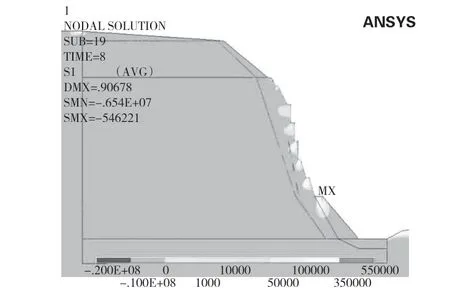
圖13 拉應力區分布

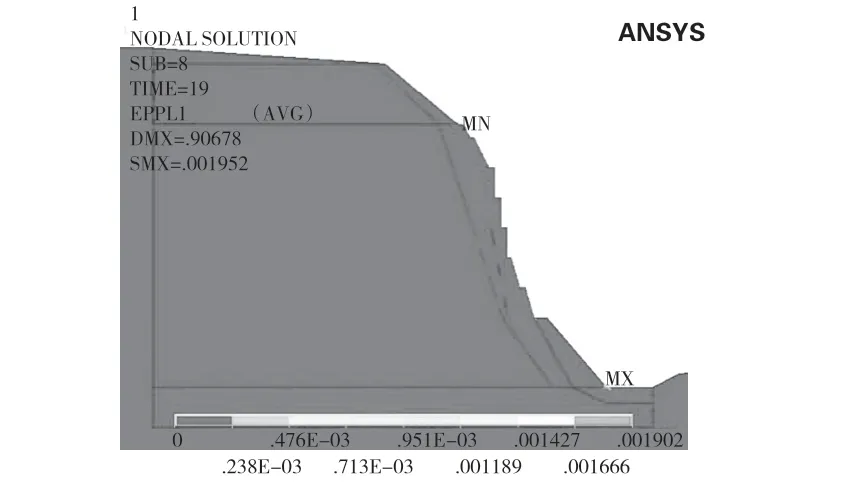
圖14 塑性區

（2）位移值對比分析

第三組和第四組的位移結果見表2。由表2可知：關鍵點1～8號的位移結果從坡底到坡頂呈現逐漸減小的趨勢。這是巖體應力大小不同和開挖體相對坡體較小造成的。通過對比三、四組的位移結果發現未考慮卸荷效應的位移結果值要小于考慮了卸荷效應的位移結果。參考工程監測數據發現考慮卸荷效應的結果值更接近實際測量位移值。

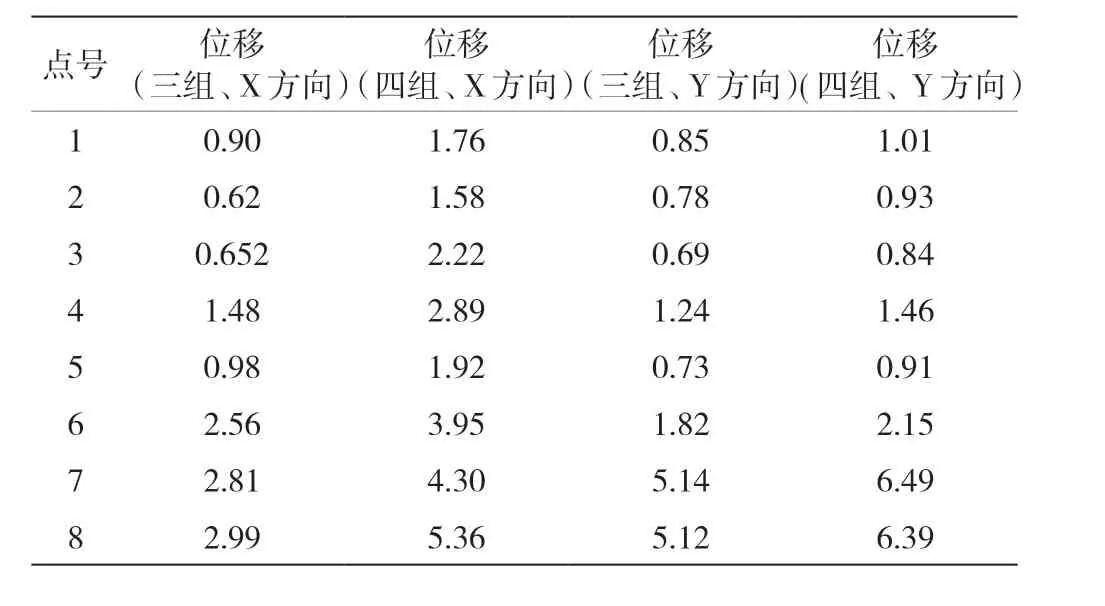
表2 關鍵點的位移表

5 結論

本文基于某水庫地質構造、施工工況、巖體物理力學參數,通過ANSYS對開挖坡面進行了數值分析。通過對比不對裂隙進行處理、灌漿的方法對裂隙進行處理、考慮錨索的加固效應、考慮巖體開挖過程的卸荷效應的四種不同工況,得到了下列結論：

（1）由于X1 裂隙開口較大,張開角度最大處為0.45 m,且距離開挖面較近,不進行處理的模型第五步出現不收斂,直接開展施工安全性較低,對裂隙進行灌漿處理更有利于邊坡開挖的穩定性。

（2）由于裂隙的擴展,灌漿后的裂隙也不能完全保持穩定,完成了前六步開挖模擬計算,但第七步的開挖模擬計算過程中出現不收斂。由于第六步完成后開挖巖方量較大,卸荷作用較為明顯第六步開挖后的馬道與第七步開挖的巖體出現了較大區域的塑性變形,因而需要采取錨索加固的方式對邊坡進行加固,以保證巖體邊坡的穩定性。

（3）通過對第三、四組模擬結果的對比分析比較,計算工況將錨索的加固效應加入模擬中,使得模型的模擬計算結果收斂。但考慮卸荷效應時計算的結果較不考慮時大,因而應用于工程實踐中是偏于安全的。

（4）從工程的實際施工過程也得以驗證,考慮巖體開挖過程中的卸荷效應與實際工程應用過程中更相符。