例析幾何體外接球運算中的等量關系

馬國良

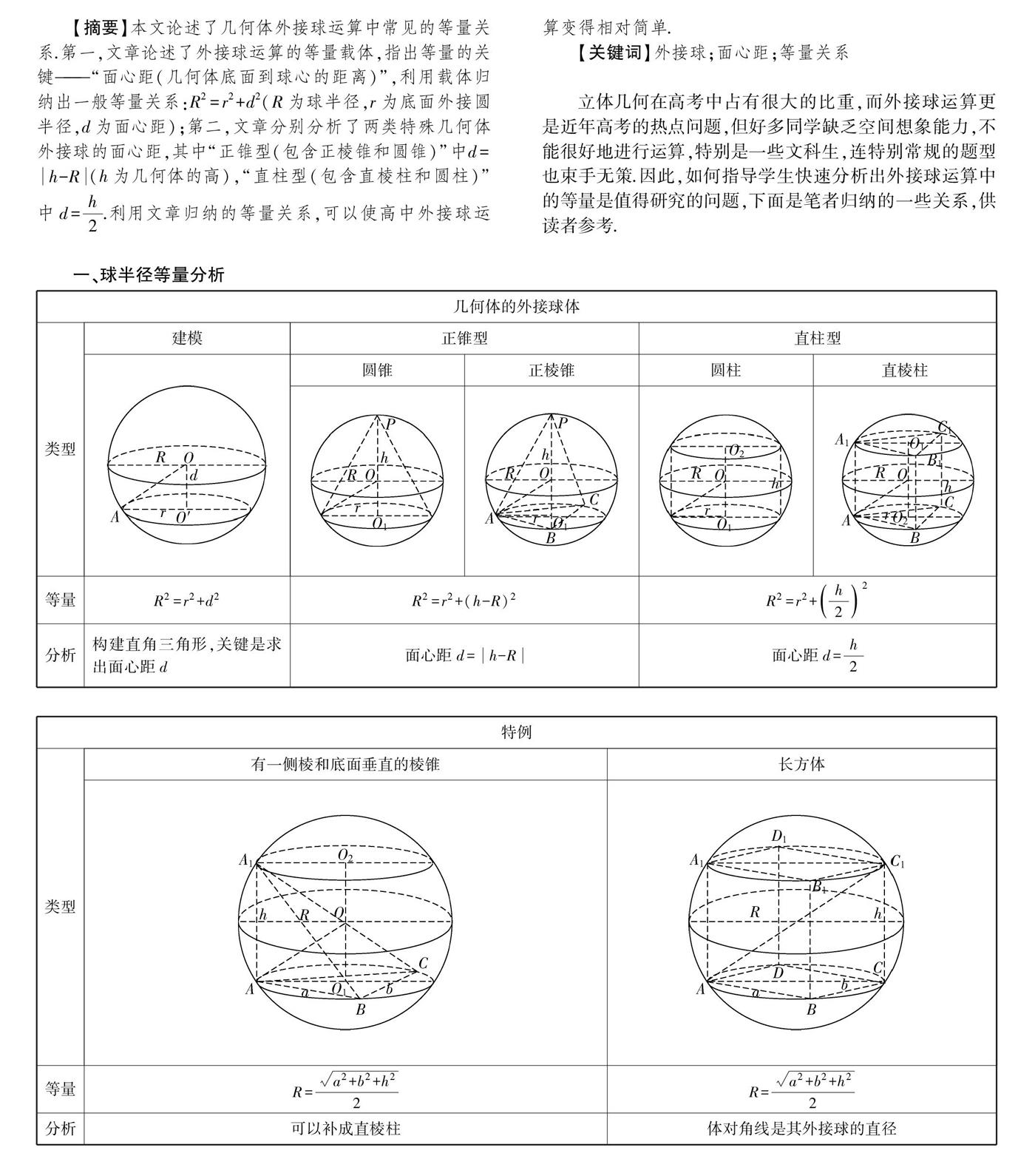
【摘要】本文論述了幾何體外接球運算中常見的等量關系.第一，文章論述了外接球運算的等量載體，指出等量的關鍵——“面心距（幾何體底面到球心的距離）”，利用載體歸納出一般等量關系：R2=r2+d2（R為球半徑，r為底面外接圓半徑，d為面心距）;第二，文章分別分析了兩類特殊幾何體外接球的面心距，其中“正錐型（包含正棱錐和圓錐）”中d=h-R（h為幾何體的高），“直柱型（包含直棱柱和圓柱）”中d=h2.利用文章歸納的等量關系，可以使高中外接球運算變得相對簡單.

【關鍵詞】外接球;面心距;等量關系

立體幾何在高考中占有很大的比重，而外接球運算更是近年高考的熱點問題，但好多同學缺乏空間想象能力，不能很好地進行運算，特別是一些文科生，連特別常規的題型也束手無策.因此，如何指導學生快速分析出外接球運算中的等量是值得研究的問題，下面是筆者歸納的一些關系，供讀者參考.

一、球半徑等量分析

三、案例分析

（一）等量載體

例1 （2012年全國Ⅱ卷）平面α截球O的球面所得圓的半徑為1，球心O到平面α的距離為2，則此球的體積為.

分析 本題直接告訴了面心距d和底面半徑r，可以直接用等量關系R2=r2+d2.

解 由R2=r2+d2，球半徑R=3，故V球=43πR3=43π（3）3=43π.

評析 球體中幾何法的關鍵是“面心距”，球半徑、底面半徑、面心距構成了一個直角三角形.

（二）正錐型

例2 若正四面體的邊長為3，則其外接球體的半徑是多少？

分析 正四面體是特殊的正棱錐，其外接球等量滿足R2=r2+（h-R）2，這樣不用畫圖就可以快速進行運算.

解 正四面體的底面半徑r=33a，h=a2-r2=63a，由R2=r2+（h-R）2，得球半徑R=64a.故R=364.

評析 很顯然，我們如果能夠把握“正錐型”幾何體的特征，搞清其外接球運算的等量關系，進行相關運算就非常容易了.

（三）直柱型

例3? 若正六棱柱底邊長為6，高為16，則其外接球體的半徑是多少？

分析 正六棱柱屬“直柱型”，滿足公式R2=r2+h22.

解 由正六邊形外接圓的半徑等于邊長，得底面半徑r=6，h=16，由R2=r2+h22，得球半徑R=10.

評析 我們如果能夠搞清楚幾何體的外接球運算的等量關系，不用畫圖，直接就可以進行運算了.

（四）一側棱與底面垂直的棱錐

例4 若三棱錐P-ABC的底面邊長AB=6，AC=8，AB⊥AC，側棱PA=24，PA與底面垂直，則其外接球體的半徑是多少？

分析 三棱錐P-ABC不是正棱錐，但通過“填補”可以得出其與以△ABC為底面，PA為側棱的直三棱柱共外接球體，可以通過“直柱型”等量關系予以計算.同時，如果繼續“填補”，發現其與分別以AB，AC，PA為長、寬、高的長方體共外接球體，長方體外接球體半徑是其體對角線，即R=a2+b2+h22（a，b，h分別為長方體的長、寬、高）.

解 方法一：幾何體的底面半徑r=BC2=102=5，h=PA=24，由R2=r2+h22，得球半徑R=13.

方法二：由長方體球半徑R=a2+b2+h22，得R=62+82+2422=13.

評析 本題中棱錐雖不是“正錐型”，但通過“填補”發現可以轉化為“直柱型”幾何體的外接球問題，并且是更特殊的長方體，學生只要能夠熟練掌握這些幾何體外接球運算的等量關系，就可以輕松解決問題.

（五）長方體

例5 （2017年全國Ⅱ卷）長方體的長、寬、高分別為3，2，1，其頂點都在球O的球面上，則球O的表面積為.

分析 長方體外接球體半徑是其體對角線，即R=a2+b2+h22（a，b，h分別為長方體的長、寬、高）.

解 由長方體球半徑R=a2+b2+h22，得R=32+22+122=142，則S球=4πR2=14π.

評析 本題中幾何體為長方體，只要明確等量，解答就非常容易了.

總之，立體幾何問題較抽象，學生需要有一定的空間思維能力.我們只要堅持數形結合的思路，注重空間中的等量關系，就可以使抽象的問題簡單化、公式化.