對角矩陣研究
閆偉文

【摘要】對角矩陣是一種特殊的簡單矩陣,具有重要的性質與潛在的應用價值.本文重點總結了對角矩陣的計算、性質及相似對角化,進而推廣到分塊對角矩陣.
【關鍵詞】對角矩陣;相似對角化;分塊對角矩陣
【基金項目】山西省教育科學十三五規劃2020年度互聯網+教育研究專項課題+服務人工智能專業發展的大學數學課程體系建設研究(HLW-20145)
對角矩陣作為一種特殊的矩陣,有其獨特的運算及性質,是解決線性代數問題的一個重要工具.本文主要從對角矩陣的定義、運算、性質、相似對角化四個方面來研究對角矩陣,進而推廣到分塊對角矩陣.
一、對角矩陣的定義
形如矩陣A=a11a22ann(主對角線元素aiii=1,2,…,n不全為零,其余元素全為零)的方陣,稱為對角矩陣.
二、對角矩陣的運算
1.線性運算.
(1)加法運算.
設對角矩陣A1=a11a22ann,A2=b11b22bnn,則矩陣A1±A2=a11±b11a22±b22ann±bnn,此為對角矩陣的和矩陣,即兩個對角矩陣的和為這兩個對角矩陣主對角線元素對應求和.
(2)數乘運算.
設對角矩陣A=a11a22ann,k為非零實數,則矩陣kA=ka11ka22kann,此為非零實數與對角矩陣的乘積,即數乘對角矩陣,數要乘到其主對角線的所有元素上.
2.乘法運算.
(1)兩個同階對角矩陣相乘.
設對角矩陣A1=a11a22ann,A2=b11b22bnn,則矩陣A1A2=a11b11a22b22annbnn,即兩個同階的對角矩陣相乘,為其主對角線元素對應相乘,可將其推廣到n個同階對角矩陣相乘.
(2)對角矩陣的冪.
設對角矩陣A=a11a22ann,m為非零自然數,則矩陣Am=a11ma22mannm為對角矩陣的m次冪,即主對角線上各元素的m次冪.
(3)對角矩陣乘同階矩陣.
設對角矩陣A=a11a22ann,矩陣A1=a11a12…a1na21a22…a2nan1an2…ann,則矩陣
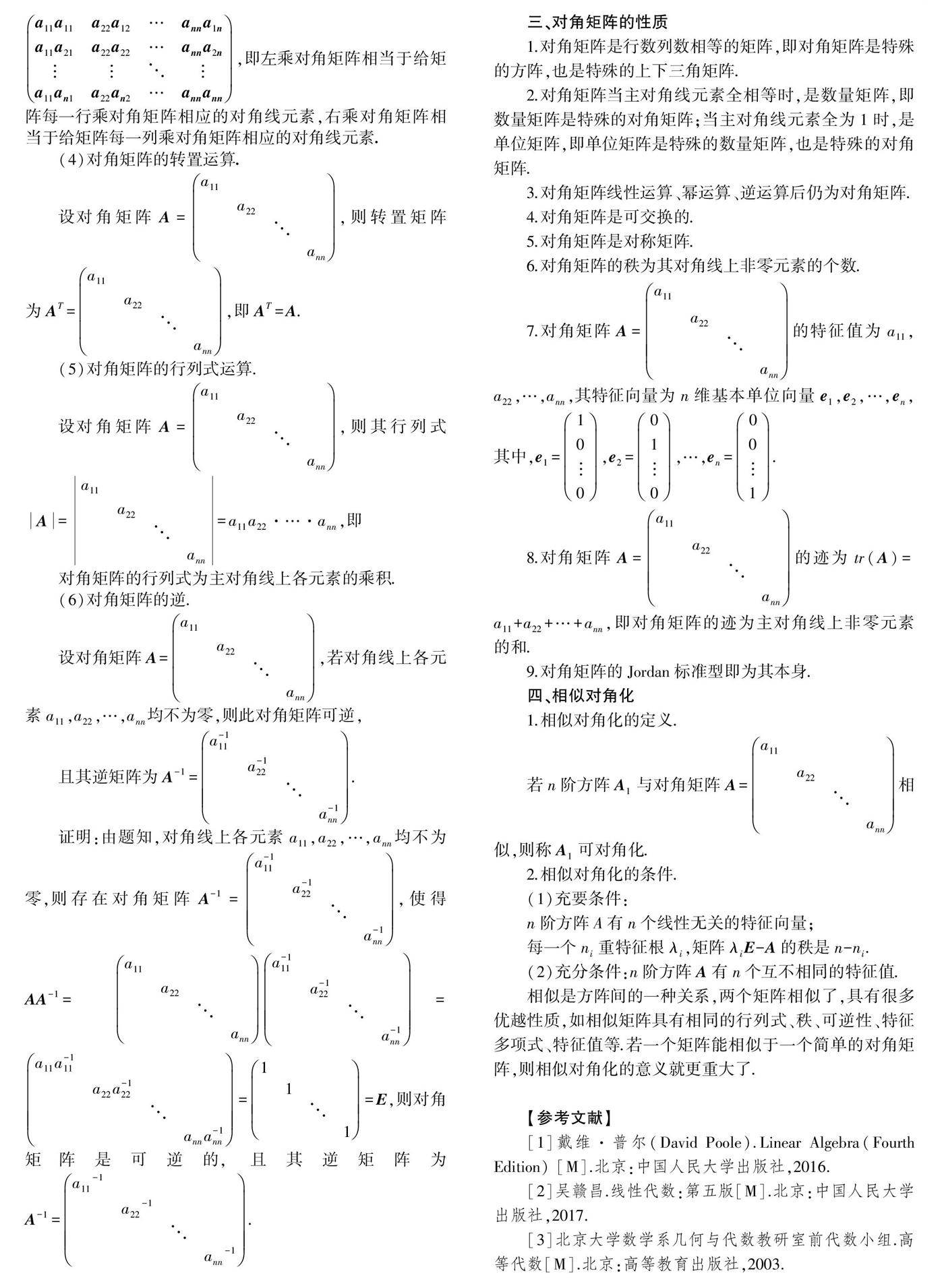
AA1=a11a11a11a12…a11a1na22a21a22a22…a22a2nannan1annan2…annann,A1A=a11a11a22a12…anna1na11a21a22a22…anna2na11an1a22an2…annann,即左乘對角矩陣相當于給矩陣每一行乘對角矩陣相應的對角線元素,右乘對角矩陣相當于給矩陣每一列乘對角矩陣相應的對角線元素.
(4)對角矩陣的轉置運算.
設對角矩陣A=a11a22ann,則轉置矩陣為AT=a11a22ann,即AT=A.
(5)對角矩陣的行列式運算.
設對角矩陣A=a11a22ann,則其行列式A=a11a22ann=a11a22·…·ann,即
對角矩陣的行列式為主對角線上各元素的乘積.
(6)對角矩陣的逆.
設對角矩陣A=a11a22ann,若對角線上各元素a11,a22,…,ann均不為零,則此對角矩陣可逆,
且其逆矩陣為A-1=a-111a-122a-1nn.
證明:由題知,對角線上各元素a11,a22,…,ann均不為零,則存在對角矩陣A-1=a-111a-122a-1nn,使得AA-1=a11a22anna-111a-122a-1nn=a11a-111a22a-122anna-1nn=111=E,則對角矩陣是可逆的,且其逆矩陣為A-1=a11-1a22-1ann-1.
三、對角矩陣的性質
1.對角矩陣是行數列數相等的矩陣,即對角矩陣是特殊的方陣,也是特殊的上下三角矩陣.
2.對角矩陣當主對角線元素全相等時,是數量矩陣,即數量矩陣是特殊的對角矩陣;當主對角線元素全為1時,是單位矩陣,即單位矩陣是特殊的數量矩陣,也是特殊的對角矩陣.
3.對角矩陣線性運算、冪運算、逆運算后仍為對角矩陣.
4.對角矩陣是可交換的.
5.對角矩陣是對稱矩陣.
6.對角矩陣的秩為其對角線上非零元素的個數.
7.對角矩陣A=a11a22ann的特征值為a11,a22,…,ann,其特征向量為n維基本單位向量e1,e2,…,en,其中,e1=100,e2=010,…,en=001.
8.對角矩陣A=a11a22ann的跡為tr(A)=a11+a22+…+ann,即對角矩陣的跡為主對角線上非零元素的和.
9.對角矩陣的Jordan標準型即為其本身.
四、相似對角化
1.相似對角化的定義.
若n階方陣A1與對角矩陣A=a11a22ann相似,則稱A1可對角化.
2.相似對角化的條件.
(1)充要條件:
n階方陣A有n個線性無關的特征向量;
每一個ni重特征根λi,矩陣λiE-A的秩是n-ni.
(2)充分條件:n階方陣A有n個互不相同的特征值.
相似是方陣間的一種關系,兩個矩陣相似了,具有很多優越性質,如相似矩陣具有相同的行列式、秩、可逆性、特征多項式、特征值等.若一個矩陣能相似于一個簡單的對角矩陣,則相似對角化的意義就更重大了.
【參考文獻】
[1]戴維·普爾(David Poole).Linear Algebra(Fourth Edition) [M].北京:中國人民大學出版社,2016.
[2]吳贛昌.線性代數:第五版[M].北京:中國人民大學出版社,2017.
[3]北京大學數學系幾何與代數教研室前代數小組.高等代數[M].北京:高等教育出版社,2003.

