某型號配砟車動力學性能分析
張 超,李 帥,余 砥,張勁松,周明剛
(湖北工業大學農機工程研究設計院,湖北 武漢 430068)
配砟車是專門為道床的配砟整形開發的一種大型養路機械,其主要功能是在搗固和穩定作業施工后,通過對道床上的道砟進行分配、搬移、整形和清掃,以實現道床的配砟整形[1-2]。軌道工程車輛運行安全性是其設計研發的核心問題,動力學特性分析是研究軌道車輛運行安全性的常用技術手段。Lee,Jin-Ho等[3]建立了混合動力列車模型,并采用SC-LSM技術,研究了模型磁剛度對列車運行穩定性的影響。羅仁等[4]用數值計算方法分析了列車運行的平穩性,認為橫向連接阻尼和剛度對列車橫向平穩性影響顯著。劉宏友等[5-6]利用列車動力學分析軟件TVDYNA1.0、常微分方程一次近似理論及Hopf分叉理論,重點研究了列車的非線性運行穩定性。周勁松等[7]采用面向對象的建模技術建立了帶車輛間懸掛系統的三輛車編組以及單車的垂向及橫向非線性動力學模型,研究表明加入懸掛系統增加列車高速運行時的平穩性。曾元辰等[8]利用改進的AGREE可靠度分配算法研究列車運行的穩定性。
本文以某型號配砟車為研究對象,基于多體動力學法,采用牛頓-歐拉方程構建其數值模型,依據GB/T 17426-1998[9],以運行平穩性、運行穩定性和曲線通過性為衡量指標,對該配砟車的動力學性能進行分析,對其運行安全性進行校核計算。
1 配砟車動力學仿真模型
多體動力學法是研究列車動力學性能的常用方法,對于列車模型的構建常采用牛頓-歐拉動力學法。牛頓-歐拉動力學法將列車看成由多個剛體部分通過彈簧阻尼單元連接組成的多體系統(圖1)。圖1中,MC、Mb分別為車體質量之半和構架質量之半;K1、K2分別為一系和旁承的一側的垂向剛度;C1、C2分別為一系和旁承一側的垂向阻尼;V為車輛運行速度;XC、Xb1、Xb2分別為車體、前構架和后構架的垂向位移;βc、βb1、βb2分別是車體、前構架和后構架的點頭角位移;Xr1~Xr4為軌道不平順位移輸入。
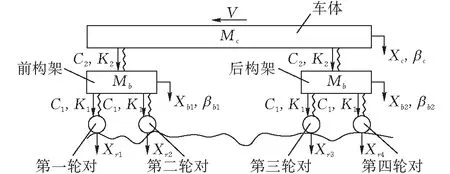
圖 1 配砟車二維拓撲結構
根據圖1的配砟車二維拓撲模型,由牛頓第二定理構建配砟車的運動方程[10]:
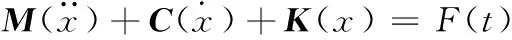
(1)
采用四階龍格-庫塔數值積分法對整個運動方程矩陣進行求解,即可得到配砟車的振動響應。
依據上述多體動力學理論,采用多體動力學軟件Simpack,建立某型號配砟車仿真計算模型(圖2)。該型號配砟車相關參數如表1所示。模型主要有車體1個、轉向架構架2個、輪對4個和軸箱8個。車體、輪對和轉向架構架各有6個自由度,軸箱的自由度為1,整個機車系統共計50個自由度。其中一系懸掛采用的是無間隙的彈性懸掛系統,可使配砟車具有良好通過性能及行車穩定性能。在該型號配砟車模型中,車體、輪對和轉向架的連接方式為鐵路鉸接,車輪踏面類型為LM型,鋼軌類型為50軌類型。
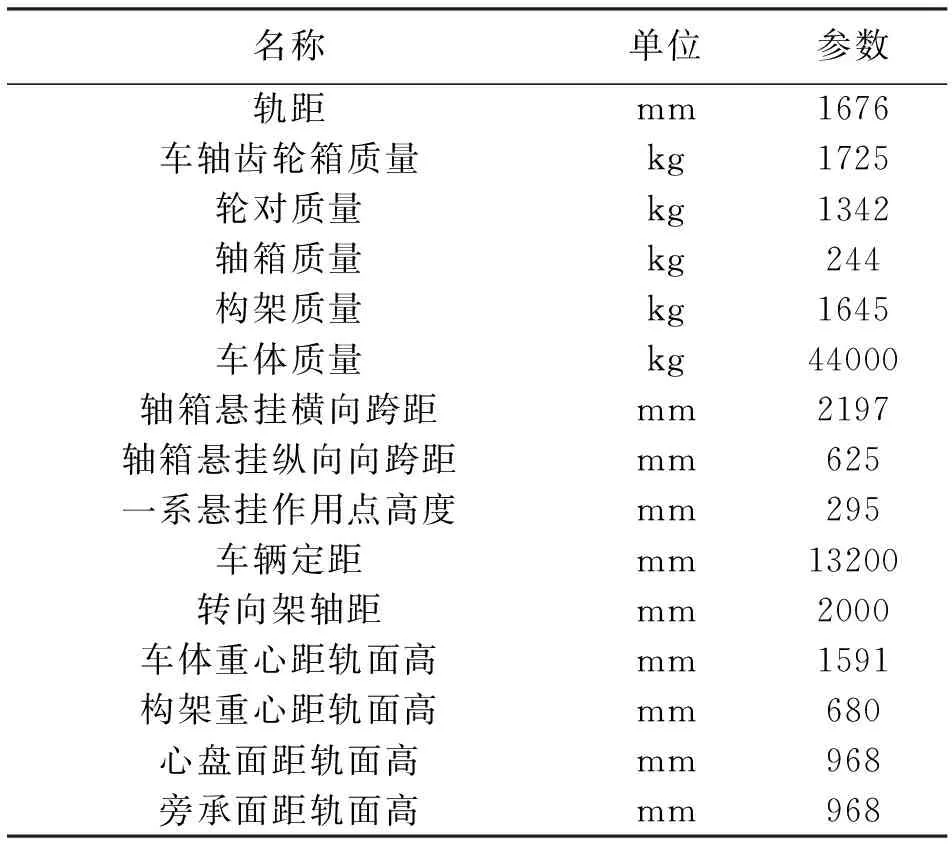
表1 配砟車結構參數

圖 2 配砟車多體動力學模型
2 配砟車動力學性能
車輛的動力學性能主要包括運行穩定性、運行平穩性和曲線通過性等三項內容[11]。本文以上述三項性能指標,結合國家標準GB/T 17426-1998內容,對該型號配砟車的動力學性能進行分析計算。
2.1 配砟車運行穩定性
運行穩定性是防止車輛蛇行運動的重要衡量指標,其研究方法是使用四階龍格-庫塔數值積分法對配砟車多體動力學運動方程在外界激勵條件下進行求解,分析車輛在不同運行速度下第一輪對和第三輪對的橫向位移隨時間的變化情況。如果其橫向位移收斂則車輛運行時是穩定的,發散則處于失穩狀態;當橫向位移既不發散也不收斂,則此時對應的速度為車輛的非線性臨界速度。如果車輛的非線性臨界速度高于最高設計運行速度,則說明車輛運行穩定性滿足運行要求[11]。
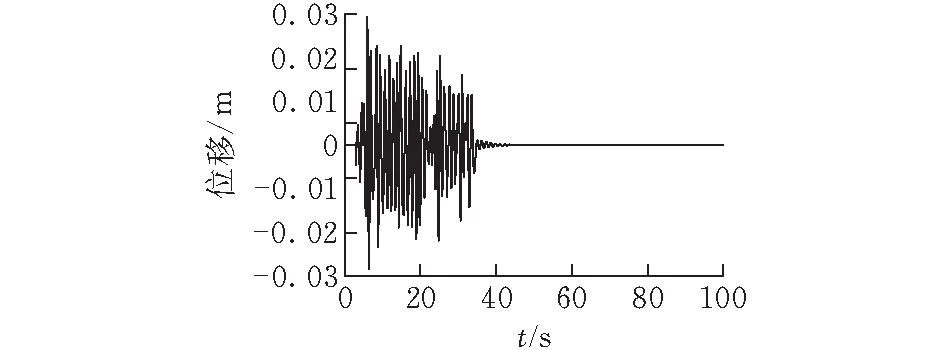
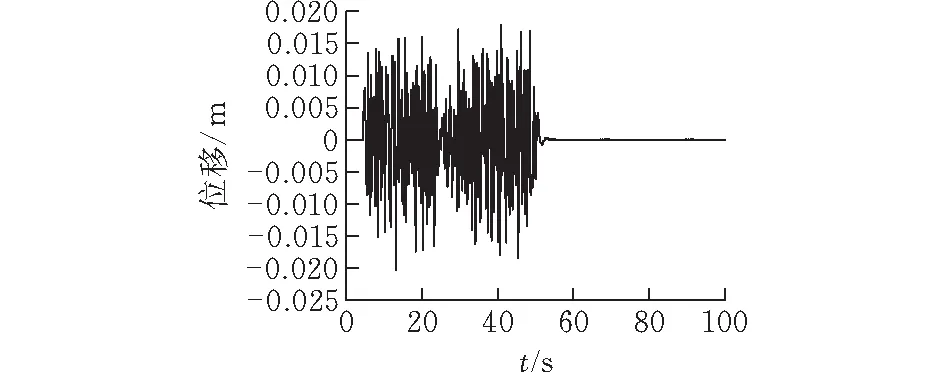
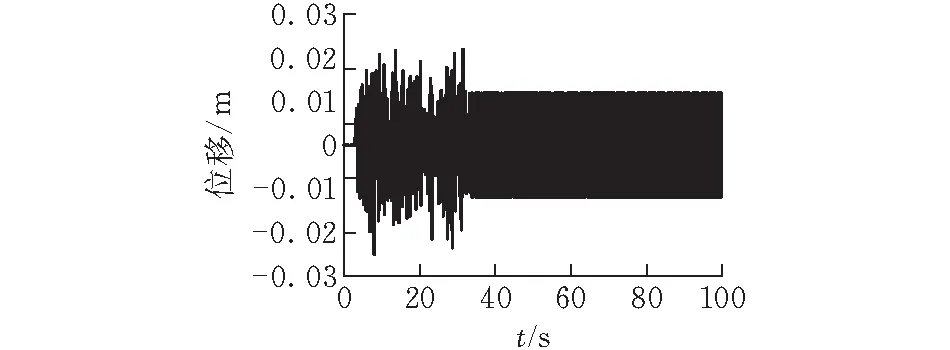
配砟車運行過程中的激勵是由軌道線路不平順引起的。美國聯邦管理局FRA根據大量實測資料得到線路不平順功率譜密度,并將其擬合成了一個以階段頻率和粗糙度常數表示的偶次函數,據此將軌道分為6個等級,即:Ⅰ級最差,Ⅵ級最好[10]。美國Ⅴ級線路軌道譜波長范圍為1.524~304.8 m,與本文配砟車運行線路質量相當,因此計算過程中,以美國Ⅴ級線路軌道譜作為激勵輸入。配砟車運行線路總長度為10 000 m,激勵施加到20~1000 m的線路上,分別對運行速度為100 、116 和117 km/h時配砟車第一輪對和第三輪對的橫向位移隨時間的變化進行了計算,結果分別如圖3—5所示。
(a)第一輪對
(a)第一輪對
(a)第一輪對
從圖5可以看出,配砟車行駛速度為117 km/h時,第一和第三輪對的橫向位移出現穩定的周期振動,既不收斂也不發散,即車輛處于非收斂臨界狀態。圖3和圖4中配砟車行駛速度分別為100 km/h和116 km/h,可見當速度小于117 km/h時,第一和第三輪對的橫向位移處于收斂狀態。因此表明該型號配砟車的蛇行運動失穩臨界速度Vcr為117 km/h,大于該型號配砟車最高設計速度100 km/h,且具有一定的速度裕量,說明該型號配砟車運行穩定性滿足運行要求。
2.2 配砟車運行平穩性
運行平穩性主要反映了車輛本身的運行品質,同樣采用四階龍格-庫塔數值積分法對配砟車動力學模型在美國Ⅴ級線路軌道譜激勵條件下的動態響應進行求解,采用Sperling平穩性指標法可求出車輛的平穩性指標[11]。
W=(a3b3)1/10
(2)
(3)
式中:a是加速度幅值,b是加速度的計權系數,f為振動頻率。
根據國家標準[9],如果平穩性指標W小于3.0,則車輛的運行平穩性等級為優;若W在3.0~3.5之間,則其等級為良;當W處于3.5~4.0之間,則其等級為合格;而當W大于4.0,則不合格。分別提取配砟車運行過程中的最大橫向加速度Ay和垂向加速度Az,當Ay小于4.905 m/s2,Az小于6.867 m/s2時,則車輛的運行平穩性符合運行要求。
依據式(2)分別對車輛運行速度為50~110 km/h配砟車的橫向平穩性指標Wy及垂向平穩性指標Wz進行計算,并提取車輛的橫向及垂向最大加速度Ay和Az,結果如表2所示。
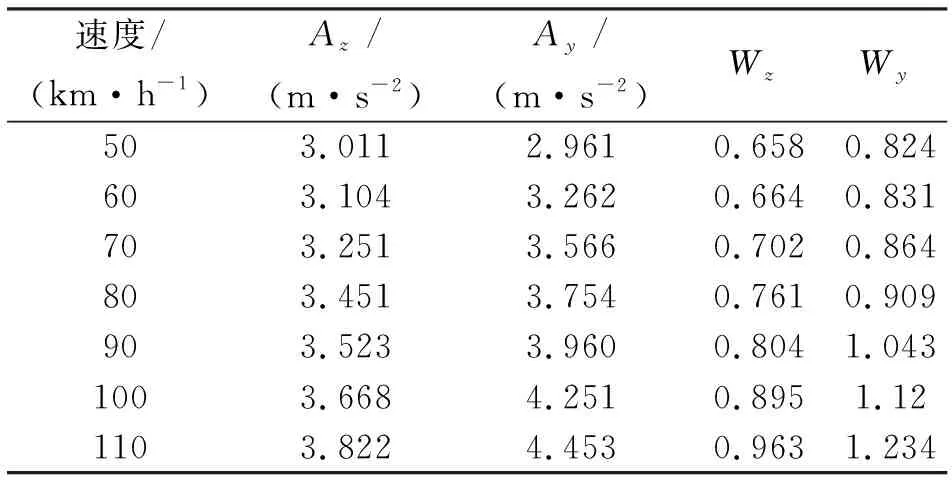
表2 配砟車運行平穩性計算結果
從表2可以看出,車輛運行速度為50~110 km/h速度范圍內,配砟車的橫向和垂向平穩性指標均小于3.0,屬于GB/T1 7426-1998規定的優級標準,而且所有的最大橫向加速度均小于4.905 m/s2,最大垂向加速度均小于6.867 m/s2。因此說明該型號配砟車運行平穩性滿足運行要求。
2.3 配砟車曲線通過性分析
曲線通過性是關乎車輛運行安全性的重要衡量指標。車輛由直線駛入曲線時,特別是通過緩和曲線時,其受力特征將會出現明顯變化。這一過程可以通過采用數值積分法對車輛通過有限長的曲線(特別是緩和曲線)時的響應進行求解分析,在此基礎上計算出脫軌系數,并提取輪軸橫向力,據此衡量車輛的曲線通過性[11]。
依據國家標準可知[9],輪軸橫向力容許限度Hmax為76.87 kN,且規定第一限度即危險限度脫軌系數為Q/P≤1.2,第二限度即允許限度脫軌系數為Q/P≤1.0,其中Q為爬軌側車輪作用于鋼軌上的橫向力,P為爬軌側車輪作用于鋼軌上的垂向力。當車輛通過規定曲線時,其輪軸橫向力H小于Hmax,且其脫軌系數Q/P最大值不大于1.2時,則可證明該型號配砟車的曲線通過性滿足要求。
根據該型號配砟車實際運行情況,分析車輛曲線通過性時線路條件如下:
1)曲線半徑R=300 m,曲線外軌超高h=95 mm,運行速度V=40 km/h;
2)曲線半徑R=400 m,曲線外軌超高h=85 mm,運行速度V=45 km/h;
3)曲線半徑R=500 m,曲線外軌超高h=80 mm,運行速度V=55 km/h;
4)曲線半徑R=600 m,曲線外軌超高h=75 mm,運行速度V=60 km/h。計算結果如表3所示。從表3可見,配砟車在通過不同半徑曲線時,其輪軸橫向力H均小于輪軸橫向力容許限度Hmax、脫軌系數Q/P均小于第一限度脫軌系數1.2,其曲線通過性滿足要求。
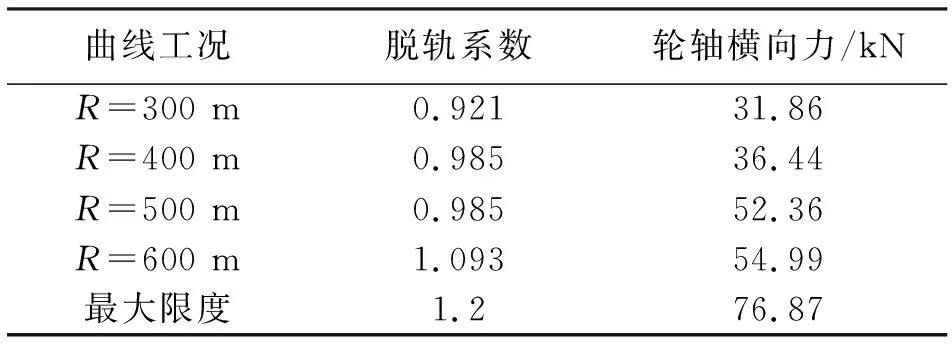
表3 配砟車曲線通過性
3 結束語
本文采用牛頓-歐拉方程,基于Simpack動力學軟件建立了某型號配砟車的多體動力學模型。以此為基礎,對該型號配砟車的運行穩定性、運行平穩性和曲線通過性進行了分析,所得具體結論如下:
1)該配砟車在美國Ⅴ級線路上行駛,其蛇行失穩臨界速度為117 km/h,高于所設計的100 km/h的最高運行速度。
2)該配砟車在110 km/h速度內的橫向和垂向平穩性指標小于3.0,滿足有關國家標準規定的優級標準;在110 km/h速度范圍內,配砟車的最大橫向加速度小于4.905 m/s2,最大垂向加速度小于6.867 m/s2,均滿足有關國家標準規定的要求。
3)該配砟車以40 km/h的速度通過半徑為300 m的圓曲線、以45 km/h的速度通過半徑為400 m的圓曲線、以55 km/h的速度通過半徑為500 m的圓曲線以及以60 km/h的速度通過半徑為600 m的圓曲線時,輪軸橫向力H、脫軌系數Q/P均小于國家標準規定的最大限度值。
從上述研究結果可知,該型號配砟車各參數指標均符合國家標準GB/T 17426-1998規定,滿足設計要求。

