動力冗余液體捆綁火箭的POGO穩定性分析

王 濤，容 易，胡久輝，唐 冶，丁 千

(1. 天津大學機械工程學院，天津 300072；2. 北京宇航系統工程研究所，北京 100076)

0 引 言

通過推進系統與箭體結構系統的相互耦合，使液體火箭產生的縱向低頻自激振動稱為POGO振動[1-3]。POGO振動可能發生在飛行過程中的任意時刻，對運載器的安全性和液體火箭發射可靠性造成嚴重威脅，對于載人火箭甚至危及宇航員的生命安全，國內外均展開了大量研究。Rubin[4]提出了液體火箭POGO振動的頻域分析法，并成功應用此方法分析了大力神Ⅱ運載火箭POGO振動問題。徐得元等[5]利用有理多項式對POGO振動系統中擾動力的傳遞函數逼近，簡化了文獻[4]所建立的頻域模型。劉濤等[6]基于頻域分析法建立火箭POGO振動系統的傳遞函數。采用矢量擬合法對傳遞函數進行有理分式擬合，借助極點分布圖確定了蓄壓器能量值對POGO穩定性的影響。文獻[7]應用頻域法分析捆綁火箭的POGO穩定性，將推進系統簡化為多個獨立的單推進劑-單發動機系統。以上是利用頻域分析方法，研究液體火箭POGO穩定性問題。而時域方法也受到了眾多學者們的關注，Oppenheim和Rubin[8]從時域的角度提出了適用于任何液體火箭POGO振動系統的建模方法，給出了貯箱、推進劑管路系統、泵、蓄壓器和推力室等推進單元的建模過程，通過組裝單元動力學方程，建立液體火箭推進系統的擾動方程組和結構的縱向振動方程組。Zhao等[9]利用Rubin建模方法和Hurwitz穩定性判據導出單推進劑-單發動機火箭模型的POGO穩定條件，發現推進和結構系統的耦合強度直接影響液體火箭POGO穩定性。譚述君等[10-11]討論了臨界耦合強度理論和臨界阻尼比法在POGO穩定性分析中適應性問題，分析結果表明耦合強度是液體火箭是否發生POGO振動的決定因素。唐冶等[12]基于Rubin法和區間數學理論分析了推進系統頻率特性的靈敏度問題。Tang等[13]考慮氧化劑和燃料推進系統耦合的影響，利用Rubin法建立了液體火箭POGO振動系統的等效線性化動力學模型。采用Routh-Hurwitz判據，分析了推進系統參數對液體火箭POGO穩定性的影響。張青松和張兵[14]利用鍵合圖理論的思想，解決了Rubin模型的奇異性問題，提出新的液體火箭POGO穩定性分析的狀態空間模型，通過仿真證明了該模型的有效性和實用性。Wang等[15]基于獨立重量位移描述方法，將Rubin模型中的八種物理單元重新組合，提出了九種獨立單元，根據相同節點的脈動壓強相等為連接條件，建立微分方程形式的改進Rubin模型，該模型具有維數低和非奇異的優點。王慶偉等[16]利用改進的Rubin建模方法和混合坐標法建立了火箭姿態運動和POGO振動相互耦合的動力學模型，并進一步分析了泵增益和蓄壓器能量值對耦合系統穩定性的影響。文獻[17]基于改進Rubin方法和模態分解法對推進系統中的輸送管路動力學模型降維處理，提出了POGO振動系統時域模型的降維方法。

動力冗余技術[18]指運載火箭在一臺或數臺發動機出現故障的情況下，自動檢測、判別后發出指令關閉此發動機，實時切換或在線重構各分系統控制策略，能提高火箭飛行過程中的推進系統可靠性。大部分情況下，應用動力冗余技術可避免因發動機故障引起發射任務的失敗。但對于液體捆綁火箭而言，發動機故障[19-21]不僅會造成推力下降還會引起芯級和助推貯箱內推進劑消耗不均、火箭質心偏移、浪費運載能力等后果，這些問題的解決依賴于交叉輸送技術的應用。法爾肯9重型的早期方案采用該項技術保證助推和芯級推進劑按比例平穩消耗。航天飛機V-2通過應用交叉輸送技術確保助推器分離時軌道器貯箱仍處于滿箱狀態，有效提高了運載能力[22]。但在國內，具有交叉輸送能力的動力冗余火箭尚處于設計階段，僅有關于交叉輸送管路總體參數和方案設計的研究成果[23-24]。

本文針對推進劑的交叉輸送為動力冗余液體捆綁火箭POGO穩定性分析提出了新的任務，以獨立工作、一臺助推發動機故障助推貯箱向芯級發動機供給推進劑和兩助推器同時向芯級發動機供給推進劑三種工作模式為研究對象，利用改進Rubin建模方法[15]建立了液體捆綁火箭POGO振動系統的分析模型，分析了助推器和芯級的蓄壓器能量值、泵柔度和泵增益參數對不同工作模式下液體捆綁火箭POGO穩定性的影響。

1 液體捆綁火箭的POGO振動系統

具有交叉輸送功能的動力冗余液體捆綁火箭，可通過控制管路閥門的開閉，使推進系統根據實際情況在三種不同工作模式之間相互切換：獨立工作(Mode 1)，一臺助推發動機故障助推貯箱向芯級發動機供給推進劑(Mode 2)、兩助推器同時向芯級發動機供給推進劑(Mode 3)。其中Mode 1模式下推進系統交叉輸送管路處于關閉狀態，每臺發動機由獨立的氧路和燃路系統供給推進劑。Mode 2模式下發生故障的助推火箭與芯級火箭推進系統通過交叉輸送管路相互連通，存在耦合效應。Mode 3模式下芯級貯箱內的燃料和氧化劑不再消耗，各臺發動機所需的推進劑由助推貯箱供給。圖1為三種工作模式下動力冗余液體捆綁火箭的力學簡圖。

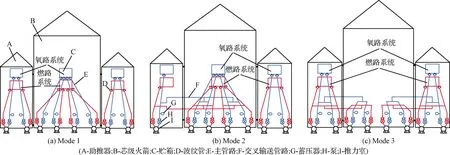
圖1 三種工作模式下動力冗余液體捆綁火箭Fig.1 The liquid strap-on launch vehicle with redundant propulsion system under three different working modes

基于改進Rubin建模方法，本文建立三種工作模式下(Mode 1, Mode 2, Mode 3)具有冗余能力的液體捆綁火箭POGO穩定性分析模型。改進的Rubin建模方法分為三步：1)通過有限元技術建立推進系統的動力學方程組；2)建立箭體結構縱向振動系統的模態方程；3)聯立推進系統和箭體結構系統的動力學模型，建立耦合系統的POGO穩定性分析模型。

1.1 推進系統動力學模型

根據改進Rubin建模方法中獨立單元的定義，對三種工作模式下動力冗余液體捆綁火箭推進系統進行了單元劃分，并依據以下兩個劃分原則((1)縱向管路劃分精細，橫向管路劃分粗糙；(2)忽略不可壓縮管、三通和彎頭的長度)得到十二種獨立單元：可壓縮管、單出口貯箱、推力室、波紋管-可壓縮管、可壓縮管-波紋管、三通-可壓縮管(單入口雙出口)、三通-蓄壓器、泵-不可壓縮管、雙出口貯箱、四出口貯箱、三通-可壓縮管(雙入口單出口)和彎頭-可壓縮管。其中八種獨立單元(可壓縮管、單出口貯箱、推力室、波紋管-可壓縮管、可壓縮管-波紋管、三通-可壓縮管(單入口雙出口)、三通-蓄壓器和泵-不可壓縮管)的動力學模型已由Wang等[15]給出，其余四種獨立單元的建模過程如下。

1)雙出口貯箱

雙出口貯箱共有兩個節點(見圖2(a))，t1和t2，這兩個節點均為推進劑流出節點。

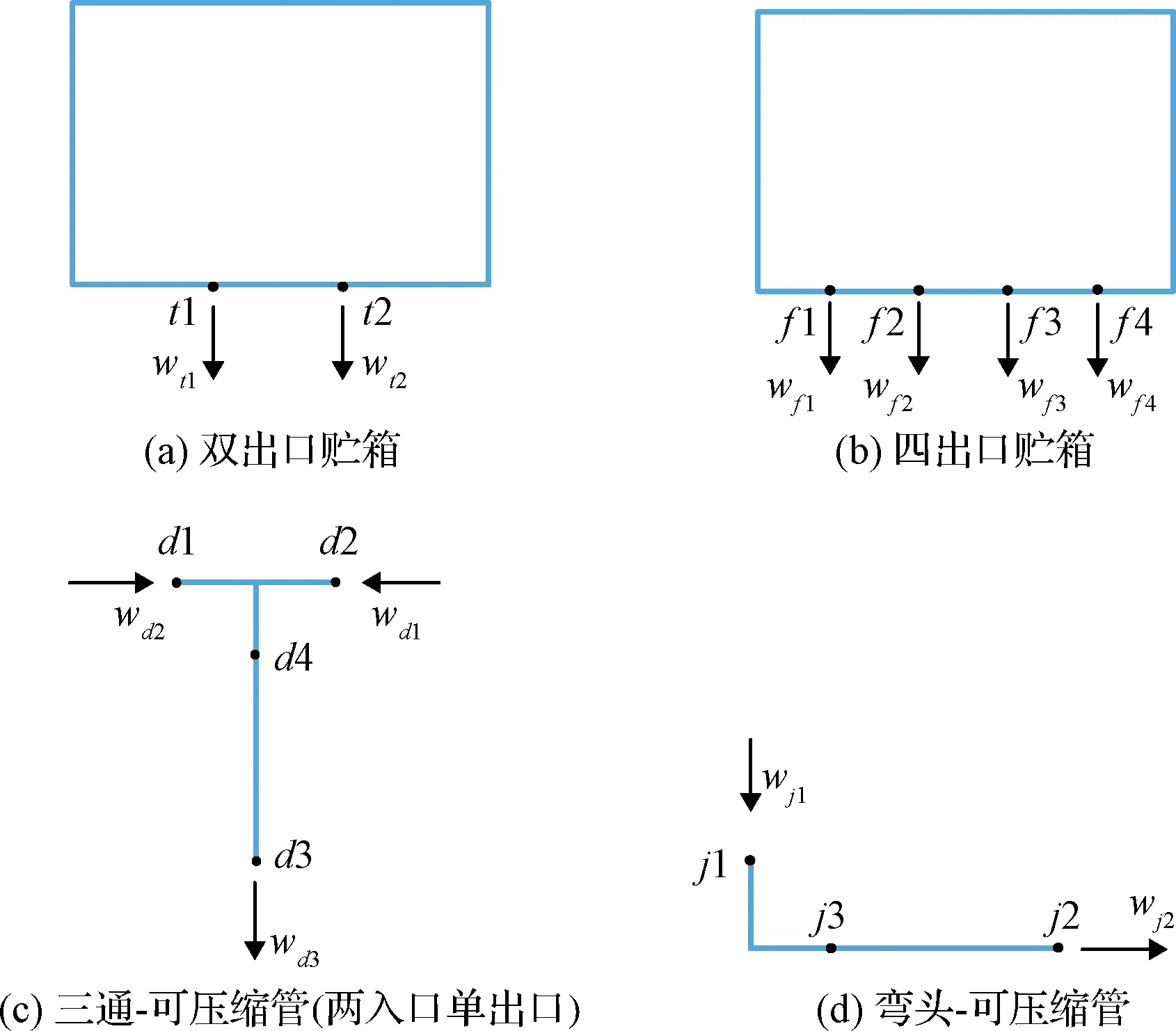
圖2 幾種推進系統獨立單元Fig.2 The schematic diagrams of partial independent unit

(1)動力學方程

假設貯箱內的液體凍結在單元中，應用牛頓定律建立其動力學方程為

(1)

式中：pt1,pt2分別為節點t1和t2的脈動壓強;Itt,Rtt為雙出口貯箱的慣性和阻尼;wtta和wtt表示雙出口貯箱內推進劑的絕對脈動重量位移和相對脈動重量位移，它們之間具有如下關系[8]

wtta=wtt+ρgAttNtt·rtte

(2)

式中：ρ,g為推進劑的密度和標準重力加速度;Att和Ntt分別表示雙出口貯箱出口的面積和方向向量;rtte為雙出口貯箱的位移矢徑。由于貯箱含有兩個出口，式(2)中的部分變量也可表示為

(3)

式中：wt1,At1,Nt1,wt2,At2和Nt2分別為t1和t2節點的相對脈動重量位移，截面積和方向向量。將式(2)和式(3)代入式(1)可得

(4)

式中：Htt為雙出口貯箱的水頭矢量，可表示為

Htt=(Nt1+Nt2)Ltt

(5)

式中：Ltt表示貯箱內液體的高度。

(2)雙出口貯箱對結構的作用力

多出口貯箱對結構的作用力等于每個出口作用力的疊加。單出口貯箱對結構的作用力可表示為[8]

(6)

雙出口貯箱對結構的作用力為

(7)

將式(4)代入式(7)可得

(8)

2)四出口貯箱

四出口貯箱的四個節點(見圖2(b)，f1,f2,f3和f4)均為推進劑流出節點。利用與雙出口貯箱相同的建模方法，可以得到四出口貯箱的動力學方程。

(1)動力學方程

(9)

式中：pf 1,wf 1,pf 2,wf 2,pf 3,wf 3,pf 4和wf 4分別為節點f1,f2,f3和f4的脈動壓強和重量位移;Ift,Rft,Hft和rfte為四出口貯箱的慣性、阻尼、水頭矢量和位移矢徑。

(2)四出口貯箱對結構的作用力

(10)

式中：Af 1,Nf 1,Af 2,Nf 2,Af 3,Nf 3,Af 4和Nf 4分別表示節點f1,f2,f3和f4的截面積和方向向量。

3)三通-可壓縮管(雙入口單出口)

雙入口單出口共有三個節點和一個連接點(見圖2(c))，d1,d2,d3和d4，其中d1和d2為推進劑流入節點，d3為流出節點，而d4為組合單元的連接點。

雙入口單出口的三通-可壓縮管與單入口雙出口的三通-可壓縮管具有完全相同的結構，僅d2節點的推進劑流動方向發生變化。因此只需令

(11)

單入口雙出口的三通-可壓縮管動力學方程[15]就可變為雙入口單出口的三通-可壓縮管動力學方程。

眾所周知，經費是開展一切工作的前提和基礎，然而經過調查，我國當前基層農機推廣中存在嚴重缺乏經費的現象，從根本上限制基層農機推廣服務體系，直接對推廣工作的效果產生不良影響。由于經費不足難以對農機技術進行全面演示及推廣，導致農民無法認識到其作用，極大地降低農民的購置積極性。除此之外，經費的匱乏還對員工的培訓和農機試驗等工作產生一定的阻礙，在一定程度上嚴重制約了基層農機推廣服務工作的發展。

(1)動力學方程

(12)

(13)

式中：pd1,wd1,pd2,wd2,pd3,wd3分別為節點d1,d2和d3的脈動壓強和重量位移，Itdc,Rtdc,Ktdc和rtde為可壓縮管部分的慣性、阻尼、剛度和矢徑;Htdc1,Htdc3則表示可壓縮管部分入口端到中點處和中點處到出口端的水頭矢量。

(2)三通-可壓縮管對結構的作用力

KtdcAtdc1(Ntdc1-Ntdc3)(wd1+wd2-wd3)+

(14)

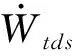
4)彎頭-可壓縮管

彎頭-可壓縮管共有兩個節點j1和j2與一個連接點j3(見圖2(d))。其中j1為推進劑流入節點，j2為流出節點。

彎頭的動力學方程可表示為[25]

(15)

式中：pj1,wj1,Aj1,Nj1,pj3,wj3,Aj3,Nj3分別為彎頭節點j1和j3的脈動壓強、重量位移、截面積和方向向量，rjde表示彎頭-可壓縮管的矢徑。

可壓縮管的動力學方程為[8]

(16)

(17)

KjdcAjdc1(Njdc1-Njdc2)wj3+KjdcAjdc1(Njdc2-

(18)

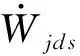
將式(15)～(18)聯立可得，彎頭-可壓縮管的動力學方程。

(1)動力學方程

(19)

Kjdcρg(Aj3Njdc1-Aj1Nj1)·rjde

(20)

(2)彎頭-可壓縮管對結構的作用力

考慮到彎頭對結構的作用力很小，建模過程中僅考慮可壓縮管部分對結構的影響，所以彎頭-可壓縮管對結構的作用力形式上與式(18)完全相同。

單元劃分后，對單元和節點進行編號，并以相同節點處脈動壓強相等作為連接條件，聯立相鄰單元的動力學方程。將聯立后的方程按照節點編號的順序對變量進行排序，并將其表示為矩陣形式，便得到不同工作模式下推進系統的動力學方程組[15]

(21)

(22)

(23)

式中：Mp,Cp和Kp分別為推進系統的質量矩陣、阻尼矩陣和剛度矩陣；S表示推力室脈動壓強對推進劑脈動重量位移的影響；w是節點脈動重量位移組成的狀態矩陣，維數等于節點個數；ptc是推力室脈動壓強組成的狀態矩陣，包含兩部分：氧化劑產生的脈動壓強ptco和燃料產生的脈動壓強ptcf，其維數等于兩倍的推力室個數；fps表示結構系統對推進系統作用的力矩陣；L為燃燒遲滯所產生的系數矩陣，而E表示脈動重量位移對脈動推力的影響；Xps表示結構系統單元與推進系統節點的映射關系，V0,V1和V2是組裝過程中形成的系數矩陣，Ф表示為火箭結構系統振型矩陣；q是結構廣義坐標組成的狀態矩陣，維數等于選取模態的個數。

1.2 結構系統動力學模型

結構的動力學方程為[15]

(24)

式中：Ms,Cs和Ks分別為火箭結構系統的模態質量矩陣、模態阻尼矩陣和模態剛度矩陣;fsp表示推進系統對結構系統作用的力矩陣

(25)

式中：Xf表示推進系統節點與結構系統單元的映射關系;Q0,Q1,Q2,Qp和U為推進系統作用力組裝后形成的系數矩陣;rp是推進系統單元的位移矢徑組成的矩陣。

1.3 POGO穩定性分析模型

聯立式(21)～(25)，可以得到動力冗余液體捆綁火箭POGO振動的狀態方程[15]，即

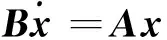
(26)

式中：

式中：Ew,Eq和Epc表示維數等于節點個數、選取模態數和兩倍推力室個數的單位矩陣。

2 算例分析

為研究蓄壓器能量值、泵增益和泵柔度對POGO穩定性的影響，定義如下特征阻尼比

ζc=min(ζi(t))

(27)

其中，ζi(t)表示POGO振動系統在t時刻的第i階阻尼比。當ζc>0，意味著POGO振動系統在任意時刻的各階阻尼比均大于零，不會發生POGO振動。但當ζc<0時，表明POGO振動系統在某時刻的某階阻尼比小于零，此時系統會發生POGO振動。ζc越大，最小阻尼比越大，POGO振動系統越不容易發生POGO振動。

2.1 蓄壓器能量值對POGO穩定性的影響

蓄壓器剛度為[8]

(28)

式中：P0V0為蓄壓器能量值，其余變量的定義與文獻[8]相同，這里不再累述。

通過增大P0V0可降低蓄壓器剛度，減小推進系統頻率。當推進系統頻率遠離結構系統頻率時，POGO振動不易發生。圖3給出芯級和助推蓄壓器P0V0的放大倍數βca和βba在設計值的0.2～5倍時，ζc的變化規律。

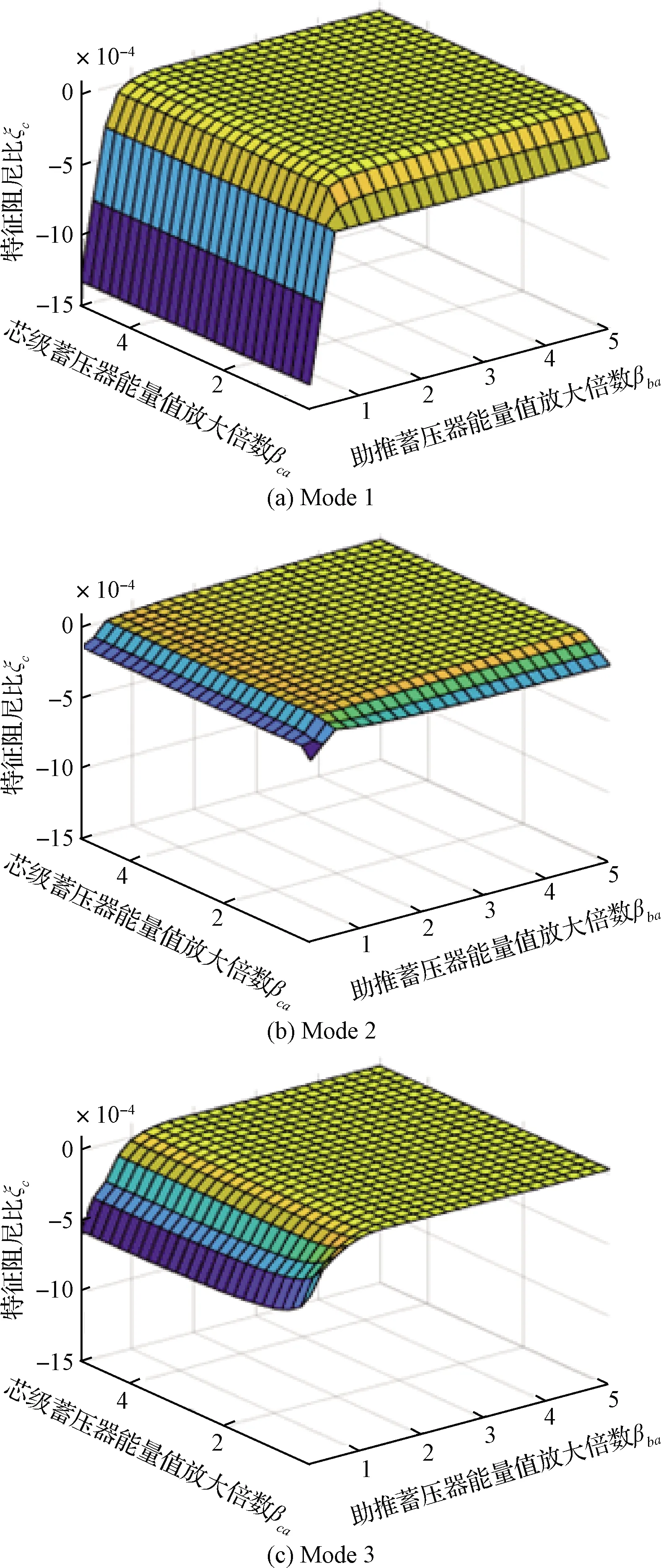
圖3 蓄壓器能量值對三種工作模式下液體捆綁火箭POGO穩定性的影響Fig.3 The effect of accumulator energy on POGO stability of liquid strap-on launch vehicle for three different working modes

圖3(a)顯示在Mode 1下，增大βca和βba可提高ζc，但當βca>0.8,βba>1.4時，ζc將穩定在2.5×10-5附近。這表明當推進系統和結構系統頻率相差較大時，P0V0的變化對POGO穩定性影響較小。此外，芯級蓄壓器P0V0對POGO穩定性的影響要弱于助推蓄壓器。這是因為助推貯箱和發動機的低階模態增益系數大于芯級貯箱和發動機的增益系數[26]，使得助推管路系統的流量脈動更容易造成POGO振動。Mode 2下ζc隨βca和βba的變化規律與Mode 1的結果基本相同(見圖3(b))，但最小的ζc為-2.1×10-4,大于Mode 1的-1.3×10-3，這得益于一臺助推發動機的故障。由圖3(c)可知，Mode 3模式下增大βba或降低βca可提高ζc，但當βca>1.2,βba>1.4時，ζc將穩定在3.4×10-5附近。此外，Mode 3下POGO穩定性對助推蓄壓器P0V0的敏感程度強過芯級蓄壓器。通過對比圖3(a)～圖3(c)發現，Mode 3下ζc隨βca和βba的最大變化量為2.2×10-4和6.0×10-4，大于Mode 2的1.5×10-4和1.7×10-4，小于Mode 1的3.2×10-4和1.4×10-3。因此，蓄壓器P0V0對Mode 1下的POGO穩定性的影響最大，Mode 2下的影響最小。這主要是由于交叉輸送管路聯通使Mode 2和Mode 3下推進系統頻率分布更為分散，變化更為復雜。

2.2 泵增益對POGO系統穩定性的影響

泵增益m+1的提高會增強推進系統和結構系統的耦合強度，對POGO穩定性造成不利影響[9]。圖4分析泵增益放大倍數βpg在設計值的1～3倍時，ζc的變化規律。

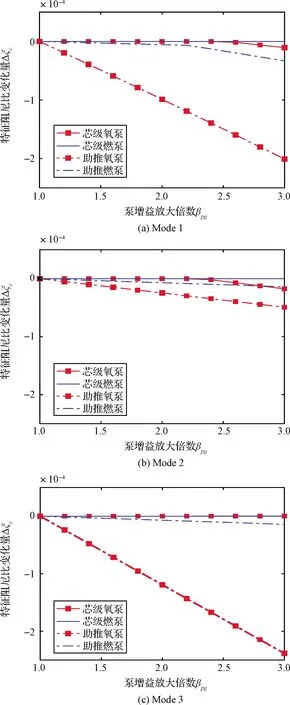
圖4 泵增益對三種工作模式下液體捆綁火箭POGO系統穩定性的影響Fig.4 The effect of pump gain on POGO stability of liquid strap-on launch vehicle for three different working modes

由圖4(a)可知，Mode 1下芯級氧化劑泵、芯級燃料泵、助推氧化劑泵和助推燃料泵的βpg的增大均會降低ζc，這與文獻[10]中的結論是一致的。此外，助推氧化劑泵的βpg由1增加至3，ζc減少2.0×10-4，大于助推燃料泵的3.3×10-5，芯級氧化劑泵的1.1×10-5，芯級燃料泵的8.0×10-15，這表明氧化劑泵的m+1對POGO穩定性的影響強于燃料泵，助推泵強于芯級泵，這種現象在Mode 2和Mode 3下也存在。燃路系統的阻尼和頻率一般高于氧路系統，而且氧路系統的頻率更接近結構低階頻率，這會造成氧泵的變化對POGO穩定性的影響更明顯。文獻[10]指出耦合強度與m+1和模態增益系數的乘積呈正相關，因此具有較大模態增益系數的助推泵的影響強過芯級泵。通過對比圖4(a)～圖4(c)發現Mode 1下助推氧化劑泵的βpg由1變化至3，ζc減少2.0×10-4，大于Mode 2的4.9×10-5，略小于Mode 3的2.4×10-4。這表明Mode 1和Mode 3下助推氧化劑泵的m+1對POGO穩定性的影響比Mode 2更加靈敏，這是由于Mode 2下一臺助推發動機的停機會減弱耦合強度，使得助推氧泵的m+1的影響變小。

2.3 泵柔度對POGO系統穩定性的影響

泵柔度Cpu的增大會降低推進系統頻率，進而影響POGO穩定性。圖5分析泵柔度放大倍數βpc在設計值的0.5～1.5倍時，ζc的變化規律。

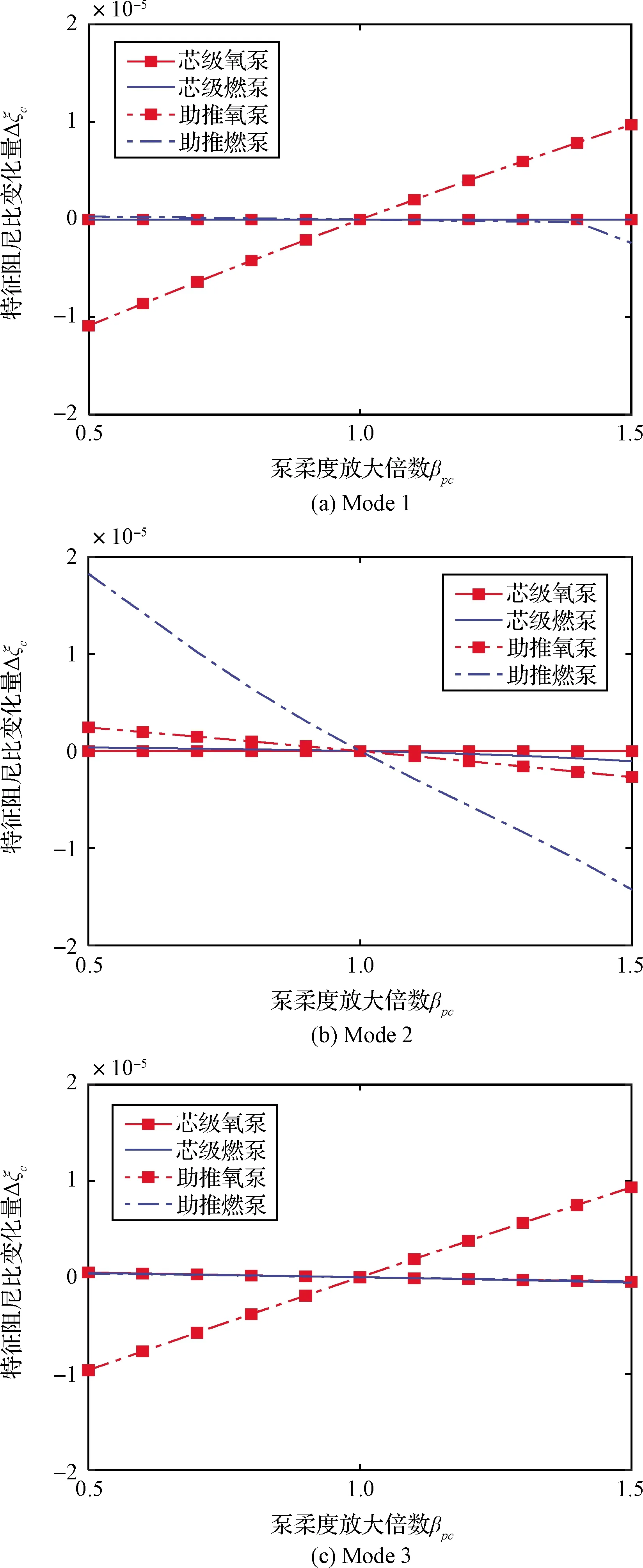
圖5 泵柔度對三種工作模式下液體捆綁火箭POGO系統穩定性的影響Fig.5 The effect of pump flexibility on POGO stability of liquid strap-on launch vehicle for three different working modes

圖5顯示三種工作模式下芯級氧化劑泵的βpc由0.5增加至1.5，ζc幾乎不改變，這意味著芯級氧化劑泵Cpu對POGO穩定性的影響較小，這是由于較小的芯級模態增益系數減弱了芯級氧化劑泵對POGO穩定性的敏感程度。助推氧化劑泵的βpc由0.5變化至1.5，Mode 1和Mode 3下ζc增加2.1×10-5和1.9×10-5，Mode 2減少5.1×10-6，這表明Mode 1和Mode 3下助推氧化劑泵Cpu的影響大于Mode 2。氧化劑泵Cpu和蓄壓器P0V0都是通過改變氧路系統頻率，影響POGO穩定性，因此ζc隨氧化劑泵Cpu的變化規律與蓄壓器P0V0的影響是基本一致的。助推燃料泵的βpc的增大會降低ζc，其中Mode 2下降低3.3×10-5，大于Mode 1和Mode 3的2.7×10-6和8.0×10-7，也就是說助推燃料泵Cpu的影響在Mode 2下最大，這是因為燃路系統的頻率較高，通常比結構的低階頻率高，當燃路系統頻率下降時可能會接近結構頻率，誘發POGO振動。同時不同工作模式下推進系統頻率分布規律相差較大，這影響特征阻尼比對助推燃料泵Cpu的靈敏度。

3 結 論

本文利用改進的Rubin建模方法，建立了獨立工作、一臺助推發動機故障助推貯箱向芯級發動機供給推進劑和兩助推器同時向芯級發動機供給推進劑三種工作模式下，液體捆綁火箭POGO穩定性分析模型。利用QR分解法求解該分析模型，研究POGO穩定性，得到如下結論：

1) Mode 1和Mode 3下，POGO穩定性對助推蓄壓器能量值的敏感程度強過芯級蓄壓器。Mode 1下蓄壓器能量值對POGO穩定性的影響最強，而Mode 2下蓄壓器能量值的影響最弱。

2) 三種工作模式下，泵增益的提高均會減弱POGO穩定性，其中氧化劑泵的影響強于燃料泵，助推泵的影響強于芯級泵。Mode 1和Mode 3下泵增益對POGO穩定性的影響比Mode 2更加靈敏。

3) 三種工作模式下，芯級氧化劑泵柔度對POGO穩定性的影響較小。Mode 1和Mode 3下助推氧化劑泵柔度的影響大于Mode 2。助推燃料泵柔度的增大會降低燃路系統頻率，可能誘發POGO振動，其中Mode 2下的影響最大。