空間繩網旋轉展開動力學分析

秦志偉，劉 振，孫國鵬，祁玉峰

(1. 哈爾濱工業大學機械工程系，哈爾濱 150001；2. 北京空間飛行器總體設計部，北京 100094)

0 引 言

隨著人類對太空的探索，大量衛星被送入太空，這個過程累積的拋棄物、火箭爆炸物等嚴重污染著太空環境，已經失效的衛星或碎片相互撞擊又將產生更多的碎片，這些碎片的平均軌道速度為7 km/s至13 km/s，與航天器的平均撞擊速度達10 km/s，一旦發生撞擊事故，將導致航天器損毀，是空間在軌衛星、空間站嚴重的潛在威脅[1-2]。因此，針對空間碎片的主動捕獲及銷毀技術的研究尤為重要[3]。而繩網捕獲相比于對接式抓捕和機械臂抓捕等剛性捕獲方式具有收攏空間少、誤差冗余大、安全性高等優點，在非合作特征顯著的空間廢棄衛星等抓捕中有著重要的應用需求[4]。

鑒于此，2001年，歐空局(ESA)提出了用于抓捕地球靜止軌道廢棄衛星，并將其轉移到墳墓軌道的ROGER計劃[5]。2018年9月，英國薩里航天中心(SSC)首次通過衛星直接彈射儲存艙內的繩網進行了捕獲空間碎片的在軌實驗[6]，驗證了空間繩網捕獲方式的可行性。瑞典皇家理工學院(RIT) G?rdsback等應用商業軟件MATLAB和LS-DYNA對基于中心轂輪旋轉展開的繩網模型進行了無控展開和受控展開的動力學研究[7-8]。瑞士斯德哥爾摩皇家理工學院(KTH)進行了名為“Suaineadh”的太空測試實驗以驗證該類旋轉展開方案[9]。國內對于空間繩網展開的研究起步較晚，但也進行了許多有益的探索。北京航空航天大學趙國偉等[10]基于商業軟件LS-DYNA對網體展開過程中的繩體材料的拉伸和回復過程進行了數值模擬。哈爾濱工業大學張越等[11]設計了一種四角質量塊發射角度可調的“彈拋式”捕網發射系統，增加了發射的可靠性。國防科學技術大學張青斌等[12]對繩網系統展開動力學特性進行了天地差異性分析，通過與地面實驗的校驗來反推太空環境下繩網展開的運動狀態；文獻[13-14]設計了一種空間飛網的二級發射展開方式，增加了網體拋出的可靠性；陳青全等[15]采用定力撕裂帶對繩網網型進行了控制研究。文獻[16-17]基于商業軟件ABAQUS和自編程序THUsolver對直接彈射拋出的網體展開過程進行了參數分析和優化。文獻[18-19]針對空間繩網捕獲系統建立了收口階段質量塊的動力學模型，并對繩網系統的收口機構進行了設計和優化。

對上述文獻進行分析發現，文獻[4,10-17]采用直接拋射網體展開方案，火工裝置發射時存在對發射平臺沖擊大、展開后繩網網型維持時間短等問題；文獻[7-9]為基于中心轂輪旋轉展開方案的分析和實驗，實現該方案的控制過程復雜且難以保證展開的有效性；文獻[18-19]提出的收口形式可作為繩網展開后實現收口作業系統設計的重要參考。本文提出了一種基于周置可控旋筒的旋轉展開空間繩網系統方案；利用拉格朗日動力學方程構建了網臂解析模型，采用MATLAB、ABAQUS軟件構建了網臂/網體有限元仿真模型并進行了模型間的仿真對比校驗；最后基于網體有限元仿真模型對繩網網型、旋筒控制策略進行了優化分析。

1 空間繩網系統的旋轉展開方案

本文提出的基于周置可控旋筒旋轉展開的網體卷繞方案如圖1所示，圖1(a)～圖1(d)為網體的折攏過程。與文獻[7]中基于中心轂輪旋轉展開方案的折疊過程類似，正方形的空間網體沿四邊中心線呈“N字形”聚攏到繩網中心形成空間網臂，為保證網體有序展開，折攏過程中網體外邊始終在最外側。將四個網臂分別按順時針(逆時針)卷繞在四個旋筒上，限制四個旋筒的相對位置實現網體的預先收攏，如圖1(e)～圖1(f)所示。

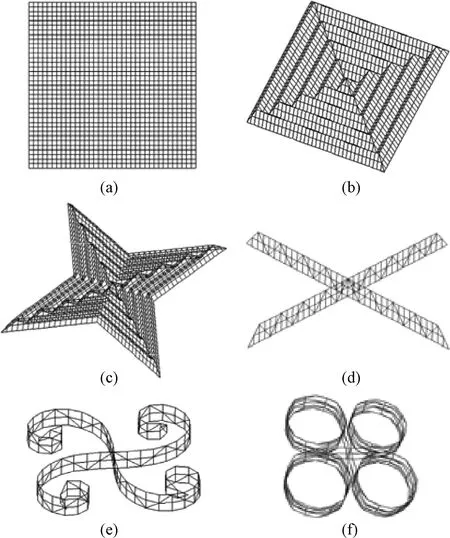
圖1 網體折疊和卷繞過程Fig.1 Space web folding and rolling sequence

空間繩網系統的旋轉展開過程可視為上述卷繞過程的逆過程，空間繩網實現捕獲操作的具體過程如下：

1) 起旋階段，旋筒及纏繞其上的網體以相同的角速度旋轉。

2) 釋放階段，將旋轉狀態的空間繩網系統以一定初速度彈出。

3) 解鎖階段，繩網系統彈出后經預設時間后，限位機構解鎖，同時旋筒內的控制系統啟動，四個旋筒此時具有相同大小的角速度和平動速度。

4) 展開階段，四個旋筒帶動纏繞其上的網體有序展開并維持一定時間。

5) 捕獲階段，當網體包覆非合作目標后，收口機構實現網體收口。

2 空間繩網系統的模型構建

卷繞收攏的網體在旋轉展開過程中，相同時刻下網體不同區域的質量和速度難以直接描述，構建網體解析模型較為困難，但由文獻[7-8,10,16-17]可知,有限元仿真是模擬繩網展開動力學過程的有效手段。因此，本節首先構建出具有相同工作過程的網臂解析模型；在ABAQUS/Explicit仿真環境下，通過對網體折攏后中心約束區域自由度的不同定義構建出網臂/網體旋轉展開有限元仿真模型(見圖2，網臂有限元仿真模型的中心區域綁定約束，網體有限元仿真模型中心區域無約束)，對比分析上述三種模型以檢驗有限元仿真模型的有效性。

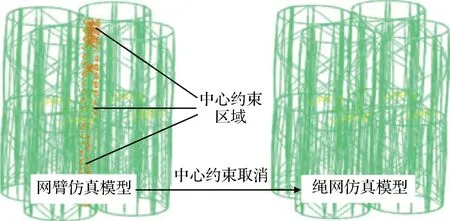
圖2 網臂模型與網體模型的關系Fig.2 The relationship between arms and webs

2.1 基于拉格朗日動力學方程的網臂解析模型

網臂解析模型構建的假設如下：

(1) 四個旋筒視為理想勻質筒狀殼體。

(2) 網臂視為有質量、無厚度的直線。

(3) 網臂的線密度從繩網中心到外側與旋筒的固定端線性減小。

(4) 旋筒和網臂始終在垂直于旋轉軸的平面內運動，忽略網臂在展開平面外的波動。

(5) 忽略網臂與自身的內摩擦、網臂與旋筒間的摩擦耗能。

(6) 四個旋筒及卷繞在其上的網臂在展開過程中呈中心對稱狀態。

根據假設(6)，取其中一條網臂進行分析。選擇旋筒轉角θ和網臂卷繞角φ作為系統的廣義坐標，建立如圖3所示的動力學分析模型，其中固定坐標系為O0-x0y0z0、平動坐標系為O1-x1y1z1、網臂旋出切點處的動坐標系為O2-x2y2z2。以R和r表示旋筒的幾何中心相對于定坐標系O0-x0y0z0和動坐標系O2-x2y2z2的位置矢量，L表示動坐標系原點O2相對于定坐標系原點O0的位置矢量。

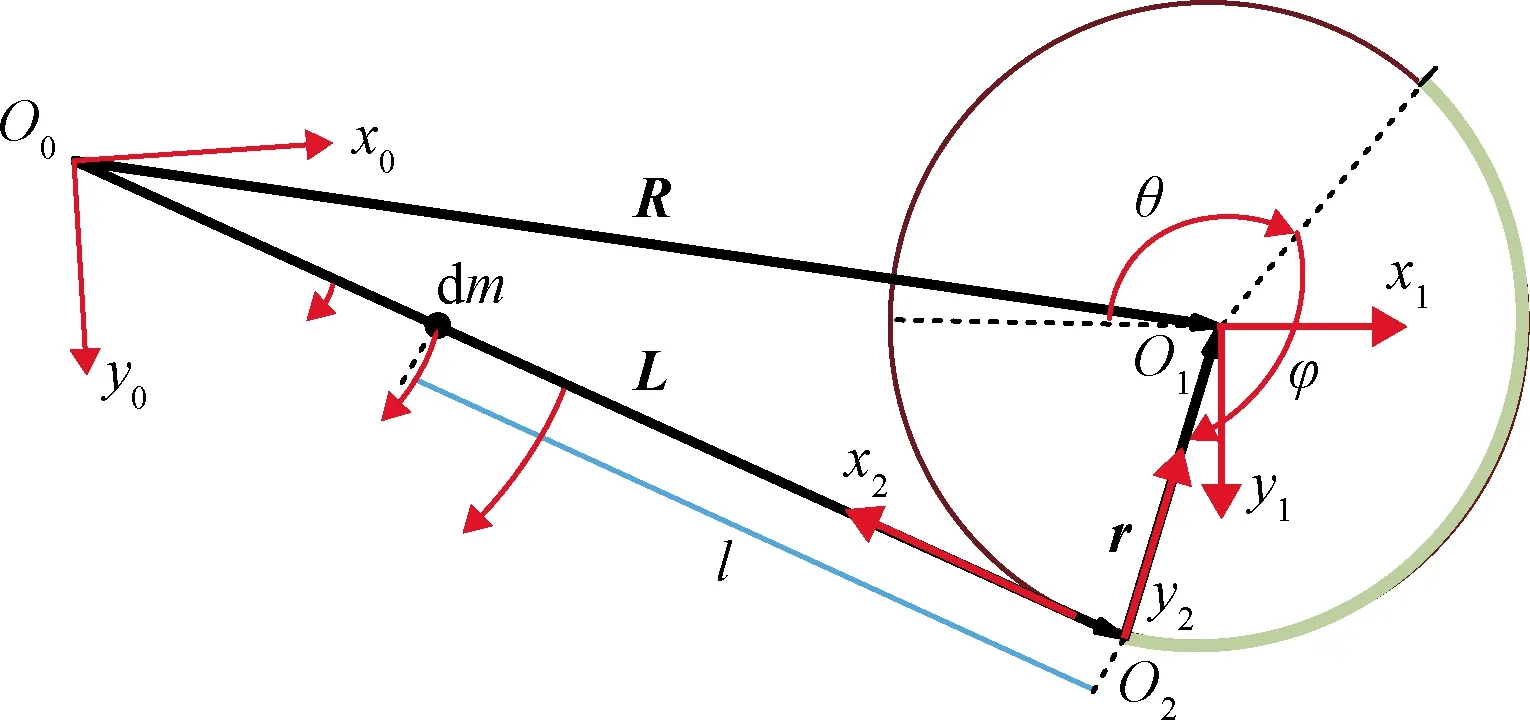
圖3 旋轉展開分析模型Fig.3 The analytical model based on rotation

根據矢量關系

R=L+r

(1)

對式(1)等號兩邊求導可得

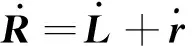
(2)

根據假設(1)，四周旋筒相對于各自旋轉軸的轉動慣量J為

J=mhr2

(3)

式中：mh為旋筒質量，r為旋筒半徑。

根據網臂的展開方式，網臂的旋出長度L為

L=Lmax-rφ

(4)

(5)

式中：S為繩網邊長，Lmax為網臂旋出的最大長度。

根據假設(3)，網臂上任意繩段微元dm處的線密度ρl為

(6)

式中：mw為繩網質量，n為旋筒個數，l為任意繩段微元dm與動坐標系原點O2間的距離。

系統總動能EK由仍卷繞在旋筒上的網臂的動能EK1、已經旋出的網臂的動能EK2、旋筒的動能EK3三部分組成，整理為

(7)

由總動能列寫第二類拉格朗日方程

(8)

其中，

(9)

式中：Ff為作用在四個旋筒上的控制力矩之和。

(10)

2.2 基于中心差分算法的有限元仿真模型(FEM)

本文采用ABAQUS/Explicit構建繩網有限元模型，仿真模型的建立過程如下：

1) 根據網體初始折疊方式(見圖1)，通過MATLAB軟件編程輸出繩網部件中單元的節點連接關系和節點的三維坐標，直接構建出繩網部件的網格模型。繩索單元的節點連接關系可由網目內單元分段數(a)、繩網網目數(b)描述，如圖4所示。

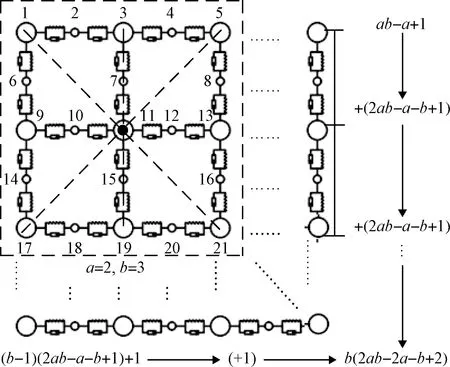
圖4 繩網仿真模型節點序號排布定義Fig.4 The arrangement of nodes in the FE web models

2) 將預先定義的正交叉狀的折疊繩網模型導入ABAQUS/CAE界面中，采用殼單元創建旋筒部件，旋轉平移四周旋筒，使繩網緊密卷繞在四個旋筒上，得到初始裝配誤差很小的裝配體(誤差來源于軟件的接觸識別精度)，構建過程如圖5所示。

圖5 系統裝配模型的構建過程Fig.5 The construction process of the assembly model

3) 通過導入*odb的方式輸出上述裝配關系，重新設置材料屬性、接觸關系、約束條件、預定義場(初速度)等仿真條件，輸出inp文件。

4) 采用FORTRAN語言編寫VUAMP子程序，實現對旋筒控制力矩的加載。

5) 提交inp文件和子程序進入求解器進行網臂/網體旋轉展開動力學分析，軟件基于中心差分算法求解動力學平衡方程[16]：

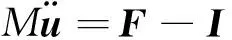
(11)

2.3 解析模型與有限元模型的仿真對比分析

本文算例的仿真參數如表1所示。

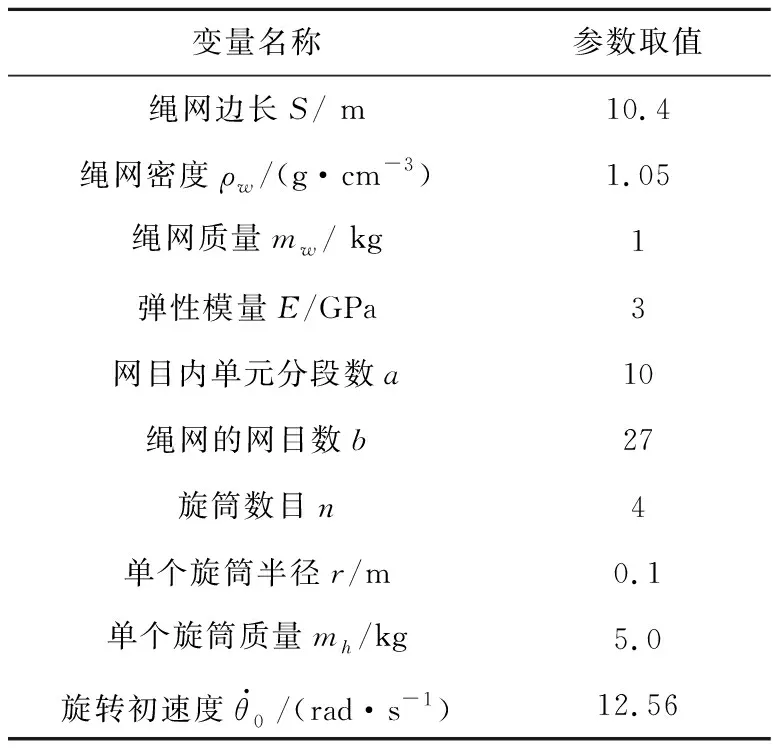
表1 系統仿真參數Table 1 Simulation parameters of system

采用電機-反作用飛輪的機構實現方式進行控制，控制律初選為

(12)

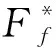
選取旋筒角速度和網臂旋出長度作為模型間對比的特征變量，旋筒角速度表征網臂/網體及作用在旋筒上的控制力矩對旋筒的影響，有效的控制使網臂/網體展開后角速度在零值附近；旋出長度評價網臂/網體的展開程度，旋出長度越大，展開越充分(為統一對比，繩網模型中旋出長度的定義與網臂模型相同)。通過對網臂解析模型的預先仿真計算得出，當T=267 N·mm時，網臂可完全展開并實現有效的控制，將該幅值引入網臂/網體有限元仿真模型中，得到的展開過程如圖6、圖7所示。

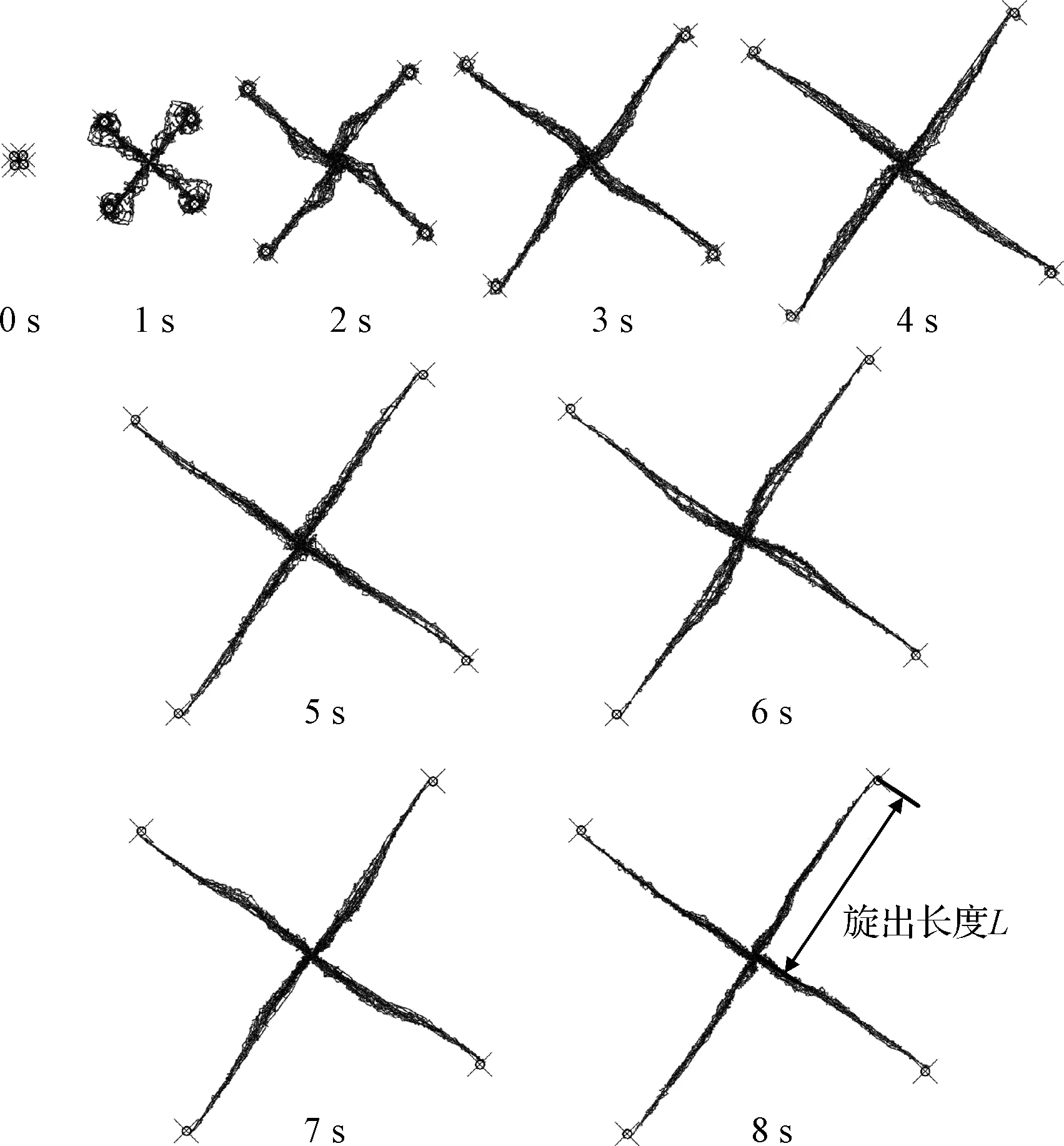
圖6 控制力矩作用下網臂展開過程(等比縮放)Fig.6 Controlled deployment of arms (proportional scaling)

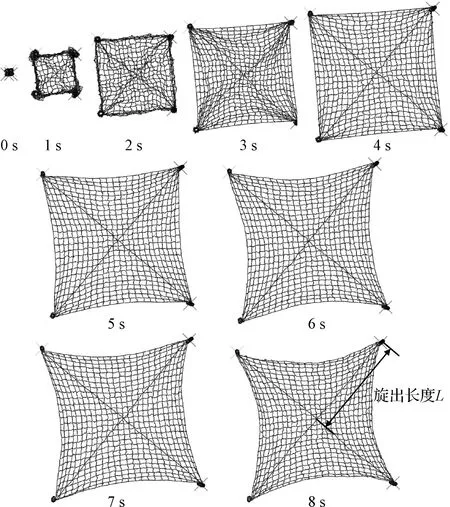
圖7 控制力矩作用下網體展開過程(等比縮放)Fig.7 Controlled deployment of webs (proportional scaling)

由圖8、圖9可知，在控制力矩作用下，網臂解析模型和網臂有限元仿真模型的旋筒角速度、網臂旋出長度具有高度的一致性，對比驗證了有限元仿真模型的有效性。將網臂有限元仿真模型中心約束取消變為網體有限元仿真模型后，由于兩個模型在展開過程中的旋筒最大位移半徑和繩網部件內部傳力形式的不同，致使兩個有限元仿真模型的旋筒角速度和網臂旋出長度存在差異。

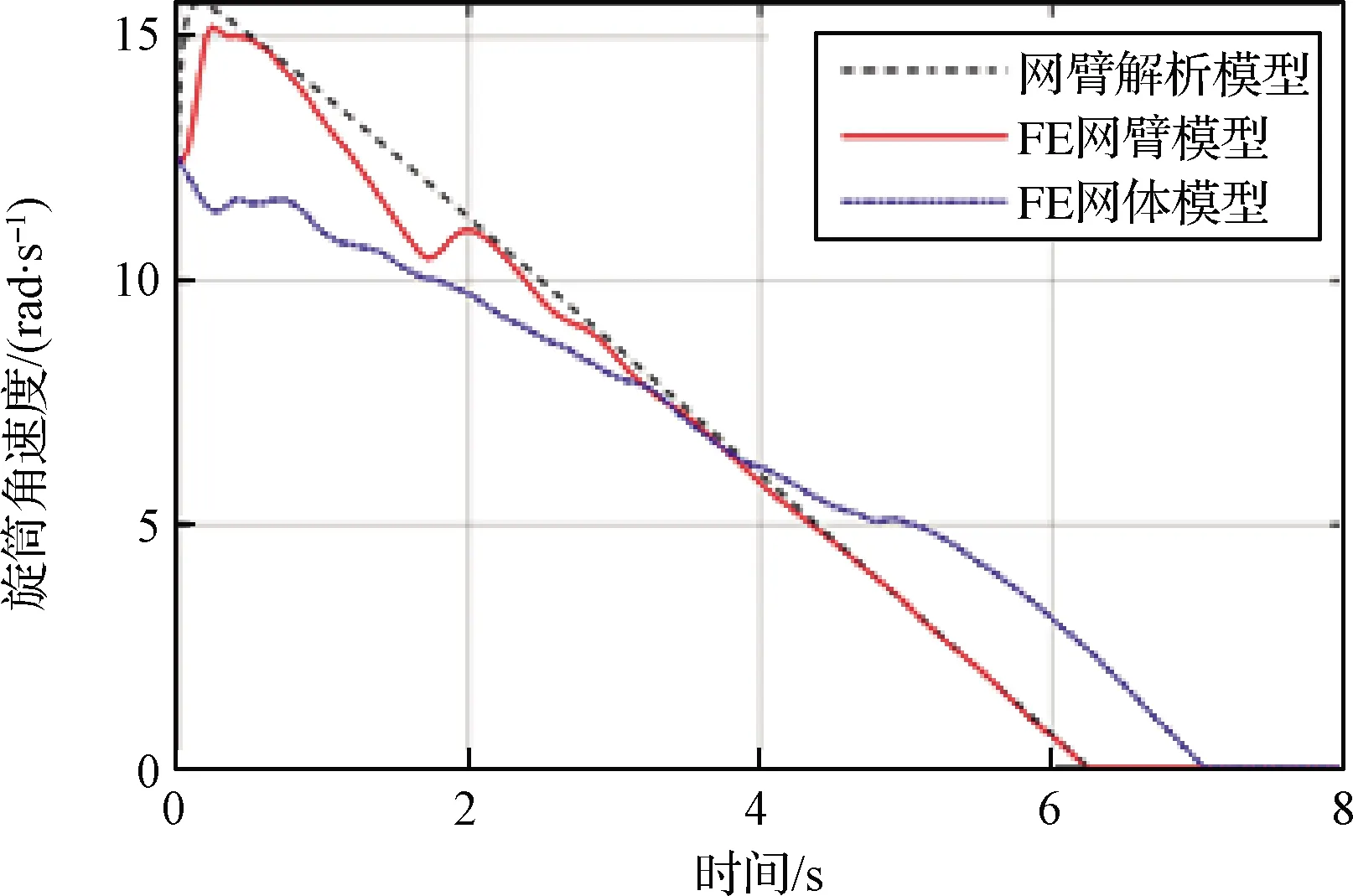
圖8 控制力矩作用下的旋筒角速度Fig.8 The angular velocity of the rotary tubes under control

圖9 控制力矩作用下的網臂旋出長度Fig.9 The length of the arms under control

3 空間繩網網型及展開控制策略優化分析

3.1 空間繩網網型優化

在繩網旋轉展開過程中，定義每條網邊中心點連接形成的正方形區域為有效捕獲區域，其面積即為有效捕獲面積；繩網其余邊角部分為無效捕獲區域，該區域無法對非合作目標進行有效攔截捕獲。考慮到實際操作中繩網與旋筒間的綁定連接以及網體在展開過程中有效捕獲區域的維持，設計如圖10所示的五種網型備選方案(圖中為旋轉展開過程中的繩網網型狀態)。方案一在繩網四角各延伸一截繩段，方便旋筒與網體的綁定連接；方案二至方案五為在方案一基礎上增加四種系繩牽拉傳力方式。五種方案所用網體邊長均為10.4 m，周置旋筒以相同的初始角速度(12.56 rad·s-1)共同旋出且保持該角速度勻速旋轉。

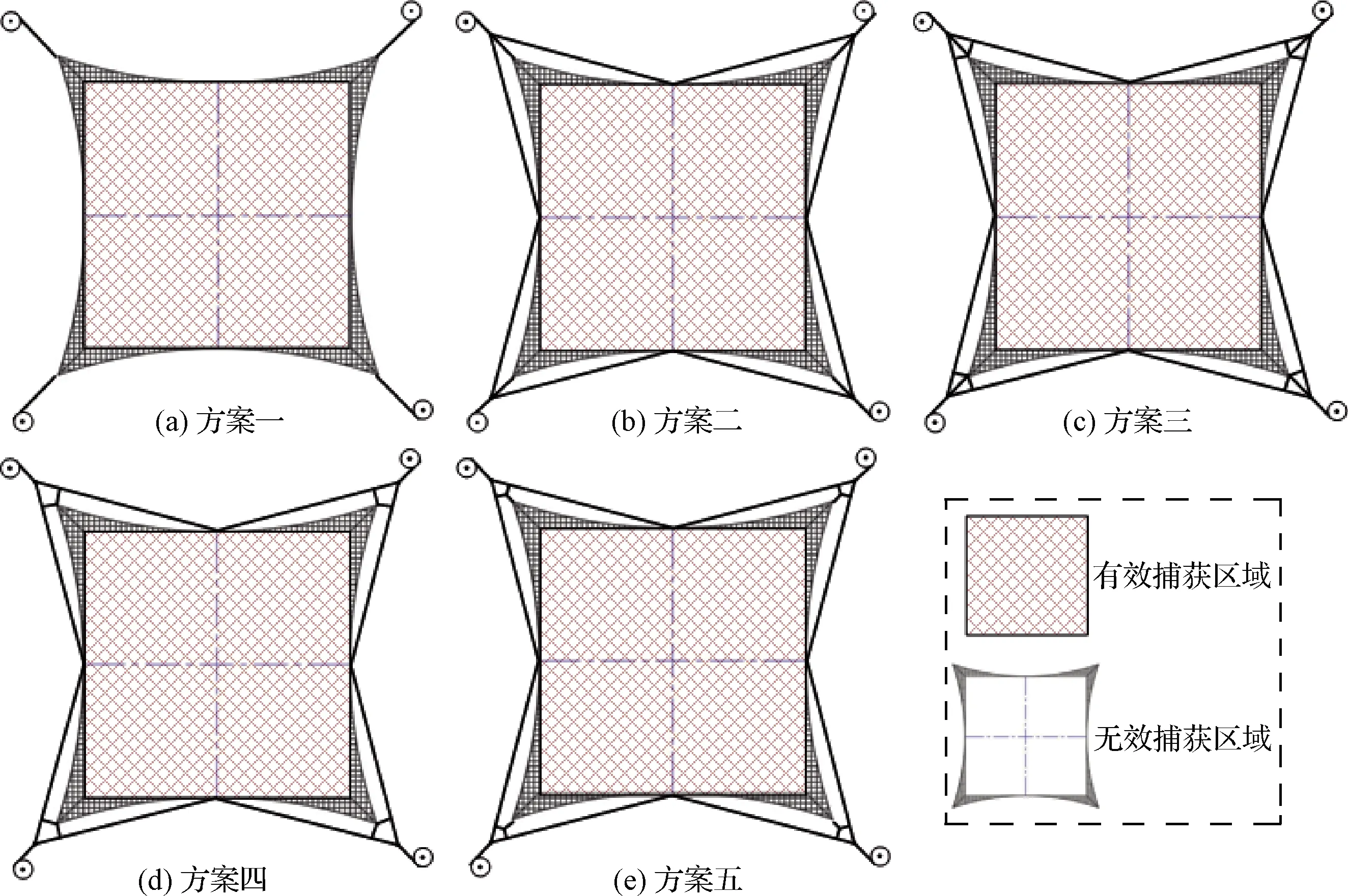
圖10 繩網網型優化方案Fig.10 The optimization of the web topology

圖11為在上述過程中，不同方案下的有效捕獲面積對比曲線。在繩網展開初期(0 s～3 s)，五種構型方案下的有效捕獲面積變化沒有明顯差別；而在展開后期(3 s～5 s)，構型方案三在展開過程中的有效捕獲面積維持較高且波動幅值變化最小，故以下研究均在構型方案三的基礎上展開。

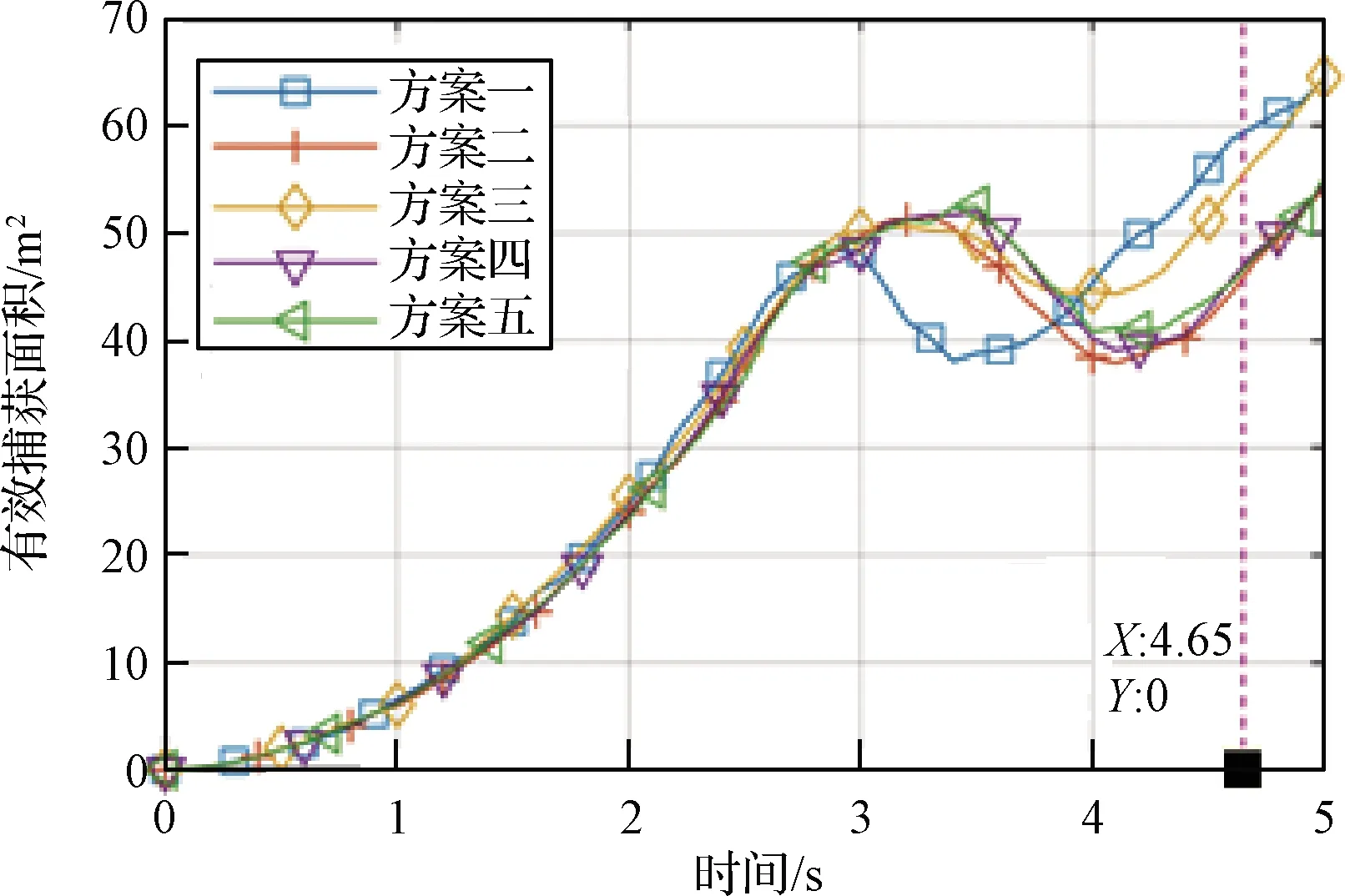
圖11 不同方案下的有效捕獲面積對比Fig.11 Comparison of effective capture area in different cases

3.2 繩網系統旋轉展開控制策略優化

在仿真模型中引入控制律(12)進行分析，當控制力矩幅值T=220 N·mm時，繩網剛好完全展開且實現了有效的控制(繩網展開后旋筒角速度為零)，控制力矩加載曲線如圖12所示。繩網尚未完全展開時，電機的輸出控制力矩為定值；繩網完全展開后，控制力矩呈頻繁的正負往復波動狀態。力矩的頻繁波動表明此階段控制力矩幅值設置的不合理，因這種控制狀態較為耗能，為此設計了三種分步加載控制策略。

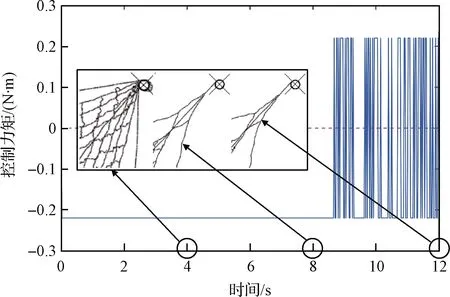
圖12 控制力矩波動變化Fig.12 The fluctuations of control torque

策略一為當角速度尚未衰減至零時，以一恒定力矩T控制，當傳感器監測到旋筒角速度衰減到零后，電機控制力矩置為零，控制律如式(13)所示。

策略二為當角速度尚未衰減至零時，以一恒定力矩T控制，當旋筒角速度首次衰減到零后，改用一個較小的控制力矩T1控制，控制律如式(14)所示。

(13)

(14)

策略三為當旋筒角速度尚未衰減至零時(定義狀態標記為Δ=1)，采用較大控制力矩T控制，當旋筒角速度首次衰減到零后(定義狀態標記為Δ=2)，電機的輸出力矩在較小的范圍內(-T1,0)波動控制，控制律如式(15)所示。

(15)

采用上述三種分步加載控制策略修正式(12)，得到控制力矩的加載情況如圖13所示，有效捕獲面積的變化曲線如圖14所示。比較有效捕獲面積的控制效果，策略一的控制效果較差，策略二和策略三的控制效果與原方案大致相同，但卻有效地減少了控制力矩的波動幅度和頻率。

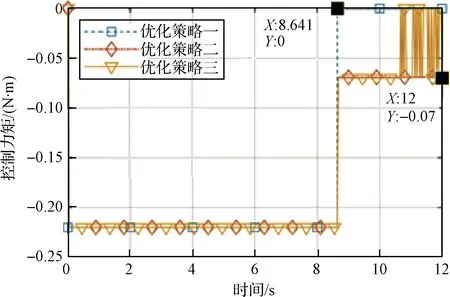
圖13 三種加載控制策略Fig.13 Three loading strategies for controlling torque

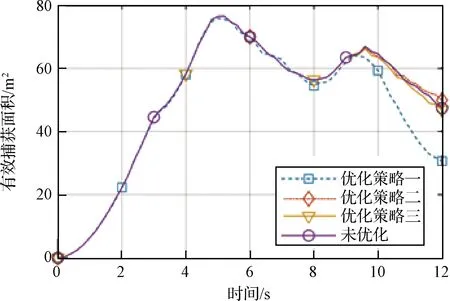
圖14 不同控制策略下的有效捕獲面積Fig.14 Effective capture area under different control strategies

因策略二形式上的簡單性，若能通過實驗尋找到第二步控制力矩加載的時間和幅值，則可直接采用計時器代替基于旋筒角速度的力矩控制，避免了傳感器的引用，降低了控制成本和實現難度。繩網系統在策略二控制下的展開過程如圖15所示，選取旋筒中心和網邊中心為參考點，兩參考點距網體中心的距離半徑變化如圖16所示。

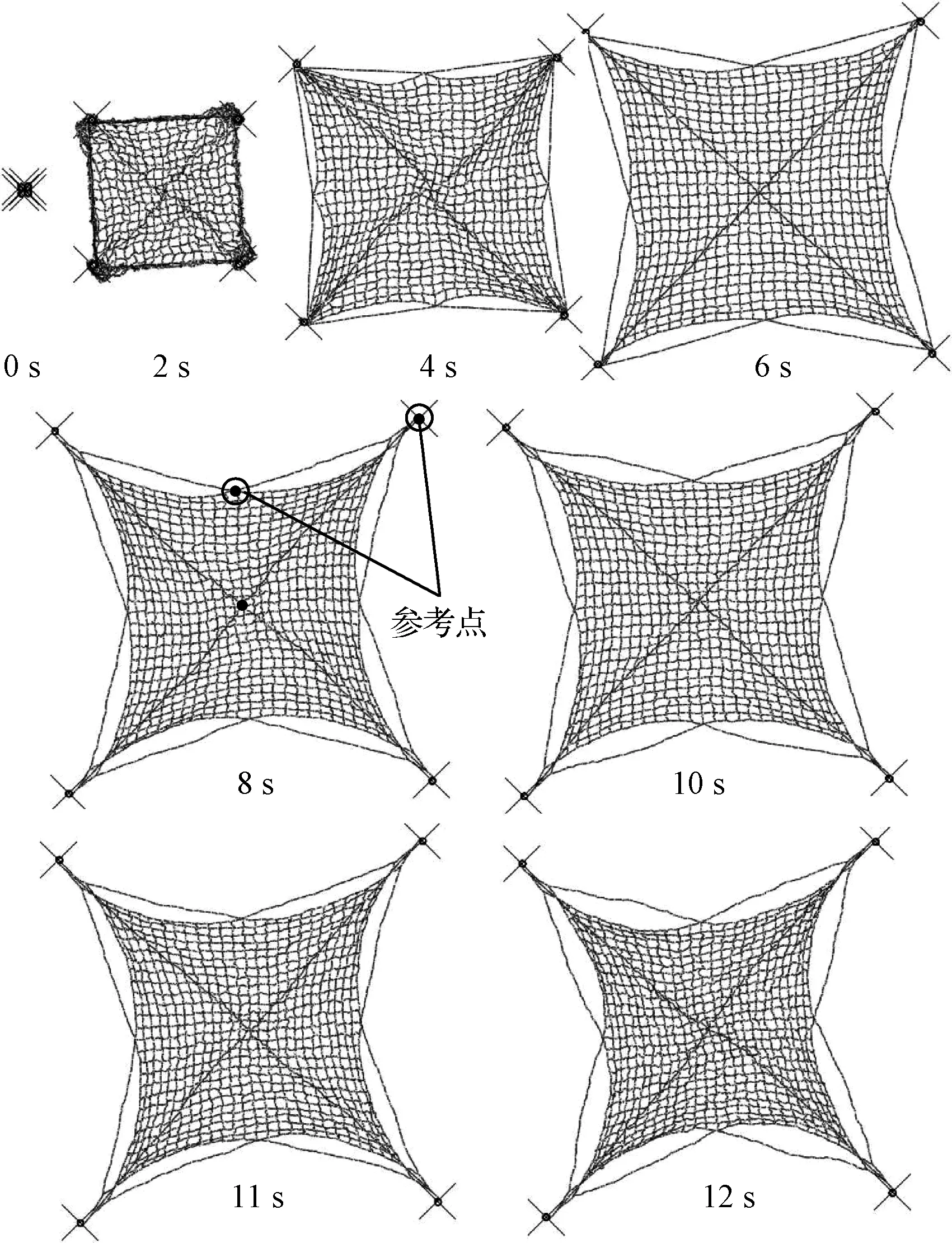
圖15 構型優化后的受控展開(等比縮放)Fig.15 Controlled deployment of the structural webs after optimized (proportional scaling)

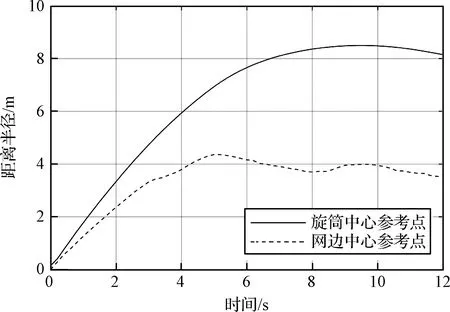
圖16 參考點與網心的距離Fig.16 The distance between reference points and web center

在旋筒與網體邊沿間系繩的牽拉傳力作用下，邊心與網心的距離在5 s左右達到峰值，此時亦為有效捕獲面積的峰值；隨著旋筒繼續外旋，系繩牽拉綁定結構使邊心-網心距具有較小的波動幅度；由于旋筒在繩網完全展開時仍有少量殘余平動動能，當旋筒-網心距離達到峰值時，邊心-網心距同樣出現第二次小高峰，之后網體“回彈”，兩參考點距網體中心的距離緩慢減少。

定義有效捕獲面積達最大展開面積的60%時，可適用于捕獲任務[15]；繩網從初始解鎖釋放到展開達最大展開面積的60%時所用的時間為展開時間，適用于捕獲任務的時間為捕獲時間。將本文算例的仿真結論與文獻[12,15-16]中采用“直接彈拋”展開形式的仿真結論(由繩網展開曲線獲得)對比匯總如表2所示，采用本文的旋轉展開方案，繩網展開時間相對較慢，但卻有效地減緩了網體的“回彈”過程，捕獲時間大幅增加，提升了捕獲性能。

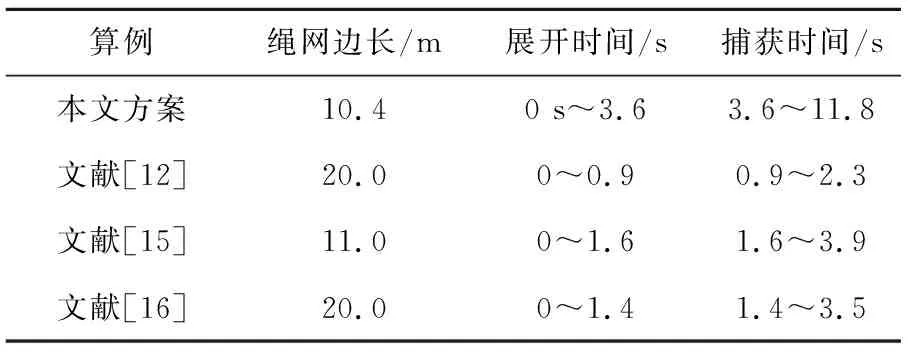
表2 不同算例的結論對比Table 2 Comparison of conclusions of different samples

4 結 論

本文提出了一種基于周置可控旋筒的旋轉展開空間繩網系統方案，采用拉格朗日動力學解析模型和基于中心差分算法的有限元仿真模型對繩網展開過程的動力學特性進行了對比分析，旋筒的角速度、網臂的旋出長度在不同模型的求解下均表現良好的一致性，說明了有限元模型的有效性。

對繩網網型和旋轉展開控制策略的優化分析表明：采用系繩同時牽引網體四角及網邊中心的構型(方案三)時，繩網在旋轉展開過程中有效捕獲面積的波動幅度最小；采用分步加載的控制策略，在有效減小控制力矩的波動幅度和頻率的基礎上進一步確定便于工程實現的旋筒控制策略(策略二)；相較采用“直接彈拋”形式展開空間繩網，基于周置可控旋筒的旋轉展開實現了更長時間的空間保形。