人工智能氣動特性預測技術在火箭子級落區控制項目的應用

杜 濤，許晨舟，王國輝，宮宇昆，何 巍，牟 宇，李舟陽，沈 丹，程 興，高家一，韓忠華

(1. 北京宇航系統工程研究所，北京 100076；2. 西北工業大學航空學院翼型、葉柵空氣動力學重點實驗室，西安 710072)

0 引 言

氣動特性的預測是飛行器氣動設計的核心工作之一。高超聲速飛行器流動復雜，建立覆蓋飛行包線的氣動特性數據庫通常需要開展規模龐大和復雜的風洞試驗和計算流體力學(Computational fluid dynamics，CFD)計算，成為影響研制經費和進度的重要因素。

20世紀80年代之前，飛行器研制的氣動特性預測主要依靠風洞試驗，重要項目的試驗量近乎天文數字，給研制成本和進度控制造成巨大壓力。得益于計算機技術的發展，CFD進入工程領域，降低了研制對風洞試驗的耗費。20世紀90年代后，一系列外界因素的改變促使工業部門意識到，需要發展更高效的氣動數據庫建立技術，降低研制成本并縮短周期。這成為飛行器設計領域活躍的研究方向。經過近30年的發展，已在下述三個方面取得長足進步。

1)預測中心從“數據”轉移到“知識”

傳統OFAT(One factor at a time)方法[1]，以“數據”為中心，試驗規模與需求之間是線性關系。以現代試驗設計(Modern design of experiments, MDOE)[2-3]為代表的新方法，以氣動特性的“知識”和“關系”為中心，取代數據本身。當氣動設計人員判斷模型精度滿足要求，風洞試驗即可結束。蘭利研究中心研究表明，采用MDOE策略，試驗量減少了80%，風洞占用時間縮短了50%[2]。

2)氣動數據融合技術

氣動數據融合是指將不同來源、不同精度的氣動數據，整合為一組高精度的氣動數據集的方法。NASA在2014年發布的報告中曾指出[4]：“開展針對飛行試驗、風洞試驗和CFD方法的氣動數據融合，可以快速、準確地預測飛行器氣動特性，對指導風洞試驗關鍵工況的選取具有重要意義。”

這一領域最有代表性的技術是可變精度方法[5](Variable fidelity model, VFM或Variable complexity model, VCM)。該方法最早是Dudley等[6]于1995年在NASA高速民用運輸機研究計劃中發展出來。Da Ronch等[7]運用變可信度代理模型方法，發展了一個用于飛行模擬的氣動數據模型。Navarette等[8]提出采用基于徑向基函數(RBFs)的神經網絡方法實現不同來源氣動數據的融合。2003年，在第二代LGBB(Langley Glide Back Booster)飛行器的氣動數據庫建立中，提供了一個數據融合技術工程實踐范例。借助數據融合技術，在規定的一周時間內，高精度的粘性解僅占不到10%[9]。

3)人工智能預測技術

1985年，Tong[10]首次提出將人工智能技術應用于氣動設計。隨后，線性回歸、支持向量機、貝葉斯模型和神經網絡等機器學習算法得到發展，應用于氣動數據預測[11-13]。機器學習，是指通過數據訓練出能完成一定功能的模型，是實現人工智能的手段之一，也是目前最主流的人工智能實現方法。Marques等[14]采用監督學習的方法對超過1550個翼型的氣動數據進行建模。Yilmaz等[15]利用深度卷積神經網絡(CNN)從非結構的數據中對翼型的性能進行預測，預測結果的準確性超過80%。Bouhlel等[16]利用梯度增強的人工神經網絡實現了亞、跨聲速區翼型氣動特性的快速預測。陳海等[17]以翼型圖像作為輸入，建立了CNN模型來預測翼型的氣動系數。

但是，目前人工智能預測的研究工作，其氣動數據規模較小，特性簡單，缺少多維復雜數據的應用研究，更缺乏結果正確性的評估[18]。綜合分析,技術成熟度仍處于實驗室研究階段，目前未見在工程項目設計應用的文獻報道。

中國西昌等火箭發射場地處內陸腹地，火箭的一子級殘骸往往墜落在內陸地區。隨著社會的快速發展，落區人口日益密集，亟需采取措施降低發射任務對落區居民生產和生活的影響。對火箭殘骸的落區控制早期采取預測殘骸散布的被動控制[19]，當前以發展減少火箭殘骸數量[20]或可控返回[21]的主動控制為主。由于內陸落區不具備回收條件，因此開展現役火箭的縮小落區范圍研究更有現實意義。

本研究團隊承擔了現役運載火箭一子級落區精確控制的研制工作。在火箭一子級級間段增加四片柵格舵(外形見圖1)，精確控制殘骸落點。柵格舵的優點是可折疊，對上升飛行段的影響小，鉸鏈力矩也小[22]，國內最早應用在CZ-2F的逃逸飛行器上增加穩定性[23]。在本項目上，柵格舵的工作馬赫數范圍擴大到高超聲速，并參與控制和機動。不同于美國SpaceX公司的Falcon火箭一子級回收方案，有主發動機和姿控發動機的配合，本項目氣動舵面操縱是姿態穩定和機動的唯一手段(如圖2所示)，因而對氣動特性預測的正確性要求更高，成為飛行成敗的關鍵事項。

圖1 火箭一子級落區控制的柵格舵方案示意圖Fig.1 Illustration of grid fins in the rocket first stage landing area control project

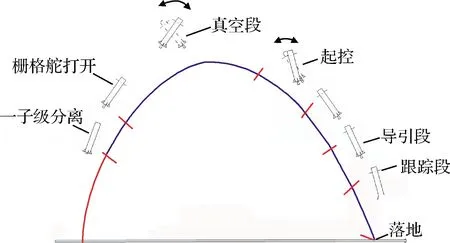
圖2 火箭一子級落區控制飛行流程示意圖Fig.2 Flight process of rocket first stage landing area control

由于柵格舵飛行中操縱狀態較多，跨越馬赫數范圍廣，建立設計氣動數據庫，需要開展規模巨大的風洞試驗和數值仿真工作，對研制經費和進度構成挑戰。為此，本項目團隊探索在氣動數據庫建立上引入基于Kriging模型的機器學習方法，在解決多項技術難題并結合“人在回路”思想后，實現了機器學習方法處理多維復雜工程數據的能力。應用該方法在學習部分風洞試驗及CFD仿真結果基礎上，預測獲得全部工況氣動特性，加快研制進度。2019年7月26日，開展了搭載飛行試驗，人工智能預測氣動特性的方法獲得了飛行驗證。

本文首先簡要介紹了所采用的基于人工智能技術的氣動特性預測方法，然后給出了氣動特性預測結果和飛行試驗驗證情況，最后對人工智能技術與氣動設計進一步深入的結合和應用進行了探討。

1 人工智能氣動特性預測方法

1.1 機器學習算法介紹

針對氣動數據分別來自風洞試驗與CFD計算，具有不同可信度的特點，本文采用了基于加法標度的變可信度(VFM)模型和分層Kriging模型[24]的人工智能預測方法，下面分別介紹。

1)基于加法標度的VFM模型

基于加法標度的VFM模型是一種利用加法標度函數(橋函數)來近似高、低可信度數據修正量的變可信度模型[25-26]，即以低可信度模型為基礎，通過加法標度的方式引入高可信度樣本數據，輔助構建高可信度模型的近似模型。加法標度方法相比于乘法標度方法，能夠使低可信度模型全局地逼近高可信度分析函數，魯棒性更好[26]。

加法標度函數可以表示為：

γ(x)=yhf(x)-ylf(x)

(1)

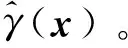
(2)

隨著高可信度樣本點的增多，VFM模型中低可信度數據的影響應逐漸降低，使得最終模型的預估值能收斂到真實函數。

2)分層Kriging模型

韓忠華于2012年提出了分層Kriging模型(Hierarchical Kriging, HK)[24]，它是對傳統Kriging模型理論[26,31]的進一步發展和完善。下面將對HK模型的算法和原理進行簡要介紹。

首先，在帶標簽的低可信度訓練樣本集(Slf,yS,lf)基礎上，建立低可信度的Kriging模型。由于低可信度的樣本相對精度較差，因而可以將這里的標簽認為是“偽標簽”。所建立的低可信度Kriging模型預估值[24]可以表示為：

(3)

其中，

(4)

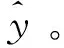
假設在高可信度樣本點處存在靜態隨機過程：

(5)

Cov[Z(x),Z(x′)]=σ2R(x,x′)

(6)

與Kriging模型類似，可推得HK模型的均方誤差為：

(7)

并需滿足如下無偏估計的條件：

(8)

最小化均方誤差(式(7))，即可獲得最優的權重系數w。最終可以推導得到：

(9)

其中，

(10)

則HK模型的預估值可以表示為：

y(x)=β0ylf(x)+rT(x)R-1(yS-β0F)

(11)

其中，

β0=(FTR-1F)-1FTR-1yS

(12)

同時可以得到HK模型預估值的均方差為：

(13)

分層Kriging模型方法將低可信度模型的預估值直接作為全局趨勢函數引入到高可信度模型的建模中，避免了高、低可信度交叉協方差的計算,提供了更合理的模型方差估計,降低了“相關矩陣”的維數，提高了建模效率。

本文首次嘗試將機器學習模型應用于火箭一子級柵格舵復雜氣動特性數據的獲取。在新的應用環境下，場景復雜，對象規律性差。以圖3跨聲速段俯仰力矩特性為例，亞聲速段在0°攻角附近是靜穩定配平點，超聲速變為不穩定配平點，規律復雜。而且飛行姿控設計對俯仰穩定性非常敏感，數據質量要求高。因此，必須改進現有方法，具備良好的魯棒性與泛化能力，才能完成預測任務，下面將一一介紹。

圖3 火箭一子級帶柵格舵外形跨聲速段俯仰力矩特性Fig.3 Pitching moment characteristics of rocket first stage with grid fins in the transonic regime

1.2 機器學習模型相關函數的選擇

Kriging建模過程中R和r的構造均涉及相關函數的選擇和計算。而相關函數只與兩個樣本點之間的歐式距離有關。對于一個m維問題，一種流行的相關函數表示方式為：

(14)

式中:x,x′為兩個不同的樣本點位置；θ=[θ1,…,θm]T∈Rm為待定的模型超參數。

目前常見的相關函數模型有“高斯指數函數”和“三次樣條函數”。“高斯指數函數”的表達式為：

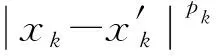
(15)

這里pk代表相關函數光滑程度的各向異性參數[26]。pk=2時，相關函數無窮階次可導。“三次樣條函數”的表達式為：

(16)

其中,ξk=θk|xk-x′k|。該相關函數二階可導，在光滑性和魯棒性方面都表現較好。此外，還有一些基于徑向基函數的相關函數，這類函數無超參數，如薄板樣條函數。

本文選擇了高斯指數函數、三次樣條函數等相關函數，開展了預測對比研究，結果顯示相關函數對預測結果有重要影響。對于氣動設計優化問題，更傾向于選用表現更好的三次樣條函數。而在氣動特性建模預測問題上，兩者的表現正好相反。

圖4提供了采用三次樣條函數預測得到的馬赫數3升降舵引起俯仰力矩特性變化，不同曲線代表不同升降舵舵偏。預測結果發生了不同舵偏曲線交叉的現象，破壞了基本物理特性，預測完全失敗。本文最終選擇了高斯指數函數作為氣動特性預測的相關函數。

圖4 馬赫數3的俯仰力矩預測結果(三次樣條相關函數)Fig.4 AI predicted result of pitching moment coefficient of rocket first stage with Ma = 3.0(cubic spline)

兩者的差異性表現可以給出一個理論解釋。三次樣條函數屬于緊支撐性函數[32]，即當樣本間的距離大到一定程度時，兩者的相關性消失，這點與氣動特性的全局相關性有物理上的沖突。而高斯指數函數，在pk=2時，無窮階次可導，比三次樣條函數更加光滑，可以很好地濾除氣動數據中的噪聲。高斯函數不具備緊支撐性，即使空間樣本點相距甚遠，也依然會考慮兩者的相關性。而火箭一子級的氣動特性預測顯然屬于全局性建模問題，因而采用高斯指數函數可以獲得更好的結果[32]。

1.3 機器學習模型超參數的訓練

在建立Kriging時，可以對模型的超參數θ進行訓練，以提高機器學習的精度和靈活性。

對于分層Kriging模型，由于引入了低可信度樣本，整個樣本點集的似然函數為：

(17)

(18)

其中,n為高可信度樣本點數。將式(18)代入式(17)，兩邊取對數，并去掉常數項后，對數似然函數可寫為：

(19)

此時似然函數僅為超參數θ的函數，但θ并沒有解析解，需要優化算法求解。本文采用的優化算法是結合信賴域方法的Hooke-Jeeves算法。根據以往的經驗，高斯核函數超參數的優化范圍選取區間[10-8θ0, 103θ0]。此外，研究還發現部分工況下固定超參數進行建模預測，有時要比超參數優化后的模型精度更高。

1.4 預測正確性的驗證與確認

如何驗證人工智能預測結果正確性，是應用者最為關心的問題，也是其在工程應用取得成功的關鍵性問題之一。飛行試驗是確認預測正確性的最終極和最可信方式。但這是事后檢驗，對設計者充滿風險，需要更加審慎。工程上更為關心的是在飛行試驗前、數據產生和使用過程中的驗證與確認。

目前，檢驗人工智能預測結果比較流行的方式是采用“交叉驗證”方法，即屏蔽一小部分試驗數據，將其設定為未知，然后用模型預測的數據與之進行比較。這一步對檢驗方法的正確性是必要的，第2.2節提供了對預測方法的交叉驗證結果。但是對工程應用而言，“交叉驗證”還不夠。因為即便在屏蔽點獲得了檢驗，也并不預示其他工況預測的必然正確。因此，還需要進一步的檢驗。

本項目引入了柵格舵氣動特性的物理特性和規律對預測結果進行檢驗。氣動數據并非不可預知的任意數據，它具有普遍性和通用性規律，這為預測的正確性提供了正面影響和保障。這些規律包括：1)數據間的邏輯關系;2)流動物理特征的規律;3)其他來源數據的比對關系;4)類似外形的數據特征。這當中有些規律和關系是強制性的。例如氣動特性的極值應該出現在跨聲速附近和高超聲速條件下的Oswatitsch馬赫數無關原則等。這些規律可以幫助研究人員檢驗數據的正確性。設計階段產生的可靠數據，也可為正確性檢驗提供參考。事實上，該方法也被應用于風洞試驗數據的正確性確認。

1.5 “人在回路”思想

在目前的技術條件下，純粹的數學化計算機智能尚不能滿足工程復雜環境應用的精度和魯棒性要求。一些學者提出了“人在回路”模式，借助人工參與的形式，改進和優化預測結果[33]。文獻[34]中指出：面向工程實際的優化方法需要引入“人機接口”以控制優化進程、引入判斷與創新，其核心在于通過數據管理與可視化以及設計流程的自動化搭建，使設計師能夠便捷地監控優化進程，再根據更新的輸入重建優化進程。類似地，引入“物理學家”監督人工智能預測，在智能運算的前、后進行干預，一個純粹的預測問題成為物理協助下的機器智能問題[35]。“人在回路”的設計流程反映在圖5上。“物理學家”參與的核心是結果的檢驗(見第1.4節)。檢驗結果的反饋將同時作用于參與氣動數據和預測方法上。開發人員有針對性調整參數設置、修正運行等方面的偏差和錯誤，確保在預期條件下運行，獲得滿意的結果。實現這一方法，需要“物理學家”掌握氣動數據的物理規律和預測方法的規律。從某種意義上而言，“人在回路”設計有數據融合的影子。

圖5 基于“人在回路”思想的設計流程Fig.5 Illustration of design process flow based on “man-in-loop” idea

2 柵格舵氣動特性預測和驗證

2.1 訓練樣本集介紹

預測對象是飛行器的六自由度氣動特性，包括三個力和三個力矩。本項目研究中影響氣動特性的要素包括：1)來流條件為馬赫數(0～7)、高度(0～75 km)；2)飛行姿態為攻角、側滑角和滾轉角；3)舵偏狀態為升降舵、副翼、方向舵舵偏角度。

在項目研制初期階段，氣動數據庫的構建以CFD為主。但是由于柵格舵局部結構復雜，網格局部加密的規模巨大，計算效率較低。進入外形凍結階段后，以風洞試驗為主，輔以少量的CFD計算結果作為氣動數據的訓練集。風洞試驗在中國航天氣動研究院1.2 m尺寸的FD-12暫沖式風洞上開展(如圖6所示)。不考慮耦合效應情況下，基本工況需要204個車次，滾轉工況需要816個車次。需要幾個月時間才能完成全部試驗，不能滿足項目緊張的進度要求。此外，高超聲速段氣動特性雖然對再入起控有重要影響，但單次試驗費用較高。綜合考慮進度和成本約束后大幅度壓縮了高馬赫數的試驗工況。表1提供了項目開展的基本工況下俯仰通道的試驗車次情況。根據姿控設計需要，每一馬赫數應該開展-20°～ +20°范圍不同升降舵舵偏的7個車次風洞試驗。亞聲速和跨聲速條件的試驗工況較全，馬赫數4以上狀態未開展試驗。合計僅開展了所需工況的54%。

圖6 火箭一子級帶柵格舵模型在風洞中試驗情況Fig.6 Experimental model of rocket first stage with grid fins installed in the wind tunnel

表1 俯仰特性風洞試驗情況Table1 Fundamental state for wind tunnel experiment on pitching moment characteristics

2.2 預測方法的交叉檢驗

本節給出了預測方法的交叉檢驗結果。以升降舵舵偏操縱引起的俯仰力矩預測作為“交叉驗證”方法算例。高可信度風洞試驗數據分布在7個升降舵舵偏、10個馬赫數和10個攻角的組合工況，共計492組；低可信度CFD計算數據共計96組。從492組高可信度樣本里抽取了25組樣本作為驗證集(馬赫數2的風洞試驗抽取了-5°和-15°兩個舵偏共20組數據，馬赫數3的風洞試驗隨機抽取了5組)，剩余467組高可信度樣本以及全部的低可信度樣本用作模型訓練集。驗證集將被剔除機器學習的學習對象，僅作為檢驗點，檢驗預測結果的正確性。

定義如下指標來校驗模型的預測精度：

1)相關系數r2：

(20)

2)標準均方根誤差eNRMSE：

(21)

3)標準最大絕對誤差eNMAE：

(22)

表2給出了采用交叉驗證方法，模型的預測精度對比。從表2可以看出，相關系數r2非常接近1，均方根誤差eNRMSE與最大絕對誤差eNMAE接近0，表明預測結果具有相當高的精度。圖7給出了預測結果與驗證集的比較，預測結果均通過了未參與訓練的檢驗點。

表2 機器學習方法的交叉檢驗結果Table 2 Cross validation of machine learning prediction method

圖7 升降舵舵偏引起俯仰力矩預測結果的交叉檢驗Fig.7 Comparison of AI predicted result with validation experimental data of pitching moment coefficient caused by elevator deflection

2.3 預測結果

圖8給出了升降舵操縱引起的法向力比較，工況為攻角20°和升降舵舵偏20°。機器學習預測結果通過了試驗點，符合規律。

圖8 升降舵舵偏引起法向力預測與試驗值比較(α=20°)Fig.8 Comparison of AI predicted result with experimental data of normal force coefficient caused by elevator deflection (α=20°)

設計對俯仰力矩特性偏差的容忍度低，預測工作是本項的重點。同時開展了沿攻角和沿馬赫數的雙重檢驗，結果顯示預測結果符合規律。圖9提供了馬赫數2時7個舵偏(-20°,-15°,-10°,-5°,0°,10°,20°)的試驗和預測結果的比較，預測再現了試驗結果。

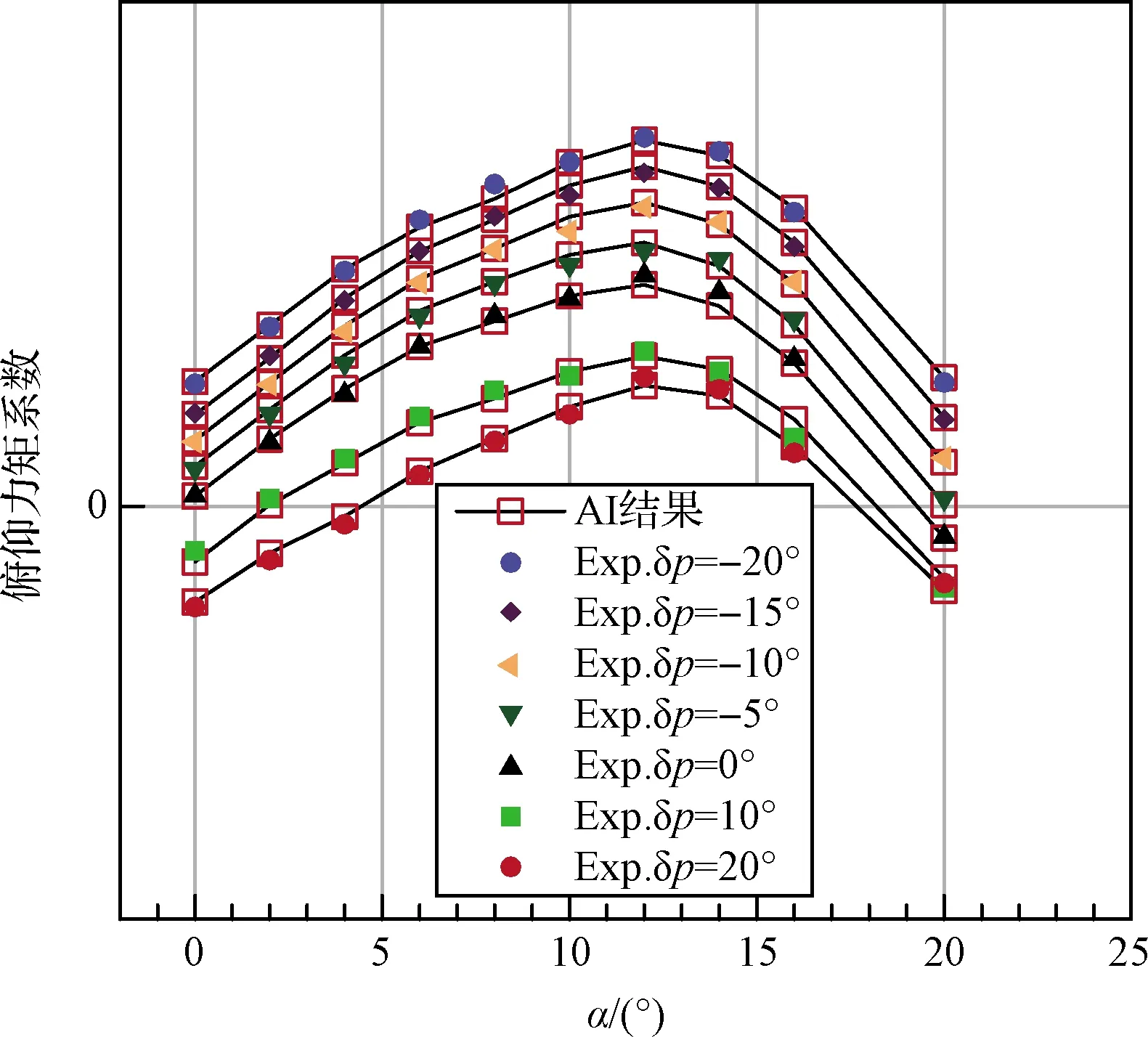
圖9 升降舵舵偏引起俯仰力矩預測與試驗比較(Ma=2.0)Fig.9 Comparison of AI predicted result with experimental data of pitching moment coefficient caused by elevator deflection(Ma=2.0)

圖10提供了馬赫數3.0的俯仰力矩的機器學習結果。在該馬赫數下，僅有0°和-20°舵偏兩個車次的試驗結果。機器學習結果完全重復了試驗結果。其他工況結果符合物理規律。相鄰馬赫數2.0和3.5的試驗結果均顯示攻角20°附近升降舵20°的舵效為零。這一現象可以得到合理解釋，升降舵的合成攻角較大，舵面易發生失速，舵面效率急劇下降。基于氣動特性的常識，介于兩者之間的馬赫數3.0也應該存在這一現象。但是，馬赫數3.0僅有的兩個車次試驗結果無法推導出該現象。不過機器學習預測出舵效為零的現象(見圖10)。這就說明機器學習方法發現了相鄰馬赫數數據的物理規律，并在結果中予以體現。

圖10 升降舵舵偏引起的俯仰力矩預測結果與試驗值比較(Ma=3.0)Fig.10 Comparison of AI predicted result with experimental data of pitching moment coefficient caused by elevator deflection(Ma=3.0)

圖11和圖12展示了機器學習提供的預測結果，其中馬赫數4尚有一個試驗車次，馬赫數5未開展試驗。圖11同時提供了CFD計算結果來進行對比，結果表明預測與CFD結果一致性良好。

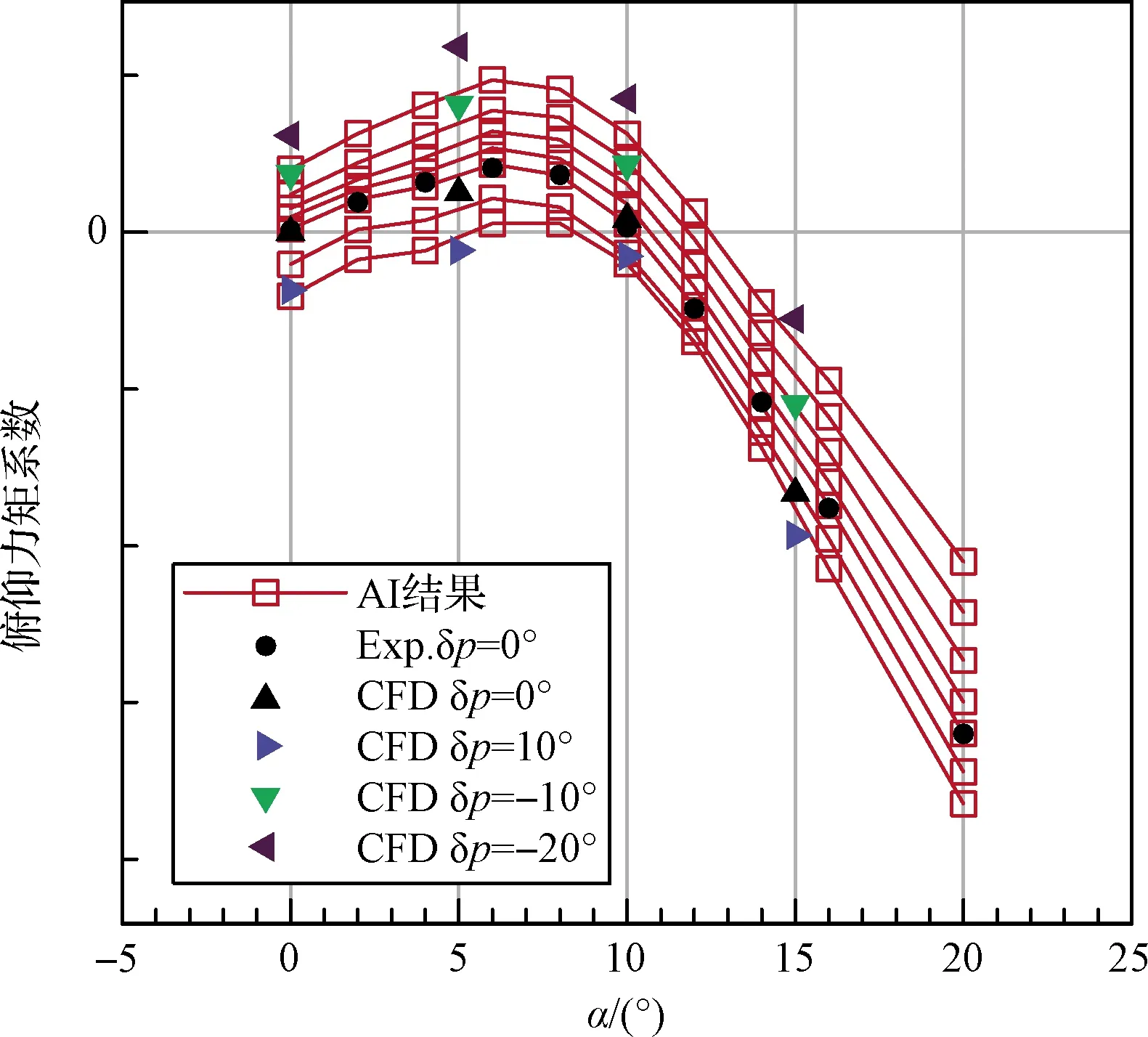
圖11 升降舵舵偏引起的俯仰力矩預測結果與CFD計算結果、風洞試驗值比較(Ma=4.0)Fig.11 Comparison of AI predicted result with CFD and experimental data of pitching moment coefficient caused by elevator deflection(Ma=4.0)

圖12 升降舵舵偏引起的俯仰力矩預測結果(Ma=5.0)Fig.12 AI predicted result of pitching moment coefficient caused by elevator deflection (Ma=5.0)

圖13～圖15給出了5°側滑角引起側向力、偏航力矩和滾轉力矩系數的預測結果比較。為了方便比較，僅提供了攻角為0°的結果,其他攻角的結果也類似。從圖13～15可以看出，人工智能學習的結果與試驗結果趨勢一致,符合物理規律。

圖13 側滑角5°時側向力系數的預測結果與試驗值比較(α=0°)Fig.13 Comparison of AI predicted result with experimental data of lateral force coefficient when sideslip angle is 5°(α=0°)

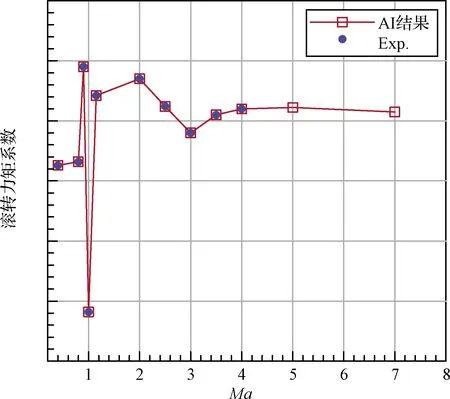
圖14 側滑角5°時滾轉力矩系數的預測結果與試驗值比較(α=0°)Fig.14 Comparison of AI predicted result with experimental data of rolling moment coefficient when sideslip angle is 5°(α=0°)

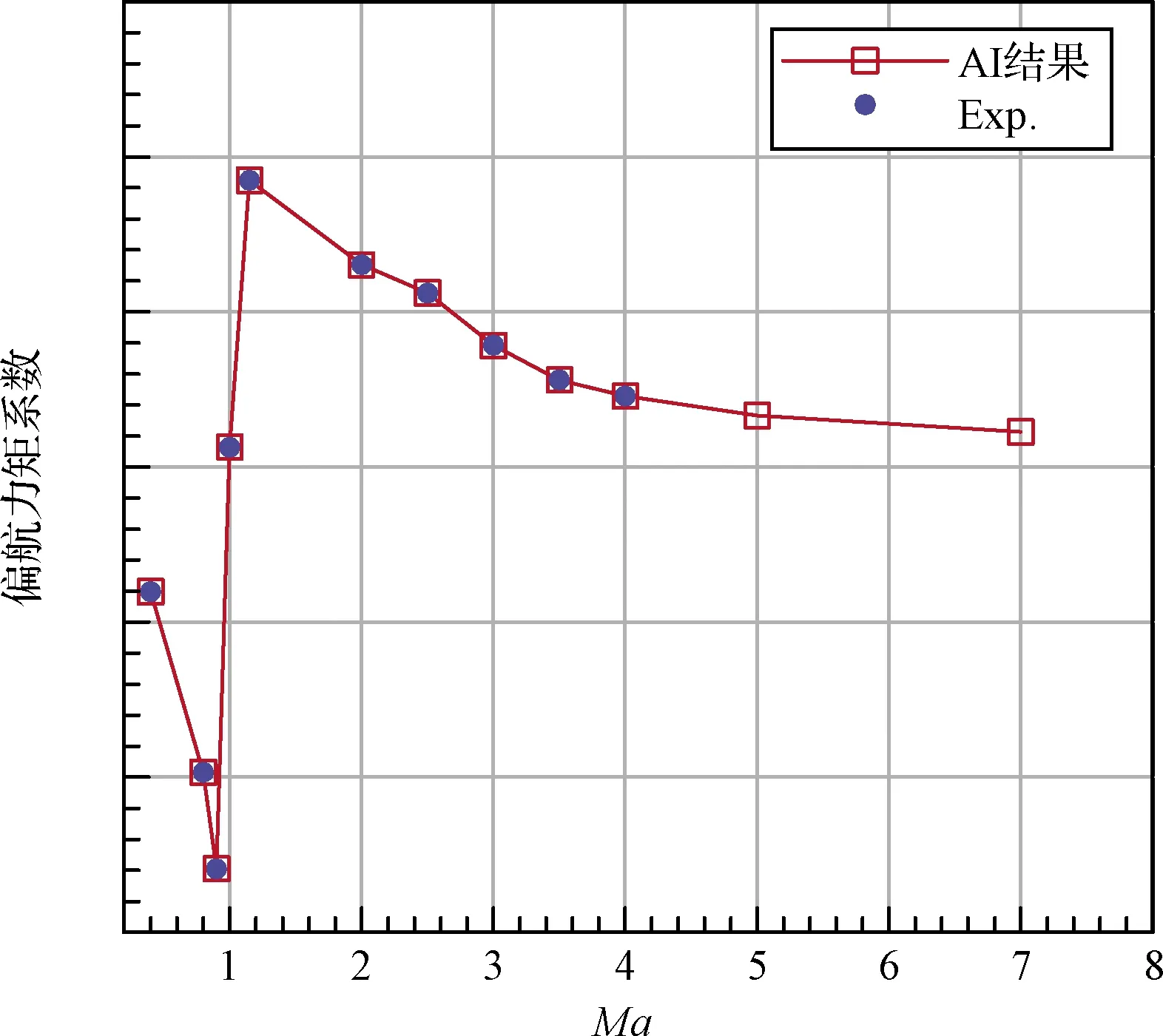
圖15 側滑角5°時偏航力矩系數的預測結果與試驗值比較(α=0°)Fig.15 Comparison of AI predicted result with experimental data of yawing moment coefficient when sideslip angle is 5°(α=0°)

2.4 飛行試驗驗證

2019年7月26日，一子級落區控制項目參加發射搭載試驗，落入預定落區，大幅度縮小落點范圍，取得了成功(見圖16)。箭上四片柵格舵上各自安裝1臺高清攝像頭，對柵格舵在起飛、分離后展開和啟控后工作的全過程進行圖像記錄(見圖17)。圖像顯示飛行全程柵格舵工作情況良好。

圖16 一子級落區控制搭載試驗火箭起飛狀態Fig.16 The take-off state of the test rocket in first stage landing area control project

圖17 高清攝像頭記錄飛行試驗中柵格舵展開的狀態Fig.17 The unfolding state of grid fins in the flight test recorded by HD cameras

圖18和圖19提供了遙測獲取的一子級再入大氣層后的飛行攻角和柵格舵升降舵舵偏歷程。從遙測結果可以看出，一子級殘骸在進入大氣層后，依靠擺動柵格舵的控制能力實現整個子級箭體的穩定和控制。子級再入大氣后的姿態運動特性、柵格舵起控后的運動特性均與設計預測結果相當。跨聲速段俯仰力矩穩定極性變化等多個典型氣動事件均在遙測歷程有所反映。

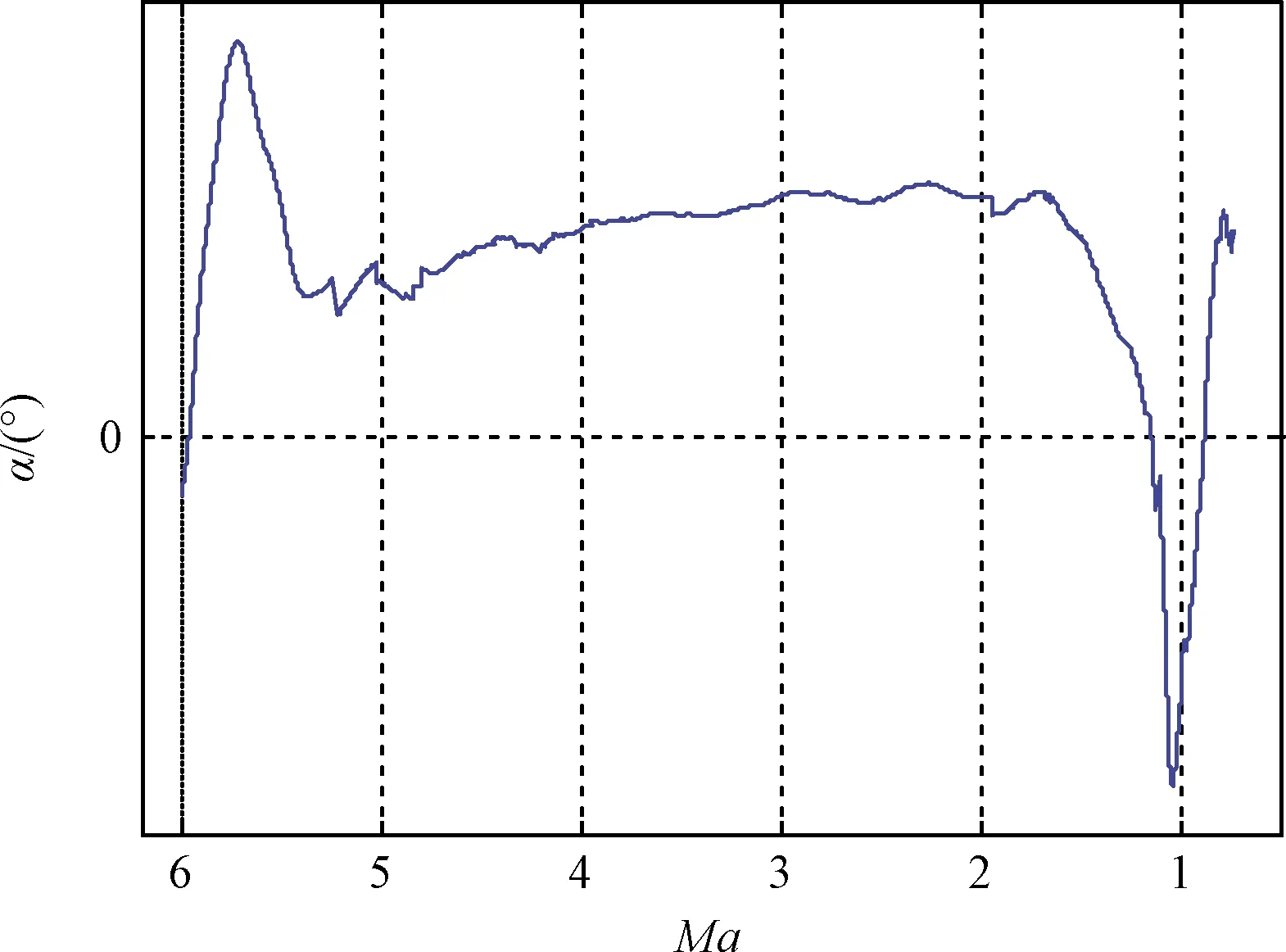
圖18 一子級再入大氣后飛行攻角遙測結果Fig.18 The angle of attack telemetry record for the first satge in reentry flight

圖19 一子級再入大氣后柵格舵升降舵舵偏遙測結果Fig.19 The grid fin elevator deflection angle telemetry record for the first satge in reentry flight

飛行試驗結果表明，通過人工智能方法預測獲得的火箭一子級再入過程寬馬赫數剖面下的氣動特性的正確性和有效性，依靠氣動實現了再入的穩定和可控飛行。

3 人工智能技術在氣動設計應用分級的探討

人工智能預測技術雖然在本項目的應用獲得了飛行驗證，但還是應該清醒認識到該項技術還處于初級階段。未來會有從“低”到“高”的發展過程，智能的內涵和應用結合點也會不斷深化和拓展。

過度拔高無助于人工智能技術的發展。同時，也應該摒棄懷疑和觀望的態度，主動促進融合。技術發展和應用將是一個不斷相互促進的過程。目前需要解決的是，如何增加設計師對智能技術的信任度，解決辦法是對人工智能的技術特征進行劃分和定位，以便于開發人員和應用人員正確理解不同階段人工智能的能力和應用范圍，避免期望過高或是應用錯位。

目前在汽車自動駕駛領域，對自動駕駛技術的劃分提供了一個良好的思路和范例。自動駕駛分為L 0～L 5[36]，依次為無自動駕駛、駕駛員輔助、部分自動駕駛、特定條件下自動駕駛、高度自動駕駛以及完全自動駕駛，既促進了自動駕駛技術的良性發展，也避免了用戶錯誤應用。

為推動人工智能與氣動設計的結合，根據已有的實踐，并參考自動駕駛的分級原則，本文提出人工智能在氣動設計應用的級別劃分。將有助于氣動設計人員正確評估智能技術，建立理性預期，既不提出超越技術階段的目標，也不錯失智能技術提升設計的幫助。應用等級分為A0,A1,A2,A3,A4和A5六個等級。A0是完全無智能技術介入，A5級別最高，可實現完全智能化和自動化。劃分標準和特征見表3。參考分類，可以評估本項目的應用定義為A2級別，具備初級智能，但還需要人工監督。

表3 人工智能技術在氣動設計應用的分級和標準Table 3 Classification and standard of application of artificial intelligence technology in aerodynamic design

4 結 論

在我國首次開展的火箭一子級落區控制項目上，設計團隊發展和應用了基于VFM和分層Kriging模型的氣動特性人工智能預測方法，實現了低成本和快速建立一子級柵格舵外形的氣動特性數據庫，解決了由于進度和經費原因，項目風洞試驗工況不足問題。相關結論如下：

1)本文發展的基于VFM與分層Kriging模型的人工智能的氣動特性預測方法，達到了通過部分風洞試驗結果和CFD結果，去預測完全覆蓋飛行的工況，從而快速和低成本地構建出一子級柵格舵外形氣動特性數據庫，降低設計對風洞試驗的需求。

2)2019年7月26日飛行搭載試驗取得成功，結果表明，本文方法預測的氣動特性結果正確、可靠,說明該方法能夠滿足飛行設計的需求。

3)Kriging模型相關函數選擇和模型超參數訓練對預測結果具有重要影響。采用高斯指數函數的預測效果優于三次樣條函數，這與應用于優化設計的結論有所不同。

4)通過引入“人在回路”技術，成為基于Kriging模型的氣動數據預測的有益補充，降低了數據驅動預測建模風險。

5)結合應用需求，本文提出了人工智能技術在氣動設計應用的分級概念和標準，以推動人工智能技術與氣動設計的融合，為正確理解各階段人工智能的能力和應用范圍提供參考。

后續將繼續探索氣動特性預測與人工智能的深度融合，改進現有基于數據模型的預測方法，發展基于物理的預測準則與方法，進一步提升氣動特性預測的智能化水平。