基于嚴格解析譜的多接收子陣合成孔徑聲吶CZT 算法*

姜 濤 馬夢博 鐘何平

（1.海軍工程大學科研學術處 武漢 430033）（2.海軍工程大學海軍水聲技術研究所 武漢 430033）

1 引言

由于水中聲速較低，廣泛應用于合成孔徑雷達（SAR）領域的“停走停”假設在合成孔徑聲吶（SAS）不再成立［1］，需要建立“非停走停”模型，而實用的SAS 一般采用多接收子陣技術［2］。“非停走停”和收發分置模式導致每一收發陣元對的距離歷程是雙根號之和形式，難以求解點目標響應二維譜解析表達式，從而對使用基于傅里葉變換的快速成像算法帶來不利［3］。

文獻［4］借鑒順軌雙基地SAR精確二維譜的求解方法［5～6］，重新建立了“非停走停”模式下的多接收子陣SAS距離史幾何模型，并對其二維譜進行了精確推導。然而，由于精確的二維譜表達式非常復雜，文獻［4］只將其應用于RD算法，RD算法中距離徙動校正（RCMC）需要用到插值操作，算法效率很低。

本文首先建立了“非停走停”模式下的多接收子陣SAS回波距離史模型，然后給出了點目標的精確二維譜。分析RCM 空變性后發現，RCM 非常接近斜距變量的線性函數，而RCMC是對回波信號包絡的校正，只要校正誤差不超過一個距離分辨單元即可，所以可將復雜的RCM 做一定近似，使其變為斜距變量的線性函數，然后利用Chirp-z變換［7～10］進行RCMC，從而避免了插值運算，提高了算法效率，保證了相位保真度。仿真實驗表明：基于嚴格解析譜的CZT 算法成像精度在近距離處優于基于DPC近似［11］的CZT算法。

2 多接收子陣SAS回波信號

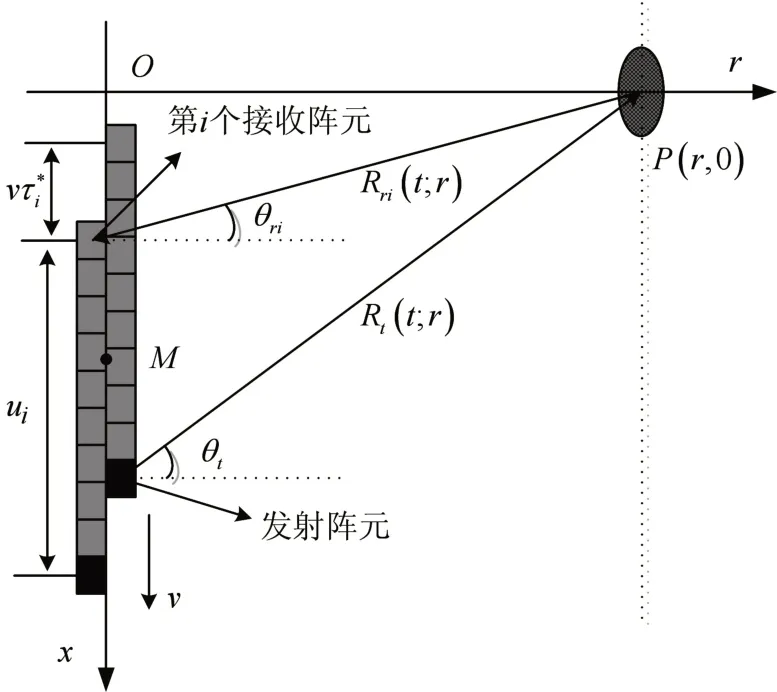
圖1 多接收子陣SAS幾何模型

多接收子陣SAS 幾何模型如圖1 所示，坐標軸定義如下，r軸表示距離向（斜距），x軸表示方位向，平臺沿方位向以速度ν勻速直線運動。假設海底為理想平面，任意點目標為P(r，0 )，在“非停走停”模式下，發射陣元（黑色方塊）以頻率PRF 發射脈沖信號，脈沖信號經點目標反射后被N個接收陣元（灰色方塊）接收，M點表示發射陣元與第i個接收陣元的中點，θt和θri分別表示發射時刻和第i個接收陣元接收時刻的斜視角。ui表示發射陣元與第i個接收陣元的距離，表示脈沖發射到被第i個接收陣元接收這段時間內平臺移動的距離。x=νt表示t時刻M點的位置，則發射陣元、第i個接收陣元與點目標的距離可分別表示為

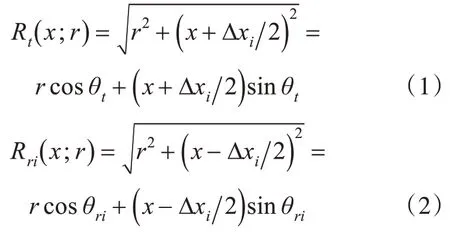
則第i個接收陣元距離史為

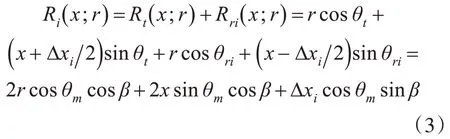
假設發射信號為線性調頻脈沖信號，則第i個接收陣元接收到的回波信號基帶形式可以表示為

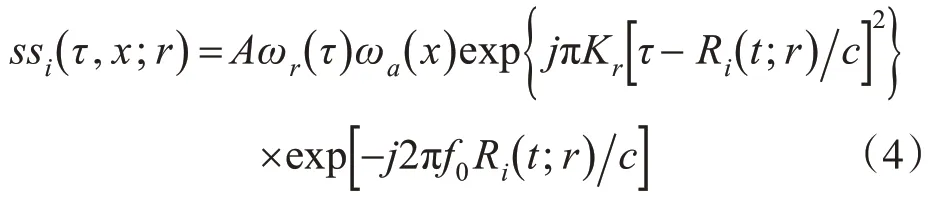
其中f0表示發射脈沖信號中心頻率，Kr表示發射脈沖信號的調頻斜率，ωr(τ)表示發射脈沖信號包絡，ωa(t)表示方位向天線方向圖，A表示幅度項，如無特別說明，后文公式推導忽略與成像質量無關的幅度項。

3 基于嚴格解析譜的CZT算法

3.1 波數域點目標響應二維譜

對式（4）進行二維FFT可得

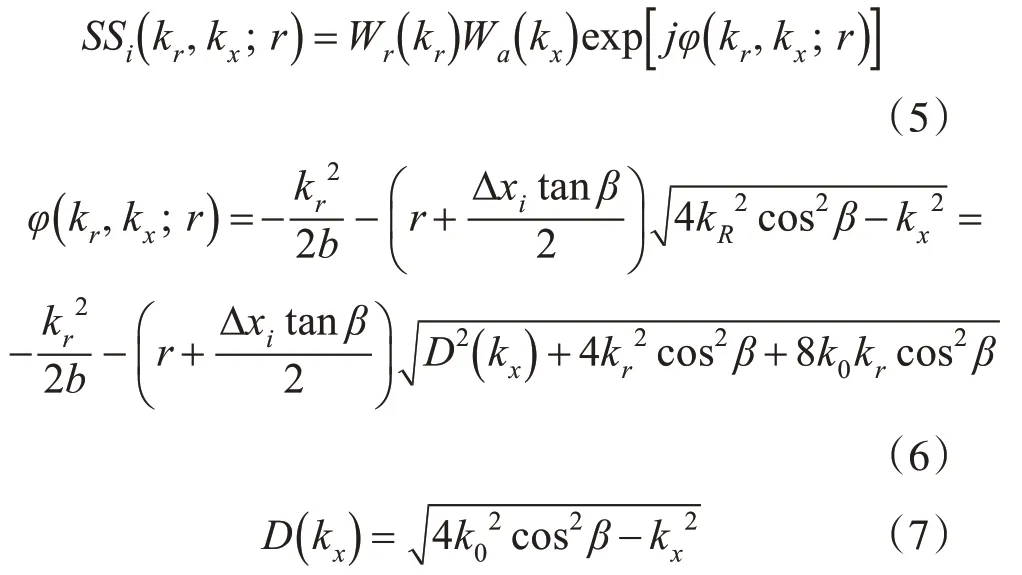
其中Wr( · )表示發射信號頻譜包絡，fr為距離向基帶頻率，表示方位向波數，fa為方位向向多普勒頻率，表示距離向中心波數，表示距離向基帶波數，kR=k0+kr表示距離向波數。

根據文獻［4，12］可得半雙基角近似表達式為

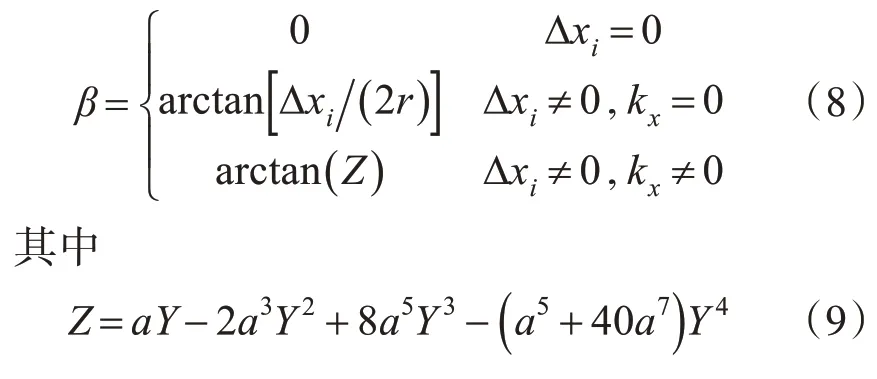
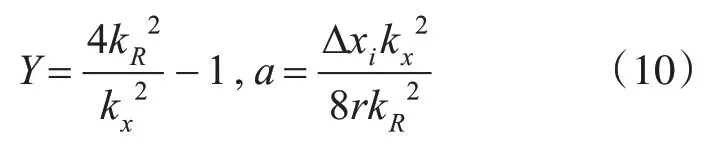
由于半雙基角β一般很小，在窄帶條件下，可以近似認為β與距離向基帶波數kr無關，即

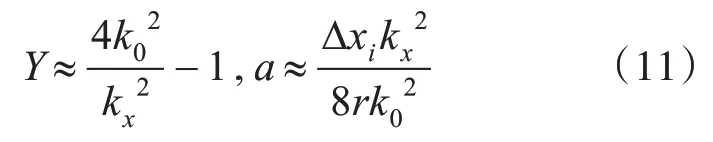
將式（6）中的根式展開成kr的冪級數，保留至項，則

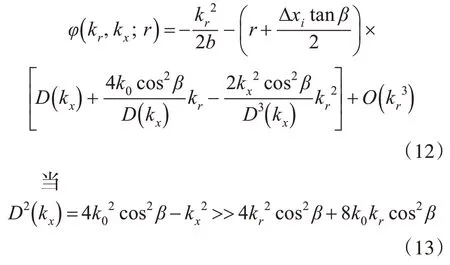
時，式（12）中的高次項可忽略。

由于多接收陣SAS一般工作在正側視模式，且半雙基角β一般很小，所以條件（13）成立。忽略式（12）中高次項，并進行整理的到

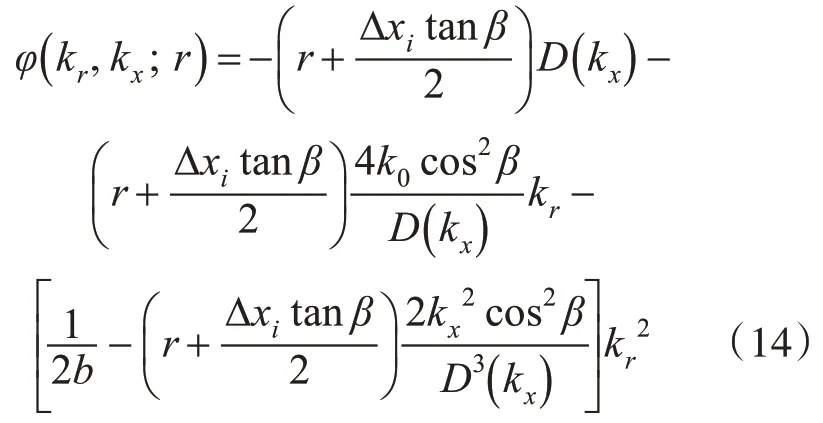
式（14）中第一項為方位調制項，第二項為距離徙動項，第三項為距離壓縮項與二次距離壓縮項。由于距離徙動項是距離變量r的非線性函數，從而無法直接運用Chirp-z 變換進行距離徙動校正，所以必須首先對距離徙動項進行線性化處理。

3.2 距離單元徙動空變性分析

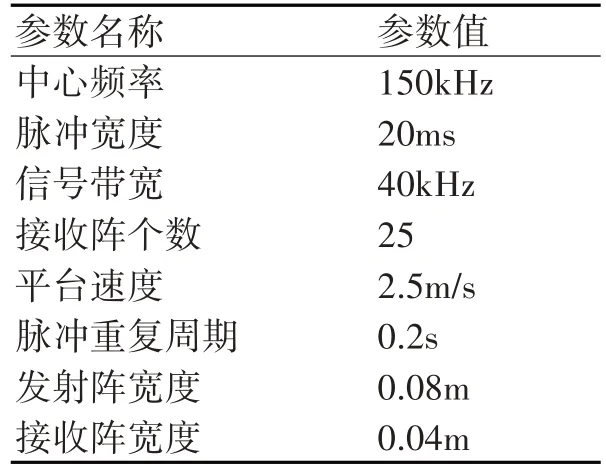
表1 仿真參數

記精確距離單元徙動為

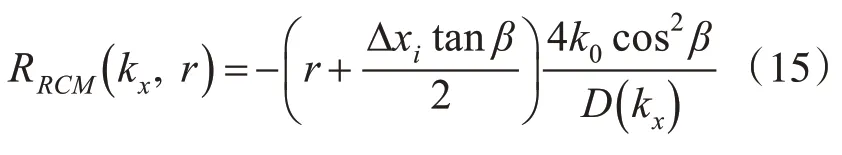
式（15）中RRCM(kx，r)是方位向波數kx和距離變量r的函數，設聲吶參數如表1 所示，距離單元徙動RRCM(kx，r)隨r和kx變化如圖2（a）所示，陣元間距取最大值ui=1m。

由于β和D(kx)與距離變量r弱相關，且Δxi＜＜r，為使RRCM(kx，r)變為距離變量r的線性函數，不妨設近似距離單元徙動

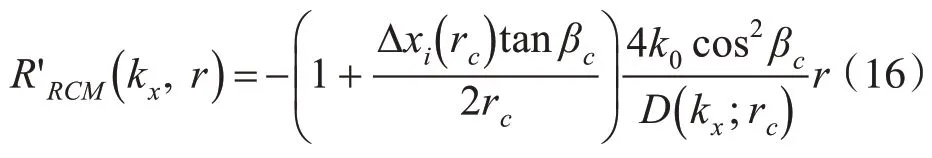
其中rc表示參考距離，βc表示參考距離處的半雙基角，則 距 離 單 元 徙 動隨r和kx變化如圖2（b）所示。

定義式（15）與式（16）的近似誤差為ΔR，即

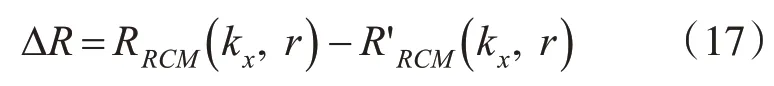
近似誤差 ΔR隨r和kx變化如圖2（c）所示。

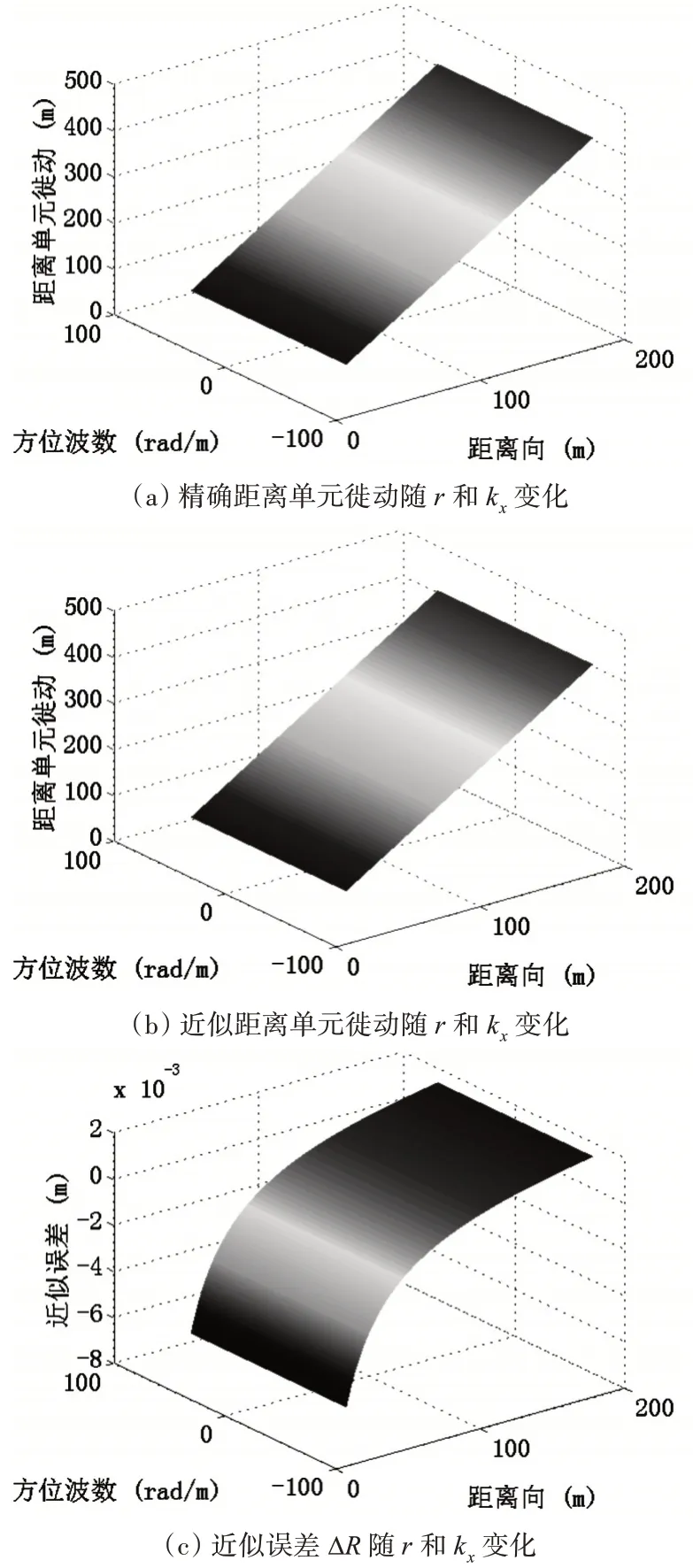
圖2 精確距離徙動與近似距離徙動比較

對比圖2（a）與圖2（b）可以發現，線性處理后的距離單元徙動與原始距離單元徙動RRCM(kx，r)變化規律幾乎一樣，兩者的差值，即近似誤差 ΔR反應在圖 2（c）中，從圖 2（c）中可以看出，近似誤差 ΔR遠小于一個距離分辨單元0.0187m，用線性處理后的距離單元徙動進行距離徙動校正可滿足成像要求。

3.3 基于嚴格解析譜的CZT算法流程

對于每一個接收陣元而言，方位向都是欠采樣的，但可以采用方位譜擴展方法，沿方位向對每個接收陣元的二維譜進行擴展。然后再利用傳統的收發合置CZT算法進行成像處理。具體步驟如下。

步驟1距離壓縮和SRC。該操作通常在二維頻域進行，但是由于該域不能同時表征距離和距離頻率，因此一般通過與一個參考距離處的參考相位相乘予以消除，參考因子為

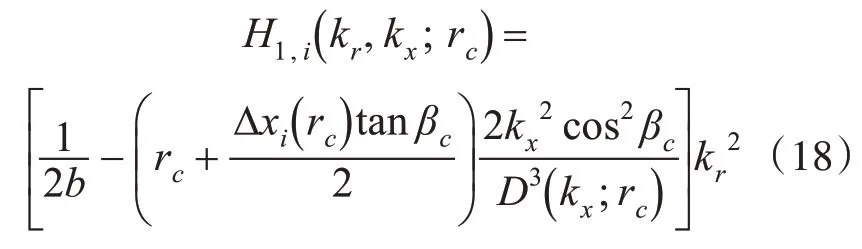
步驟2利用Chirp-z 變換校正RCM。首先以參考距離對RCM進行一致補償，參考因子為

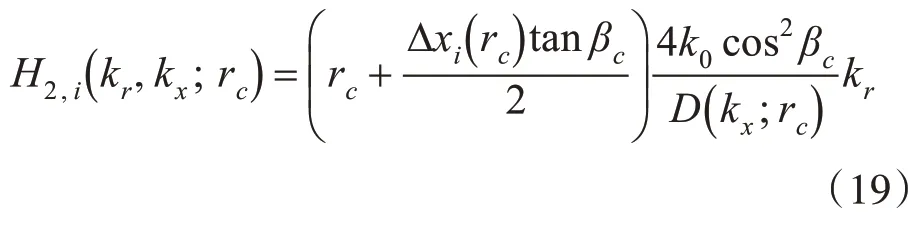
這一操作可以與步驟1 一起進行。此時二維譜可表示為

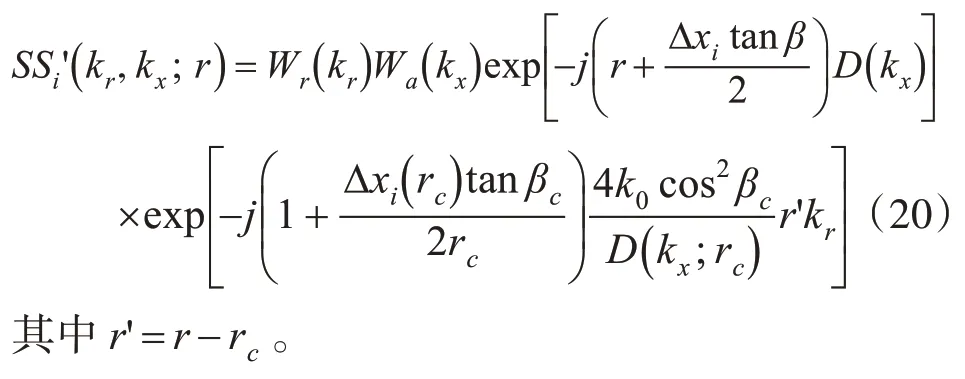
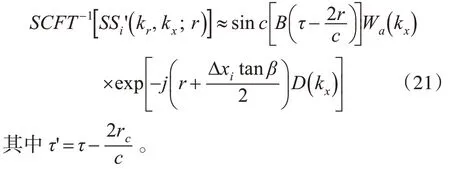
則式（21）可以寫成

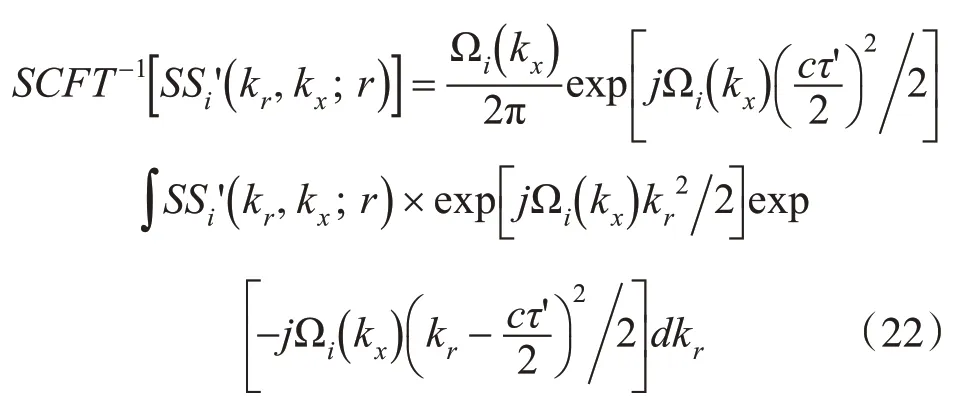
式（22）表明Chirp-z變換可以通過兩次相位乘和一次卷積完成，即二維譜先與進行復乘，然后與進 行 卷 積 ， 最 后 與復乘。其中卷積操作可通過FFT快速實現。

步驟3方位壓縮和剩余相位校正。該操作通常在RCMC之后于RD域通過與一個距離空變的參考相位相乘予以校正，參考因子為

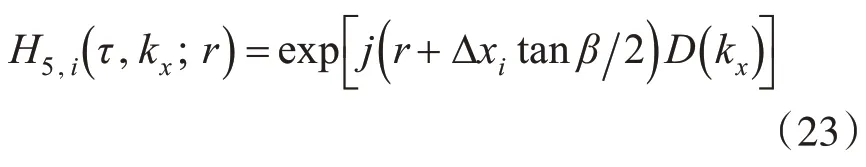
此時距離多普勒域信號可表示為

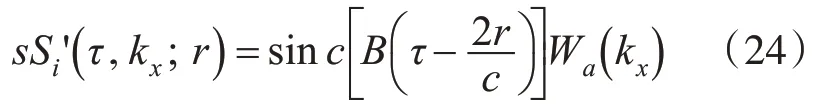
步驟4數據融合與方位IFFT。對所有接收陣元回波信號完成上述操作后，將其進行疊加，即

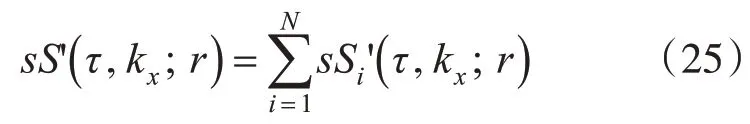
數據融合之后，經過方位向IFFT 回到二維時域即可獲得重建的SAS圖像。具體流程如圖3 所示。

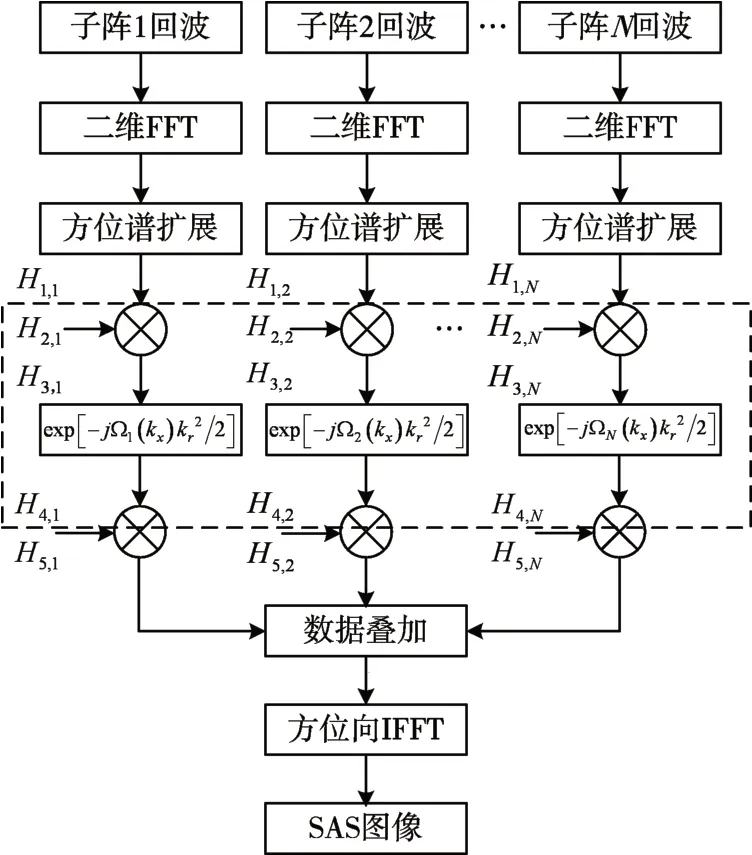
圖3 基于嚴格解析譜的CZT算法流程圖

4 仿真實驗

為驗證本文算法的正確性，下面對不同距離點目標進行仿真，仿真參數如表1 所示。在場景中的近距離和遠距離處分別設置一個點目標，坐標分別為(4 0，10 )和 (1 30，10 )。分別采用基于DPC 近似的CZT 算法和基于嚴格解析譜的CZT 算法進行成像處理，成像處理過程中方位向和距離向均不加任何窗函數，對于近距離點目標的成像結果如圖4 所示。

從圖4 中可以看出，對于近距離點目標，采用基于DPC 近似的CZT 算法和基于嚴格解析譜的CZT 算法得到的圖像在方位分辨率上沒有明顯差別，但采用基于DPC近似的CZT算法得到的圖像的旁瓣明顯高于采用基于嚴格解析譜的CZT 算法得到的圖像的旁瓣。

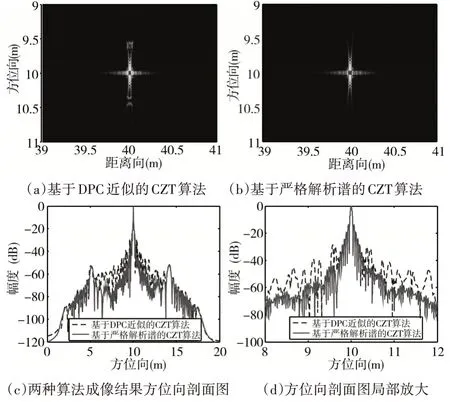
圖4 近距離點目標成像結果

對于遠距離點目標，成像結果如圖5 所示。

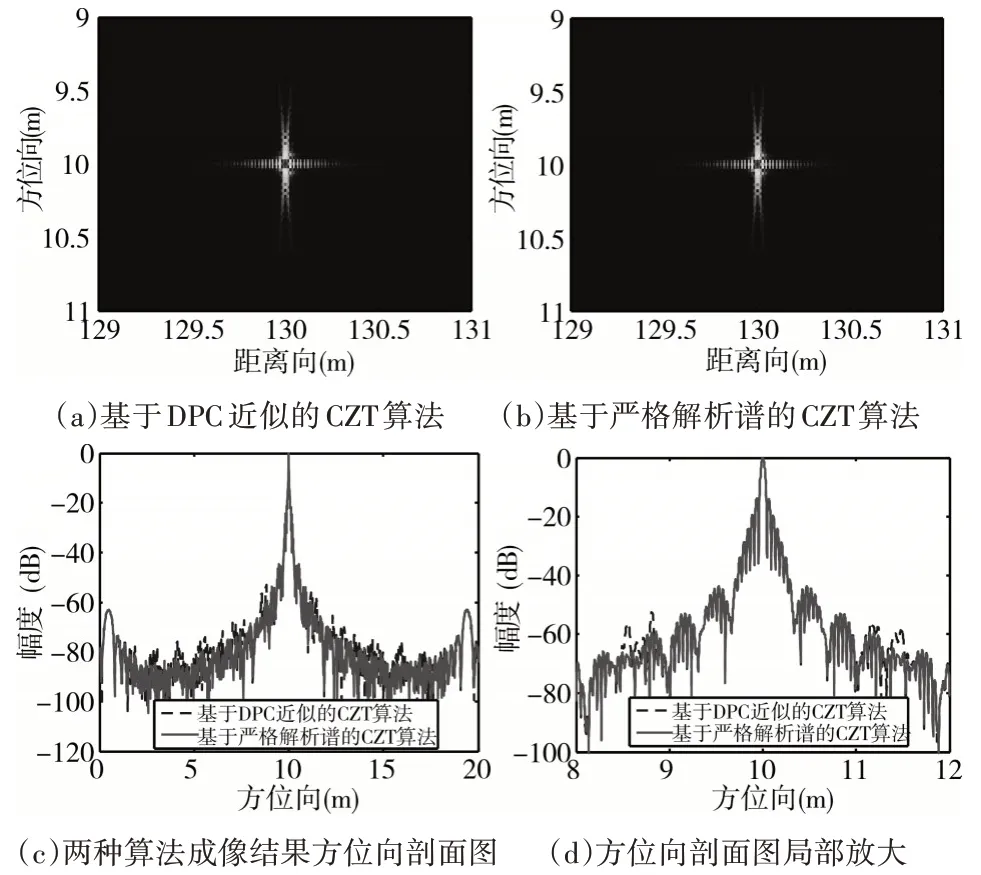
圖5 遠距離點目標成像結果

從圖5 中可以看出，對于遠距離點目標，采用基于DPC 近似的CZT 算法和基于嚴格解析譜的CZT 算法得到的圖像在方位分辨率上沒有明顯差別，但采用基于DPC近似的CZT算法得到的圖像的旁瓣還是略高于采用基于嚴格解析譜的CZT 算法得到的圖像的旁瓣。

綜合以上兩種情況不難發現，基于嚴格解析譜的CZT算法在方位分辨率方面沒有明顯優勢，其主要優勢體現在旁瓣上，尤其是在近距離處，這是由于DPC近似在近距離處誤差較大導致，而采用嚴格解析譜的方法則可以避免這種誤差。

5 結語

本文基于的嚴格解析譜，將其RCM 近似為斜距變量的線性函數，然后利用Chirp-z 變化校正距離徙動，進而提出基于嚴格解析譜的多接收子陣SAS CZT 算法，最后通過仿真實驗驗證了本文算法相對于基于DPC近似的CZT算法更加精確。