基于Matlab的加工鉆頭螺旋槽砂輪截形的干涉誤差分析

贠 良，董黎敏，王澤巍，王 瑞，董 良

（1．天津理工大學 機械工程學院 天津市先進機電系統(tǒng)設計與智能控制重點實驗室，天津300384；2．天津市宏維刀具有限公司，天津300110）

標準砂輪在工件成型中應用廣泛，選定標準砂輪進行螺旋槽成型加工時雖然可以磨削出滿足常規(guī)參數的螺旋槽，但是有些特定鉆頭螺旋槽無法用標準砂輪精確磨削，需要根據已知的螺旋槽進行非標砂輪的設計.在砂輪反求設計中，通常需確定端截形的擺放位置，砂輪與螺旋槽的相對位置，而反求中，砂輪位置的不確定性和其他因素，必然導致反求誤差[1-2].干涉誤差分析就是對反求得到的砂輪回轉體與當時螺旋面的位置關系進行定量分析，從而準確的判斷砂輪位置參數設置的合理性，間接預測出所求砂輪磨削出的螺旋槽與已知螺旋槽的差異程度[3-4].

本文首先建立了加工螺旋槽的砂輪數學模型，為砂輪截形的反求提供了理論基礎，在此模型的基礎上對砂輪位置參數進行干涉誤差分析判斷，提出了計算干涉誤差ΔR的數學模型，基于所求砂輪截形上相應點對干涉誤差值數組ΔR進行了計算.然后在砂輪的計算實例中，用Matlab編制截形繪制程序和數組ΔR的計算程序，運行程序得到砂輪截形離散圖、擬合圖以及ΔR數組.最后根據得到的數組ΔR，可以了解砂輪截形上相應點對應截面的干涉值，并求出最大干涉值.改變砂輪位置參數值，觀察所求砂輪截形和最大干涉值的變化.

1 加工螺旋槽的砂輪數學模型

1.1 坐標系的建立及坐標變換

按照磨削加工時鉆頭、砂輪和機床的相對位置關系建立坐標系（如圖1所示）.在機床上建立坐標系O3-x3y3z3，在砂輪上建立坐標系O1-x1y1z1，以上兩坐標系固定，位置關系由O1點在機床坐標系O3-x3y3z3上的坐標（a，b，c）和砂輪軸z1與鉆頭軸線的夾角λ確定.在鉆頭上建立坐標系O2-x2y2z2.砂輪坐標系先繞x1軸旋轉λ角，然后平移（a，b，c），得到機床坐標系.由此可反求得到機床坐標系到砂輪坐標系的轉換式為

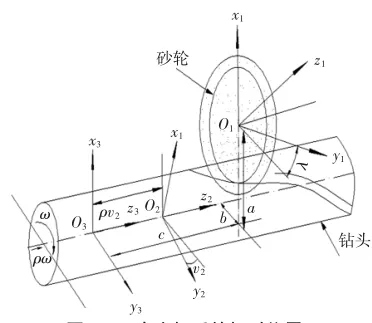
圖1三個坐標系的相對位置Fig.1 Relative position of three coordinate systems

1.2 鉆頭螺旋面數學模型

鉆頭坐標系O2-x2y2z2起始位置與機床坐標系O3-x3y3z3重合，此時在O2-x2y2平面上建立的端截形，隨著鉆頭坐標系或鉆頭做螺旋運動，即繞鉆頭軸線旋轉同時沿其軸向移動，便可得到機床坐標系下的螺旋曲面.則在初始O2-x2y2平面上擺放端截形的位置不同決定了螺旋槽擺放位置的不同，其擺放位置對應的不同方程可以由兩個坐標的旋轉變換實現，如圖2所示.

端截形的方程式為

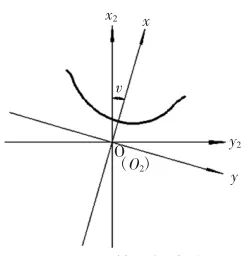
圖2旋轉坐標變換Fig.2 Rotation coordinate transformation

式中u2為參變數.

由式（2）可以得到螺旋曲面的方程[5]

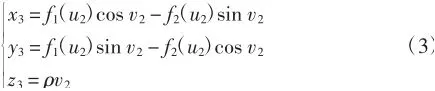
式中v2為角度參數，表示端截形從開始位置繞z3軸轉過的角度.順著z3軸看，以順時針方向轉動為正；ρ為螺旋參數，ρ=導程T/2π，表示端截形繞著z3軸轉過單位角度時，沿z3軸線方向移動的距離.

1.3 砂輪回轉表面數學模型

在砂輪坐標系O1-x1y1z1上，砂輪回轉表面可以由平面O1-x1z1上的母線繞z1軸旋轉得到.砂輪軸向截形的方程式表示為

式中，u1為參變數.由式（4）可以得到砂輪坐標系下的砂輪回轉表面方程式[6]

式中，v1為角度參數，表示砂輪軸向截形所在的平面繞砂輪軸線旋轉的角度.

由砂輪回轉曲面方程式（5）得到砂輪坐標系下垂直于砂輪軸線的截面方程，表示為

把螺旋面方程式（3）代入機床坐標系到砂輪坐標系的轉換式（1）中得到砂輪坐標系下的螺旋面方程式.

2 干涉誤差分析

2.1 干涉分析理論

由上述砂輪截形的反求理論可知，在端截形擺放位置和砂輪與螺旋槽相對位置確定的前提下，便可反求出砂輪截形，干涉誤差分析就是對反求得到的砂輪回轉體與當時螺旋面的位置關系進行判斷[7].

為說明干涉分析，假想將求出的砂輪實體模型和已知的螺旋槽，按照反求砂輪時端截形擺放位置和砂輪與螺旋槽的相對位置放置，用垂直于砂輪軸線的平面所截砂輪和螺旋槽，判斷平面所截砂輪形成的圓端面與平面所截螺旋槽形成的端截面是否有交集.若在砂輪厚度范圍內所有垂直于砂輪軸線所截的兩個端截面存在交集即為干涉，若所有平面所截的兩個端截面不存在交集即為不干涉.

由剖平面所截砂輪得到截圓，所截螺旋槽得到一截面，如圖3所示.通過剖截面所截螺旋槽形成的截面外表曲線上的點到截圓中心的距離，與在此剖面下截圓的半徑求差來定量分析干涉誤差.如圖4所示，A點為外表曲線上任意一點，L為A到圓心O的距離，圓的半徑為R，ΔR=L-R，若ΔR大于等于零，說明A點在圓的外面及邊緣，不干涉；反之，ΔR小于零，說明A點在圓的內部，說明所求的砂輪會干涉螺旋槽，此時的ΔR值表明了干涉程度.

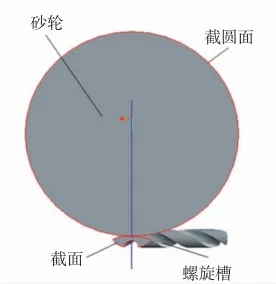
圖3螺旋槽和砂輪剖面圖Fig.3 Sectional view of spiral groove and grinding wheel

本文是在垂直于砂輪軸線的剖面中研究的，所以需要求出螺旋槽在此剖面的方程式.根據在同一剖面內砂輪回轉曲面和螺旋面的z1相等，由（6）和（7）得到等式

圖4圓與外表曲線的位置關系Fig.4 Positional relationship between circle and outer surface curve

根據式（8），給定一個g2（u1）=Z1，即選定一截面，若給定一個u2，便會得到對應的一個v2.其含義是在確定一垂直于砂輪軸線的剖面上，選取之前代表端截形上的點，通過式（8）求解出端截形上的點，成為與此點共螺旋線的所截螺旋面剖面上外表曲線上的點時旋轉的角度.將代表端截形點的u2與求出的v2代入到式（7）中，得到砂輪坐標系下與端截形上各點共螺旋線的剖面上外表曲線上點的坐標.在定剖面內，由外表曲線上點的坐標得到此點距所截砂輪形成圓中心的距離，然后與圓的半徑相減，得到ΔR的表達式如下.

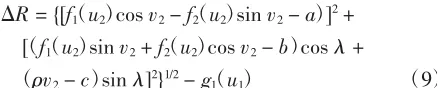
2.2 基于所求砂輪截形上相應點的干涉分析判斷

基于砂輪截形上的相應點來判斷干涉情況，每取一個所求砂輪截形上的相應點，即得到一個點坐標（x1，z1），其中z1對應于一個z1剖平面，x1表示z1平面所截砂輪形成截圓圓半徑.將z1=g2（u1）代入（8）中，得到一個關于u2與v2的等式，根據等式由端截形上的m個u2分別得到相應的m個v2.將這m組u2，v2和x1=g1（u1）代入式（9）中，得到z1剖面下m個ΔR.由m個砂輪截形上的相應點，得到m×m個ΔR.判斷這m×m個ΔR值，若存在負數，就說明存在干涉.負數的大小確定了干涉程度.同樣干涉分析的精確度也和反求時端截形上取點量有關.

3 基于Matlab的砂輪截形干涉誤差分析求解實例

以半徑R=5.347 mm，半芯厚r=1.266 mm，α=30°（鉆頭螺旋角）的硬質合金鉆頭為例，編制Matlab計算程序[8].首先定義用到的常量和變量，然后通過數組之間的運算來實現接觸點的運算和坐標變換；最后通過Plot命令繪制砂輪軸向截形的散點圖及擬合圖，再通過所求砂輪截形上的相應點得到關于ΔR的數組.通過對ΔR數組中的每行元素尋找最小值，若最小值大于等于零，說明這行對應的截面不發(fā)生干涉，記為零；若最小值小于零，即發(fā)生干涉，記為最小值，也為這個截面的最大干涉；得到一個一維數組，再尋找最小值，便會得到整個ΔR數組中的最小值，即最大干涉誤差.

3.1 基于Matlab的砂輪軸向截形的繪制

圖5砂輪軸向截形Fig.5 Axial section of grinding wheel

由鉆頭端截形反求砂輪截形時，為簡化計算，將端截形型線劃分為四段圓弧：圓弧AB為倒角1，大圓弧段BC，小圓弧段CD，圓弧DE為倒角2，如圖5所示.每段圓弧對應的方程式和圓心角都不同，求得的砂輪軸向截形也不同，故而在Matlab中使用linspace命令，采用ployfit函數進行曲線擬合，分別在每段圓弧的圓心角范圍內均分得到10個u2，很顯然端截形由40個點代替進行計算.如圖6所示.

圖6砂輪軸向截形上的40個相應點的散點圖及擬合圖Fig.6 Scatter diagram and fitting diagram of 40corresponding points on axial section of grinding wheel

本文以a=80 mm，λ=60°的砂輪截形繪制程序為例，求得砂輪軸向截形上相應點的坐標數組W3，也就是得到了砂輪截形上的40個相應點坐標，見表1.

3.2 所求砂輪截形上相應點的ΔR數組計算程序

由數組W3可知其中有3個坐標值相同，去除掉相同點得到數組W4，即求出輪截形上的37個相應點，同時對應于倒角1圓弧上對應10個離散點，大圓弧上對應9個離散點，小圓弧上對應9個離散點，倒角2圓弧上對應9個離散點.由于端截形由四段圓弧組成，所以求解ΔR數組時，仍需要每段圓弧分別求解最后整合.針對倒角1對應圓弧的ΔR數組DDD求解，由所求砂輪截形上37個相應點集的z1坐標，得到砂輪厚度范圍內的垂直于砂輪軸線的37個截面，每取一個截面，就需要求出與此段圓弧10個離散點共螺旋線的此截面所截螺旋面外表線上的10個相應點對應的ΔR，從而求出此段圓弧37個截面對應的ΔR數組DDD，其計算程序如圖7所示.

表1 a=80 mm，λ=60°時反求得到砂輪截形上40個相應點的坐標Tab.1 a=80 mm andλ=60，the coordinates of 40 corresponding points on the grinding wheel section are obtained by reverse calculation

圖7倒角1圓弧對應的ΔR數組計算程序Fig.7ΔR array calculation program corresponding to chamfer 1 arc

由以上程序同理可得到大圓弧段、小圓弧段和倒角2所對圓弧對應的ΔR數組DDD1，DDD2和DDD3，最后合并四個數組得到總的ΔR數組P（37，37）.數組P中37行代表37個截面，每行的37列元素代表此截面所截螺旋槽外表線上的37個點的ΔR值.

求出的ΔR數組P（37，37）有1 369個元素，通過判斷每個元素的大小尋找到每行數據對應的最小值，判斷最小值的正負，若ΔRmin≥0，說明此行元素都大于等于0，肯定不會有干涉，用0來表示此行不干涉；若ΔRmin＜0，說明此截面會發(fā)生干涉同時最小值也是最大干涉程度，用最小值來表示此行干涉和干涉程度.最終得到數組H（1，37），經過在數組H中尋找最小值得到最大干涉值MAX.數組P的元素搜尋流程圖如圖8所示.

圖8數組P的元素搜尋流程圖Fig.8 Element searching flow chart of array P

同樣以a=80 mm，λ=60°的砂輪截形反求為例，運行以上程序，可以得到數組H.

H=[-2.06e-15，-1.2e-14，0，0，-1.06e-14，-4.8e-15，0，-3.18e-15，-5.09e-15，0，-1.05e-15，0，0，-4.34e-15，-3.92e-15，-1.45e-14，-3.68e-15，0，0，0，0，0，-5.33e-16，0，-7.41e-16，0，-5.40e-15，0，0，0，0，0，0，0，0，0，0]，MAX=-1.45e-14

由得到的數組H，可以發(fā)現反求砂輪截形上37個相應點對應的37個截面上有14個截面會產生干涉誤差，其誤差值大約都在-e-14或-e-15左右，誤差值極小，間接地說明所求砂輪磨削出的螺旋槽與已知螺旋槽差異極小.同時由MAX值，可以得到最大干涉值，可以說明：干涉誤差小于-1.45e-14 mm（高精度數控刀具干涉誤差應小于-1.5e-10 mm），砂輪位置參數的選取是合理的，由此反求的砂輪是可以加工出已知的螺旋槽的[9-10].

3.3 改變參數的砂輪截形和MAX值

1λ=60°時，a改變，砂輪截形和MAX值的變化

編制完以上程序后，根據一般砂輪直徑大小，分別取a=40、50、60、70、80、90（單位為mm），通過更改a的大小得到不同的M文件，運行程序可以得到相應的砂輪截形和MAX值，并將其圖形放置于同一坐標系進行比較，可以發(fā)現砂輪直徑的變化對截形的變化影響較小，最大干涉值變化也不太明顯.a變化對截形的影響如圖9、10所示.

圖9λ=60°a變化時，砂輪截形和最大干涉值Fig.9 Whenλ=60 a changes，the grinding wheel profile and maximum interference value

圖10λ=60°，a變化時，所求砂輪截形和最大干涉值及比較Fig.10λ=60，when a changes，the profile of grinding wheel and the maximum interference value are obtained and compared

2a=80 mm，λ改變，砂輪截形和MAX值的變化

a取80 mm時，λ在60°附近取值，觀察砂輪截形和MAX值的變化.λ分別取57°、58°、59°、60°、61°、62°，λ變化的砂輪截形和最大干涉值變化如圖11所示.

由圖11可以發(fā)現，在λ=57°、58°、59°、60°、61°時最大干涉值在-e-14或-e-15范圍內，取λ=62°時截形直接出現畸形.

圖11 a=80mm，λ變化時，砂輪截形和最大干涉值Fig.11 a=80 mm，whenλchanges，grinding wheel profile and maximum interference value

4 結論

由非標整體硬質合金鉆頭，通過分析砂輪和螺旋槽的基本嚙合條件，建立了砂輪坐標系下砂輪截圓和鉆頭端截形的數學模型.通過剖截面所截螺旋槽形成的截面外表曲線上的點到截圓中心的距離，與在此剖面下截圓的半徑求差來定量分析干涉誤差，提出了干涉誤差數組ΔR的計算方法.在實例計算中，使用Matlab軟件編制了繪制砂輪截形和計算數組ΔR的程序.運行程序得到砂輪的軸向截形以及ΔR數組.由ΔR數組得到了最大干涉誤差值為-1.45e-14 mm.根據高精度數控刀具干涉誤差應小于-1.5e-10 mm，故砂輪位置的選取是合理的.進行干涉誤差數組ΔR的計算，能定量地研究砂輪位置參數選取的合理性，同時也為砂輪反求時位置的確定提供了一定的支持.