斜拉橋斜拉索有限元模擬方法的比較

錢淼 朱運(yùn)河 何東升

（中鐵大橋勘測(cè)設(shè)計(jì)院集團(tuán)有限公司，武漢 430050）

斜拉橋的跨度越大，幾何非線性效應(yīng)越明顯。斜拉索的非線性主要由垂度效應(yīng)引起。為了消除垂度效應(yīng)，更準(zhǔn)確地模擬斜拉索，文獻(xiàn)[1]提出了索結(jié)構(gòu)的等效模量法，文獻(xiàn)[2]采用等效模量法考慮斜拉索垂度效應(yīng)的桿單元來模擬斜拉索，文獻(xiàn)[3]用懸鏈線單元模擬斜拉索。斜拉橋的非線性主要包括斜拉索的非線性、梁-柱幾何非線性和大位移幾何非線性[4-5]。若同時(shí)考慮這些非線性，則計(jì)算時(shí)間長(zhǎng)，效率低。因此，需要解決的問題是：①選擇兼顧精度和效率的斜拉索模擬方式；②斜拉索的非線性效應(yīng)在斜拉橋非線性效應(yīng)中所占比例。

模擬斜拉索的2種常用單元為：Ernst公式修正彈性模量的桿單元和懸鏈線單元。Ernst公式修正彈性模量的桿單元可以采用線性的切線模量法，也可以采用非線性的割線模量法，但后者計(jì)算精度和效率都低于懸鏈線單元，所以本文只研究切線模量法。切線模量法的原理：斜拉索的剛度采用上一個(gè)荷載步結(jié)束時(shí)的剛度，且在一次加載計(jì)算過程中保持不變。懸鏈線單元是非線性單元，是模擬斜拉索的最準(zhǔn)確方式，但需要迭代計(jì)算。因此，與桿單元相比，懸鏈線單元計(jì)算精度更高，但計(jì)算效率低。

本文對(duì)浩吉鐵路洞庭湖特大橋主橋采用2種單元模擬斜拉索，通過對(duì)比2種單元的內(nèi)力和剛度，研究Ernst公式修正彈性模量的桿單元在什么狀態(tài)下更接近懸鏈線單元，并對(duì)比分析其在不同工況下的計(jì)算精度和計(jì)算效率。

1 斜拉索模擬方法對(duì)比

1.1 內(nèi)力

桿單元的內(nèi)力Tb由2部分組成：①單元?jiǎng)偠染仃嚦艘怨?jié)點(diǎn)位移獲得的內(nèi)力T；②自重G產(chǎn)生的內(nèi)力在桿單元兩端均分。即Tb等于G/2與T的矢量和，在水平和豎直向的分力為Hb和Vb（圖1（a））。懸鏈線單元的內(nèi)力Ta根據(jù)平衡狀態(tài)計(jì)算得到[3，6]，其在水平和豎直向的分力為Ha和Va（圖1（b））。實(shí)際的斜拉索形狀是懸鏈線，懸鏈線單元的內(nèi)力方向在懸鏈線的切向，但桿單元的內(nèi)力方向并不在懸鏈線的切向上。2種單元的內(nèi)力存在夾角，即張拉力角度。

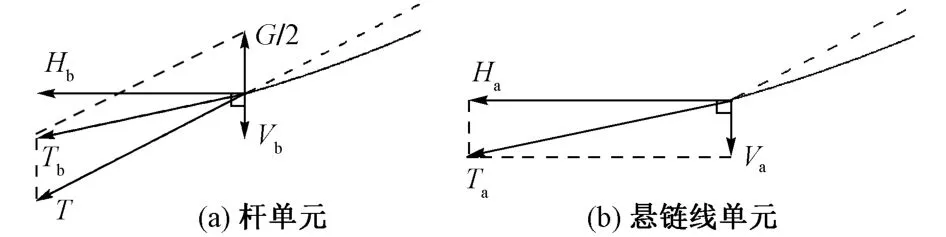
圖1 斜拉索模擬單元的內(nèi)力

以一斜拉索為例，其面積為0.001 4 m2，彈性模量E為1.9×105MPa，重度γ為78 kN/m3。桿單元張拉力Tb和懸鏈線單元張拉力Ta的大小一樣，方向不一樣。應(yīng)力、弦長(zhǎng)、傾斜角度α與張拉力角度的關(guān)系見圖2。可知：斜拉索應(yīng)力越大，斜拉索弦長(zhǎng)越短，張拉力角度越小，則采用Ernst公式修正彈性模量的桿單元模擬斜拉索越準(zhǔn)確；α=45°時(shí)，張拉力角度最大。

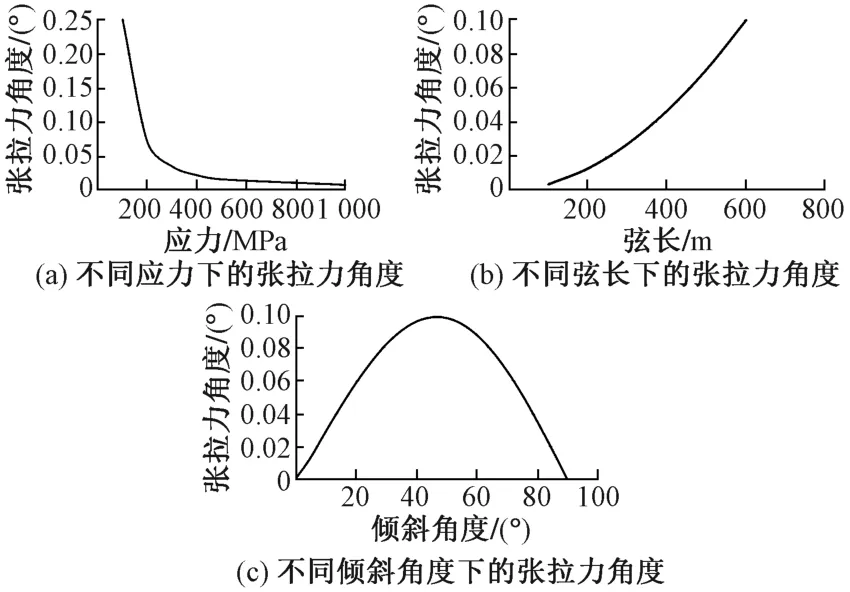
圖2 應(yīng)力、弦長(zhǎng)、傾斜角度與張拉力角度的關(guān)系

1.2 剛度

斜拉索IJ的幾何位置參數(shù)見圖3。其中，l為斜拉索水平投影長(zhǎng)度；s為斜拉索弦長(zhǎng)，l=s·cosα。

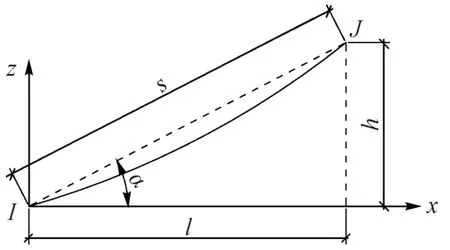
圖3 斜拉索幾何位置參數(shù)

Ernst公式修正桿單元的彈性模量Etan計(jì)算公式為

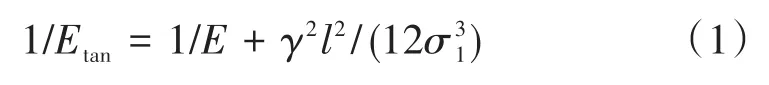
式中：σ1為斜拉索應(yīng)力。

根據(jù)斜拉索單元坐標(biāo)系（參見圖3）可知，斜拉索單元的剛度K矩陣分為4塊，即

由于KII=KJJ，KIJ=KJI=-KII，所以研究2種單元的剛度矩陣只須對(duì)比KII。參考文獻(xiàn)[6-8]可獲得懸鏈線單元的剛度，即

kxy，kyx，kzy，kyz均為 0，斜拉索IJ連線方向的剛度kL是主要?jiǎng)偠龋ㄟ^坐標(biāo)轉(zhuǎn)化將kxx，kzx，kxz，kzz轉(zhuǎn)換得到kL，可對(duì)比2種單元的剛度差異。

α=25°，s=500 m時(shí)，不同斜拉索應(yīng)力下2種單元的剛度見表1。其中，相差百分比=（桿單元?jiǎng)偠?懸鏈線單元?jiǎng)偠龋?桿單元?jiǎng)偠取Ｓ杀?可知：2種單元的剛度相差不大；斜拉索應(yīng)力越大，單元?jiǎng)偠仍酱螅恍崩鲬?yīng)力從100 MPa增加到200 MPa時(shí)，單元?jiǎng)偠仍黾恿?倍，斜拉索應(yīng)力從400 MPa增加到500 MPa時(shí)，單元?jiǎng)偠戎辉黾恿?3%。這說明斜拉索應(yīng)力越大，施工過程中斜拉索應(yīng)力變化越小，采用Ernst公式修正彈性模量的桿單元模擬斜拉索越準(zhǔn)確。

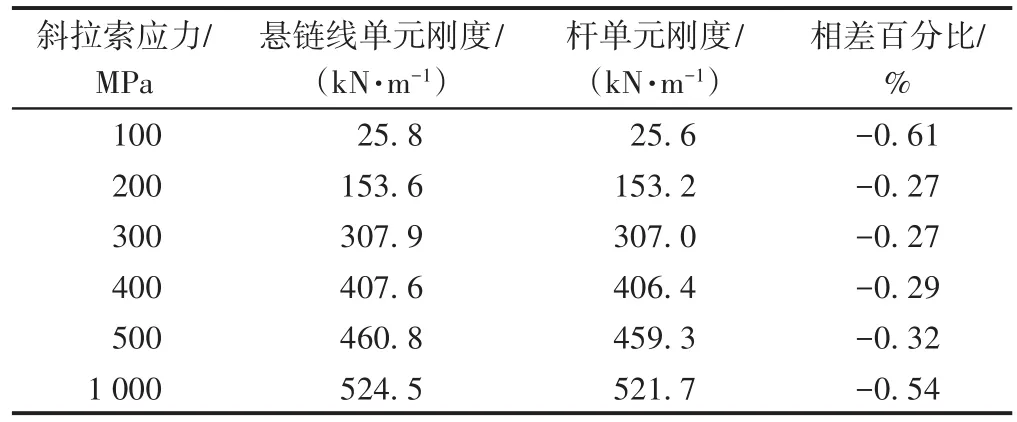
表1 不同斜拉索應(yīng)力下2種單元的剛度

α=25°，σ1=200 MPa時(shí)，不同弦長(zhǎng)下2種單元的剛度見表2。可知：2種單元的剛度相差不大；斜拉索弦長(zhǎng)越大，2種單元的剛度越小。

表2 不同弦長(zhǎng)下2種單元的剛度

s=500 m，σ1=200 MPa時(shí)，不同傾斜角度下2種單元的剛度見表3。可知：2種單元的剛度相差不大；斜拉索越接近豎直，其剛度越大。

表3 不同傾斜角度下2種單元的剛度

綜上可知：2種單元的剛度相差不大；斜拉索應(yīng)力越大，弦長(zhǎng)越短，施工過程中斜拉索應(yīng)力變化越小，則采用Ernst公式修正彈性模量的桿單元模擬斜拉索越準(zhǔn)確。

2 工程實(shí)例分析

2.1 工程概況

浩吉鐵路洞庭湖特大橋主橋?yàn)槿p索面鋼箱鋼桁結(jié)合梁斜拉橋，首次采用三塔斜拉橋和箱桁組合結(jié)構(gòu)，是浩吉鐵路煤運(yùn)通道的關(guān)鍵控制性工程。該橋全長(zhǎng)1 290.24 m，橋跨布置見圖4。

圖4 洞庭湖特大橋主橋橋跨布置（單位：m）

主梁為鋼箱鋼桁結(jié)合梁結(jié)構(gòu)，主桁采用內(nèi)傾布置，上弦和下弦中心距分別為12.0，14.0 m。全聯(lián)桁架為不帶豎桿的華倫式桁架，桁高12.0 m，節(jié)間長(zhǎng)14.0 m，斜桿立面傾角59.744°。全橋共92個(gè)節(jié)間，以4#塔對(duì)稱布置。鋼梁斷面見圖5。

圖5 鋼梁斷面（單位：mm）

施工步驟：先懸臂施工鋼箱，鋼箱合龍后再施工鋼桁。施工鋼箱時(shí)斜拉索索力比較低，斜拉索的非線性效應(yīng)較明顯。

2.2 計(jì)算模型

結(jié)構(gòu)靜力計(jì)算時(shí)，采用中鐵大橋勘測(cè)設(shè)計(jì)院集團(tuán)有限公司自編空間有限元程序3D Bridge V6建立全橋空間有限元模型。塔、梁均采用梁?jiǎn)卧M，斜拉索根據(jù)不同的計(jì)算方法采用Ernst公式修正彈性模量的桿單元和懸鏈線單元。全橋共劃分2 000個(gè)梁?jiǎn)卧?4個(gè)支承單元，1 667個(gè)節(jié)點(diǎn)。

一個(gè)典型的懸拼循環(huán)過程為：斜拉索張拉→吊機(jī)起吊下一片梁段→梁段安裝好后吊機(jī)前移至梁前端→張拉下一對(duì)斜拉索。

2.3 計(jì)算方法

為了對(duì)比Ernst公式修正彈性模量的桿單元和懸鏈線單元的計(jì)算精度和計(jì)算效率，研究斜拉索的非線性在斜拉橋非線性效應(yīng)中占的比例，采用3種方法計(jì)算主梁位移。

方法1：用Ernst公式修正彈性模量的桿單元模擬斜拉索。此方法未完全解決斜拉索的非線性問題且沒有解決其他幾何非線性問題，精度最低。

方法2：用懸鏈線單元模擬斜拉索，且不考慮其他幾何非線性的影響。此方法只解決了斜拉索的非線性問題，精度高于方法1。

方法3：用懸鏈線單元模擬斜拉索，且考慮其他幾何非線性的影響。此方法解決了所有幾何非線性問題，精度最高。

如果方法1與方法3的計(jì)算結(jié)果相差大，表明不適合采用Ernst公式修正彈性模量的桿單元模擬斜拉索。如果方法2與方法3的計(jì)算結(jié)果接近，而與方法1的計(jì)算結(jié)果相差大，表明斜拉索的非線性效應(yīng)在斜拉橋幾何非線性效應(yīng)中占主導(dǎo)地位。

2.4 計(jì)算結(jié)果

3種計(jì)算方法的橋梁結(jié)構(gòu)、邊界條件和荷載條件完全相同。選取3種工況對(duì)3種計(jì)算方法的結(jié)果進(jìn)行對(duì)比分析：①工況1（斜拉索被動(dòng)加載），E30E31箱梁段安裝，即中跨箱梁合龍前安裝最后一段箱梁；②工況2（斜拉索被動(dòng)卸載），掛設(shè)張拉13#索，即中跨箱梁合龍前掛設(shè)最后一根斜拉索；③工況3（成橋），成橋后在跨中施加300 kN的豎向荷載。

2.4.1 工況1

E30E31箱梁段安裝前后，跨中最長(zhǎng)索的應(yīng)力從236 MPa增加到298 MPa，剛度增加了1.5倍左右。E30E31箱梁段安裝前后鋼梁線形變化對(duì)比見表4。可知：①方法1的計(jì)算結(jié)果比其他2種方法的計(jì)算結(jié)果大10%左右，表明此工況不適合采用方法1。②方法2和方法3的計(jì)算結(jié)果相差不大。方法1—方法3的計(jì)算時(shí)間分別為7，9，13 s。

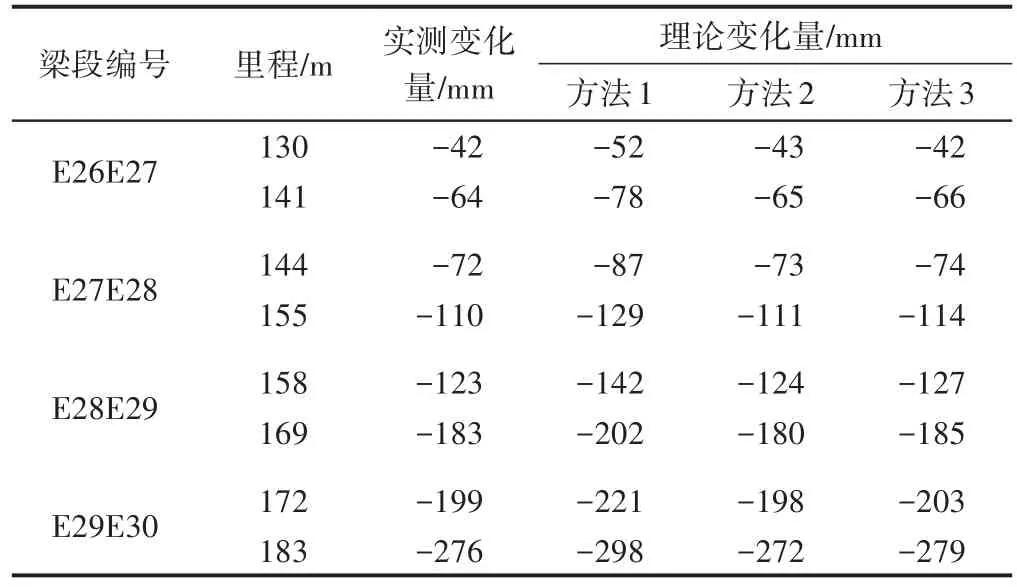
表4 E30E31箱梁段安裝前后鋼梁線形變化對(duì)比

2.4.2 工況2

掛設(shè)13#斜拉索時(shí)已經(jīng)安裝的斜拉索被動(dòng)卸載，造成應(yīng)力減小，中跨第2長(zhǎng)索的應(yīng)力從273 MPa減小到113 MPa，剛度減小50%左右。張拉13#索前后鋼梁線形變化對(duì)比見表5。可知：①方法1的計(jì)算結(jié)果比其他2種方法的計(jì)算結(jié)果小10%左右，表明此工況不適合采用方法1；②方法2和方法3的計(jì)算結(jié)果相差不大。方法1—方法3的計(jì)算時(shí)間分別為6，8，12 s。

2.4.3 工況3

成橋后在跨中加300 kN豎向荷載，方法1—方法3計(jì)算的跨中豎向位移分別為-6.31，-6.59，-6.68 mm，計(jì)算時(shí)間分別為8，10，13 s。成橋時(shí)斜拉索應(yīng)力較大，豎向荷載對(duì)索應(yīng)力的改變量不超過2 MPa，且塔直梁平，所以斜拉索的非線性效應(yīng)和其他幾何非線性效應(yīng)都不大。

表5 張拉13#索前后鋼梁線形變化對(duì)比

綜上可知：工況1和工況2不適合采用方法1；斜拉索的非線性在斜拉橋非線性效應(yīng)中占主導(dǎo)地位；工況3采用方法1能滿足精度要求且計(jì)算效率最高。

3 結(jié)論

1）斜拉索應(yīng)力越大，弦長(zhǎng)越短，施工過程中斜拉索應(yīng)力變化越小，則采用Ernst公式修正彈性模量的桿單元模擬斜拉索越準(zhǔn)確。

2）施工過程中，斜拉索應(yīng)力過小或變化較大時(shí)，斜拉索的剛度會(huì)產(chǎn)生較大的變化，采用Ernst公式修正彈性模量的桿單元誤差較大，應(yīng)采用懸鏈線單元。

3）斜拉橋成橋狀態(tài)，塔直梁平且斜拉索應(yīng)力較大，非線性效應(yīng)不明顯，采用Ernst公式修正彈性模量的桿單元能夠得到精度較高的結(jié)果。

4）斜拉索的非線性在斜拉橋非線性效應(yīng)中占主導(dǎo)地位，懸鏈線單元比Ernst公式修正彈性模量的桿單元的精度更高，但效率略低。