極限狀態法與容許應力法在鐵路橋梁設計應用中的差異性比較

鄧江濤

(中國鐵路設計集團有限公司,天津 300308)

1 概述

極限狀態法基于概率論和結構可靠度理論，考慮荷載變異、材料性能變異和工作條件的不同，采用概率統計方法和可靠度指標將各種影響因素轉化為多分項系數形式[1-4]，已廣泛應用于建筑、公路、水利、軌道交通等行業的結構設計中[5-8]；容許應力法以線性彈性理論為基礎，以構件危險截面的某一點或某一局部的計算應力小于或等于材料的容許應力為準則[5]。容許應力法設計應用簡便，是工程結構中的一種傳統設計方法，目前主要在鐵路工程設計中應用。以全預應力構件為例，綜合兩種設計方法，將控制指標分類，一般性指標對比見表1。新的鐵路橋涵極限狀態法設計已于2019年6月起正式應用在新建鐵路項目上，以概率理論為基礎、按分項系數表達的極限狀態設計方法避免了容許應力法單一安全系數過于經驗籠統、各種結構具有比較一致的安全水平等不足[9-12]，能更好地與國際接軌。

表1 全預應力構件一般性檢算指標對比

當前橋梁結構設計仍然面臨著設計規范轉軌的過渡期，還存在如計算工具滯后、實際工程應用經驗缺乏等問題，隨著新規范的不斷應用，這些問題必然會逐步得到解決，容許應力與極限狀態兩種方法在實際工程應用中的深入比較也將越來越廣泛[13-20]。

針對商合杭鐵路(48+80+48) m連續梁試設計，開展了基于極限狀態法連續梁全過程設計，通過比較分析得出了連續梁設計中的主要檢算指標相互關系以及極限狀態法與容許應力法兩種方法的差異。

2 基于極限狀態法(48+80+48) m連續梁結構設計

2.1 構造尺寸

梁全長為177.5 m，計算跨度為(48+80+48) m，中支點截面中心線處梁高6.335 m(為方便考察兩種方法的差異性，計算指標與限制的比值控制在5%以內，此處梁高為調整后的試算梁高)，跨中9 m直線段及邊跨13.25 m直線段截面中心線處梁高3.535 m，梁底下緣按二次拋物線變化。邊支座中心線至梁端0.75 m，梁縫分界線至梁端0.10 m。邊支座橫橋向中心距5.60 m，中支座橫橋向中心距5.90 m，如圖1～圖4所示。

圖1 連續梁立面(單位：cm)

圖2 連續梁平面(單位：cm)

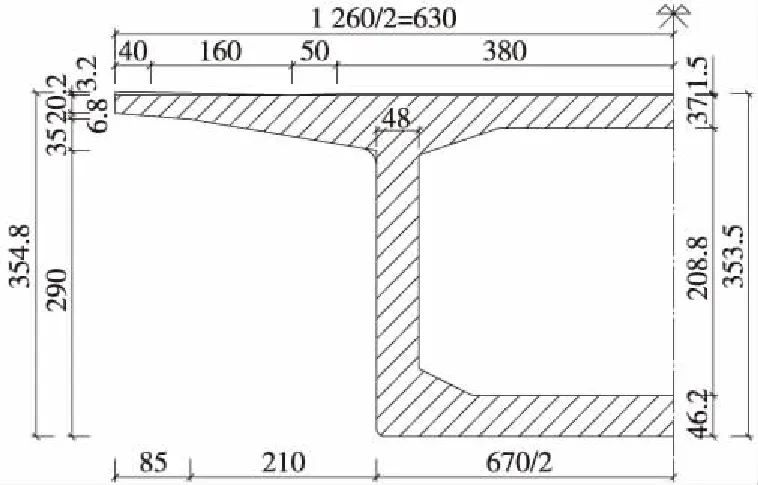
圖3 連續梁中跨跨中截面(單位：cm)

圖4 連續梁中支點截面(單位：cm)

梁體結構為單箱單室、變高度、變截面箱梁，底板、腹板、頂板局部向內側加厚，均按直線線性變化。全聯在端支點、中支點處設橫隔板，橫隔板設有孔洞，供檢查人員通過。施工方法采用懸臂施工法。

2.2 主要技術指標及主要設計荷載

設計速度350 km/h，為無砟軌道，線間距5.0 m，采用ZK活載，二期恒載按180 kN/m計，支座不均勻沉降取20 mm。

2.3 按極限狀態法檢算結果及主要指標分析

建立Midas有限元模型，全橋共計64個梁單元，提取內力，主要檢算指標如表2所示。

由表2可知，(48+80+48) m連續梁各個檢算指標均滿足規范，分析各指標富余度，對連續梁來說，起主要控制作用的檢算指標按控制程序排序為：正截面抗彎(運梁車)、正截面抗裂(運梁車)、正截面抗裂(運營)、正截面抗彎(運營)、斜截面抗彎(運梁車)、斜截面抗裂性、斜截面抗彎(運營)，對于常規連續梁，控制設計的主要指標為承載能力極限狀態下的抗彎性和正常使用極限狀態下的抗裂性，設計時應優先滿足承載能力和抗裂性兩個指標。

此外，當正截面抗彎性能滿足后，斜截面抗彎抗剪可自動滿足。截面承載能力越大，抗裂性更好，但截面承載能力滿足抗裂性并不一定滿足，尤其是在結構尺寸與鋼束配置不算富余的情況下，二者沒有一一對應的關系，設計時需要分別考慮。

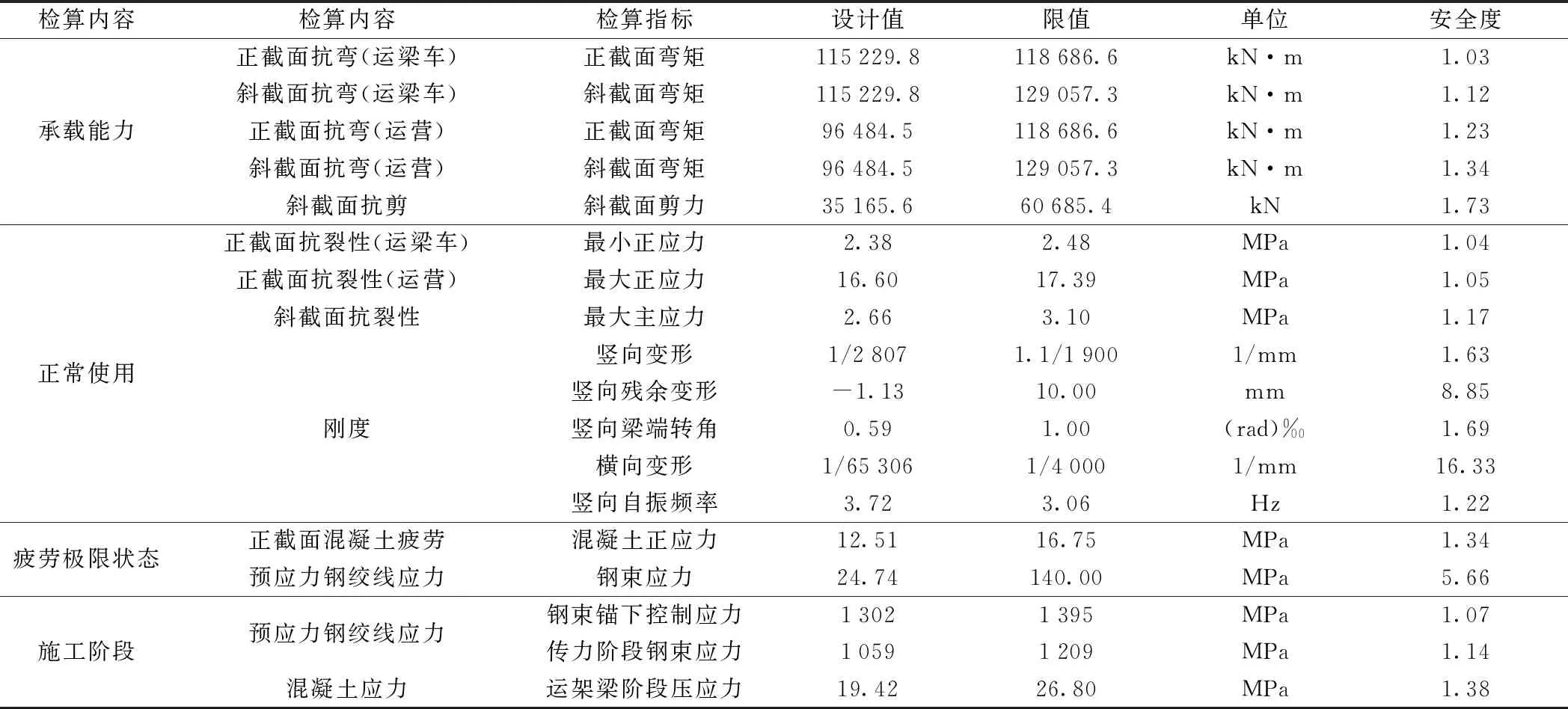
表2 極限狀態法檢算指標匯總

承載能力極限狀態下的抗彎性為主要的控制指標之一，進一步分析承載能力極限狀態，將規范里的基本組合1～基本組合6的抗力曲線如圖5、表3所示。

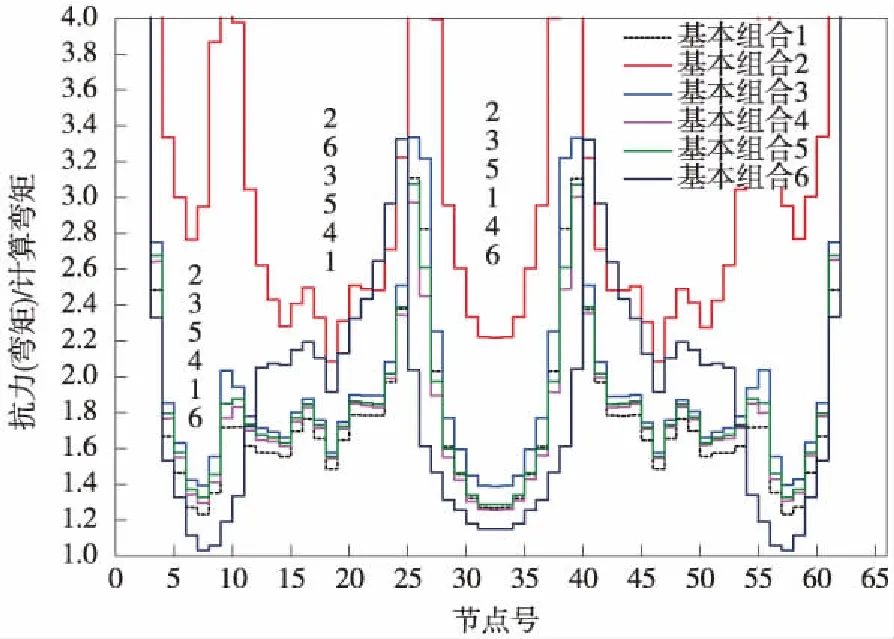
圖5 正截面承載能力對比曲線

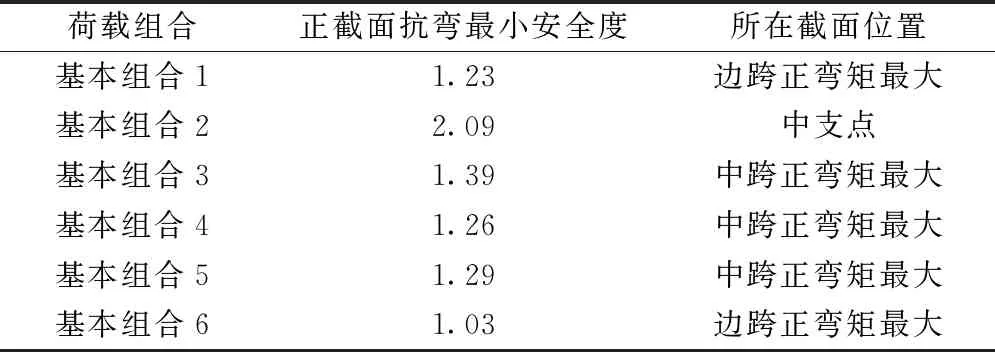
表3 承載能力指標檢算匯總

分析圖5、表3可知，在承載能力檢算中，對于邊跨正彎矩區，按照控制的程度排序為：基本組合2，3，5，4，1，6；對于中支點負彎矩區，按照控制的程度排序為：基本組合2，6，3，5，4，1；對于中跨正彎矩區，按照控制的程度排序為：基本組合2，3，5，1，4，6；由此可知，對于全梁段截面，基本組合2最不控制，基本組合1，3，4，5在各截面會因彎矩正負號有所差異，但數值相差不大。

3 極限狀態法與容許應力法對比分析

為考察極限狀態法與容許應力法兩種方法的差異性，一方面，按照第2節的結構尺寸及鋼束配置按容許應力法復算，另一方面，根據復算結果進行同精度設計，若按容許應力法檢算后結構需要加強，則按滿足1.05倍控制指標限值的原則進行加強，反之，若結構富余，同樣按滿足1.05倍控制指標限值的原則進行減少。

3.1 按容許應力法復算

采用容許應力法復算，各檢算指標匯總見表4。表4中未列出的基于運營階段使用安全考慮的豎向變形、豎向殘余變形、豎向梁端轉角、橫向變形、豎向自振頻率以及基于成橋過程安全考慮的各檢算指標與表2一致。

由表4可見，起主要控制作用的檢算指標按控制程序排序為：正截面抗彎(運梁車)、正截面抗彎(運營)、正截面抗裂(運梁車)、正截面抗裂(運營)、斜截面抗裂性、斜截面抗彎(運梁車)、斜截面抗彎(運營)，各檢算指標控制程度順序與表2結論基本一致。

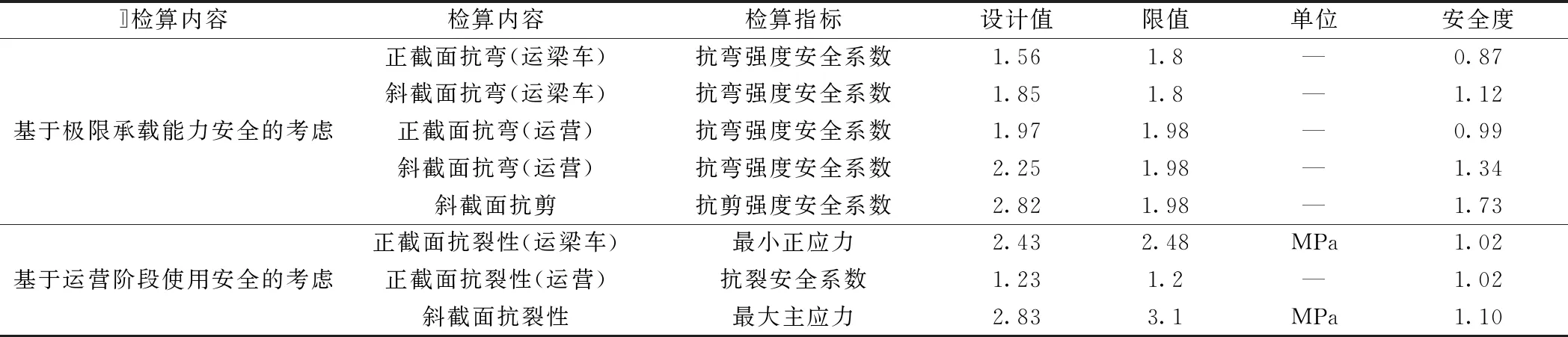
表4 容許應力法復算結果匯總

此外，按照第2節的結構尺寸及鋼束配置按容許應力法復算，運梁車工況及運營工況下的正截面抗彎強度檢算不滿足限值要求，表明容許應力法更保守，以概率理論為基礎、按分項系數表達的極限狀態設計方法，依據作用的變異性，科學采用恒載、活載、風荷載、溫度荷載等的分項系數及組合系數，使得設計結果更貼近工程實際。

3.2 按容許應力法同精度設計及經濟性對比分析

表4分析表明，采用容許應力法復算后個別指標不滿足限值要求，說明需要對結構進行加強。為進一步研究極限狀態法與容許應力法兩種方法在工程用料上的差異性，通過加強配束，來提高運梁車工況及運營工況下的正截面抗彎強度。

結構尺寸與表2所采用的一致，將邊跨底板束規格由14-φ15.2 mm調整為17-φ15.2 mm，中跨底板束規格由15-φ15.2 mm調整為18-φ15.2 mm，通過增加鋼束使正截面強度安全系數、正截面抗裂安全系數、預應力鋼束應力比的安全度達到1.05以內，各檢算指標匯總見表5，工程數量變化分析見表6。

表5 加強鋼束后檢算指標匯總

表6 縱向預應力鋼束質量及調整比例

表5、表6分析表明，通過加強邊跨底板束和中跨底板束，采用容許應力法檢算的各指標滿足規范要求，由此產生的鋼束增量為10.09 t，每聯增加比例7.7%，每聯增加工程造價約9.93萬元。

4 結論

對(48+80+48) m連續梁通過極限狀態和容許應力兩種方法試設計對比分析，可以得到以下結論。

(1)采用極限狀態法進行全過程結構設計，分析主要檢算指標，承載能力極限狀態下的抗彎性和正常使用極限狀態下的抗裂性是主要的控制指標，設計時應優先滿足。此外，當正截面抗彎性能滿足后，斜截面抗彎抗剪一般可自動滿足。截面承載能力越大，抗裂性更好，但截面承載能力滿足抗裂性并不一定滿足，尤其是在結構尺寸與鋼束配置不算富余的情況下，二者沒有一一對應的關系，設計時需分別考慮。

(2)按容許應力法復算，運梁車工況及運營工況下的正截面抗彎強度檢算不滿足限值要求，表明容許應力法更保守，以概率理論為基礎、按分項系數表達的極限狀態設計方法，依據作用的變異性，科學采用恒載、活載、風荷載、溫度荷載等的分項系數及組合系數，使得設計結果更貼近工程實際。

(3)按容許應力法同精度設計，通過加強邊跨底板束和中跨底板束，采用容許應力法檢算的各指標滿足規范要求，增加鋼束用量10.09 t，增加7.7%，每聯工程造價增加約9.93萬元。