基于屈曲分析的連桿截面參數優化

郭旭陽，陳宇，徐琳，韋靜思，占文鋒

(廣州汽車集團股份有限公司廣汽工程研究院，廣東 廣州 511434)

發動機工作過程中，連桿主要承受氣體壓力和慣性力交變負荷，因此，在設計連桿時，首先要保證其有足夠的疲勞強度和結構剛度。桿身剛度不足時，在壓縮載荷作用下，會引起平行和垂直于曲軸軸線平面內的彎曲，制造連桿時，如有初始彎曲和偏心，以上情況會加劇[1]。

為了增加連桿的強度和剛度，不能簡單加大結構尺寸，因為連桿質量的增加使慣性力相應增加。因此，對于連桿的設計，要求在盡可能輕巧的結構尺寸下保證足夠的剛度和強度[2]。

在高性能發動機的開發中，燃氣燃燒壓力呈逐漸上升趨勢，邊界條件越來越苛刻，對連桿強度和剛度提出很大的挑戰。同時，由于排放法規收嚴和降油耗目標，要求盡量減小曲柄連桿機構質量，實現輕量化設計。傳統的經驗優化設計已不能滿足輕量化設計需求，如何采用參數化的優化方法，在指定條件下獲得最優設計方案尤為重要。

連桿疲勞危險位置主要在大小頭過渡區域，其優化方法一般為局部形狀優化，對質量影響較小，研究較為成熟。而屈曲變形發生在桿身部位，桿身連接大小頭端，其方案設計對質量影響很大，國內研究較少。為了在較小質量下得到較大的剛度，高速內燃機的連桿桿身的斷面都是“工”字形的，而且其長軸應在連桿擺動平面內。這是由于連桿在擺動平面內上下兩端的連接相當于鉸支，而在垂直連桿擺動平面內上下兩端的連接相當于兩端固定的壓桿[3]。有文獻指出，減小工字梁翼板和腹板的厚度可提高抗屈曲性能，腹板最小厚度2.3 mm[4]，但缺少具體理論和計算分析。有學者進行了考慮桿身屈曲優化的研究，但沒有具體方法和指標說明[5-6]。

本研究以某高強度汽油機連桿為例，采用試驗設計(DOE)方法開展工字梁結構參數敏感性分析，提取對質量和屈曲貢獻度大的參數，進行基于NLPQL算法的參數優化，實現連桿的最優輕量化設計。

1 理論分析

1.1 壓桿屈曲理論

壓桿屈曲計算根據柔度值分為大柔度桿、中柔度桿、小柔度桿，并采用不同的計算公式[7]。

1) 當λ≥λp時，壓桿為長柔度桿，采用Eular公式：

(1)

2) 當λs≤λ<λp時，壓桿為中柔度桿，多采用經驗公式：

σcr=a-bλ。

(2)

3) 當λ<λs時，壓桿小柔度桿，按強度條件進行計算：

σcr=σs。

(3)

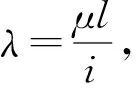
對于小柔度桿，其受到的破壞是由于壓應力達到屈服極限而引起的，因此，采用屈服強度準則進行計算。

1.2 Neuber理論

連桿截面應力直接計算結果為線彈性應力應變，采用Neuber方程將其轉化為彈塑性狀態應力應變。構件局部區域在大載荷作用下進入彈塑性狀態，應力應變不再是線性關系，此時需考慮塑性應變影響。將彈性的應力應變轉化為彈塑性應力應變，工程上普遍采用Neuber法或Neuber修正法[8-9]。Neuber提出的計算缺口的根部彈塑性應力應變方程為

(4)

式中：KT為理論應力集中系數；Kσ=σ/S為應力集中系數，σ為缺口根部的局部應力，S為名義應力，當構件處于彈性狀態時，Kσ=KT；Kε=ε/e為應變集中系數，ε為缺口根部的局部應變，e為名義應變。當構件處于彈性狀態時，

(5)

名義應力和名義應變之間為彈性關系，S=Ee，代入式(4)得：

(6)

式中：C為Neuber常數；E為彈性模量。

本研究通過壓縮試驗獲得連桿材料真實的應力應變曲線，根據式(4)將計算所得的名義應力轉化為彈塑性狀態下的局部應力(見圖1)。

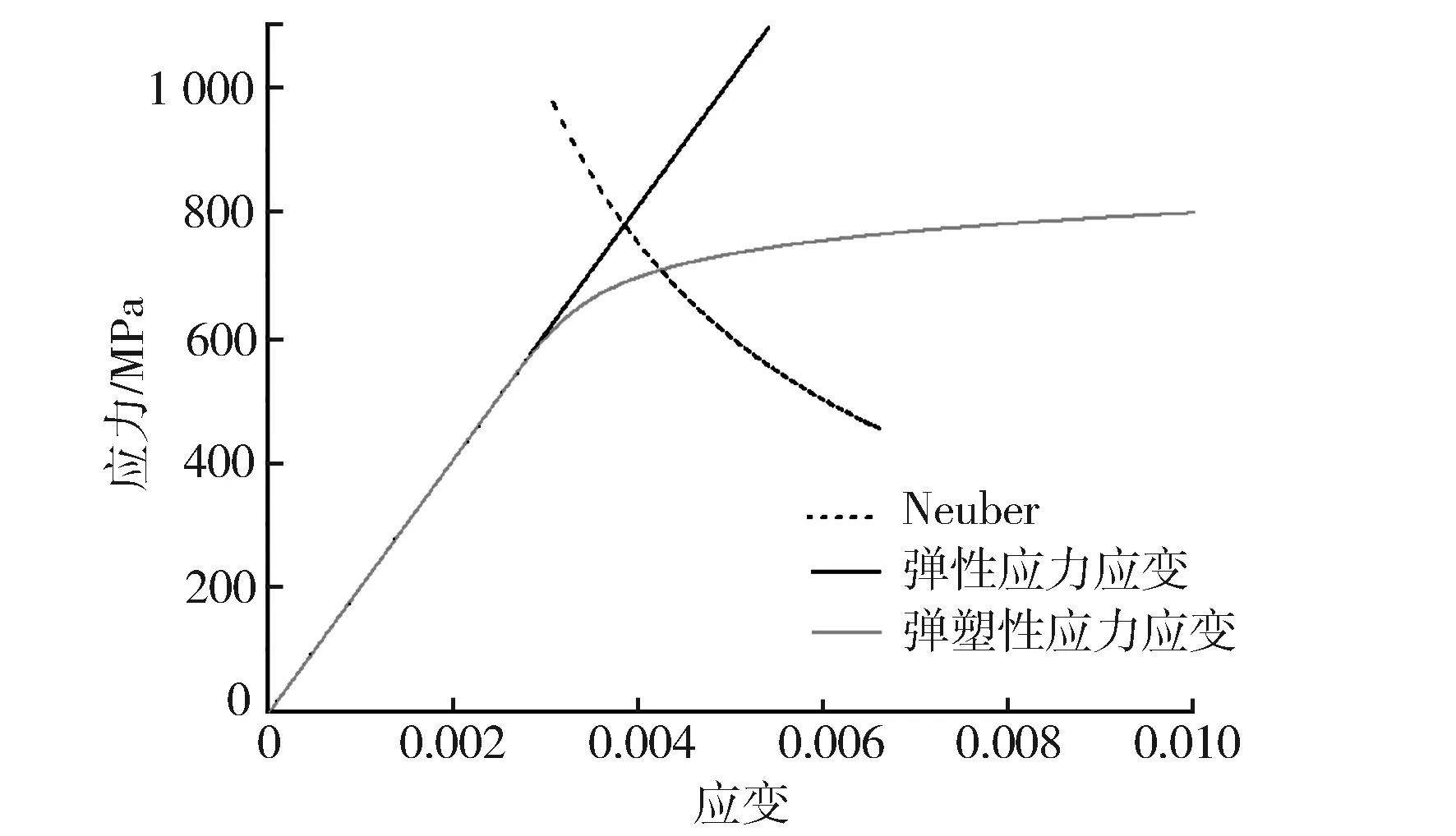
圖1 材料應力轉換曲線

1.3 NLPQL參數優化算法

NLPQL(序列二次規劃)算法具有穩健性好、優化效率高的優點，是求解帶有約束的非線性數學規劃問題最有效的方法，在實際工程設計問題中應用廣泛。將目標函數以二級泰勒級數展開，并把約束條件線性化，通過解二次規劃得到下一個設計點。然后根據兩個可供選擇的優化函數執行一次線性搜索，其中Hessian矩陣由BFGS公式更新[10]。

尋找x=(x1,x2,…xn)，

設計變量

使得F(x)最小，

目標函數

gi(x)=0i∈E={1,2,…me}，

等式約束

gi(x)≥0i∈I={me+1,…m}，

不等式約束

xl≤x≤xu。

邊界約束

作為一種迭代算法，NLPQLP是在每次迭代中求解一個對原問題近似的二次規劃子問題。子問題的目標函數是原問題的Lagrange函數的二次近似，約束條件是原問題約束函數的線性近似：

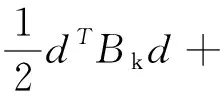
gi(xk)Td+gi(xk)=0i∈E，
gi(xk)Td+gi(xk)≥0i∈I，
xl-xk≤d≤xu-xk。

為了讓算法更加穩定，尤其是在起始點X0不理想的情況下，要保證達到全局收斂，在NLPQL中應用了附加線性搜索，算法穩定。

2 參數優化模型

2.1 設計變量

根據連桿桿身結構設計特點，對工字梁的截面進行參數化：翼板寬度A1,翼板厚度B1，腹板寬度A2,腹板厚度B2，過渡圓角半徑R1、R2、R3，拔模角α，共8個設計變量(見圖2)。

圖2 連桿截面參數

受鍛造工藝影響，拔模角不可變更，本研究不考慮拔模角的影響。確定設計范圍需要考慮以下因素：截面兩壁過薄或圓角過小，容易導致鑄造過程桿身邊緣出現裂紋；翼板寬度A1和翼板厚度B1不能過大，保證連桿運動包絡不受干涉。本研究以開發中的某汽油機連桿為研究對象，參數設計見表1。

表1 連桿截面優化設計參數

2.2 優化目標及約束

連桿的截面設計直接影響抗屈曲能力和輕量化水平。屈曲與截面面積及慣性矩相關，桿身質量與截面面積直接相關。桿身截面面積A，慣性矩Ix和Iy與設計變量之間的關系通過編程獲得。

截面設計優化的目標是在保證不發生屈曲條件下，連桿桿身質量最輕。其數學表達式如下:

安全系數SF表征抗屈曲能力的大小。連桿屈曲計算方法需要根據柔度確定連桿類型。按照表1中初始設計方案計算連桿擺動平面和垂直擺動平面柔度，計算結果見表2。由表2可見，連桿為小柔度桿，需要按照屈服強度準則計算屈曲，并且垂直擺動平面的柔度略大于擺動平面柔度，風險更大。根據尺寸鏈公差計算得到曲柄連桿機構沿活塞軸線的最大偏心量。偏心量的存在會大大減小連桿垂直擺動平面屈曲臨界載荷。因此本研究進行了垂直擺動平面的屈曲研究，并考慮偏心量的作用。

表2 柔度計算結果

由于連桿為小柔度桿，高燃燒壓力導致的高應力水平作用使得桿身薄弱區域的應力應變不再呈線性關系。如直接采用線性分析則誤差較大，通過Neuber法將彈性應力轉化為彈塑性應力，屈曲安全系數的計算公式如下：

(7)

式中：σs為材料屈服強度；σe-p為連桿截面彈塑性狀態應力，需要把計算出的彈性應力經過Neuber公式進行轉換：

(8)

(9)

(10)

式中：e為偏心量；Ix為對X軸慣性矩；D為發動機缸徑；Pmax為最大屈曲燃燒壓力。在此邊界條件下，屈曲安全系數要求不小于1.1。

3 敏感性分析及優化

3.1 敏感性分析

影響連桿屈曲性能的主要參數包括材料壓縮彈性模量、泊松比、應力應變曲線、連桿截面尺寸和桿長。連桿材料為46MnVS5，為提高計算精度，從連桿本體取樣獲取試棒進行軸向壓縮試驗，得到材料壓縮彈性模量(203 GPa)和應力應變曲線(見圖3)。0.2%塑性應變對應的屈服強度取5個試棒結果的平均值，為750 MPa。

圖3 連桿材料性能

首先對參數進行敏感性分析，根據計算結果判斷各個參數對屈曲的貢獻度。各設計參數的上下限按照表1給出的邊界確定為高水平和低水平，并取中間值作為中間水平。七因子三水平的全因子正交試驗需要進行L2187(37)次試驗，試驗次數多，計算量大。為提高計算效率，減少試驗次數，并使正交表盡量覆蓋保證計算精度，采用L27(37)的田口正交設計，分別計算截面上最大彈塑性應力和截面面積，并對結果進行主效應和敏感度分析。

從圖4應力主效應圖看出，隨參數A1，B1，R1，R2水平增加應力減小，隨參數A2，B2增加應力增大，隨參數R3水平增加應力先增大后減小。從圖5面積主效應圖看出，隨參數A1，B1，B2，R1水平增加面積增大，隨參數A2，R2，R3水平增加面積減小。說明增大翼板厚度和寬度可以減小應力，提升抗屈曲能力，但會使質量增加很多；而增大腹板寬度可以減重，但會使應力提升。

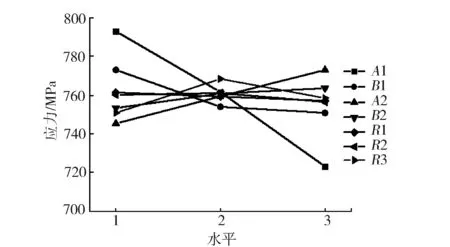
圖4 應力主效應圖

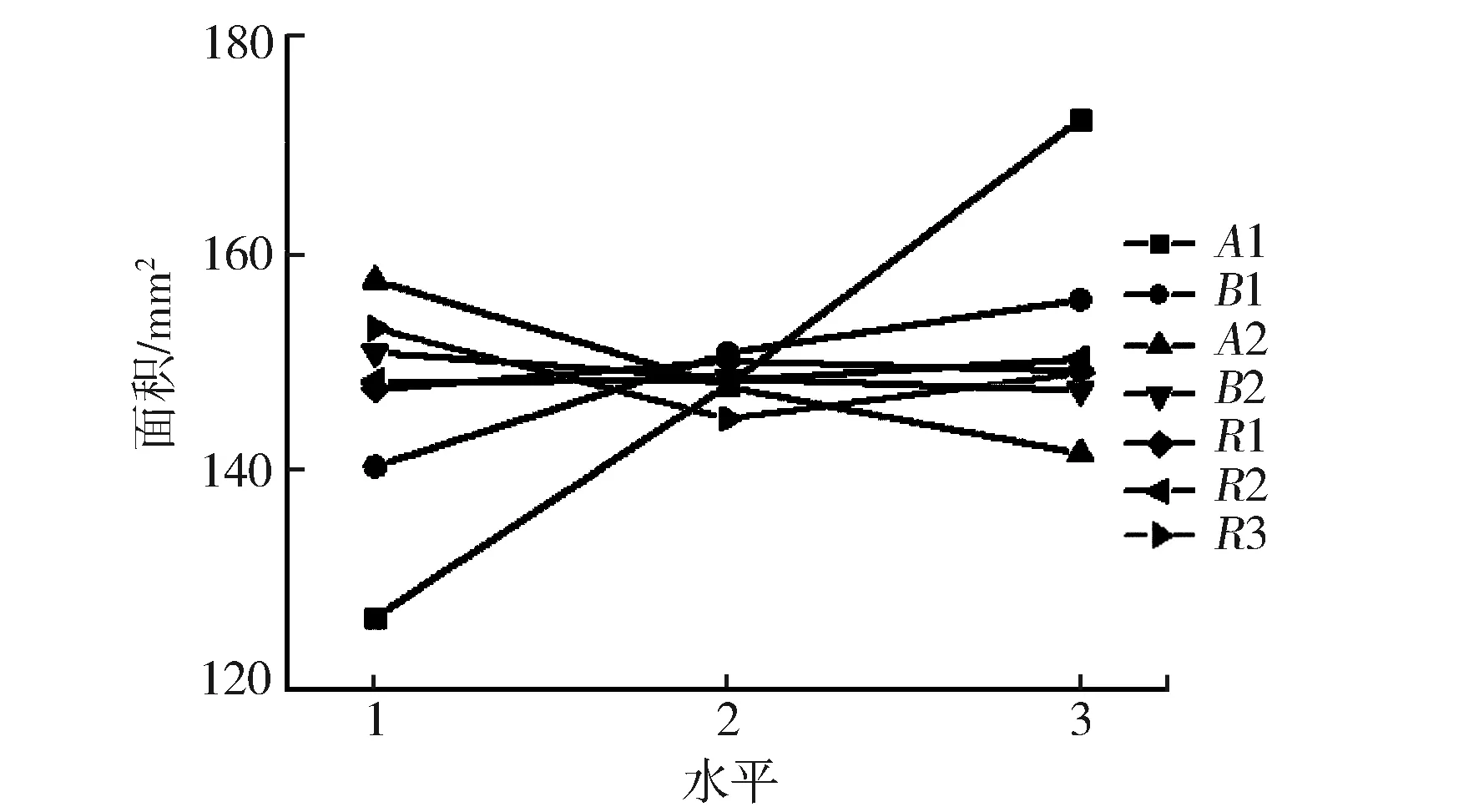
圖5 面積主效應圖

從圖6和圖7敏感性結果看出，A1，B1，A2，R3這4個因素對屈曲應力較敏感，R1，R2和B2對屈曲應力不敏感，而A1，B1，A2 這3個因素對面積較敏感。故優化過程中重點考慮A1，B1，A2，R3 4個因素的影響。

圖6 應力敏感性結果

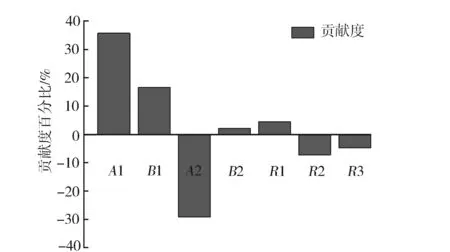
圖7 面積敏感性結果

3.2 連桿截面優化

為了追求輕量化設計，連桿初始截面尺寸設計較激進，不滿足屈曲要求，工作過程中當燃燒壓力較大時連桿存在桿身壓彎的風險。因此，需要對截面進行優化設計，使其既滿足屈曲要求，又滿足質量要求。根據敏感性分析結果，對A1，A2，B1，R3進行參數優化。考慮到建模和鍛造要求，取B2=2.65 mm，R1=3 mm，R2=1.5 mm。A1限值為[19，22]，B1限值為[12，14.2]，A2限值為[9，12]，R3限值為[1.5，3]。

為研究不同參數對目標函數和約束指標的影響，采用最優超拉丁方設計獲取30組關于4個參數與安全系數和截面積的試驗數據，構建二次響應面模型。設截面積為y1，屈曲安全系數為y2，A1，A2，B1，R3截面參數分別為x1，x2，x3，x4，其響應面模型為

y1=6.16+2.65x2-0.49x3-
0.76x42+x1x3-x2x3，

(11)

y2=0.01(160.71-8.16x1+7.37x2-7.29x3+
2.89x4+0.17x12+0.13x22+0.15x32-
0.2x42-0.29x1x2+0.54x1x3-0.13x1x4-
0.5x2x3+0.09x2x4-0.09x3x4)。

(12)

優化目標y1和約束指標y2隨4個截面參數的變化情況見圖8和圖9。由圖可見，隨翼板寬度A1和翼板厚度B1增大，屈曲安全系數顯著增加，但面積也顯著增加；隨腹板寬度A2和翼板外側過渡圓角R3增大，屈曲安全系數降低，但面積有所減小。提升截面抗屈曲能力可通過增大A1，B1，減小A2，R3實現；輕量化設計可通過減小A1，B1，增大A2，R3實現。

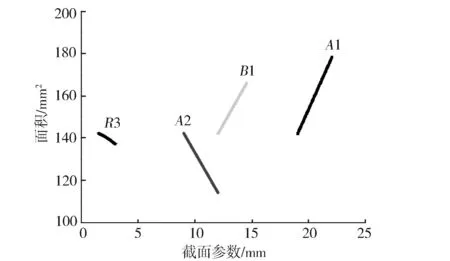
圖8 面積隨截面參數變化情況

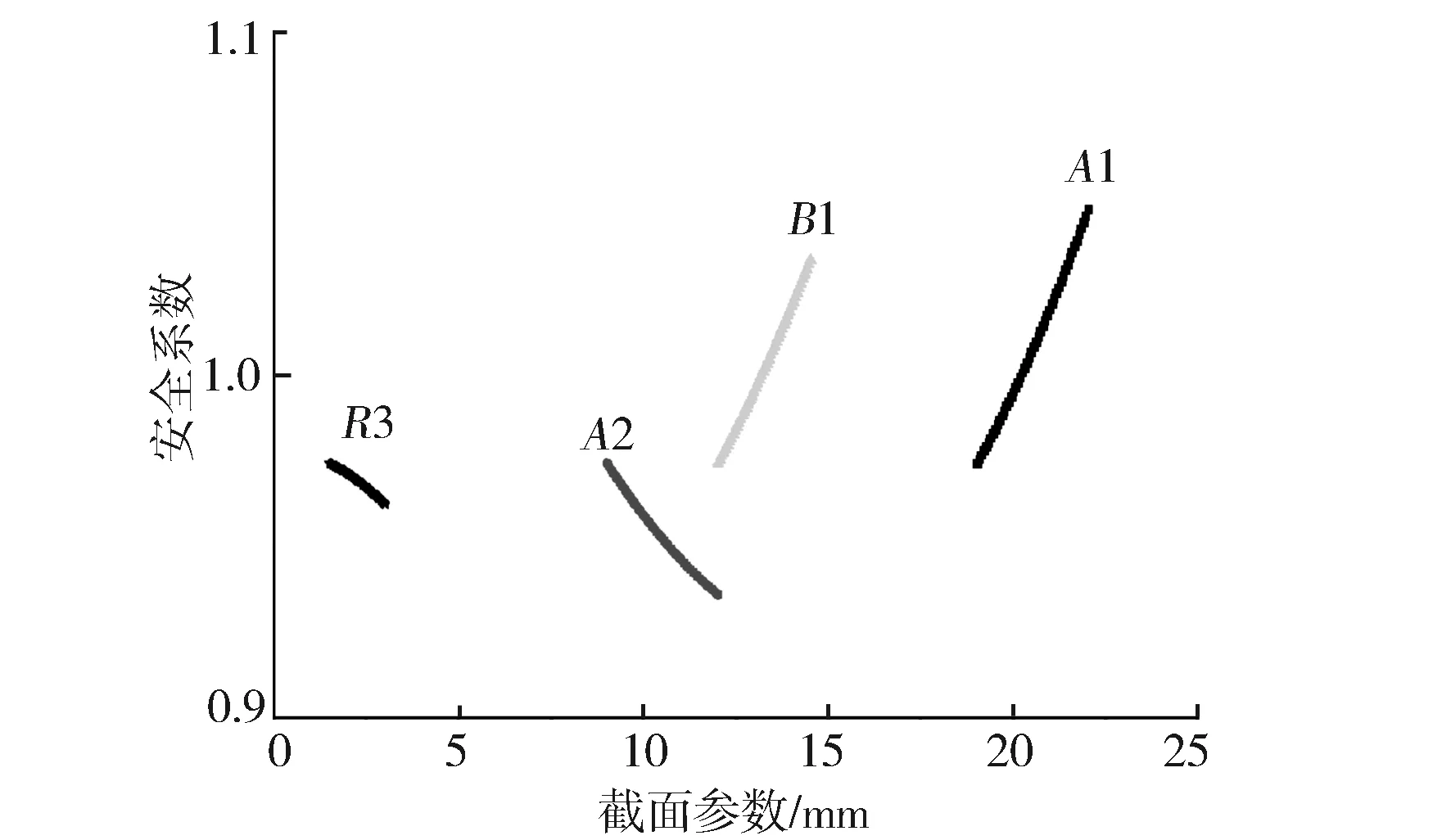
圖9 屈曲安全系數隨截面參數變化情況

采用Isight搭建模型(見圖10)，優化目標為截面面積最小，約束指標為屈曲安全系數達到1.1。

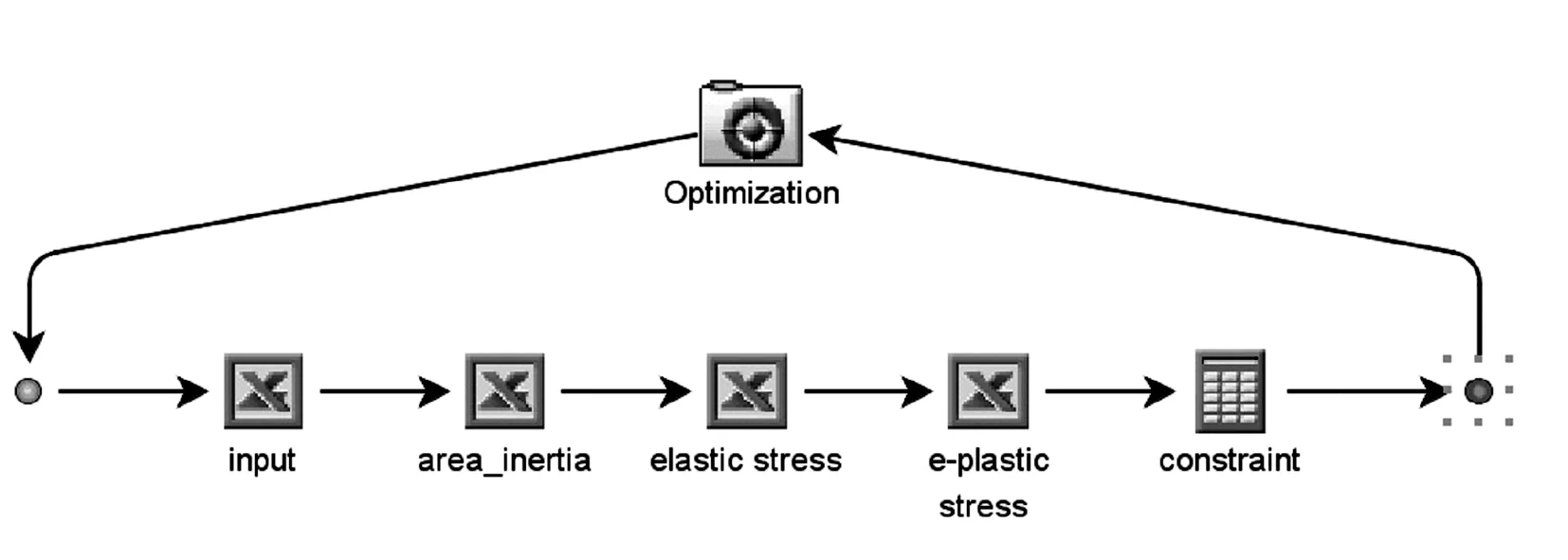
圖10 Isight參數優化模型

優化算法選擇NLPQLP，最大迭代次數設置為50次，計算迭代過程見圖11。迭代次數達到20次時得到了最優解，應用該優化算法收斂速度快、穩健性好。

圖11 迭代過程

優化前后的計算結果見表3。對比優化前后計算結果，在約束邊界條件下，優化計算通過減小A1，A2，增大B1和保持R3不變，將安全系數從優化前的1.05提高到優化后的1.1，提升約5%，截面積(S)略有增加，既保證了抗屈曲性能，又達到輕量化設計要求。如按照經驗設計，一般通過加大截面尺寸提高截面抗屈曲能力，但會使連桿質量大大增加。

表3 優化前后結果對比

4 連桿屈曲有限元分析

為驗證截面優化的有效性，對連桿基于截面進行重構設計，對優化前和優化后的連桿進行屈曲仿真分析。仿真模型既考慮截面、長度等尺寸設計的影響，同時考慮沿活塞銷周向偏心量作用。優化前后連桿模型長度未變化，僅截面及大小頭過渡區域發生變化，因此通過有限元分析可以評估截面抗屈曲能力。基于Abaqus中的Riks分析步進行，有限元模型包括活塞銷、襯套、連桿、軸瓦、螺栓，網格單元類型為C3D10M，大頭孔中心點與軸瓦內側120°面剛性耦合，約束大頭孔中心點。有限元仿真模型見圖12。

圖12 有限元仿真模型

輸出大頭孔中心點支反力轉化為缸內壓力值，以此作為Y軸，取連桿截面PEEQ最大位置的塑性應變作為X軸，計算結果及連桿屈曲形態見圖13。由圖13可見，優化前連桿屈服對應的壓力為19.6 MPa，失穩對應的極限壓力為20.8 MPa；優化后連桿屈服對應的壓力為 22.4 MPa，失穩對應的極限壓力為24.1 MPa。優化后，連桿抗屈服能力提升了14%，抗極限失穩能力提升了16%，連桿的抗屈曲能力大幅提高，驗證了截面參數優化的有效性。

圖13 有限元屈曲結果

5 結論

a) 采用試驗設計可快速識別出對屈曲應力和截面面積敏感的參數，篩選出貢獻度大的參數進行優化計算，大幅提高了優化效率；

b) 利用Isight搭建基于A1，B1，A2，R3共4個參數的優化模型，以NLPQLP優化算法計算得到最優方案，定量地實現屈曲安全系數達到1.1和質量最小的目標；提出的優化方法實現了連桿設計從定性分析到定量分析的轉換；

c) 對優化前后的連桿進行Riks屈曲仿真計算，結果表明，優化后連桿抗屈服能力提升了14%，抗極限失穩能力提升了16%，連桿的抗屈曲能力大幅提高，驗證了截面參數優化方法的有效性；連桿屈曲優化分析方法在概念設計階段應用，對于實現連桿輕量化設計，預防屈曲問題具有積極有效的指導意義。