四足機器人trot 步態聯合仿真分析

吳潯煒，左鵬

（200093 上海市 上海理工大學 機械工程學院）

0 引言

在眾多應用場景中，盡管輪式、履帶式機器人滿足了人們的諸多需求，但是輪式及履帶式的結構也決定了其在非結構化路面等復雜環境下的運動能力欠缺。相比之下，足式機器人由于能夠選擇離散的落足點而使得其在復雜路面下的通過能力遠高于輪式機器人，其中四足機器人具有更好的綜合性能[1]。

本文設計一個四足機器人，利用SolidWorks建立四足機器人的簡化模型，在ADAMS 中建立虛擬樣機，設置環境模擬量模擬四足機器人在現實環境中的運動和狀態，利用MATLAB 和ADAMS 聯合仿真的方法對四足機器人進行運動仿真，根據仿真結果對設計方案進行優化，提高機器人結構的合理性。與其他步態相比，trot 步態具有較寬的速度變化，并且可在支撐相和擺動相之間平滑切換。行走時有較好的對稱性，有效地消除了機器人軀干的不平衡力矩[2-3]。本文利用trot 步態進行四足機器人仿真。

1 四足機器人結構

在ADAMS 軟件中難以實現復雜結構的建立，所以在SolidWorks 中建立三維模型，通過中間格式將三維模型導入ADAMS 中進行仿真。四足機器人采用仿四足動物的身體結構形式，四足機器人由機身以及4 條腿組成。

腿機構的可控自由度越多，機器人的靈活性就越好，但每一個可控自由度要配備一套驅動系統和一套傳動機構，所以每增加一個自由度，其質量相應要增加許多，因此步行機器人腿機構的自由度在滿足運動條件前提下越少越好。這里選定每條腿有3 個空間自由度，即機器人每條腿具有3 個關節，分別為側擺關節、髖關節和膝關節。關節配置形式采用全肘式。全肘式的關節配置更利于在復雜的地面上行走，具有很好的穩定性[4]。根據以上分析，建立四足機器人結構三維圖，如圖1 所示。

在相同的關節輸出力矩的情況下，腿的質量/轉動慣量越小，則被控響應速度越快。另一方面，機器人在從高處下落這種情況時，腿著地瞬間，關節速度瞬間突變。如機器人腿的轉動慣量過大，將會給腿連桿產生較大的沖擊力矩，而損壞腿或足。尤其是如果采用較高減速比的減速器來驅動關節，那么電機轉子本身的轉動慣量等效到腿關節上后將會很大，使得在關節速度突變這種情況下，很容易損壞減速器。

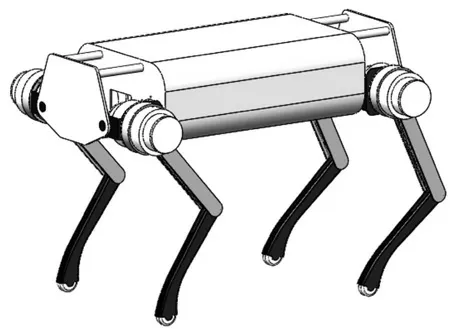
圖1 四足器人三維模型Fig.1 3D model of quadruped robot

為了有效減小機器人腿的質量，一般通過傳動機構將膝關節的電機挪至髖關節處。如圖2 所示，本文結構將膝關節電機移至髖關節，并通過鏈傳動驅動膝關節運動。

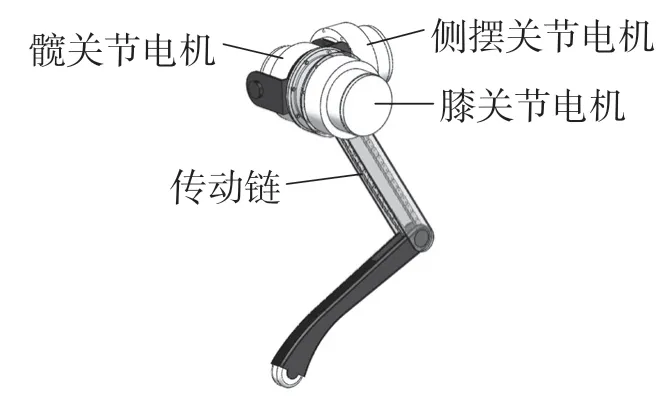
圖2 左前腿三維模型Fig.2 3D model of left front leg

2 單腿運動學建模

2.1 運動學正解

運動學模型是對四足機器人運動控制以及分析的基礎。圖3 所示機構參數為：L1為髖部長度，即橫擺中心到大腿旋轉中心的距離；L2為大腿長度；L3小腿長度；θ1為側擺轉角；θ2為髖關節轉角；θ3為膝關節轉角。

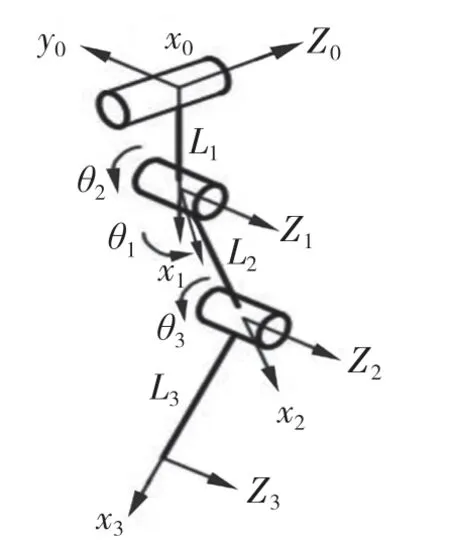
圖3 單腿D-H 坐標圖Fig.3 D-H coordinate diagram of single leg

在橫擺中心處建立基坐標系，利用D-H 坐標表示法建立足端坐標系在基坐標系下的坐標，見表1。

表1 單腿D-H 坐標參數Tab.1 D-H coordinate parameters of single leg

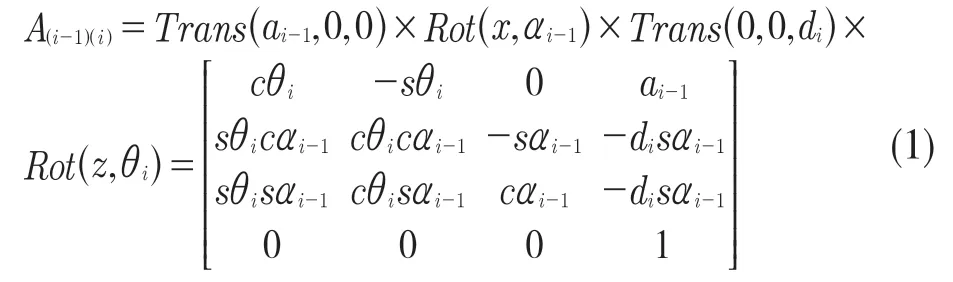
連桿變換通式：

將表1 數據帶入式（1）的連桿間可得變換矩陣為

足端位姿相對于基坐標系，可得變換矩陣為

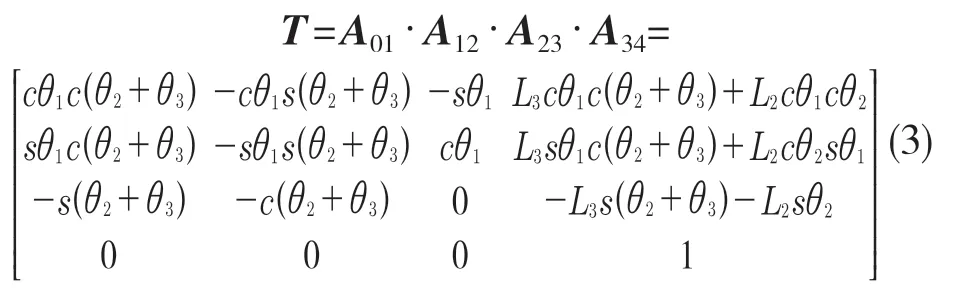
若只考慮足端位置，不考慮姿態，則足端位姿相對于基坐標系的變換矩陣為

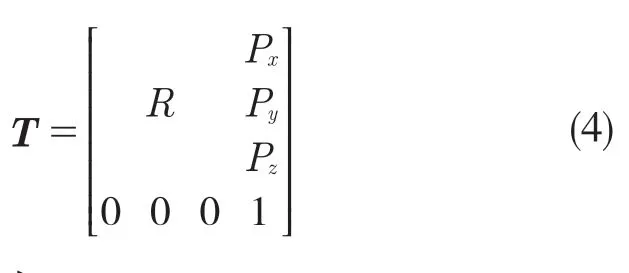
則單腿正解為

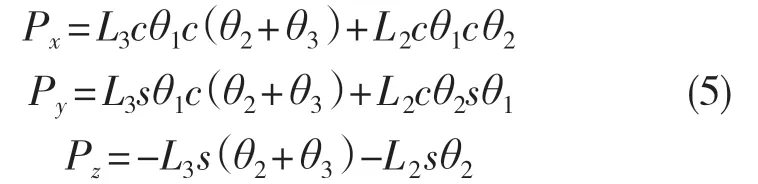
2.2 運動學逆解

對四足機器人正運動學方程進行反解可得出逆運動學方程，即根據足端坐標求出關節角度。

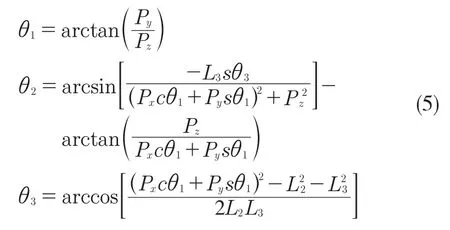
3 ADAMS 建模與聯合仿真

3.1 ADAMS 建模及輸入輸出變量設置

在ADAMS 中進行四足機器人動力學仿真，需要將SolidWorks 的三維圖以x_t 格式保存，然后導入到ADAMS 中，如圖4 所示。在ADAMS 中，定義各個部件之間的約束關系。機器人總自由度數為12 個，故在每個關節都添加一個轉動副，并且在轉動副上添加旋轉驅動作為輸入。四足機器人與環境的作用關系僅通過足端與地面的相互作用實現，故在足端與地面之間應設置接觸力，具體接觸力參數設置如圖5 所示。

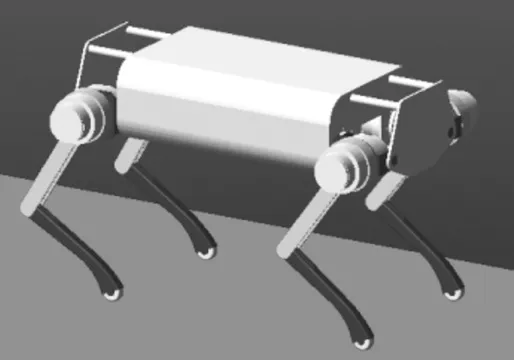
圖4 機器人虛擬樣機模型Fig.4 Robot virtual prototype model

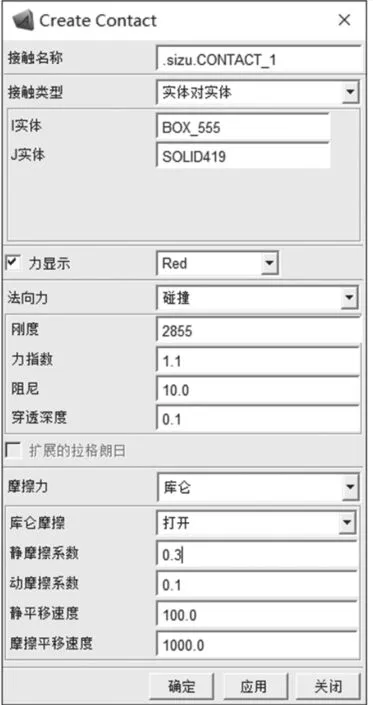
圖5 接觸力參數設置Fig.5 Contact force parameter setting

本文設計的四足機器人采用電機驅動關節的形式，故輸入為各條腿的3 個關節驅動，總共12 個驅動。輸出為機體質心在3 個方向上的位移，以及左前腿髖關節和膝關節的扭矩。利用Element 建立系統輸入輸出變量，定義LF1、LF2、LF3、LB1、LB2、LB3、RF1、RF2、RF3、RB1、RB2 和RB3 為各個關節的輸入變量，利用VARVAL 函數作為驅動的輸入。定義DX，DY，DZ，pitch，roll，yaw，Torque1 和Torque2作為輸出變量，其中DX，DY，DZ 分別為質心在豎直方向、橫向和前進方向這3 個方向上的位移量；pitch，roll，yaw 分別為機體的俯仰角、橫滾角、偏航角；Torque1 和Torque2 為左前腿髖關節和膝關節的扭矩。將虛擬模型的機械系統導出，如圖6 所示。

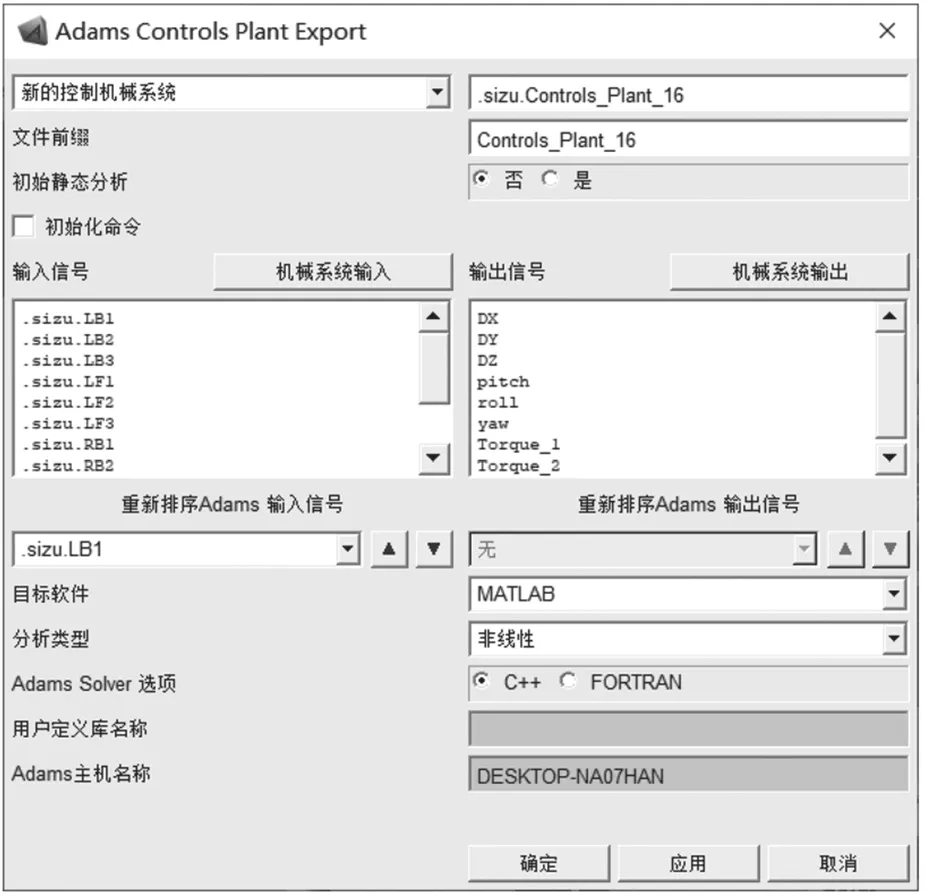
圖6 輸入輸出設置窗口Fig.6 Input and output settings window

3.2 聯合仿真平臺搭建

為實現四足機器人穩定行走，需要實時地對四足機器人狀態進行分析和控制。ADAMS 和MATLAB 的聯合仿真可實現這一過程。整個過程中ADAMS 中虛擬樣機作為被控制對象，需要從MATLAB 中獲得驅動數據，即MATLAB 的輸出為ADAMS 的輸入。MATLAB 則需要虛擬樣機的實現狀態來調整控制程序，即ADAMS 中虛擬樣機的狀態輸出為MATLAB 的輸入。圖7 是從ADAMS 中導出的機械系統，其輸入輸出在上文中進行了說明。圖8 為四足機器人的整個控制程序，將每條腿的控制程序作為子系統進行封裝，每條腿的3 個輸出作為機器人機械系統的輸入。

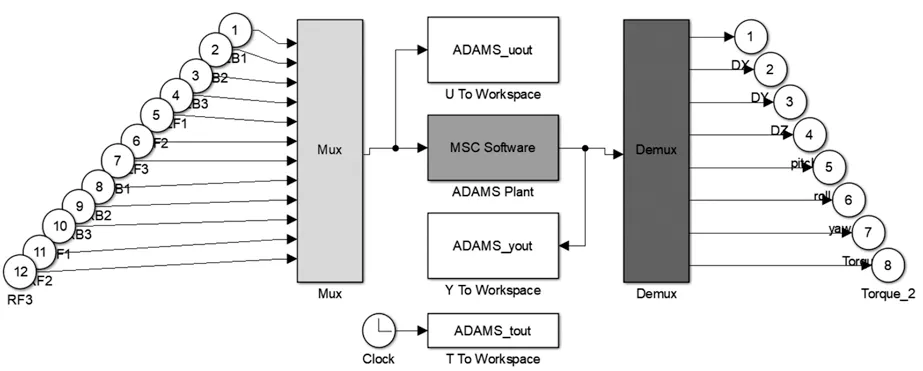
圖7 ADAMS 機械系統Fig.7 ADAMS mechanical system

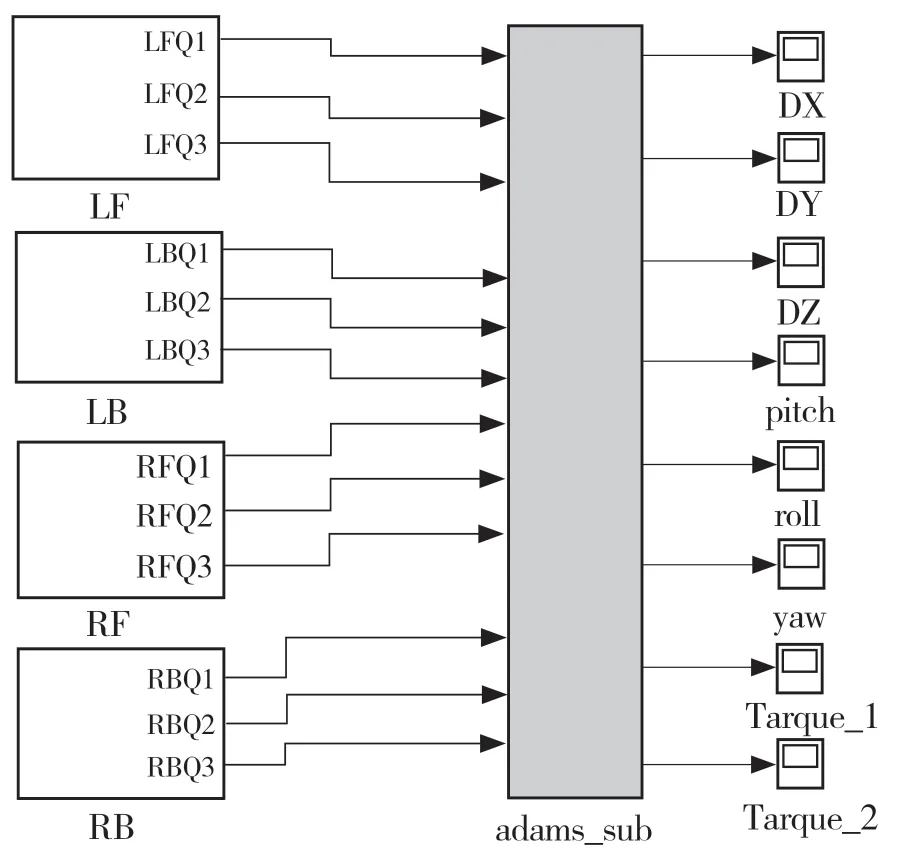
圖8 Simulink 控制系統Fig.8 Simulink control system

4 仿真分析

仿真過程共持續6 s。為獲得更好的運動效果，本文采用五次多項式軌跡進行足端軌跡規劃，并在機器人行走前對4 條腿的初始位置進行調整，使得在行走過程中，重心相對于支撐腳連線的運動盡量保證前后對稱，提高行走過程中機身穩定。仿真運行時，可以在MATLAB 中觀察并輸出仿真結果曲線，也可以在仿真結束后進入ADAMS 的后處理模塊觀察仿真結果。

機器人質心在X、Y、Z 三個方向的位移曲線分別如圖9—圖11 所示。X 方向為豎直方向，機器人質心在X 方向上的波動幅度為7 mm，機身質心離地高度為500 mm，則機器人質心豎直方向上的波動率為1.4%，運動較為平穩；Y 方向為機器人橫向方向，機器人質心的橫向波動幅度為22 mm，波動幅度較小；Z 方向為機器人的前進方向。從位移曲線可見，機器人在第1 s 內前進方向沒有移動，而豎直方向和橫向有輕微移動，這是因為在步態規劃中，前1 s 時間用于調整4 個足端的初始位置，所以會造成機身輕微的擺動。Z 方向位移曲線比較平滑，斜率基本保持不變，說明整個運動過程中機器人都能穩定行走。

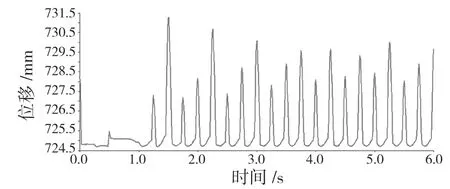
圖9 質心在X 方向的位移Fig.9 Displacement of the center of mass in X direction

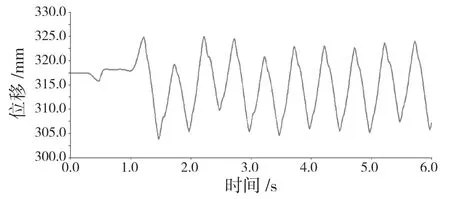
圖10 質心在Y 方向上的位移Fig.10 Displacement of the center of mass in Y direction

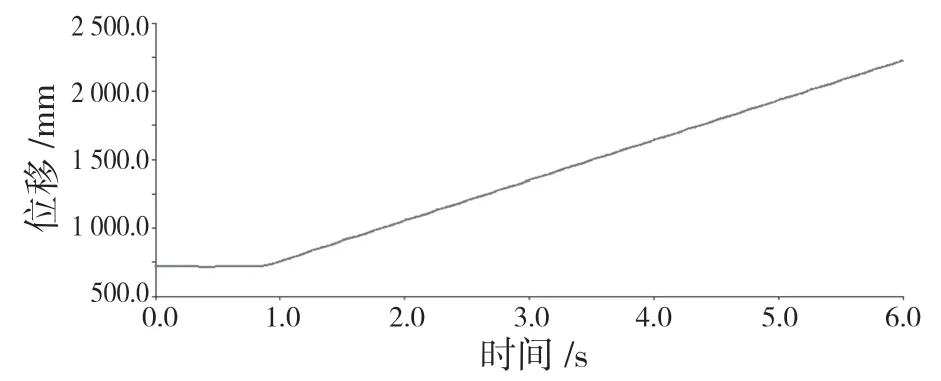
圖11 質心在Z 方向上的位移Fig.11 Displacement of the center of mass in Z direction

如圖12—圖14 分別為機器人在俯仰角、偏航角、橫滾角的變化曲線。機器人在整個仿真過程中，俯仰角變化幅度為1.26°，橫滾角變化幅度為2.46°，偏航角變化幅度為0.9°，3 個角度變化都比較小，說明在仿真過程中機器人機身擺動幅度較小并且保持在一個平穩狀態。

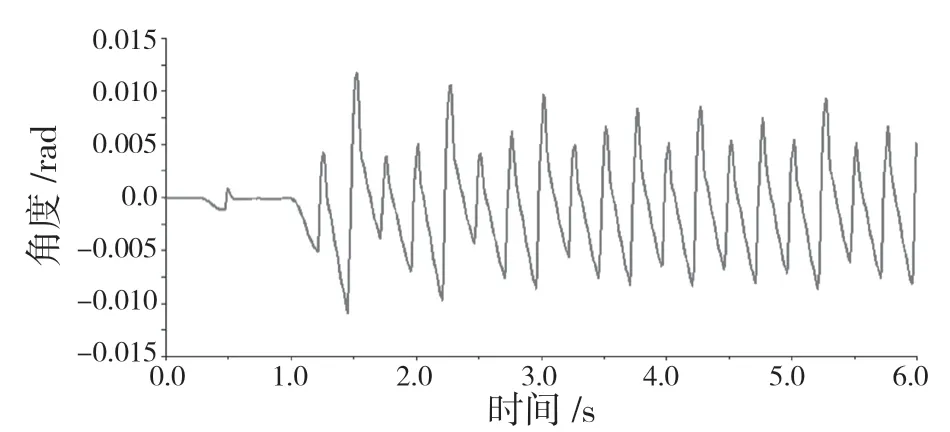
圖12 機器人俯仰角變化曲線Fig.12 Curve of robot pitch angle change

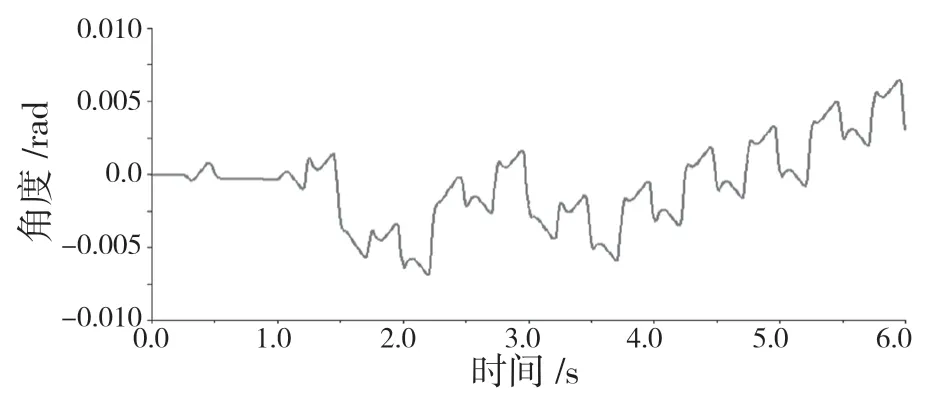
圖13 機器人偏航角變化曲線Fig.13 Curve of robot yaw angle change

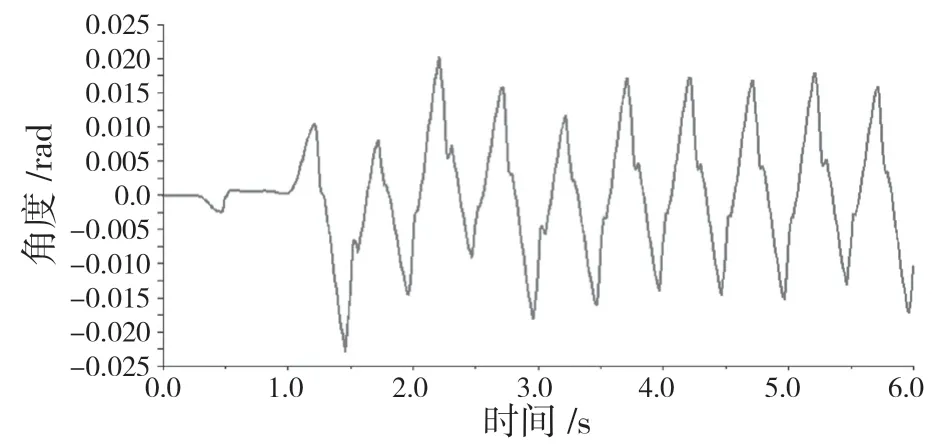
圖14 機器人橫滾角變化曲線Fig.14 Curve of robot roll angle change

從機器人偏航角的變化曲線可以看出，雖然在整個仿真的6 s 內，偏航角的變化幅度只有0.9°，但是隨著時間的推移，偏航角在不斷變大，這是每一個周期的偏航角偏差的疊加造成的。本文涉及到四足機器人姿態控制的內容，所以會產生這樣的現象，如果加上對機器人姿態的控制，可以將機器人的偏航角控制在一定范圍內。

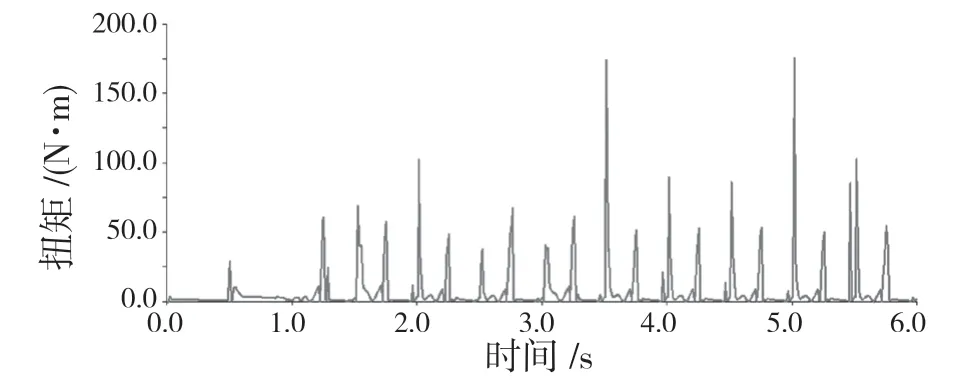
圖15 髖關節扭矩Fig.15 Torque of hip joint

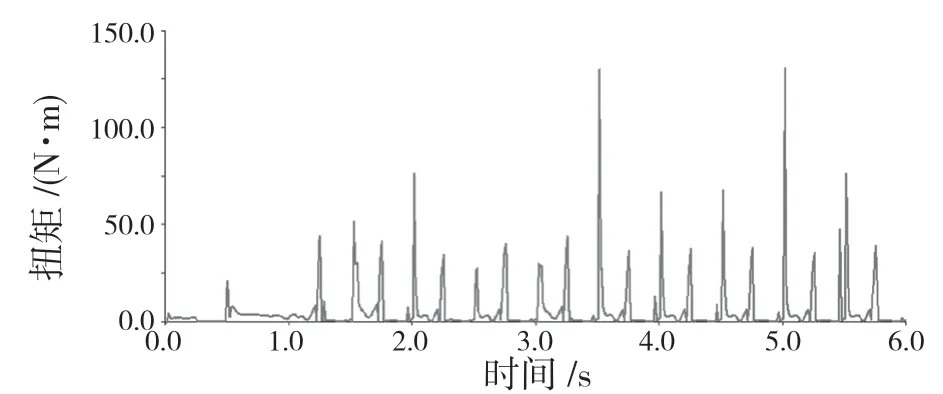
圖16 膝關節扭矩Fig.16 Torque of knee joint

圖15、圖16 所示為左前腿髖關節和膝關節的扭矩曲線。從圖中看到，關節扭矩有較大的波動，這是由足端與地面接觸時產生的較大沖擊導致的，如果在行走的基礎上加上腿部柔順性控制，可以很好地改善這種現象。從曲線中可以得到四足機器人左前腿髖關節最大扭矩為175 N·m,有效扭矩為45 N·m；左前腿膝關節最大扭矩為124.37 N·m，有效扭矩為 35 N·m。根據各關節的最大扭矩可以確定所用電機的轉矩，從而選擇電機的型號。

5 結語

本文設計了一款四足機器人結構，采用SolidWorks 建立機器人三維模型，并通過ADAMS、MATLAB 聯合仿真對四足機器人進行動力學仿真。分析機器人質心在不同方向上位移及機身姿態角的變化，可以看出機器人在整個運動過程中能實現穩定行走，驗證了該結構的可行性。同時得到機器人腿部關節的扭矩，為后續的物理樣機的研制提供了參考。通過此方法，可以方便地進行參數優化和性能預測，提早發現設計問題，大大提高設計效率，節省時間和經費。

雖然在整個仿真中機器人能實現穩定行走，但仍有不足之處，如：機器人的偏航角會隨著時間的推移越來越大；關節扭矩在足端觸地時會出現較大沖擊。這些問題都需要在后續的研究中改善相應的控制程序來解決。