超大型水中沉井下沉阻力研究
李嘉成 ,陳培帥 ,李德杰
(1.中交第二航務工程局有限公司,湖北 武漢 430040;2.長大橋梁建設施工技術交通行業重點實驗室,湖北 武漢 430040;3.交通運輸行業交通基礎設施智能制造技術研發中心,湖北 武漢 430040;4.中交公路長大橋建設國家工程研究中心有限公司,北京 100120)
0 引言
沉井具有水平和豎向承載力大、防撞性能好、抗震性能強等諸多優點[1-2],被廣泛應用在港口、橋梁、礦山及水利水電工程中。隨著我國橋梁建設向寬闊水域、外海發展,一座座跨江跨海特大型橋梁應運而生,超大型沉井基礎逐漸成為橋墩基礎的主要形式之一[3-7]。然而,特大型沉井基礎面臨著更大的水深以及更復雜的地質條件,下沉期間存在難沉、傾斜、翻砂突沉等一系列問題。為實現沉井可控下沉,準確確定下沉阻力至關重要。但是,對于土層的側摩阻力和地基承載力的取值,地勘資料一般僅給出其標準值,而標準值與極限值之間無換算關系,因此確定土層側摩阻力和地基承載力極限值往往依賴于經驗,缺乏理論支撐。
本文依托常泰長江大橋5 號墩沉井基礎,利用有限元極限分析方法和理論公式分別對地基極限承載力、極限側摩阻力進行計算,同時與CPTU靜力觸探試驗實測值進行了比較分析,以期獲取與工程實際更為接近的地基極限承載力和極限側摩阻力,從而實現沉井精準可控下沉。
1 工程概況
常泰過江通道位于泰州大橋與江陰大橋之間,距離泰州大橋約28.5 km,距離江陰大橋約30.2 km,主航道橋采用雙層斜拉橋,主塔為沉井基礎[8]。其中,5 號墩沉井基礎平面呈圓端形,立面為臺階形,其底面尺寸95.0 m×57.8 m(橫橋向×縱橋向),頂面尺寸 77.0 m×39.8 m(橫橋向×縱橋向),總高為72.0 m;該沉井為鋼殼混凝土結構,井壁厚2.0 m,隔墻厚度為1.4 m。沉井定位坐床后采用海床式靜力觸探系統(PeneVector-IIIA)在現場進行原位試驗,試驗計劃在9 個孔位進行靜探試驗,由于設備原因僅完成1 號、2 號、4 號和8 號4 個孔位試驗,沉井結構及靜力觸探孔位見圖1。
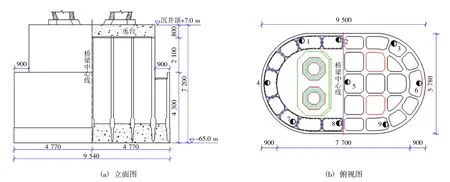
圖1 5 號墩沉井結構及靜力觸探孔位(mm)Fig.1 No.5 open caisson structure and static penetration hole location(mm)
2 沉井下沉阻力的研究
目前,超大型沉井下沉計算中土層參數取值依賴于地質勘探資料,但是地勘資料中地基承載力和側摩阻力建議值通常偏于保守,故沉井往往需要較大的下沉系數才能啟動下沉。為了精準指導沉井下沉,制定高效合理的取土下沉指令,關鍵在于獲取與工程實際更為接近的端阻力和側摩阻力。
2.1 計算參數
常泰長江大橋5 號墩沉井下沉深度范圍內(標高-75.0 m 以上)主要為砂層,其中有4 層粉質黏土層,根據地勘資料的各土層物理力學參數如表1 所示。
2.2 下沉阻力計算
沉井端阻力的計算可歸結為刃腳土體極限承載力的問題[9]。針對刃腳處土體的極限承載力,國內外許多學者進行理論研究,主要分為滑移線法、極限分析法、極限平衡法和有限元分析法[10]。其中,滑移線法和極限分析方法,推導過程復雜不易于工程設計人員掌握;極限平衡法相對簡單,許多參數以圖表的形式給出,便于在工程中推廣使用,但是該方法把刃腳簡化為條基,未能考慮刃腳楔形體對地基極限承載力的影響;另外,一些學者利用有限元軟件對刃腳處地基承載力進行計算,但是有限元計算中地基破壞沒有定量的判斷標準。近年來,有限元極限分析方法應運而生,它能通過降低土體強度或者增加荷載直接算得巖土工程的滑動面,進而判斷地基、邊坡及隧道的穩定性[11]。
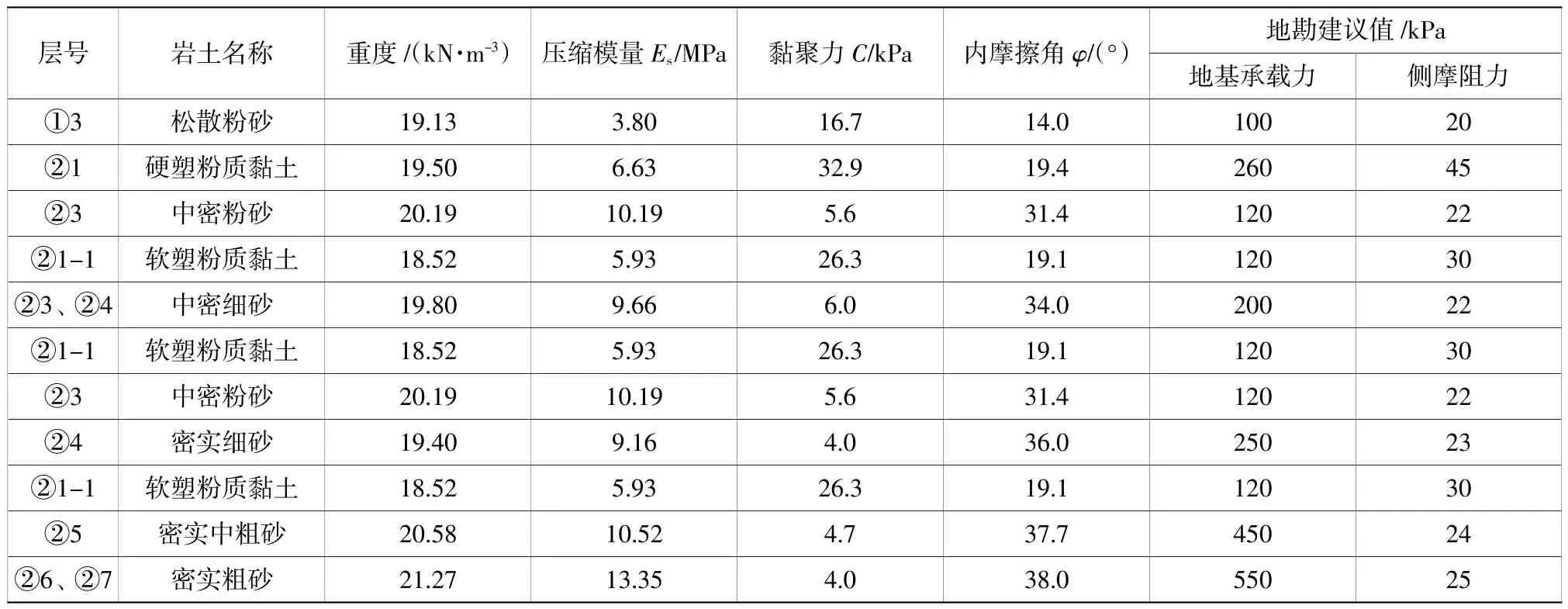
表1 5 號墩沉井土層物理力學指標Table 1 Soil physico-mechanical index of the No.5 open caisson
鑒于此,本文采用有限元極限分析方法計算刃腳處土體的極限承載力。首先,建立二維極限分析有限元計算模型,土體采用M-C 本構模型,其物理力學參數見表1;沉井刃腳彈性模量為30 GPa,泊松比0.25;刃腳采用局部模型,其寬度為B=2 m,高度為2.5B=5 m,刃腳切削角度為45°;土體水平方向向刃腳外每邊延伸長度為20 m、深度方向為20 m,其左右兩側約束水平方向位移,土體底部約束水平及豎向位移,沉壁兩側約束水平位移;模型中利用在沉井外側施加均布荷載等效為外側覆土來考慮覆土深度。模型中通過在刃腳頂部施加荷載,該荷載從初始值逐漸增加到土體達到極限破壞,土體極限破壞時對應的荷載即為極限荷載,計算模型、邊界條件及網格劃分如圖2 所示。
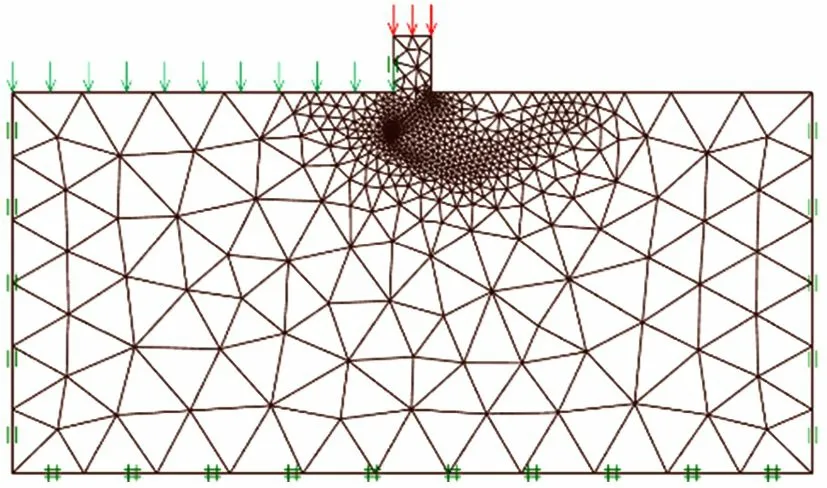
圖2 計算模型及網格劃分Fig.2 Calculation model and meshing
圖3 為刃腳處地基土體破壞時塑性區云圖,由圖可知刃腳傾斜面側土體出現整體滑移即發生整體剪切破壞,其剪切破壞面是從刃腳踏面處開始一直延伸至土體頂部,利用該方法依次計算各土層地基極限承載力。
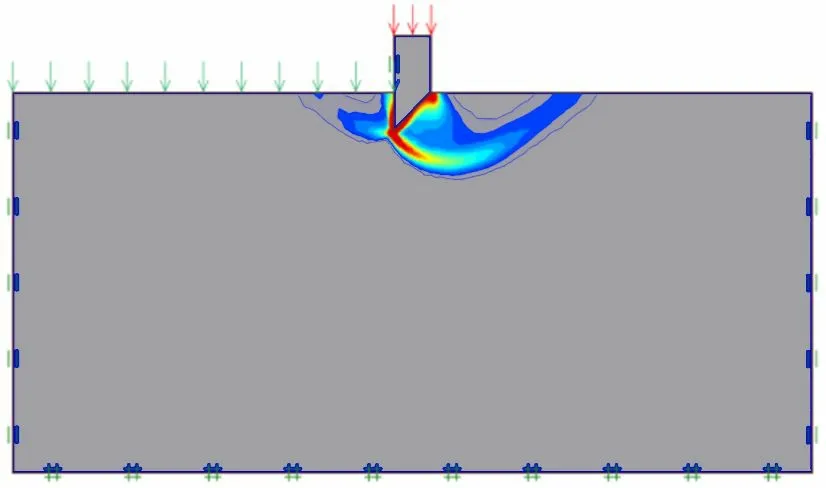
圖3 刃腳切削土體極限破壞Fig.3 The ultimate failure mode of cutting edge in cutting soil
隨著沉井下沉深度的增加側壁摩阻力的占比越來越大,因此側阻也是下沉阻力的重要組成部分。邁耶霍夫(1976 年)[12]認為土體與打入樁之間極限側摩阻力由有效應力強度參數控制,由式(1)表示:

式中:σv為樁埋深范圍內的平均豎向應力;c 為土體黏聚力;φ為土體內摩擦角;k 為土體的側壓力系數,取k=1-sin φ。沉井下沉過程與打入樁相似,故參考打入樁極限側摩阻力計算公式計算各土層側摩阻力。理論計算得到的極限地基承載力和極限側摩阻力結果見表2 所示。

表2 理論計算與靜力觸探試驗推算結果Table 2 Theoretical calculations and static cone penetration test results
3 靜力觸探數據分析
雙橋靜力觸探試驗可獲取錐尖阻力qc、側壁摩阻力qs,對4 個孔中各土層的錐尖阻力和側摩阻力求取平均值(見表2),然后根據相關規程中總結的經驗公式可對各土層的地基極限承載力和極限側摩阻力進行推算。
針對極限承載力,可參考TB 10018—2018《鐵路工程地質原位測試規程》[13]給出的天然地基極限承載力(Pu)計算公式,各土層極限承載力經驗公式見表3 所示。
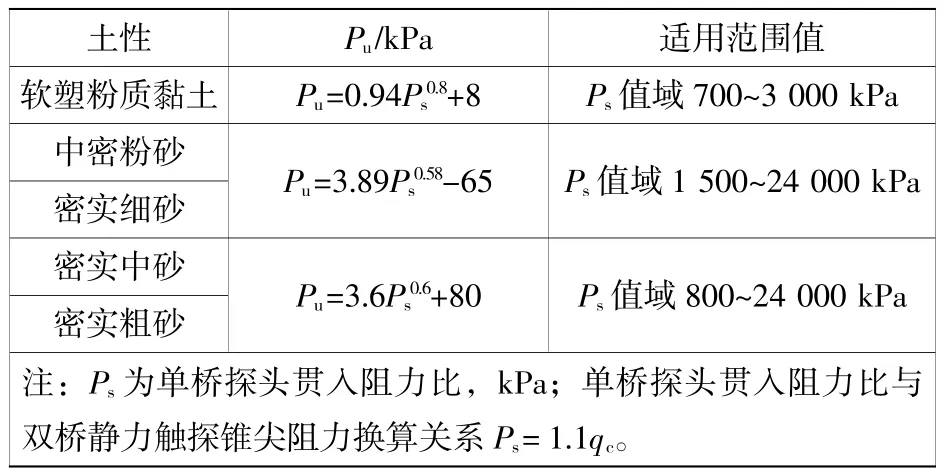
表3 天然地基極限承載力(Pu)算式Table 3 Formula for ultimate bearing capacity(Pu)of natural foundation
對于極限側摩阻力,雙橋靜力觸探對土層側摩阻力進行了測試,但是真實極限側摩阻力的取值并不能直接采用測試的側阻力結果。其原因是靜力觸探探頭貫入過程中產生超孔隙水壓力且超孔隙水壓力分布不均,摩擦筒底部的超孔隙水壓力大于摩擦筒頂部的超孔隙水壓力,從而超孔隙水壓力和摩擦筒側壁土體一起阻止探頭貫入,故雙橋探頭測試的側摩阻力大于真實側摩阻力[14-15]。文獻[16]針對側阻真實值與側阻實測值進行了試驗研究,并提出側阻真實值約為側阻實測值的37.8%。本文采用該比值對側阻實測值進行修正。將錐尖阻力qc、側壁摩阻力qs代入公式,分別計算出各土層的地基極限承載力和極限側阻力推算值,計算結果如表2 所示。
4 結果對比分析
為了驗證結果的合理性,將理論計算結果與靜力觸探試驗推算值進行比較分析。有限元及理論計算值與靜力觸探值的對比如表2 所示。由表可知,理論計算結果與靜力觸探試驗推算結果兩者基本吻合。靜力觸探試驗推算地基極限承載力與計算的地基極限承載力相對偏差均在15%范圍內,靜力觸探試驗推算側阻力與計算側阻力相對偏差在20%范圍內,計算誤差滿足工程需求,表明了計算結果的合理性。但是,靜力觸探的地基極限承載力基本大于理論計算值,因為刃腳楔形體有一定的切削角度便于沉井切土下沉,且由極限分析計算結果可知刃腳處土體破壞時僅斜面側土體發生整體剪切破壞,而條形基礎在其左右兩側均發生整體剪切破壞,抗力相對較大,故靜力觸探試驗參數套用條形基礎的極限承載力經驗公式的計算值偏大。
5 結語
1)有限元極限分析方法計算地基極限承載力和理論計算的極限側摩阻力與靜力觸探試驗推算值比較接近,初步驗證了地基極限承載力和極限側摩阻力計算方法的合理性,為沉井下沉阻力計算提供思路。
2)極限破壞時,沉井刃腳僅在斜面側產生貫通滑動面,而條形基礎在其左右兩側均產生貫通滑動面,故靜力觸探套用條形基礎的極限承載力經驗公式計算值較有限元極限分析方法的計算值偏大。
3) 本文為沉井下沉阻力計算提供了一定依據,但是實際施工過程中地質情況復雜,需在沉井下沉過程中,加強對土層參數的反演計算,同時根據反演結果及時調整開挖下沉工藝。

