鉸接式轉向架構架疲勞強度算法優化研究

（北京軌道交通技術裝備集團有限公司，北京 100071）

1 研究背景

車輛轉向架的構架疲勞強度分析是轉向架構架設計的關鍵環節，對轉向架運用過程的安全性有重大影響[1-2]，國內外也有很多與之相關的標準和研究[3-6]。DVS 1612為德國《鐵路車輛結構鋼焊接接頭設計和疲勞強度評估》標準，其中對轉向架構架常用的焊接接頭形式做了較為詳細的規定，十分適合轉向架構架的焊接疲勞強度設計，因而運用得越來越廣泛[7]。國內也有較多學者和工程師對DVS 1612標準展開了研究[8-11]。

為得到符合DVS 1612標準的應力分布[12-13]，需獲得沿焊縫方向、垂直于焊縫方向的正應力和沿焊縫方向的剪應力，而一般有限元軟件所得到的應力往往遵循全局坐標系或者是主應力和最大剪應力，必須對應力計算結果進行坐標變換。由于構架上焊縫數目較多，在空間中的角度分布也各異，因此這一過程往往十分復雜。本文直接利用焊縫名義應力的最大主應力和剪應力分量，基于DVS 1612標準，提出一種疲勞評估修正算法，并針對某轉向架構架進行焊縫疲勞強度評估。

2 DVS 1612標準算法

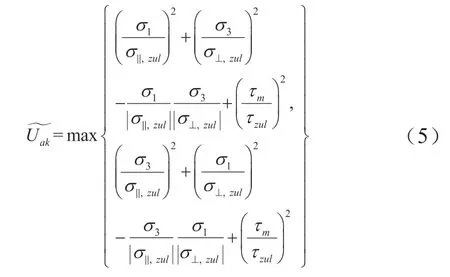
根據DVS 1612標準，焊縫疲勞評估需要先得到基于焊縫方向的3種應力：平行于焊縫的正應力σ∥，垂直于焊縫的正應力σ⊥以及平行于焊縫的剪應力τ。而根據材料屬性、應力比和接頭形式，可以得到焊縫的3種許用應力：平行于焊縫的許用正應力，垂直于焊縫的許用正應力以及平行于焊縫的許用剪應力τzul。為了滿足疲勞壽命，焊縫名義應力需要滿足以下條件：

針對某轉向架構架，對實際應用中受載荷較大的制動座、側梁等部位進行焊縫疲勞強度評估。構架所用材料為S355鋼[9]，構架網格模型如圖1所示。

圖1 構架網格模型

將有限元計算結果變換為焊縫局部坐標系的應力分布后，得到σ∥、σ⊥、τ。制動座和側梁上2條承受載荷較大的焊縫（焊縫1和焊縫2）的利用度沿焊縫長度的分布如圖2和圖3所示。

由圖可以看出，制動座、側梁的焊縫強度單向應力利用度小于1，綜合利用度均小于1.1，滿足疲勞使用壽命要求。

3 基于主應力和最大剪應力的疲勞評估修正算法

圖2 焊縫1利用度沿焊縫長度分布

圖3 焊縫2利用度沿焊縫長度分布

任意結構中某一點的應力均可以用其3個方向的主應力狀態表達，將3個方向的主應力分別記為σ1、σ2、σ3，三者相互正交[14]。由于構架往往由鋼板拼焊而成，焊縫處的應力基本為平面應力狀態，因此鋼板中某一點的主應力滿足以下條件：垂直于鋼板的應力|σ2|≈0，σ1、σ3處于板材平面內且正交分布。

某構架制動座焊縫處的主應力流線如圖4所示，可以看到，主應力流線均分布于平面內，并且方向與焊縫走向基本一致；其主應力σ1、σ2、σ3沿焊縫長度方向應力分布如圖5所示，可見垂直于鋼板的應力σ2基本為0。

由于主應力方向與焊縫走向具有一定程度的重合，因此，可以將主應力σ1和σ3作為σ||和σ⊥的估計值，并用最大剪應力τ m替代平行于焊縫的剪應力τ[14]。主應力和最大剪應力狀態可以直接從商業有限元軟件中獲取，避免了將全局坐標系下的應力轉化為沿焊縫不斷變化的局部坐標系下的應力，簡化了計算過程。

根據DVS 1612標準，采用主應力和最大剪應力的疲勞評估方法對構架制動座、側梁等危險焊縫進行疲勞強度評估，將式（4）轉化為：

圖4 制動座焊縫處主應力流線

圖5 主應力沿焊縫長度方向應力分布

4 修正算法與標準算法和商用軟件算法對比

4.1 計算精度對比

采用主應力和最大剪應力進行焊縫疲勞強度評估會帶來誤差[15]。下面分析該修正算法產生的精度影響。

設主應力方向與焊縫方向夾角為α，則主應力σ1、σ3和最大剪應力τ m與標準中的σ||、σ⊥、τ存在如下關系[14]：

記利用度函數：

圖6 相對誤差與夾角α 的變化關系

針對某構架承受載荷較大的2條焊縫（焊縫3和焊縫 4），分別采用 DVS 1612標準算法、商用軟件LIMIT算法和本文修正算法計算焊縫疲勞強度利用度，結果如圖7和圖8所示。

由圖可知，商用軟件LIMIT算法所得到數值最大，結果最為保守（這是由于軟件直接提取距離焊縫最近處的位移和應力），標準算法數值最小，本文提出的算法介于兩者之間，既充分考慮了利用度，又不會造成估計不足的風險。

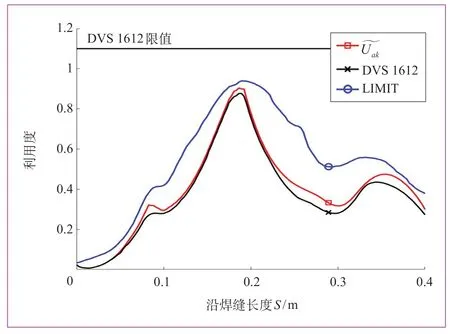
圖7 不同算法下焊縫3的利用度對比

圖8 不同算法下焊縫4的利用度對比

4.2 算法復雜度對比

由于商用軟件LIMIT算法需要根據節點位移數據計算應力，而DVS 1612標準算法需要將全局坐標下的應力轉化為沿焊縫方向的正應力、垂直于焊縫方向的正應力和沿焊縫方向的剪應力，因此二者均需花費較長時間[15]。為對比上文介紹的3種算法所需要的計算時間，采用復雜度的概念進行分析。本文的復雜度是指將算法編制為可執行程序后運行所需要的時間資源。

4.2.1 商用軟件 LIMIT算法

根據LIMIT軟件所采用的“sensor單元”方法[16]，需進行以下步驟。

第一步：求sensor單元的位移，需進行42次加減法和42次乘法。

第二步：求sensor單元的應變和應力，需進行241次加減法和206次乘除法。

第三步：進行綜合利用度計算，共需要4次加減法和12次乘除法計算。

由于加減法的復雜度為O（n），乘除法的復雜度為O（nlogn），因此對包含n個節點的焊縫，共需進行287n+260nlogn次計算[15]。

4.2.2 DVS 1612標準算法

針對DVS 1612標準算法需要進行以下步驟[16-19]。

第一步：求焊縫節點的局部坐標系的方向余弦（x軸沿焊縫方向），共需要進行107次加減法計算和63次乘除法計算。

第二步：求在局部坐標系下的方向應力，共需要進行36次加法和54次乘法。

第三步：進行綜合利用度計算，共需要4次加減法和12次乘除法計算。

對包含n個節點的焊縫，共需要進行147n+129nlogn次計算。

4.2.3 修正算法

本文提出的修正算法只需要進行綜合利用度計算，步驟如下。

第一步：用σ1替代σ||、σ2替代σ⊥，用τm替代τ，進行綜合利用度計算，共需要4次加減法和12次乘除法計算。

第二步：交換σ1和σ2的位置，再次進行綜合利用度計算，共需要4次加減法和12次乘除法計算。

第三步：比較第一步和第二步所得結果大小，并取較大值。

因此，對1個節點需進行8次加減法和24次乘除法計算，對包含n個節點的焊縫共需進行8n+24nlogn次計算。

圖9對三者的計算復雜度進行了對比，可見本文提出的利用度修正算法的計算復雜度遠低于另外2種方法。一個構架上焊縫節點數目達到數十萬個，因此采用本文算法可以節省較多時間。

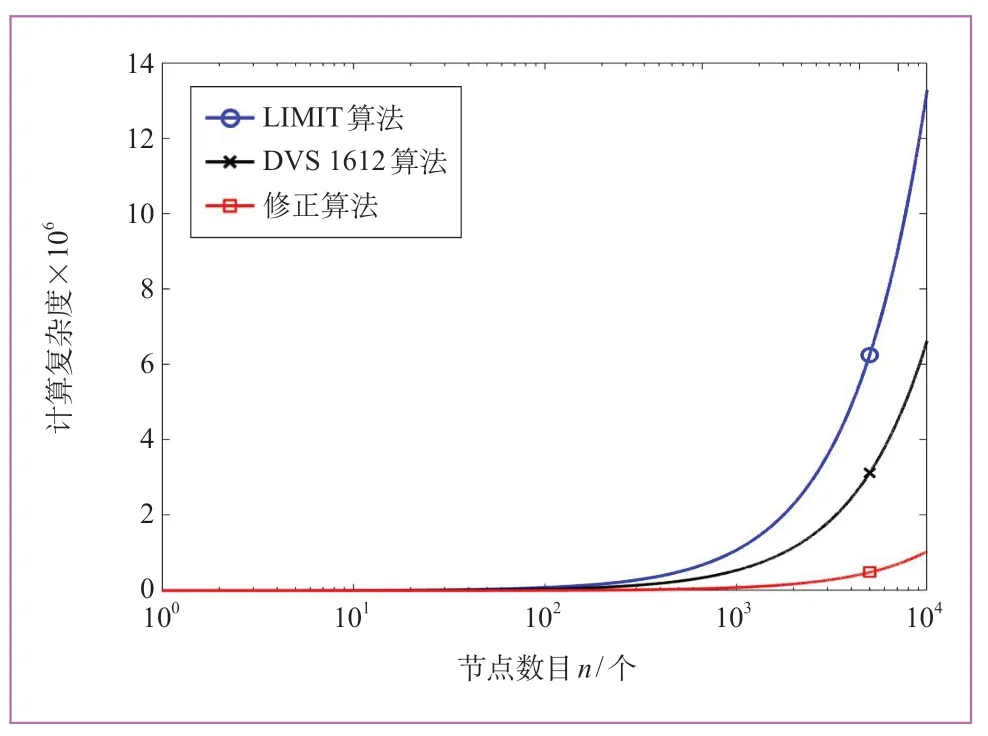
圖9 不同算法計算復雜度對比

5 結論

本文基于DVS 1612標準多軸應力狀態下的綜合利用度，根據構架焊接結構特點，提出一種利用主應力和最大剪應力進行焊縫疲勞強度評估的修正算法，并對某構架關鍵部位進行了疲勞強度評估。通過對比DVS 1612標準算法、商用軟件LIMIT算法和修正算法的精確度和復雜度，得出以下結論。

（1）由于焊縫處主應力方向與焊縫方向存在很高的一致性，因此采用基于主應力和最大剪應力的方法進行焊縫疲勞強度評估具有較高準確度。

（2）修正后的算法相比標準算法更加保守，但比商業軟件利用率更高，滿足工程實踐的需求。

（3）修正后的算法復雜度相比商用軟件算法和標準算法顯著降低，提高了運算效率，具有較大的工程應用意義。