軟土地區地鐵環境振動對精密儀器的影響研究

（中鐵工程設計咨詢集團有限公司，北京 100055）

1 引言

城市軌道交通具有運量大、速度快、安全性好、準點率高等諸多優點，但地鐵運營中出現了沿線工廠、科研機構內精密儀器運行受影響，以及周邊建筑結構內二次噪聲超標等環境振動問題。

軟土地區含水率大、壓縮性高、剪切波速小，地鐵列車動力作用對周邊環境振動影響大，且在中低頻范圍內振動增加明顯。因此，環境振動對精密儀器的影響愈發引起人們的重視，諸多專家學者針對這一問題進行了大量測試與研究，包括北京地鐵4號線列車運行引起的振動對北京大學物理樓內精密儀器的影響，北京地鐵16號線規劃通過北京大學西門對200 m外的實驗樓內精密儀器的影響，北京地鐵15號線規劃下穿清華大學對校內200余臺精密儀器的影響，北京地鐵10號線近距離經過中國空間技術研究院等。以上工程案例均存在環境振動對精密儀器的影響問題，且難以解決。目前降低環境振動對精密儀器的影響措施主要為被動隔振措施，但效果十分有限，故研究地鐵線路周邊精密儀器合理的放置距離十分必要。

蘇州地鐵6號線蘇州大學站—徐家浜站區段鄰近蘇州大學某實驗樓，實驗樓中多臺精密儀器受到地鐵振動的影響。蘇州地鐵6號線位于軟土地區，由其導致的周邊建筑結構振動及其衰減特性尚不明確，需對蘇州地鐵6號線對該建筑（實驗樓）內精密儀器的影響程度進行模擬計算評估。

2 環境振動分析預測有限元模型

本文結合蘇州地鐵6號線蘇州大學站—徐家浜站區段減振軌道工程案例，基于有限元方法建立包含車輛、軌道、隧道、土體、建筑的動力學有限元模型。蘇州地鐵6號線采用地鐵B型車，列車運行速度60 km/h，鋼彈簧浮置板軌道板長6 m，鋼彈簧與扣件采用彈簧單元模擬，軌道結構如圖1所示。

有限元模型中軌面至地表距離20 m，在模型中分別考慮隧道中心線距建筑物（內有精密儀器）20 m、50 m、100 m 3種工況。模型隧道為單洞單線隧道，隧道直徑6 m，縱向長96 m。隧道襯砌為C50混凝土。建筑物為鋼混結構，共4層（含地下一層），建筑物梁、柱、墻、板均采用C30混凝土，建筑物與周圍土體共結點綁定。地鐵隧道-建筑物空間位置關系如圖2所示。

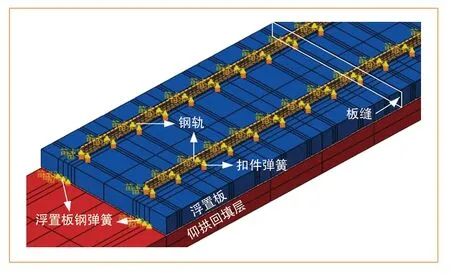
圖1 軌道結構示意圖

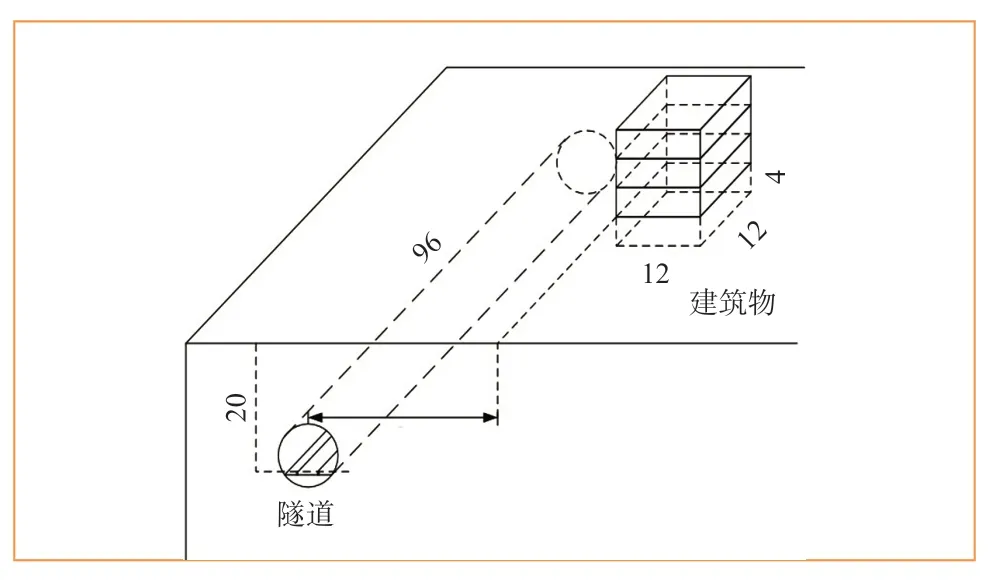
圖2 隧道-建筑物空間位置關系示意圖（單位：m）

研究表明交通荷載引起的土體動應變在10-5以下，在仿真中可忽略土體的塑性變形；有限元分析中，將隧道和土層之間的連接按照共用節點的方式處理，土體結構采用實體單元模擬，參數根據地勘報告取值。

本文采用三維黏彈性人工邊界作為邊界條件，以減少邊界反射帶來的影響。三維黏彈性人工邊界的等效物理系統的切向、法向彈簧系數和切向、法向阻尼系數分別為

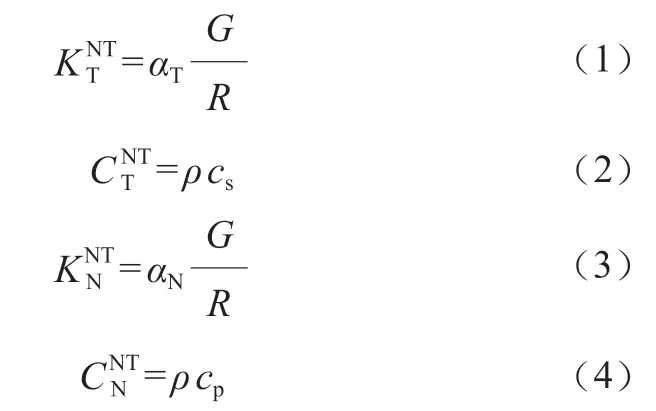
式（1）～式（4）中，R為振源與人工邊界間的距離；G為介質剪切模量；ρ為土體密度；cs為剪切波速；cp為壓縮波速；αT和αN分別為切向和法向黏彈性人工邊界參數，其取值范圍分別為0.5～1.0和1.0～2.0，結合文獻[18]，本文取αT=0.67，αN=1.33。

圖3 環境振動分析預測模型

本文應用ABAQUS顯式算法，建立環境振動分析預測模型如圖3所示，模型共包含1 386 000個網格單元，采用美國六級譜作為輪軌激勵。

3 浮置板振動模態分析

振動模態是彈性結構固有的、整體的特性，了解結構的固有屬性是進行結構振動特性分析的重要前提。當外界激勵頻率與結構模態相近時，結構的振動響應將顯著增大。本文基于有限元軟件ABAQUS線性攝動分析，采用子空間迭代法分析進行鋼彈簧浮置板模態分析，得到的鋼彈簧浮置板典型模態頻率如圖4所示，其中前2階4.86 Hz與12.58 Hz模態為浮置板縱向上的轉動，此為浮置短板的特征模態，亦為鋼彈簧浮置板主要的運動模態，其后為1階彎曲，再之后為復雜的扭轉與高階彎曲模態。由此可知，鋼彈簧浮置板的主要模態頻率較低，在外界荷載激勵作用下，鋼彈簧浮置板將難以隔絕低頻振動。

4 動力學仿真分析

4.1 軌道-隧道結構動力響應

為分析振源位置的振動響應特性，選取鋼軌、軌道板、隧道壁（高1.2 m處）位置上各1點進行振動加速度時程與振動加速度1/3倍頻程分析，所得結果如圖 5、圖6所示。由圖5可知，鋼軌峰值加速度為120 m/s2，軌道板峰值加速度為13 m/s2，隧道壁振動加速度峰值為0.05 m/s2；由圖6可知，在12.5 Hz附近出現明顯的峰值，分析原因與浮置板主要的運動模態相關。

4.2 地面自由場振動衰減分析

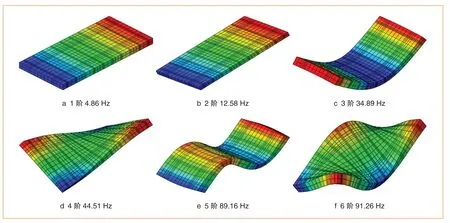
圖4 鋼彈簧浮置板典型模態頻率

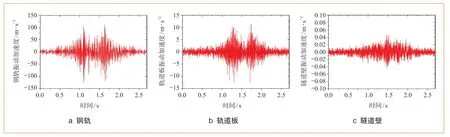
圖5 鋼軌、軌道板、隧道壁振動加速度時程曲線

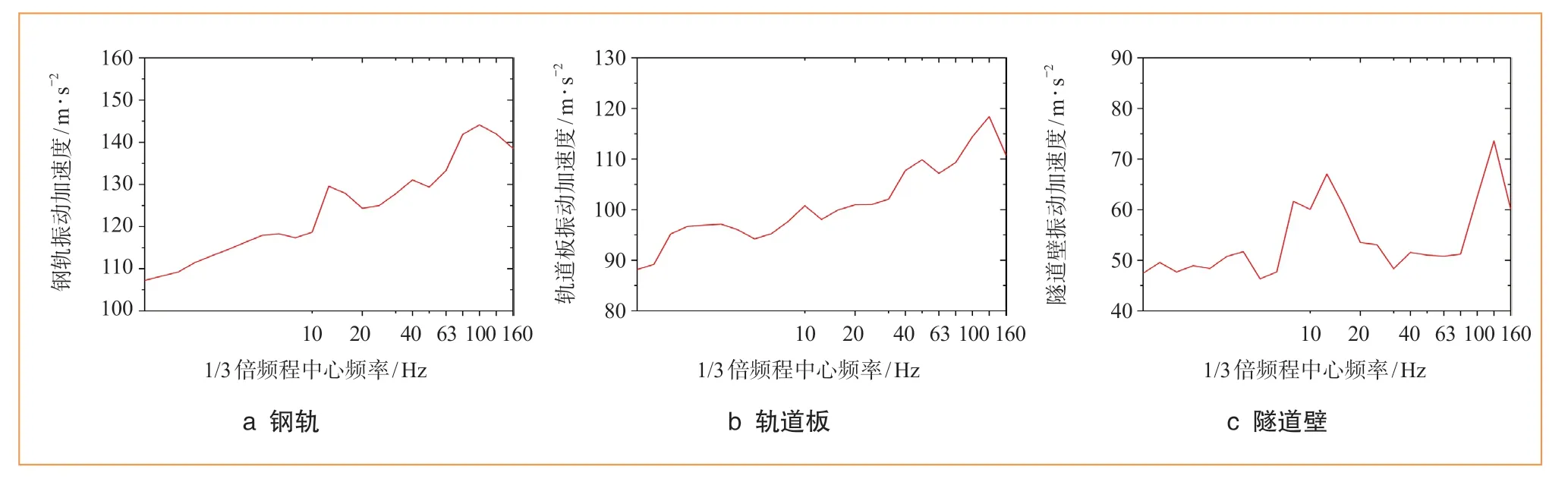
圖6 鋼軌、軌道板、隧道壁振動加速度1/3倍頻程曲線

為研究列車運行振動引起地表自由場振動衰減規律，在距隧道中心線0～115 m的范圍內選取了一些典型測點，并選擇對遠場影響較大的垂向振動加速度作為研究指標，計算得到距隧道中心線不同距離與垂向振動加速度關系曲線如圖7所示。由圖7可知，在15 m左右出現明顯的“振動放大區”，該位置至隧道中心線的距離與地鐵隧道埋深相近；在80～90 m附近出現第2個放大區；隨著距離的增加，整體上振動加速度呈減小趨勢，最大振動加速度位于距隧道中心線15 m左右位置。

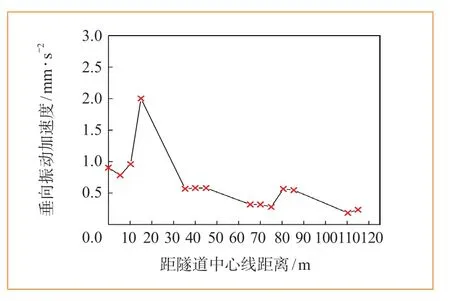
圖7 地表垂向振動加速度與隧道中心線距離關系曲線

5 建筑結構室內振動響應與影響評估

本文工程實例中，實驗樓內放置有需要滿足VC標準（Generic Vibration Criteria）中VC-D級振動標準的精密儀器。VC標準制定的目的是給出特定工藝和設備振動標準的下限，VC標準以1組1/3倍頻帶速度譜的形式標記振動標準曲線（VC-A到VC-G），VC-D級標準要求速度均方根值小于6.25 μm/s。計算得到的不同樓層、不同振源距離位置處的速度均方值1/3倍頻程曲線如圖8、圖9所示（圖中紅線表示VC-D振動標準限值），由圖8可知，所有位置速度均方值1/3倍頻程關系曲線均在4 Hz、12.5 Hz處存在速度均方根值峰值，對比分析圖8、圖9不同振源距離、不同樓層速度均方值1/3倍頻程曲線可知，距振源20 m、50 m的建筑物內的振動速度均方值均超過精密儀器對環境振動的要求限值，距振源100 m的建筑物內仍有環境振動超限的風險。

6 結論及建議

本文通過建立軟土地區環境振動分析預測模型，對蘇州大學某實驗樓受蘇州地鐵6號線環境振動影響問題進行分析計算，得到主要結論如下：

（1）地鐵環境振動對精密儀器的影響頻率范圍主要是12.5 Hz左右的低頻振動；

（2）地鐵環境振動在自由場地的傳播中存在部分“振動放大區”，本文中在距隧道中心線100 m的計算范圍內，存在15 m和80 m 2個較為明顯的振動放大區；

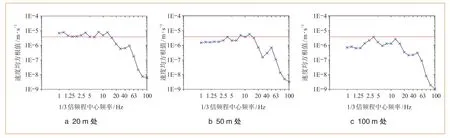
圖8 負一層地板速度均方值1/3倍頻程曲線

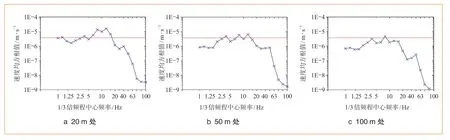
圖9 地面地板速度均方值1/3倍頻程曲線

（3）本文中距振源20 m、50 m、100 m 3種工況中，距振源20 m、50 m的建筑物內振動超過精密儀器對環境振動的要求限值，距振源100 m的建筑物內仍有振動超限的風險；

（4）軟土地區距離地鐵線路100 m的范圍內不應放置精密儀器。