基于ESO的運載火箭姿控噴管故障辨識設計及實現

潘 豪，王光輝，邵夢晗，胡煜榮，羅宛臻

（北京航天自動控制研究所，北京，100854）

0 引 言

運載火箭發射技術難度大，系統復雜，是一項高風險的系統工程。隨著中國不斷深入開展月球探測、火星探測等重大航天工程，對運載火箭的穩定性、可靠性以及自主運行能力的要求都明顯提升。在火箭各大分系統中，運載火箭動力分系統故障導致任務失敗的案例最常發生[1]。

姿控噴管作為動力系統的一種，主要用于實現運載火箭在停泊軌道滑行時的姿態控制、主發動機工作段的推進劑沉底管理等過程中[2]，其故障模式種類繁多，一旦出現故障，就會導致火箭的控制能力受損。歷史上曾經出現因人為因素，導致姿控噴管出現極性故障，致使任務失敗的案例。這就要求控制系統具備自適應能力與自主性，在故障情況下通過算法設計更改控制策略，實現故障后的控制重構，最大限度地挽救發射任務。

基于噴管控制的繞心運動，其姿控系統由導航裝置、計算裝置、執行裝置以及信息傳遞裝置組成。當計算軟件、線路連接、姿控噴管[3]或其它系統出現故障（如結構安裝、泄露等）時，均會引起姿控系統工作異常，若能夠及時進行控制效果辨識，對非致命性故障進行快速控制重構，則仍可保證姿控系統正常工作。大多數計算軟件錯誤、線路連接錯誤均可通過地面測試發現，但噴管故障不容易通過測試發現。

為充分吸取歷史發射失敗的教訓，發揮控制系統作用，解決姿控發動機（噴管）等姿控系統故障導致的飛行失利問題，本文研究設計了基于噴管故障的運載火箭姿態控制故障辨識方法，根據擴張狀態觀測器（extended state observer，ESO）實時辨識的控制效果進行姿控噴管故障識別和極性糾正，進一步提升運載火箭自主適應能力和智能化水平。

1 姿控噴管配置與火箭動力學模型

1.1 姿控噴管配置

本文研究對象為帶推進劑晃動的軸對稱運載火箭，其典型姿控噴管配置如圖1所示，共用8臺姿控噴管進行繞心運動控制。定義消除箭體正姿態偏差的噴管為正向噴管，反之為負向噴管，即1φ、ψ2、γ2、4γ為正噴管，ψ1、φ2、γ1、γ3為負噴管。典型姿控噴管控制配置如表1所示。

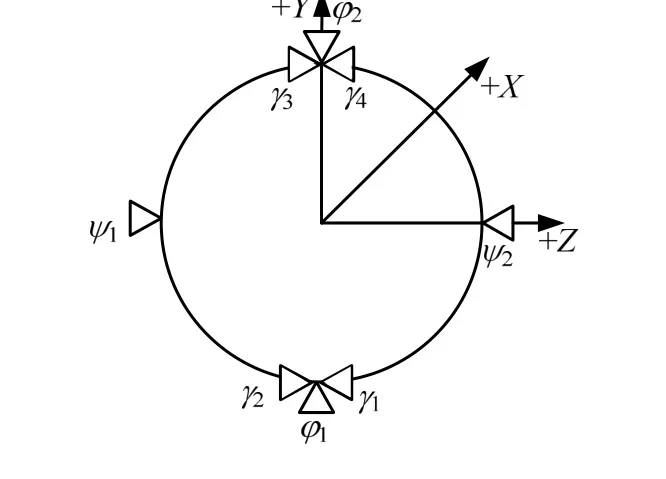
圖1 典型姿控噴管布局示意Fig.1 Layout of Typical Attitude Control Nozzle

姿控噴管特性用一階環節與延時環節模擬[1]，用式（1）表示，其中延時環節的延時時間和一階環節的時間常數滿足熱啟動加速性和熱關閉減速性的要求。

文中的姿控噴管為具有繼電特性的非線性規律[3]，即當輸入超過一定門限時噴管開啟，小于一定門限時噴管關閉，開啟和關閉過程服從式（1）中的延時特性和動態特性。姿控噴管的非線性規律如圖2所示。

圖2 姿控噴管非線性規律示意Fig.2 Nonlinear Law of Attitude Control

1.2 運載火箭動力學模型

以常規軸對稱運載火箭為研究對象，運載火箭僅采用姿控噴管進行繞心運動控制，考慮在大氣層外飛行，忽略大氣影響。采用箭體坐標系描述力矩平衡方程，運載火箭的動力學方程如下[4]。其中式（3）為推進劑晃動方程，對繞心運動方程的作用是產生晃動干擾力矩，即式（2）中偏航和俯仰通道動力學方程中的

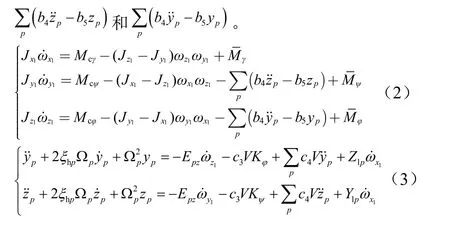
式中Mcγ，Mcψ，Mcφ為3個通道的控制力矩；為干擾力矩；為箭體三軸轉動慣量；為箭體三軸角速度。

2 自抗擾估計原理

自抗擾控制是在借鑒PID思想的基礎上發展起來的一種新型控制方法，采用了“基于誤差消除誤差”的控制策略[5]。自抗擾的思想是主動從被控對象的輸入輸出信號中把擾動的信息觀測出來，以觀測的擾動信息為依據，在擾動影響系統時設計一定的控制形式把擾動的影響消除掉[6]。未知擾動的實時跟蹤估計及補償是自抗擾控制最重要的優點，它根據對象的輸入輸出信息建立ESO，估計作用于對象的擾動的實時作用量，從而為解決大范圍不確定性提供了途徑[7]。

常規自抗擾控制器結構如圖3所示。

圖3 自抗擾控制器結構框圖Fig.3 Structure Block Diagram of Active Disturbance Rejection Controller

根據圖3可知，控制器設計分為如下幾個步驟：

a）安排過渡過程，并提取微分信號；

b）設計ESO，估計狀態及總干擾；

c）設計控制器，補償總干擾并設計誤差反饋控制律。

根據被控對象特點，以擴張狀態觀測器為主要手段，進行噴管自適應故障辨識與重構設計，利用ESO估計箭體所受的總擾動力矩，即火箭角加速度的估計值，作為故障識別和極性糾正的依據。

3 噴管自適應故障辨識與極性糾正設計

3.1 故障辨識和極性糾正策略

為了觀測器設計的便利，首先對運動模型式（4）進行形式上的變換。姿態控制的對象為箭體系姿態和箭體角速度，式（4）易變換為式（5）形式：

式中

ω×為ω的斜對稱矩陣。

進一步可令X1=ω，則式（5）可改寫為式（6）：

根據模型式（6）設計觀測器形式為

式中Z1為角速度估計值；E1為估計誤差，E1=Z1-X1；β1，β2均為擴張狀態觀測器反饋增益；Z2為角加速度估計值，也即此時箭體所受的“總和干擾”（包括所受的控制力矩和干擾力矩）。

設f為根據各通道姿控噴管控制能力預設的三通道極性故障判別閾值，令下面以滾動通道為例說明噴管故障判別和極性糾正策略。

當發送至姿控噴管的指令為正開狀態時，即γ2、γ4#噴管開啟，產生負向的控制力矩，應消除正向偏差。若有則可初步判別滾動噴管極性故障，需要進一步驗證，即對γ2、γ4#噴管發送強制關閉指令，同時開啟γ1、γ3#噴管，若有成立，則說明極性更改正確，之后需要噴管正開的時候發送指令至γ1、γ3#噴管。

當發送至姿控噴管的指令為處于負開狀態時，即需要γ1、γ3#噴管開啟，產生正向的控制力矩，應消除負向偏差。若有則可初步判別滾動噴管極性故障，需要進一步驗證，即對γ1、γ3#噴管發送強制關閉指令，同時開啟γ2、γ4#噴管，若有成立，則說明極性更改正確，之后需要噴管負開的時候發送指令至γ2、γ4#噴管。

俯仰、偏航通道具有相同的判別和糾正策略。

本文所提出的故障辨識和極性糾正策略簡單易于工程實現。故障辨識的核心采用擴張狀態觀測器進行角加速度信息的估計，根據飛行狀態信息估計總干擾力矩，也即角加速度信息，并將實際的控制效果和理論情況進行對比，從而進行故障情況判別；極性糾正策略的核心是基于控制效果的極性糾正，若故障辨識結果為極性錯誤，則進行極性對調，并對對調后的控制效果重復辨識，在符合預期的情況下完成極性糾正。

3.2 仿真驗證

為驗證本論文提出的噴管自適應故障辨識與極性糾正策略的有效性，以1.2節所述運載火箭為研究對象編寫仿真程序，以1.1節姿控噴管配置中的滾動通道為例設計了多次極性故障的場景進行數學仿真，仿真結果如下。

仿真設置滾動噴管極性多次極性故障的情景，故障注入時間分別為5 s、150 s、300 s，三通道角偏差、自抗擾辨識結果、極性故障標志字如圖4～ 6所示。

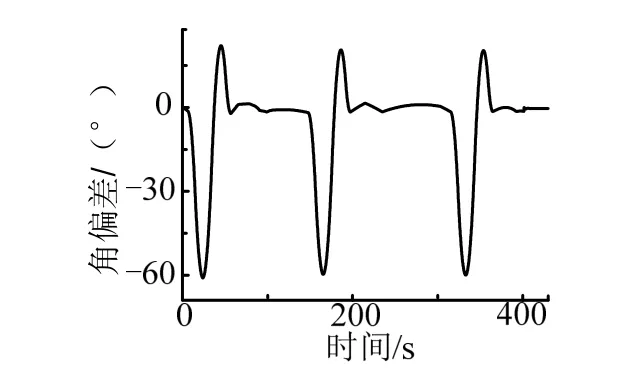
圖4 多次極性反號故障下滾動通道角偏差Fig.4 Rolling Channel Angle Deviation under Multiple Polarity Faults

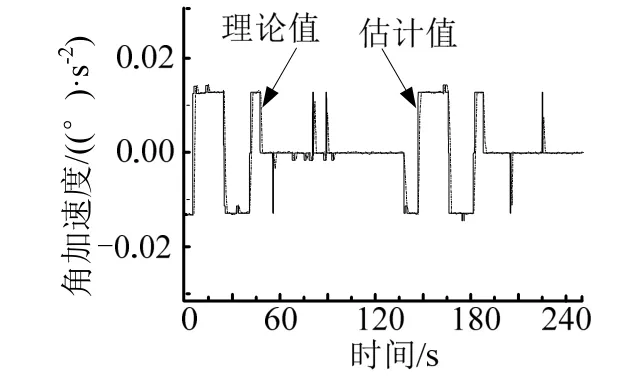
圖5 箭體滾動通道角加速度理論值和估計值對比Fig.5 Comparison of Theoretical and Estimated Rolling Angular Velocity

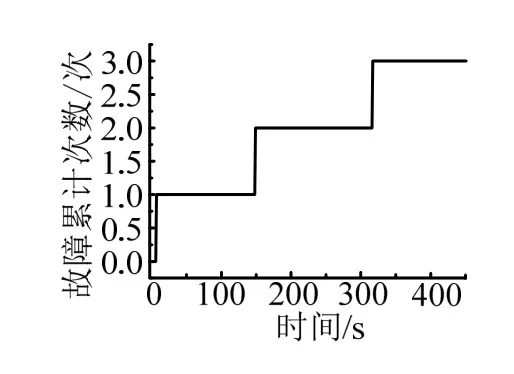
圖6 滾動通道極性故障累計次數Fig.6 Cumulative Number of Polarity Faults of Rolling Channel

由仿真曲線可知，當出現極性故障時，滾動姿態角偏差迅速增大，進入了故障判別分支，在很短的時間內辨識出了極性故障情況，在極性糾正策略下迅速進行了極性對調，角偏差迅速得到收斂，系統重新歸于穩定。在判別過程中實時計算的角加速度估計值（即“總干擾”）與理論值對比情況見圖5，可知擴張狀態觀測器所給出的估計值能夠較為準確地反映出箭體角加速度情況，為故障辨識提供了可靠的依據。圖6為仿真試驗給出的極性故障累計次數，和本次仿真用例注入的故障時間和次數一致，說明極性故障辨識準確有效。

4 結論

本文針對傳統基于噴管的控制方法應對飛行故障時姿態控制適應能力不足的問題，采用基于擴張狀態觀測器的自適應方法進行在線辨識，并基于辨識結果進行極性糾正策略設計。

仿真結果表明，設計的擴張狀態觀測器能夠較為準確地辨識出箭體所受的“總干擾力矩”（角加速度信息），結合動力學規律，能夠實現基于控制效果的噴管極性故障判別，并通過調換控制指令的策略完成故障噴管的極性糾正。多次極性故障的典型算例仿真結果證實了辨識方法和極性糾正策略的有效性。該方法簡單可靠、原理清晰、可移植性強，能夠有效提升控制系統的適應性和可靠性。