基于MATLAB對三維激光掃描數據的精度評定

袁 凱 李奎良 林志鵬

（四川電力設計咨詢有限責任公司，四川 成都 610041）

0 引言

與傳統測量相比，三維激光掃描技術的最大特點是能夠完整、快速以及高精度地獲取掃描對象的點云數據，建立掃描對象的三維模型，從而作出更具體、更形象化的分析與對比，實現了從單點測量到整個曲面測量的質的飛躍。三維激光掃描測量獲得的是由點云數據組成的數據模型，可以直觀地看出模型的形狀。目前，對于三維激光掃描數據的處理方法主要是通過對曲面的數據處理，其中，典型的樣條曲面包括B 樣條曲面、Bezier 曲面和 NURBS 曲面。曲面模型重建方案的選擇依賴于數據點本身的分布和排列情況，該處理方法都是通過對曲面的具體對比來提取某個位置點位的具體變化，從而推算某個區域的變形情況，其在本質上沒有太大的差別，而且曲面擬合方法的缺點是不能具體計算以達到的數據精度。傳統的數據處理雖然有同名點的比較，但是只能在單點比較中應用，不能在三維激光掃描的海量數據處理中應用[1]。根據曲面分析點位數據變化的分析難以精確判斷點位，容易出現錯位比較；并且，相關人員無法對所獲取的曲面數據進行具體的精度分析，使根據現有三維激光掃描數據處理方法獲得的測量成果的權威性難以得到保障。因此，該文提出首先將曲面轉換成曲線；其次，將曲線分解轉換成點；最后，結合MATLAB 對點云數據進行分析，從而達到對三維激光掃描數據進行精度評定的目的。

1 點云數據的預處理

由于地面三維激光掃描儀采集到的點云數據一般是通過從多個控制點上架設的儀器測量、掃描中獲取的，而且在掃描過程中由于儀器本身的系統誤差、測量對象表面粗糙度及各種偶然誤差的影響，使獲取的點云數據中會有大量的噪聲，在對數據進行分析時，需要對點云數據進行誤差分析及誤差改正。其中包括點云數據粗差的剔除、點云數據的拼接、噪聲數據的去除以及點云數據的濾波處理等，最終得到點云數據的三維模型。在點云數據的精拼接方面，以Besl 等提出的迭代最臨近點（ICP）算法為代表[2]。點云數據往往不能直接應用到實際工作中，需要進行拼接、濾波、精簡、分割及曲面重建等一系列的數據預處理。后來，Johnson 等人通過采用鄰近域搜索和多分辨率尺度搜索的方法對ICP 算法進行了改進，提高了其同名點的搜索效率和精度[3]。

2 點云數據轉化為單點數據

該試驗為了更加形象、精準地研究三維模型的整體精度，對三維激光掃描掃描數據進行精度評定，研究人員將從曲面數據中尋找具有代表意義的曲線數據，將曲線數據轉化成單點數據，再對單點進行精度評定。研究人員對點云數據預處理后進行曲面重建，按照曲面的形式展示出三維模型。目前可以將點云曲面重建方法大致分為隱式曲面重建方法、參數曲面重建方法和基于網格的曲面重建方法，該試驗選用的是參數曲面重建方法。

其次，當完成曲面重建后，再從曲面中劃分出具有代表意義和容易區分的點云線（盡可能地具有代表性），例如沿1 個垂直于Z軸的平面豎直剖開，將垂直于Z軸的平面看做無數條相同性質的點云線，選擇1 條點云線，也可稱為云剖線，就可以實現從曲面到曲線的轉換；再對這條云剖線進行分析，其變形信息就可以映射出曲面的變形信息。

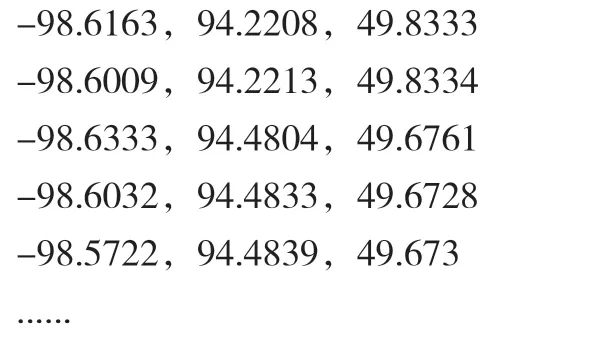
得到云剖線后，對云剖線上的節點進行曲線擬合，曲線擬合的方法主要包括最小二乘曲線擬合以及三次樣條曲線擬合、多次樣條曲線擬合。該試驗通過對比測試，最終選擇三次樣條曲線擬合方法； 三次樣條擬合函數就是運用三次樣條插值yy=Spline（x，y，xx），在給定的 （x，y） 離散點數據中，尋求1 個三次多項式，使其逼近每對數據 （x，y） 點的曲線，在點云線和擬合曲線上取相同的x值，與相應的y值進行比較；首先，將測量數據輸入RiSCAN_PRO 軟件中，將點云線的三維坐標以txt 的格式導出。導出的數據結果（x，y，z）如下所示。

再次，通過如下代碼在MATLAB 中實現三次樣條擬合曲線。

最后，對擬合后的曲線進行分析。

經過上面的步驟，可以轉化成對曲線進行分析。在擬合過程中，為了保證三維激光曲線擬合的一般性，需要選擇其中的部分點位作為該試驗的標靶點。研究人員將得到的標靶點擬合坐標值與實測值進行對比，其對比結果見表1。

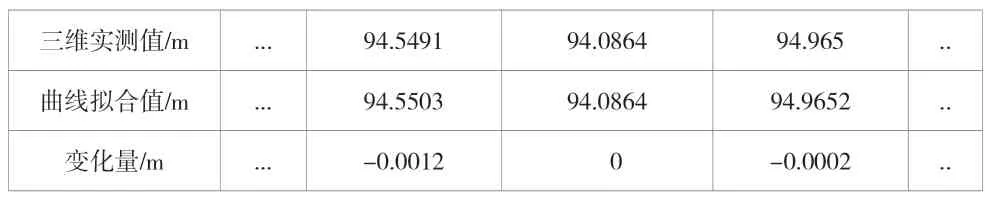
表1 實測值與擬合值的統計表

根據相關指數擬合公式可以計算其擬合度，如公式（1）所示。

公式（1）為檢驗曲線的擬合程度，對于已經獲取的樣本數據來說，R2的實測值和擬合值為確定的數。因此，R2越大，就表示殘差平方和越小，即模型的擬合效果越好；R2越小，就表示殘差平方和越大，即模型的擬合效果越差。在線性回歸模型中，R2表示解釋變量對預報變量變化的貢獻率。R2越接近1，表示回歸的效果越好。該試驗中R2=0.9998。經試驗對比，發現三次樣條曲線擬合的方式與點云數據的擬合效果比最小二乘曲線及多次樣條曲線的擬合效果更好。因此，該文采用基于MATLAB 的三次樣條曲線擬合方法獲取樣條曲線。

研究人員可以將測得的點云數據（三維模型）用擬合曲線來代替，每期都做同樣的曲線擬合，再比較曲線上標靶點的三維坐標。從而得出點云數據中標靶點的變化量。例如，在擬合曲線y=f（x）中，每間隔1 cm 取x的變形點，就可以得到其每個變形點的變形，其中1、2 期的變形結果見表2。

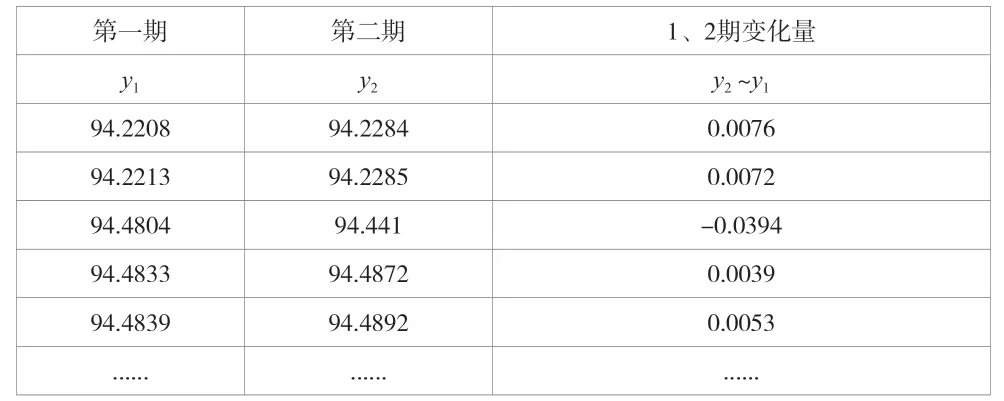
表2 利用曲線擬合得出1、2 期變化量

3 對三維激光掃描數據的精度評定

該實驗采用的對比儀器為徠卡TS30（測量機器人），由于測量機器人的精度比三維激光掃描儀的測量精度高2 個數量級，因此，用TS30 測量的數據為真值數據，可以有效地分析出三維激光掃描儀的精度。

三維激光掃描儀與全站儀獲得點位三維坐標的原理相同，它們的精度都受角度和距離誤差的影響；另外三維激光掃描儀主要還受激光信號信噪比、周圍噪聲的強度、回波信號的強度以及外部環境等誤差的影響，上述誤差可以分為系統誤差、偶然誤差以及儀器固有誤差[3]。

三維激光掃描儀和TS30 的精度可以分為內精度和外精度。內精度是指操作儀器時產生的人為誤差；為了測量內精度，研究人員必須將三維激光掃描儀對中、整平后，首先監測J1、J2、J3（滑坡上的監測點）的三維坐標；其次，取下儀器重新對中、整平；最后，再次監測J1、J2、J3的三維坐標。為了計算其中的定向精度，研究人員將三維激光掃描對中、整平后，連續2 次測得J1、J2、J3的三維坐標。外精度是指儀器本身的誤差，該試驗利用高精度的TS30 用同樣的方法連續2 次測量J1、J2、J3的三維坐標，以其測量結果作為檢驗標準，對三維激光掃描數據進行精度評定。

首先，用三維激光掃描儀對監測點J1、J2、J3進行2 次掃描，測得的差值結果見表3。

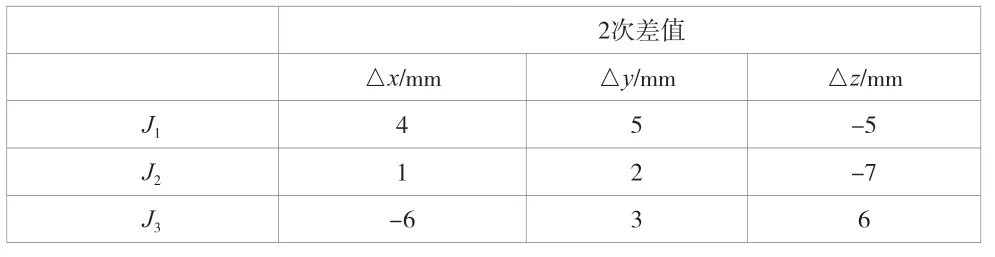
表3 三維激光掃描儀2 次差值的對比

其次，用TS30 對監測點J1、J2、J3進行定向測量，測得的差值結果見表4。

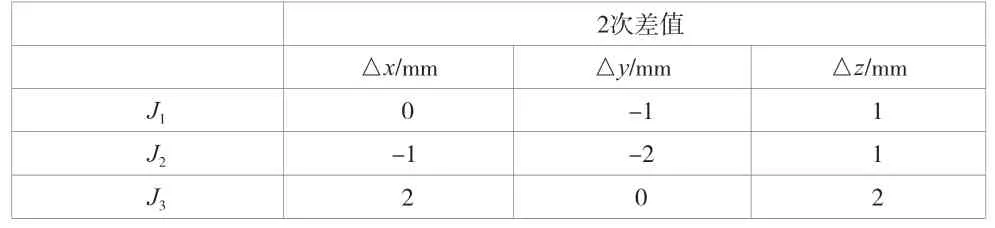
表4 TS302 次差值的對比

再次，用三維激光掃描儀和TS30 分別對監測點J1、J2、J3進行測量，測得的差值結果見表5。

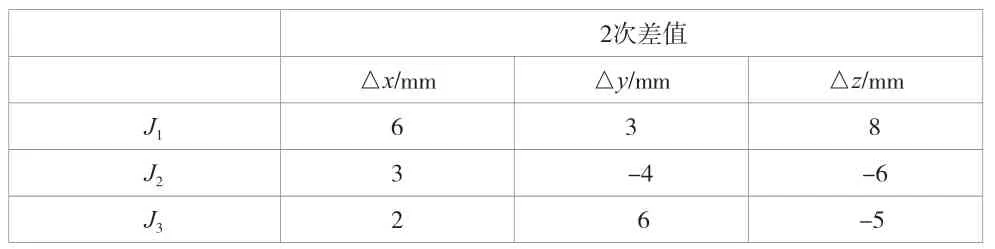
表5 三維激光掃描儀和TS30 2 次差值的對比

最后，計算在監測點J1、J2、J3取得數據的中誤差，結果見表6。

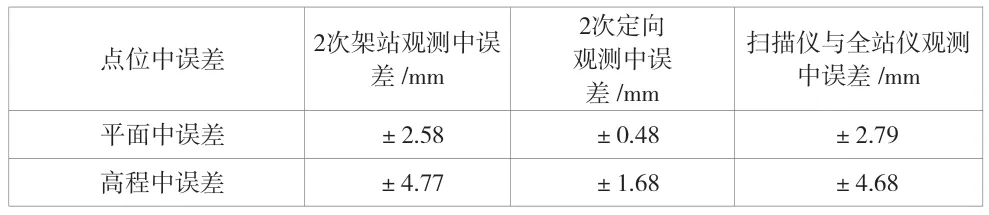
表6 中誤差計算表

根據上述誤差分析，2 次架站觀測誤差主要包括儀器量取誤差、儀器對中誤差、定向誤差和部分系統誤差；定向誤差明顯偏小，主要是消除了儀器量取誤差、儀器對中誤差和部分系統誤差。由表6 可以看出，TS30 觀測與掃描儀觀測的數據精度和2 次架站觀測的數據精度相差不大，因此，驗證了三維激光掃描儀在滑坡變形監測上的可行性。

4 試驗與分析

研究人員對在遼寧省某地進行的三維激光掃描數據進行試驗。首先，對該地進行坡體掃描，獲得各站測的三維點云數據；用RiSCAN_PRO 軟件對所有數據進行點云數據的預處理；對各測站點的云數據進行后視定向操作之后，利用ICP 拼接功能進行點云數據的拼接，拼接效果如圖1 所示。

圖1 點云數據拼接效果圖

其次，對預處理后的點云數據進行曲面重建，并從曲面中剖分出點云線，再選出標靶點。在RiSCAN_PRO 軟件中切出的點云線，如圖2 所示。

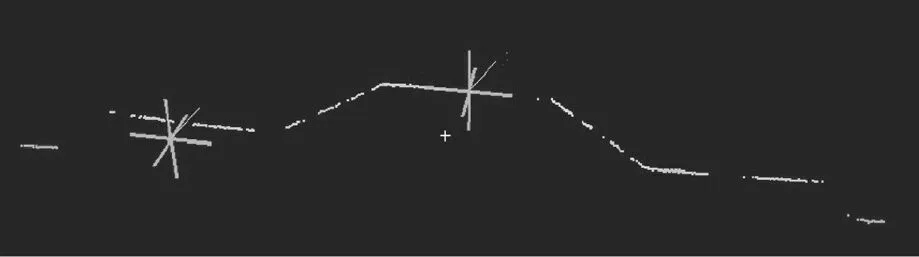
圖2 剖出的點云線

再次，在RiSCAN_PRO 軟件中，將點云線的三維坐標以txt 的格式導出，其結果如下。

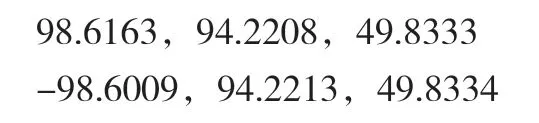
再利用MATLAB 對導出的數據進行三次樣條曲線擬合，得到的擬合圖形如圖3 所示。

最后，比較曲線上的點，每隔1 cm 取x方向的變形點得出點云數據的變化量，并將該變化量作為該變形點的變形，從而直觀地得到點云數據的精度評定。再根據點位的位移變化量來分析坡體的變形情況。

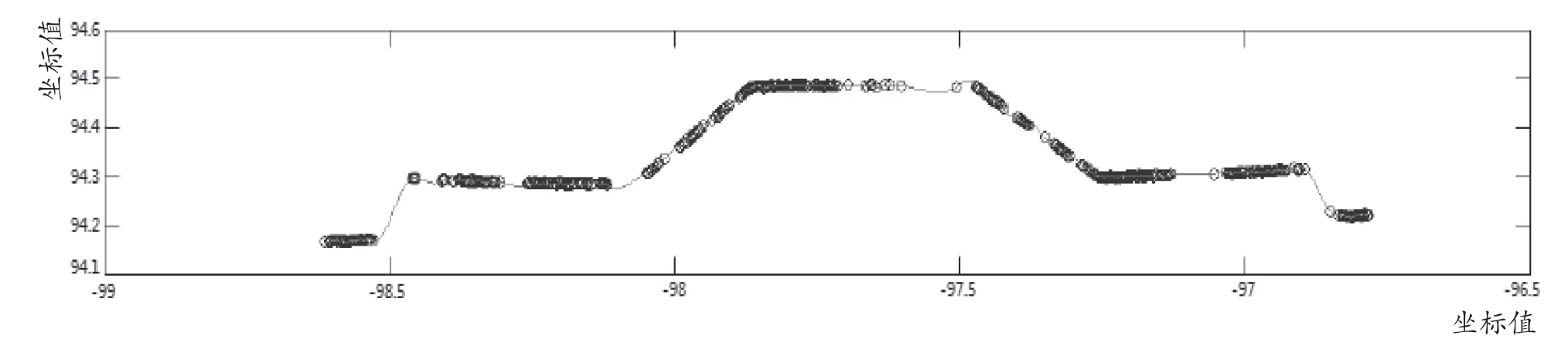
圖3 三次樣條擬合曲線

5 結語

根據該試驗的結果，三維激光掃描數據可以通過剖析、分解數據再結合高精度儀器進行精度評定；MATLAB所做的只是曲線擬合，只能代替從曲面中剖出的點云線，最終目的是方便尋找同名點，從而計算同名點間的變化量。

TS30 的精度比普通全站儀高很多，經過改進后，其在自由設站中也可以滿足對滑坡變形的監測需求。

在對三維激光掃描的數據處理中，三次樣條擬合法具有很好的擬合效果，經過線形擬合，可以將離散的點線性化。研究人員可以對擬合曲線進行比較，從而獲得點位的變化量，得到更好的分析結果。

該文在研究多源數據融合及精度分析中仍存在不足，其原因是目前對該地的監測期數不夠充分，對三維激光掃描儀和TS30 的數據處理還需要進行進一步研究。