菠蘿蜜果酒分批發酵動力學模型研究

王少曼，張彥軍，吳剛，徐飛，胡榮鎖，譚樂和

(中國熱帶農業科學院 香料飲料研究所，海南 萬寧, 571533)

菠蘿蜜(ArtocarpusheterophyllusLam.)又稱波羅蜜，屬于桑科(Moraceae)波羅蜜屬(Artocarpus)植物，是典型的特色熱帶果樹和木本糧作物，主要分布在印度、孟加拉國、中國和一些東南亞熱帶地區[1-2]。菠蘿蜜果肉占果實重量的30%～35%，果肉肥厚、香味濃郁，被譽為“熱帶水果皇后”，富含菠蘿蜜多糖、酚類化合物、類胡蘿卜素等生物活性物質，具有抗氧化、輔助降血糖、提高免疫力等有益的生理作用[3-6]。但是由于菠蘿蜜鮮果肉的高糖低酸環境，其極易遭受腐敗微生物的侵染而縮短其儲藏期從而限制其商業化應用。菠蘿蜜果酒作為菠蘿蜜果肉的精深加工產品，可提高菠蘿蜜產品的附加值，目前對于菠蘿蜜果酒的研究報道主要集中在菠蘿蜜果酒的菌種選育[7]、發酵工藝[8]、香氣成分[9]、生物活性成分[10]和抗氧化活性評價[11]研究，而關于菠蘿蜜果酒發酵過程酵母菌體生長、還原糖基質消耗和乙醇產量生成的動力學變化規律尚未研究報道。

菠蘿蜜果酒發酵過程中酵母菌體生長、還原糖基質消耗和乙醇產量生成的變化都存在一定的規律。微生物發酵動力學主要討論的正是微生物發酵過程中菌體生長、底物消耗和產物生成之間的動態平衡和內在規律，通過數學模型定量描述發酵過程的速率及影響速率的因素[12]。目前，許多研究已通過建立不同發酵型果酒如紅心火龍果酒[13]、仙人掌果酒[14]、山葡萄酒[15]、草莓果酒[16]、芒果酒[17]等的發酵動力學模型來描述酵母數目、糖消耗和乙醇生成量的規律，研究結果表明Logistic 、SGompertz、Boltzmann和DoseResp均能較好地體現菌體濃度、底物濃度和生成物濃度間的關系。然而，每種果酒因自身發酵環境不同而適用的發酵動力學模型存在一定差異。

本研究擬采用經典的Logistic、SGompertz、Boltzmann和DoseResp，對菠蘿蜜果酒發酵過程中酵母菌體生長、還原糖基質消耗和乙醇產量生成的變化規律進行非線性擬合，建立菠蘿蜜果酒分批發酵動力學模型，為菠蘿蜜果酒的分批發酵向連續發酵的過渡和工業化發酵工藝控制提供理論支持。

1 材料與方法

1.1 材料與試劑

菠蘿蜜，品種為香飲所11號，采摘于海南省萬寧市興隆熱帶植物園；RV171型葡萄酒活性干酵母(Saccharomycescerevisiae)，安琪酵母股份有限公司；果膠酶(500 U/mg，BR級)，上海源葉生物科技有限公司；亞硫酸氫鈉(分析純)，阿拉丁試劑(上海)有限公司；3, 5-二硝基水楊酸(化學純)，國藥集團化學試劑有限公司；氫氧化鈉、無水乙醇、四水合酒石酸鉀鈉、苯酚、無水亞硫酸鈉、蔗糖、葡萄糖(分析純)，西隴科學股份有限公司。

1.2 儀器與設備

AL104電子天平，梅特勒-托利多儀器(上海)有限公司；HX-PB908多功能料理機，佛山市海迅電器有限公司；DK-98-11A電熱恒溫水浴鍋，天津市泰斯特儀器有限公司；手持糖量折光儀(WZS-80)，上海儀電物理光學儀器有限公司；LRH-250F生化培養箱，上海一恒科學儀器有限公司；GI54DW自動壓力蒸汽滅菌鍋，致微(廈門)儀器有限公司；HR50-ⅡA2生物安全柜，青島海爾特種電器有限公司；血球計數板，上海市求精生化試劑儀器有限公司；CX31RTSF生物顯微鏡，奧林巴斯(中國)有限公司；SPECORD 250PLUS紫外/可見分光光度計，德國耶拿分析儀器股份公司；Z36HK臺式高速冷凍離心機，賀默(上海)儀器科技有限公司；酒精計，河北省武強縣華歐儀器儀表廠；TC-15套氏恒溫器，海寧市新華醫療器械廠；DLSB-5L-10 ℃低溫冷卻液循環泵，鞏義市河洛大研儀器廠。

1.3 實驗方法

1.3.1 菠蘿蜜果酒發酵工藝流程

菠蘿蜜果酒發酵工藝流程如下：

菠蘿蜜果實→去果皮和種子、取果肉→打漿→酶解→調節糖度→滅菌→接種→恒溫發酵培養→菠蘿蜜果酒→樣品測定

挑選成熟、無病蟲害腐爛的菠蘿蜜果實，切分除去果皮和種子，取出果肉，按照1∶2(g∶mL)比例添加蒸餾水打漿。用40 mg/L的果膠酶進行果漿酶解，酶解溫度為45 ℃，酶解時間為3 h。添加蔗糖調整菠蘿蜜果漿糖度至21 °Bx。加入一定量的亞硫酸氫鈉使果漿中的SO2含量達40 mg/L。果漿在60 ℃ 條件下滅菌30 min，然后冷卻至室溫，接種活化后的酵母(將一定量的干酵母用10倍量的含有1/3菠蘿蜜果漿和2/3滅菌蒸餾水的混合液在35 ℃條件下活化30 min)，使果漿中的干酵母用量達400 mg/L。恒溫發酵一段時間得到菠蘿蜜果酒樣品，發酵控溫為24 ℃，發酵時間為168 h，每24 h取樣分析測定。

1.3.2 檢測方法

1.3.2.1 酵母菌數量檢測

根據胡永正等[18]的方法有所改動，采用血球計數板對果酒發酵液中酵母菌數直接計數，實驗所用計數板為25×16型。取果酒發酵液用無菌水稀釋至適當的倍數，取少量滴在血球計數板上，蓋上蓋玻片，在生物顯微鏡下觀察計數酵母菌個數。按公式(1)計算酵母菌數量：

酵母菌數/(CFU·mL-1)

(1)

1.3.2.2 還原糖含量檢測

采用3, 5-二硝基水楊酸(3, 5-dinitrosalicylicacid, DNS)比色法測定果酒發酵液中的還原糖含量[19]。DNS試劑按照農業部標準配制，葡萄糖標準曲線回歸方程為y=0.436 1x+0.067 7，相關系數R2=0.997 4。

1.3.2.3 酒精度檢測

按照GB 5009.225—2016《食品國家安全標準 酒中乙醇濃度的測定》規定[20]，發酵液先蒸餾，然后采用酒精計法測定菠蘿蜜果酒中的酒精度。酒精度表示在20 ℃條件下的乙醇體積分數。

1.4 數據處理與分析

1.4.1 數據處理

每組實驗重復3個平行，結果取其平均值，采用Origin 9.0對數據進行統計與作圖分析，選取合適的動力學模型對酵母菌體生長、還原糖基質消耗和乙醇產量生成情況進行非線性擬合，并利用每個模型的擬合系數R2作為可靠性評價標準來篩選出擬合度高的動力學模型進行定量描述。

1.4.2 發酵動力學模型

酵母菌體生長動力學模型擬合：根據實驗數據分析，酵母菌體的生長呈“S”型曲線，結合經驗模型，選取Logistic、SGompertz和Botlezman模型進行非線性擬合，選取擬合R2系數最大的模型對描述酵母菌體生長規律[14]。

乙醇產量生成動力學模型擬合：乙醇是酵母菌轉化糖類代謝而生成的產物，其生成速率與酵母細胞生長速率有密切聯系，屬于生長偶聯型，呈現“S”型曲線，因此選用Logistic、SGompertz和Botlezman經典模型對其進行非線性擬合，選用擬合系數R2最大的模型描述乙醇產量生成[21]。

還原糖基質消耗動力學模型擬合：酵母發酵果酒過程消耗還原糖基質作為能量來源并產生乙醇，因此選用Logistic、DoseResp與Botlzman模型進行非線性擬合，選用擬合系數R2最大的模型描述還原糖基質消耗情況[22]。

2 結果與分析

2.1 菠蘿蜜果酒發酵過程中酵母菌數、還原糖含量和酒精度變化趨勢

釀酒酵母(S.cerevisiae)分批發酵菠蘿蜜果漿過程中酵母菌數、還原糖含量和酒精度變化如圖1所示。釀酒酵母經過稀濃度菠蘿蜜果漿的活化后能快速適應高濃度菠蘿蜜果漿的發酵環境，在48 h的發酵期，由于養分充足酵母菌數進入對數生長期，呈指數趨勢生長。隨后因為還原糖基質的消耗和乙醇代謝產物的積累，酵母菌體的生長速率下降，細胞死亡速率上升，當兩者狀態平衡時，酵母菌數進入穩定期[22]，此時酵母菌數最高達到5.27×108CFU/mL。96 h后酵母菌數開始進入衰亡期，可能是發酵環境中還原糖基質和酵母細胞內所儲能量消耗殆盡，酵母細胞在自身酶的作用下發生自溶而導致酵母菌數量的減少[23]。釀酒酵母發酵菠蘿蜜果漿過程消耗還原糖基質產生酒精，體系中的還原糖含量隨著發酵時間的增加而減少，至72 h時基本被酵母菌消耗完全，含量下降至3.30 g/L，與酵母菌體的生長時間點相一致。酒精是酵母菌厭氧發酵過程中轉化糖類代謝而生成的產物。酒精度隨著發酵時間的延長呈逐漸上升的趨勢，發酵48 h前，因酵母菌的快速增長和還原糖的快速消耗，酒精亦快速生成，到達72 h時，酒精度達到最大值，為10.8%vol，表明酒精的生成與酵母菌生長和還原糖消耗是相對應的。

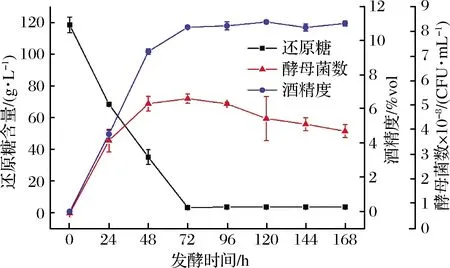
圖1 菠蘿蜜果酒發酵過程中酵母菌數、還原糖含量和酒精度變化規律Fig.1 Changes of yeast count, reducing sugar content and alcohol content during fermentation of jackfruit wine

2.2 菠蘿蜜果酒發酵動力學模型的建立

2.2.1 酵母菌體生長動力學模型

由圖1可知，釀酒酵母在菠蘿蜜果漿的發酵環境中96 h后進入菌體衰亡期，而在發酵0～96 h處在對數生長期和穩定期，因此本研究擬對發酵0～96 h時期的酵母菌體生長情況進行非線性擬合。Logistic、SGompertz和Boltzmann模型對酵母菌體生長情況的非線性擬合結果如表1和圖2所示。由圖2的擬合曲線分析可知，模型擬合下的酵母菌生長曲線在菠蘿蜜果酒發酵72 h后趨于穩定，在72 h時酵母菌體數量達到最高值。從表1的擬合方程和擬合系數分析可知，3種模型均能很好地預測酵母菌體的生長狀況。相比于Logistic模型(R2為0.993 59)和SGompertz模型(R2為0.992 03)，Boltzmann模型的擬合系數R2為0.993 96，對酵母菌的生長情況的擬合效果最佳。因而Boltzmann模型比其他2個模型更適合對菠蘿蜜果酒中酵母菌生長情況進行定量描述。

表1 酵母菌體生長的擬合方程及其擬合系數Table 1 Fitting equation of yeast growth and its fitting coefficient

2.2.2 乙醇產量生成動力學模型

采用Logistic、SGompertz和Boltzmann模型對菠蘿蜜果酒發酵過程乙醇產量生成情況進行擬合，菠蘿蜜果酒發酵過程酒精度實際值與擬合曲線如圖3所示。3種模型擬合下的酒精生成曲線與圖2中的酵母菌生長曲線基本同步，酵母菌在對數生長期內代謝產生酒精的增長速度迅速增加，酒精度在菠蘿蜜果酒發酵72 h后趨于穩定，在72 h時酒精度達到最大值。3種模型的擬合方程和擬合系數如表2所示，Logistic、SGompertz和Boltzmann模型的擬合系數R2分別為0.997 94、0.999 05和0.999，SGompertz和Boltzmann模型的R2比Logistic模型的R2值更趨近于1.0，說明SGompertz和Boltzmann模型均能較好地描述菠蘿蜜果酒發酵過程乙醇的動態增長過程。

表2 乙醇產量生成的擬合方程及其擬合系數Table 2 Fitting equation of ethanol production and its fitting coefficient

a-Logistic模型；b-SGompertz模型；c-Boltzmann模型圖2 發酵動力學模型下的酵母菌生長擬合曲線Fig.2 Growth fitting curve of yeast under fermentation kinetics model

a-Logistic模型；b-SGompertz模型；c-Boltzmann模型圖3 發酵動力學模型下的乙醇產量生成擬合曲線Fig.3 Fit curve of ethanol production under fermentation kinetics model

2.2.3 還原糖基質消耗動力學模型

Logistic、DoseResp和Boltzmann模型對還原糖含量的擬合方程、擬合系數和擬合曲線見表3和圖4。由圖4可知，3種模型對還原糖的擬合曲線趨勢基本一致，在菠蘿蜜果酒發酵的前72 h，還原糖消耗量逐漸增大，在發酵72 h后，酵母菌數和酒精度的變化趨于穩定，還原糖含量變化亦趨于穩定，這也表明菠蘿蜜果酒主發酵的結束。由表3可知，3種模型對于還原糖基質的消耗擬合效果相較于酵母菌數和酒精度的較差，Logistic、DoseResp和Boltzmann模型的擬合系數R2分別為0.978 46、0.987 05和0.987 05，DoseResp和Boltzmann模型的擬合系數一致，均高于Logistic模型，說明2種模型均能較好地反映菠蘿蜜果酒發酵過程還原糖消耗的變化。

表3 還原糖基質消耗的擬合方程及其擬合系數Table 3 Fitting equation of reducing sugar consumption and its fitting coefficient

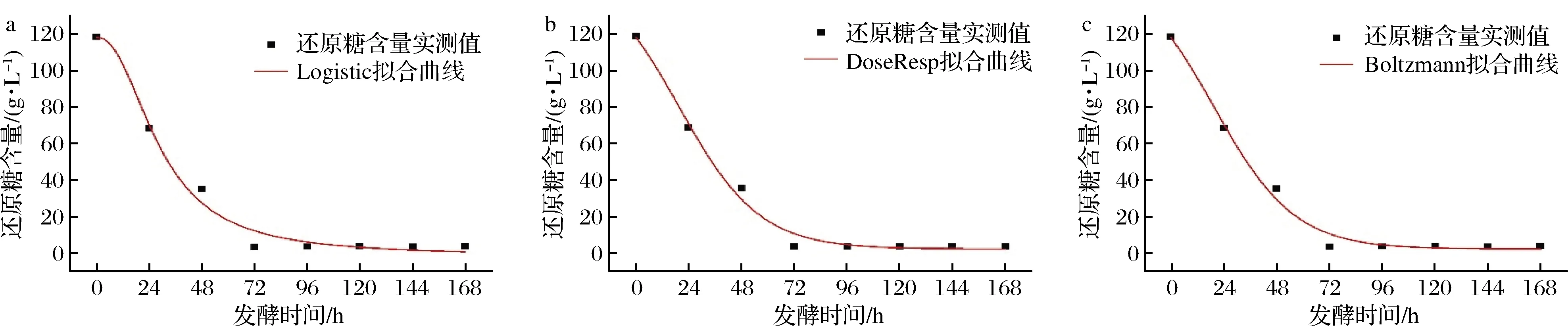
a-Logistic模型；b-DoseResp模型；c-Boltzmann模型圖4 發酵動力學模型下的還原糖基質消耗擬合曲線Fig.4 Fit curve of reducing sugar consumption under fermentation kinetics model

在微生物的生長過程中，最活躍的時期是對數生長期，伴隨營養物質的貯存和初級代謝產物的產生，微生物的發酵行為可通過數學模型被清楚地描繪[24]。李雪等[14]應用Logistic、SGompertz、DoseResp和Boltzmann模型對仙人掌果酒的酵母菌數、酒精度、還原糖量進行非線性擬合，擬合度均大于0.99。張琪等[22]采用Logistic、DoseResp、Boltzmann和SGompertz等模型對黑加侖果酒發酵過程的擬合結果均呈現較好的擬合效果。李俠等[21]同樣用上述4個模型擬合紅棗酒的發酵過程，分別呈現出SGompertz、Boltzmann和 DoseResp模型對酵母生長、乙醇生成、還原糖消耗的擬合度最高，研究結果與本研究的情況一致，本研究采用SGompertz、Boltzmann模型對乙醇產量生成的擬合系數能達到0.999。而實驗中DoseResp和Boltzmann模型對還原糖的擬合系數只有0.98，與張琪等[25]的研究情況一致，可能是由于釀酒酵母生長繁殖旺盛，在72 h時已將還原糖幾乎消耗完全，實驗值低于擬合模型的預測值。

3 結論

本研究采用經典的Logistic、SGompertz、Boltzmann和DoseResp發酵動力學模型對菠蘿蜜果酒分批發酵過程的酵母菌體生長、還原糖基質消耗和乙醇產量生成進行非線性擬合，選用擬合系數R2對擬合模型進行可靠性評價。模型均能較好的描述菠蘿蜜果酒發酵過程的動力學特征，Boltzmann模型能更好地適用于酵母菌體生長、還原糖基質消耗和乙醇產量生成的模擬。本實驗的發酵動力學研究可以預測實驗指標，從而為菠蘿蜜果酒大型的發酵工藝控制提供理論基礎。