一種面向邊緣環境的多實例服務鏈在線部署算法*

宋 滸，甘讓興，夏 飛，鄒昊東

(1.南京大學計算機軟件新技術國家重點實驗室,江蘇 南京 210023;2.國網江蘇省電力有限公司信通分公司，江蘇 南京 210023)

1 引言

企業使用邊緣計算技術將服務部署在離用戶更近的邊緣設備上，以滿足用戶對超低時延服務(虛擬現實[1]、流媒體[2]、自動駕駛[3]和圖像處理程序[4]等)的需求。同時，虛擬化技術使網絡功能脫離了專用硬件的束縛，能夠靈活地部署在虛擬機和容器等設備虛擬實例上，大大降低了企業的成本，并且用戶可以根據自身需求，將豐富的虛擬網絡功能以服務鏈[5]的形式組合在一起，以提供不同的網絡服務[6,7]，這極大地提高了邊緣設備部署網絡功能的靈活性和有效性。

但是，承載網絡功能服務的邊緣設備(無線路由器、網關等)通常只有有限的硬件資源[8,9]。例如，近年來發布的TP-LINK Archer C9無線路由器僅有1 GHz雙核CPU[10]。面對不斷增長的業務流量，這些資源有限的邊緣設備極易發生過載現象。另外，隨著物聯網的高速發展，企業在城市周圍部署了越來越多的智能設備，這些設備將收集大量的數據，導致在網絡邊緣處理的流量變化較大。智能設備上運行的應用程序流量模式的不同也會影響設備的負載。這些流量頻繁變化的用戶請求同樣會造成邊緣設備過載。

為了應對邊緣設備過載問題，首先需要對服務鏈的資源消耗進行精準的測量。服務鏈的資源消耗主要指網絡功能計算所需要的資源消耗。文獻[11]表明，數據包傳輸在邊緣設備上會消耗大量的資源，而已有工作通常忽略這類資源消耗。本文對服務鏈負載模型進行了細粒度建模，充分考慮了網絡功能計算和數據包傳輸2種類型的資源消耗。相比已有的研究，本文設計的負載模型對服務鏈中多實例的資源消耗進行了更準確的建模。面向邊緣環境的多實例服務鏈部署模型，包括邊緣設備負載模型和基于虛擬實例通信的時延約束模型2個組成部分。在此基礎上形式化地描述了最小化最大邊緣設備CPU負載率的最優化問題。

基于細粒度的服務鏈負載模型，本文證明了多實例服務鏈在線部署問題為NP難問題。因此，為了能在滿足時延約束的情況下，在邊緣環境進行多實例服務鏈的部署，以期望達到邊緣環境下邊緣設備間負載均衡的效果，本文設計了面向邊緣環境的多實例服務鏈在線部署算法。該算法包括3個階段：(1)時延滿足路徑搜索:查找當前網絡拓撲下滿足時延約束的路徑集合；(2)部署路徑選擇:選擇路徑集合內的一些路徑部署服務鏈；(3)網絡功能部署:將服務鏈的網絡功能按照用戶要求的部署策略部署在優選的路徑集合內的邊緣設備上。

仿真實驗表明，該算法在最大邊緣設備CPU負載率這一評價指標上優于忽視服務鏈網絡功能間存在通信開銷的基準算法。通過對比小規模網絡拓撲的最優部署結果，該算法結果接近最優部署結果。

本文的組織結構如下：第2節通過路由器容器部署實驗分析影響網絡功能實例的CPU負載的因素；第3節對多實例服務鏈在線部署問題進行建模；第4節對部署問題進行算法設計；第5節對部署算法進行評估；第6節對本文內容進行總結。

2 容器化網絡功能通信開銷

為了應對邊緣設備過載問題，本文首先對提供服務的服務鏈網絡功能的資源消耗進行細粒度的測量。本文在無線路由器內通過容器化部署服務鏈設計了一個基準實驗。實驗中使用了一個無線路由器和一臺服務器。無線路由器中部署虛擬網絡功能鏈，服務器同時作為流量的發送方和接收方。該實驗將服務鏈的網絡功能設置為數據包轉發過程，忽略網絡功能計算資源的消耗，從而得到數據包在網絡功能間傳遞的通信開銷。通過調整服務鏈長度、數據包速率和數據包大小3個關鍵參數，同時持續讀取無線路由器CPU利用率，得到CPU利用率與3個參數的關系。通過控制變量的方式。分別分析了CPU利用率和服務鏈長度、數據包速率和數據包大小的關系，實驗結果如圖1所示。圖1中采樣點代表實驗數據，通過最小二乘法得到擬合線(未進行實驗時，無線路由器的CPU利用率為1%～2%，所以擬合線未過原點)。

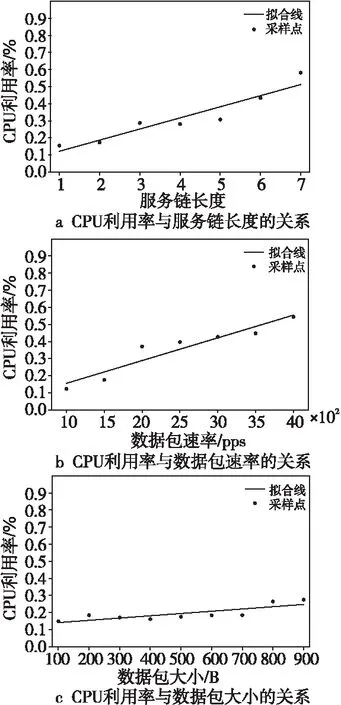
Figure 1 Relationship between CPU utilization and service chain length, packet rate and packet size

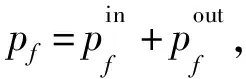
load(T)=comm(T)+comp(T)=

(1)

其中，αf是網絡功能f計算開銷和通信開銷的比率。注意到，該模型不同于傳統的僅考慮計算開銷的服務鏈負載模型(簡稱為服務鏈負載傳統模型)：

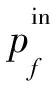
(2)

另一方面，為了降低設備的負載，提高服務的穩定性，通常會在不同設備的虛擬實例內部署同一網絡服務[12-14]，在對用戶流量進行劃分后通過部署某個網絡功能的多個虛擬實例實現負載均衡。但可惜的是，目前缺乏結合上述2個方面的服務鏈部署算法研究工作。因此，本文設計并實現了一種面向邊緣環境的多實例服務鏈在線部署算法，在現有的邊緣環境下，提供低時延、低負載的網絡功能服務。

3 多實例服務鏈在線部署問題建模

在邊緣環境下存在著大量的邊緣設備，這些邊緣設備的CPU和內存資源使用情況各不相同。企業可以使用這些邊緣設備，將服務鏈中的網絡功能部署在具有較低負載和較近距離的對等邊緣設備上，提供低時延的服務，同時緩解設備過載的問題。本節在模型假設的基礎上，首先對邊緣環境進行建模；然后通過虛擬實例通信圖來描繪多實例服務鏈部署的通信情況；接著，提出了衡量設備負載的邊緣設備負載模型和概括服務鏈時延約束的時延約束模型；最后，給出了問題求解的目標函數和難度論證。

3.1 模型假設

由于邊緣設備的資源有限性，本文假定虛擬實例以容器的方式部署在邊緣設備。為了簡化邊緣環境模型，本文采用如下假設：

(1)邊緣設備上運行的容器可以部署任意類型虛擬網絡功能VNF(Virtual Network Function)。

(2)任何虛擬實例只能部署一個虛擬網絡功能。

(3)僅關注邊緣設備之間的傳播時延，不考慮設備內部處理流量導致的傳輸時延。

3.2 邊緣環境模型

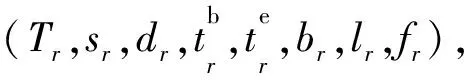
由于VNF實例可能改變通過該功能的流量大小，例如IPSec/SSL VPN和媒體網關會將通過的數據包進行封裝和解封裝操作而改變數據包的大小[15]；防火墻和入侵檢測系統會丟棄違反安全策略的數據包而改變數據包的數量[16]。本文定義αTr,i表示服務鏈第i個網絡功能改變流量的比率，βTr,i表示服務鏈第i個網絡功能計算開銷和通信開銷的比率。由于單位時間間隔內存在多個用戶部署服務鏈的情況，所以本文用符號N表示單位時間間隔內用戶請求的數量，并將時間間隔t內，對邊緣設備有負載作用的用戶請求集合表示為R(t)。邊緣設備v的負載容量表示為Cv。本文使用|X|表示集合[X]的大小，例如，符號|Tr|表示服務鏈長度，|Tr,i|表示部署服務鏈第i個網絡功能的實例個數。

3.3 虛擬實例通信圖

為了降低設備的負載，提高服務的穩定性，通常將服務鏈的網絡功能部署在多個邊緣設備容器中。虛擬實例通信圖能描繪服務鏈部署的情況。如圖2所示，圓形代表邊緣設備，方形代表虛擬實例，箭頭上方數字代表流量大小。例如，虛擬實例Tr,1,1和虛擬實例Tr,2,1有通信關系，而和虛擬實例Tr,2,2沒有通信關系。

Figure 2 An example of virtual instance communication graph

軟件定義網絡技術可以通過下發流表項到邊緣設備的方式調度用戶網絡流通過特定虛擬實例。但是，受網絡流數量|fr|的影響，部署服務鏈第i個網絡功能的虛擬實例個數需滿足以下不等式：

|Tr,i|≤|fr|,i∈[1,|Tr|]

(3)

等號成立當且僅當部署服務鏈第i個網絡功能的虛擬實例運行在完全不同的邊緣設備上。從圖2中可以看出，用戶請求從某網絡流的源節點出發，依次通過運行在邊緣設備v1、v2和v3上的VNF實例，最終到達目標節點。

3.4 邊緣設備負載模型

為了達到邊緣設備間負載均衡的目標，本文需要對邊緣設備的負載情況進行建模。部署服務鏈第i個網絡功能的虛擬實例的入口流量和出口流量的關系為：

(4)

由于信道不會改變流量大小，所以由流量守恒可知，部署服務鏈第i個網絡功能的虛擬實例j的入口流量等于和該虛擬實例有通信關系的部署第i-1個網絡功能的虛擬實例的出口流量之和：

(5)

其中，hTr,i-1,k,i,j∈{0,1}是通信二值變量，當hTr,i-1,k,i,j=1時，表示部署服務鏈第i-1個網絡功能的虛擬實例k和部署服務鏈第i個網絡功能的虛擬實例j有通信關系；否則，hTr,i-1,k,i,j=0。另一方面，初始帶寬等于部署服務鏈第1個000網絡功能的虛擬實例的入口流量之和：

(6)

在時間間隔t內，部署服務鏈第i個網絡功能的虛擬實例j的入口流量和邊緣設備v的關系為：

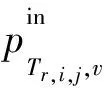
(7)

其中，xt,Tr,i,j,v∈{0,1}被稱為設備二值變量，當xt,Tr,i,j,v=1時，表示在時間間隔t內，部署服務鏈第i個網絡功能的虛擬實例j運行在邊緣設備v上；否則，xt,Tr,i,j,v=0。同理，在時間間隔t內，部署服務鏈第i個網絡功能的虛擬實例j的出口流量和邊緣設備v的關系為：

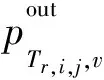
(8)

基于服務鏈網絡功能間存在通信開銷的服務鏈負載模型，在時間間隔t內，邊緣設備v的負載為：

loadv(t)=∑r∈R(t)((ω+αTr,i)·

(9)

同理，在服務鏈負載傳統模型下，在時間間隔t內，邊緣設備v的負載為：

(10)

3.5 時延約束模型

邊緣環境模型規定的流量必須通過源節點和目標節點。為了統一時延約束表示，本節為服務鏈添加2個不增加負載的網絡功能Tr,0和Tr,|Tr|+1，并將其分別置于服務鏈的首端和尾端(保持服務鏈長度不變，通過額外下標表示這2個假設的網絡功能)，而且人為規定部署網絡功能Tr,0的虛擬實例必須運行在源節點上，部署網絡功能Tt,|Tr|+1的虛擬實例必須運行在目標節點上，由式(11)表示如下：

(11)

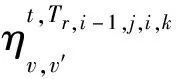
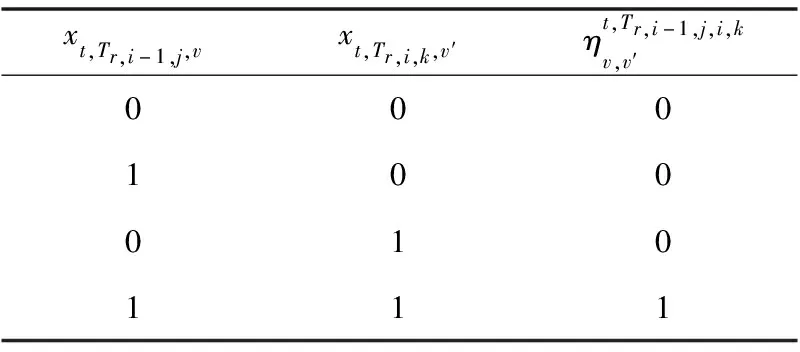
Table 1 Constraint relationship between equipment binary variable and delay binary variable

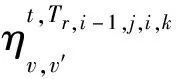
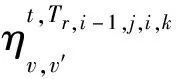
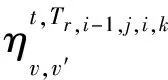
?t,?r∈R(t),?v,v′∈V,hTr,i-1,j,i,k=1

i∈[1,|Tr|+1],

j∈[1,|Tr,i-1|],k∈[1,|Tr,i|]

(12)

綜上可以得出，服務鏈的時延約束滿足不等式：

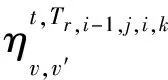
?r∈R(t),hTr,i-1,j,i,k=1,i∈[1,|Tr|+1],

j∈[1,|Tr,i-1|],k∈[1,|Tr,i|]

(13)

3.6 目標函數

s.t. (3)～(9),(11)～(13)

(14)

該目標函數F旨在時延約束以及所有時間間隔內，最小化最大邊緣設備CPU負載率，即對邊緣環境下的邊緣設備進行負載均衡。

求解該問題存在2個難點：(1)由于邊緣環境下用戶的移動性，用戶請求會頻繁加入和退出，不同于服務鏈的靜態部署，最大邊緣設備負載和時間維度有關；(2)邊緣設備的負載均衡問題必須同時考慮時延約束和網絡功能的負載差異性。一方面，時延約束限定了對等邊緣設備的選取；另一方面，網絡功能負載的差異性增加了在對等邊緣設備間保持負載均衡的難度。

3.7 NP完全性證明

首先，問題能在多項式時間內驗證候選解是否滿足約束條件。其次，本節首先簡短介紹已被證明為NP完全問題的多處理器調度MPS(Multi-Processor Scheduling)問題[17]，然后證明MPS問題可以歸約到F的一個子問題F1，該子問題是面向邊緣環境的只考慮計算開銷的線性服務鏈部署問題。

MPS：給定n個任務J={J1,J2,…,Jn}，每個任務需要pj時間去處理；m臺機器M={M1,M2,…,Mm}(n>m)，由這m臺機器來完成這n個任務。如何調度這些任務，使得最后完成所有任務的時間最短。

定義F1：在保持F其它條件不變的情況下，改變以下4個條件：

(1)用戶請求r流量內網絡流數量|fr|為1。

(2)時間間隔數量TN=1，且用戶請求數N=1。

(3)忽略服務鏈網絡功能間的通信開銷，即commTr,i=0。

(4)時延約束lr被設定為無窮大。

下面證明F1是NP難問題：

證明構造規約過程如下，將MPS問題的輸入構造成子問題的輸入，即服務鏈具有n個網絡功能，每個網絡功能會產生pj的計算開銷，邊緣環境下有m個邊緣設備。為達到設備間負載均衡當且僅當所有邊緣設備的負載情況相同。已知MPS問題的輸出，即所用時間最短當且僅當所有機器的處理時間相等。由于邊緣設備和機器具有一一對應關系,且在子問題以及MPS問題的輸出中,任意邊緣設備的負載和對應機器的處理時間在數值上相等。因此，在多項式時間內，MPS問題的輸入可以轉換成子問題的輸入，且子問題的輸出可以轉換成MPS問題的輸出，證畢。

□

該證明說明子問題F1是NP難問題，進而F是NP難問題，從而F是NP完全問題，除非能證明P=NP，否則不可能為F找到一個高效的多項式算法，基于求解問題F的難度論證，本文將在下一節中給出一個啟發式算法DS-PC-ND(Delay Statisfaction-Path Collection-Network function Development)去解決該問題。

4 DS-PC-ND算法設計

4.1 DS-PC-ND算法框架

為了能在滿足時延約束的情況下，在邊緣環境進行多實例服務鏈在線部署，以期望達到邊緣環境下邊緣設備負載均衡的效果，算法框架分為如下3個階段：

(1)階段1(時延滿足路徑搜索)：搜索當前網絡拓撲下滿足時延約束的路徑集合P1。

(2)階段2(部署路徑選擇)：選擇路徑集合P1內的|fr|個路徑組成路徑集合P2作為部署路徑集合。

(3)階段3(網絡功能部署)：將服務鏈的網絡功能按照某種部署策略部署在路徑集合P2的邊緣設備上。

這3個階段表明多實例服務鏈的部署涉及到將服務鏈分配到滿足時延約束的若干路徑(P2)上，并將服務鏈的網絡功能部署在路徑中資源較為充足的邊緣設備上。需要說明的是，由于網絡流數量|fr|不等于|P1|，所以階段2在時延約束路徑集合P1內選出部署路徑集合P2，這能簡化階段3內網絡功能部署的過程。算法框架如圖3所示。下面小節將依次介紹時延滿足路徑搜索DS(Delay Statisfaction)算法、部署路徑選擇PC(Path Collection)算法和網絡功能部署ND(Network function Development)算法。

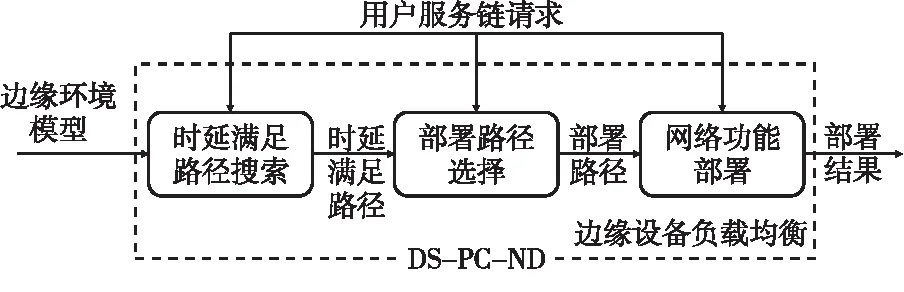
Figure 3 Framework of DS-PC-ND algorithm

4.2 時延滿足路徑搜索算法

由于邊緣環境模型假定用戶請求必須通過已知的源節點和目標節點，所以時延滿足路徑搜索可以看成在已知源節點和目標節點的情況下，找出滿足時延約束lr的路徑集合P1。為了降低問題的難度，本文假定時延滿足路徑搜索(DS)算法搜索的是簡單路徑，即路徑中的節點不能出現重復，這樣得到路徑集合P′1，顯然P′1?P1。

本文使用雙棧數據結構設計了一個基于剪枝搜索策略的非遞歸算法去求解時延滿足路徑搜索問題。如算法1所示，該算法首先準備2個棧(主棧S1和輔棧S2)，主棧中的每個元素是單個值，表示當前路徑的某個節點，輔棧中的每個元素是一個列表，表示主棧對應元素的鄰接節點集合，即主棧記錄的是某一條以源節點為起點的路徑，而輔棧記錄主棧路徑可能的下一跳。本文使用變量時延和delay來記錄目前主棧路徑的時延之和。當主棧棧頂元素為目標節點時，主棧棧底到棧頂的元素序列記為符合時延約束的一條簡單路徑。為了使選擇出來的路徑是簡單路徑，算法1保證主棧壓入的下一跳不會和主棧已有元素重復。函數Neig返回鄰接節點列表；函數First返回列表第1個元素；函數Remain表示將列表第1個元素去除后，組成一個新的列表；函數Seq返回棧底到棧頂元素序列；函數Delay返回2個節點之間的時延；函數RmRp(X,Y)去除列表X內Y包含的元素。

算法1時延滿足路徑搜索算法

輸入：圖G(V,E)，用戶請求。

輸出：滿足時延約束的簡單路徑集合P′1。

S1←sr，S2←Neig(sr)；

Repeat

neigs←S2.pop()；

If!neigs.empty()then

S2.push(Remain(neigs))；

next←Delay(S1.top(),First(neigs))；

Ifdelay+next≤lrthen

delay+=next；

S1.push(First(neigs))；

S2.push(RmRp(Neig(S1.top()),S1))；

Endif

Else

S1.pop();continue；

Endif

IfS1.top()==drthen

P′1.push(Seq(S1))；

delay-=Delay(S1.top(),S1.nextTop())；

S1.pop();S2.pop()；

Endif

UntilS1.empty()；

ReturnP′1；

4.3 部署路徑選擇算法

通過時延滿足路徑搜索算法，本文找到滿足時延約束的簡單路徑集合P′1。由于本文設定用戶請求內網絡流流通的路徑是固定的，且網絡流數量為|fr|，所以需要在P′1內選擇|fr|條路徑來作為部署服務鏈的部署路徑集合P2。但是，為了降低時間復雜度，本節使用嵌套TopK策略在路徑集合P′1中找出將要部署多實例服務鏈的路徑集合P2。本文將該算法稱為部署路徑選擇(PC)算法，其具體實現包含嵌套函數(函數1嵌入函數2內，作為函數2的一條語句執行，函數2返回最終的部署路徑集合P2)。

函數1內容說明：對于p∈P′1，本函數選取路徑p內負載最小的K1(|Tr|)個邊緣設備來代表路徑p內所有邊緣設備的負載情況，并將這K1個邊緣設備負載和的均值記為loadp，并將該值返回給函數2。

函數2內容說明：由于總共有|P′1|條路徑，而本函數的目標是選擇出|fr|(記為K2)條路徑作為部署路徑集合P2(該集合是算法3的輸入)，而一般情況下|P′1|都不等于|fr|，所以需要設計一種策略在P′1中選擇|fr|條路徑。本文設定函數2使用函數1返回的loadp值來進行選擇，即選取P′1內loadp值最小的|fr|條路徑(loadp值和p存在一一對應關系)。

基于嵌套TopK策略中，函數1和函數2包含嵌套關系，并且函數1和函數2的運算過程涉及到選擇K個元素(函數1中K=K1，函數2中K=K2)。

算法2部署路徑選擇算法(函數1)

輸入：時延滿足路徑集合P′1，用戶請求r，邊緣環境模型。

輸出：部署路徑集合P2。

初始化最大堆D1；

進入函數1(p由函數2傳遞給函數1)；

Foreachnode∈pdo

IfD1.top()>Load(node)then

D1.pop()，D1.push(Load(node))；

Endif

Endfor

loadp←D1內有效元素和的均值；

重置D1；

Returnloadp；

本文使用堆來處理TopK選擇問題，使用了2個最大堆D1和D2。維持D1大小為|Tr|，維持D2大小為|fr|。顯然，很容易得到函數1的時間復雜度為O(|p|·log2(|Tr|))，函數2的時間復雜度為O(|P′1|·log2(|f4|))，但由于函數1要運行|P′1|次，所以算法2的時間復雜度為O(|P′1|·|p|·log2(|Tr|)+|P′1|·log2(|fr|))。另一方面，由于算法2需要維護2個最大堆，所以該算法的空間復雜度為O(|Tr|+|fr|)。

4.4 網絡功能部署算法

得到了將要部署多實例服務鏈的簡單路徑集合P2后，本節設計了一個基于貪心策略的啟發式算法將多實例服務鏈的網絡功能部署在這些路徑上的邊緣設備上。如算法3所示，對于每一條部署路徑p∈P2，部署算法首先找到該路徑的最小負載節點node，然后將服務鏈的第1個網絡功能部署在該節點上,之后將部署路徑p的起點設置為node。如此往復，直至服務鏈的全部網絡功能部署完畢。

算法3網絡功能部署算法

輸入：部署路徑集合P2，用戶請求r，邊緣環境模型。

輸出：部署結果。

Foreachp∈P2do

ForeachTr,i∈Trdo

獲取p內最小負載節點node；

更新邊緣設備node的負載；

將p的起點設置為node；

Endfor

Endfor

算法3的時間復雜度為O(|P2|·|Tr|·|p|)，因為該算法包括2層循環，外層循環要進行|P2|次，內層循環要進行|Tr|次，內層循環中查找最小負載節點要對路徑p遍歷一次(時間復雜度為O(|p|))。該算法只使用常數個額外變量，空間復雜度為O(1)。

5 DS-PC-ND算法評估

對于多實例服務鏈在線部署算法DS-PC-ND，本文將從2個方面來評估其性能：一方面，由于服務鏈網絡功能間存在通信開銷，所以希望知道該算法能多大程度緩解負載失衡現象；另一方面，評估該算法與最優部署結果之間的差距。

5.1 仿真環境與仿真參數

仿真實驗在Linux環境下進行，使用LEMON網絡仿真庫[18]隨機生成2個網絡拓撲。網絡拓撲A包含30個節點和47條邊，網絡拓撲B包含6個節點和7條邊。對于每個用戶請求，本文隨機從所有節點中選擇源節點sr和目標節點dr，并保證sr和dr不會重復。同時，假定用戶請求r的網絡流均分初始流量br。仿真參數如表2所示。其中，[X′,Y′]表示仿真參數隨機且均勻地從X′～Y′中生成，{I,J}表示仿真參數隨機地從I～J中生成(取整數)。另外，本文將單位時間間隔設定為1 s，為了研究單位時間間隔內用戶請求數N對設備負載的影響，本文將N設置成不同數值后進行仿真實驗。為了避免設定固定數值的時延約束lr對算法評估的負面影響，本文將時延約束lr設定為sr到dr的最短路徑時延和的2倍。

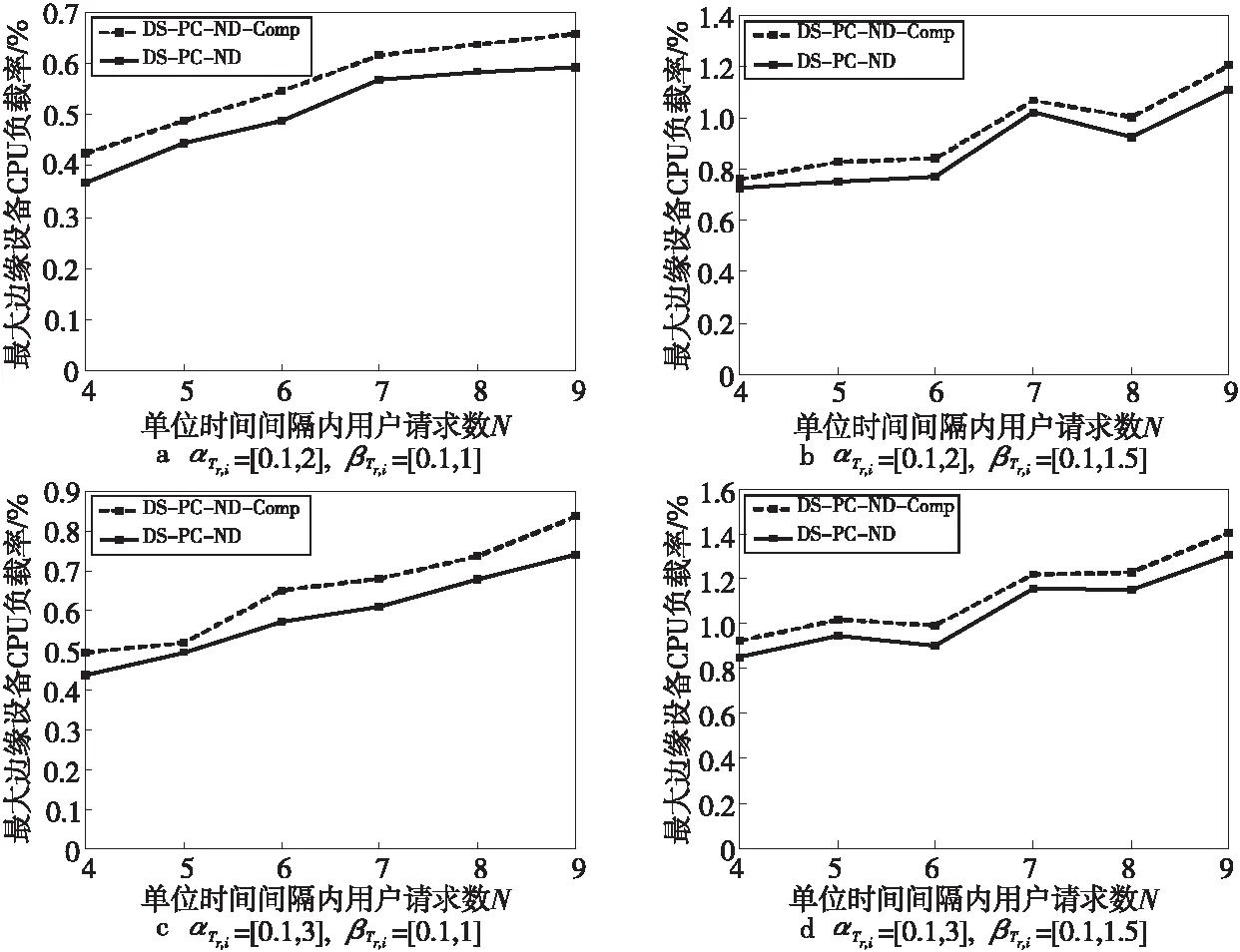
Figure 4 Comparison of DS-PC-ND and DS-PC-ND-Comp

5.2 評價指標

評估問題的目標函數為最大邊緣設備CPU負載率，即對最大的邊緣設備CPU負載進行歸一化后的結果。顯然，最大邊緣設備CPU負載率值越低，說明算法性能越好。

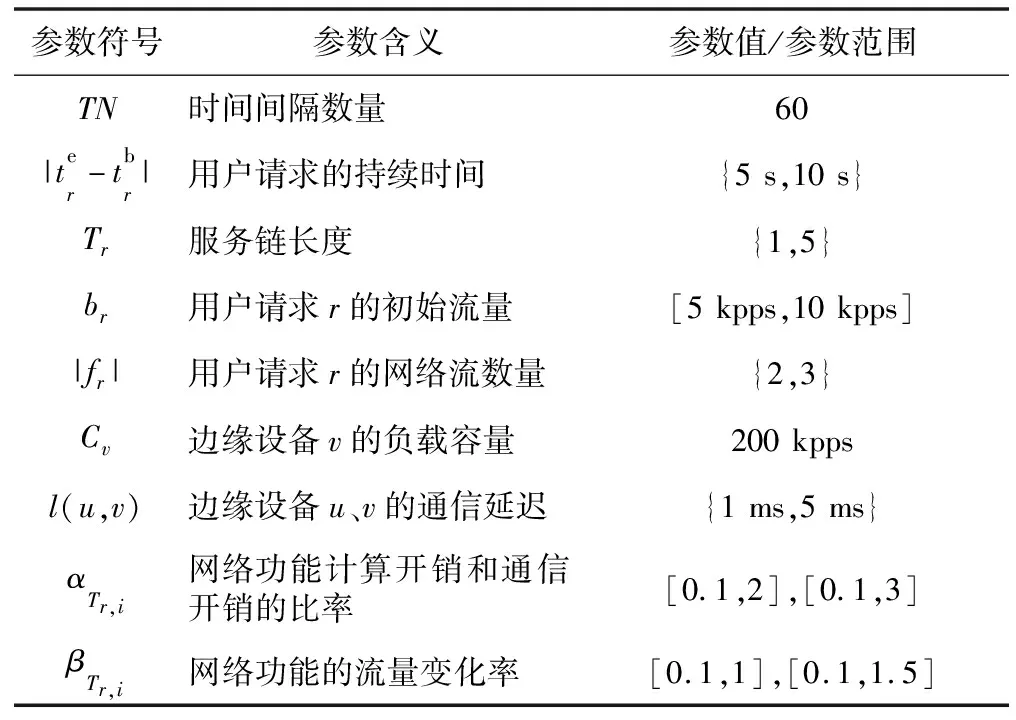
Table 2 Simulation parameter table

5.3 基準算法

基準算法DS-PC-ND-Comp是為驗證服務鏈網絡功能間通信開銷對邊緣設備負載均衡的影響而設計的。具體算法如下所示：保持DS-PC-ND算法框架不變，將服務鏈負載模型由服務鏈負載事實模型替換為服務鏈負載傳統模型，即認為服務鏈網絡功能間只存在計算開銷，并基于該認識去運行部署路徑選擇算法和網絡功能部署算法。

5.4 DS-PC-ND vs.DS-PC-ND-Comp

本節將評估DS-PC-ND算法相對于基準算法DS-PC-ND-Comp的優勢，以驗證忽略服務鏈網絡功能間存在通信開銷這一事實的不良影響，對比結果如圖4所示。可以看出，DS-PC-ND算法優于基準算法DS-PC-ND-Comp 3%～10%個單位邊緣設備CPU負載率。

更具體地說，圖4a和圖4b的βTr,i設置不同，這使得圖4b中通過網絡功能的流量可能變大，這增加了邊緣環境的流量總量，使得最大邊緣設備CPU負載率變大，同理可得圖4c和圖4d的結果對比；圖4a和圖4c的αTr,i設置不同，這增加了圖4c中服務鏈的計算開銷占比，使得最大邊緣設備CPU負載負載率變大，同理可得圖4b和圖4d的結果對比。

5.5 DS-PC-ND vs.Optimal

本節將評估DS-PC-ND算法和基于最優化方程求解的最優部署結果Optimal(使用規劃問題求解器Gurobi求解)的差距。為了降低求解最優部署結果的問題規模，本節將邊緣環境網絡拓撲修改為網絡拓撲B。在多個時間維度(TN=10,TN=20)下進行了仿真實驗，實驗結果如圖5所示。

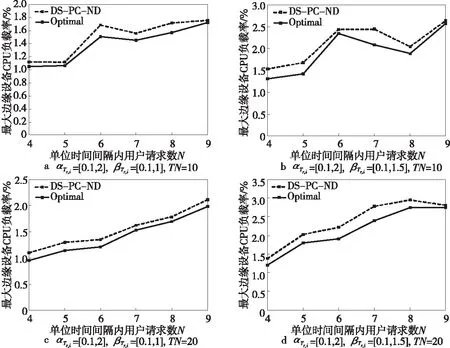
Figure 5 DS-PC-ND vs.Optimal

從圖5可以看出，DS-PC-ND算法的部署結果接近最優部署結果，這是由于部署路徑選擇算法盡可能選擇負載較小的部署路徑，而且網絡功能部署算法也盡可能地將網絡功能部署在負載較小的邊緣設備上，這些啟發式策略能保證接近最優部署結果。

6 結束語

在基于服務鏈網絡功能間存在通信開銷以及服務鏈網絡功能同時部署在多個虛擬實例內這2個事實基礎上，本文對面向邊緣環境的多實例服務鏈在線部署問題進行了建模，并提出了一個3階段算法DS-PC-ND進行求解。仿真實驗結果表明，該算法緩解了設備間的負載失衡現象，并且接近最優部署結果。由于該算法中包含啟發式算法，因此未來還有比較大的改進空間。