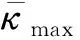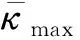軟體尺蠖爬行機器人建模與仿真分析

張力文， 徐齊平， 劉錦陽

(上海交通大學 工程力學系， 上海 200240)

不同于具有高剛度和復雜結構的傳統剛性機器人，軟體機器人具有結構簡單、人機交互安全性強、靈活性高、與復雜工作環境兼容性好的優點，是目前機器人行業中最具吸引力的領域之一.軟體機器人主要利用形狀記憶合金、橡膠材料、硅膠、介電彈性體及芳綸纖維等柔性材料制成[1-5]，能夠完成蠕動、游動、越障、跳躍及抓握等復雜的動作[6-10].其驅動方式主要包括流體驅動、形狀記憶合金驅動及電活性聚合物驅動等[11-13].

目前，軟體機器人的研究還處于起步階段，研究者們通常從自然界生物的外形結構和運動模式獲得靈感，設計適用于特殊環境作業的仿生機器人.Rafsanjani等[5]研制出了一種由硅橡膠管組成的蛇形機器人，當機器人充氣膨脹時，附著于機器人表面的可拉伸的塑料薄片會被迫彈出，從而錨定于地面上，整個機器人即可利用這些錨定的塑料片的拉動前進，這種蠕動爬行的運動方式為眾多仿蠕蟲和仿蛇的軟體爬行機器人的運動研究提供了新思路.王江北等[14]設計了一種多氣囊軟體爬行仿生機器人，通過對其硅膠材料的本構關系的研究，得出了機器人的運動步幅和內部氣壓的關系，并利用實驗驗證了該理論關系的可行性，為此類氣動驅動的軟體爬行機器人爬行步幅的實驗研究提供了理論指導.

在所有的仿生軟體爬行機器人中，尺蠖形四足軟體爬行機器人靈活性好、實用性強，是很多科研人員的重點研究對象.哈佛大學的Shepherd及其團隊對該類四足軟體爬行機器人進行了實驗研究，通過對機器人四肢上簡單的閥門系統進行充放氣控制，可實現四足之間的協調運動，從而能完成較為復雜的爬行動作[15].隨后，他們還利用高彈性硅膠材料制造出了抗干擾性更強的軟體機器人，該機器人由電動空氣壓縮機驅動，可以在嚴寒、炎熱等惡劣條件下長時間自主行進，并能抵抗高強度沖擊、碾壓等不利因素的干擾[16].雖然Shepherd及其團隊對四足軟體爬行機器人的結構、材料、運動步態以及適應能力進行了系統的研究，但是未對軟體機器人的建模進行深入研究.

氣動驅動的軟體機器人由多個氣腔構成，對其進行力學建模是一個復雜的過程.目前，對氣動驅動的軟體機器人的建模方法主要包括兩種：基于歐拉伯努利理論的曲梁建模方法和非線性有限元建模方法.加州大學伯克利分校的O’Reilly等[17-18]用曲梁建模方法對四足軟體爬行機器人運動時和地面的黏附情況進行了建模和理論分析，得出了與地面線接觸情況下軟體機器人運動的穩定性條件.隨后，他們還對于該類機器人和地面的摩擦接觸情況進行了分析，提出了一種能夠預測其運動方向的基于摩擦定律的彈性桿理論模型[19].文獻[20]還基于已經得出的穩定性條件和摩擦模型，將四足軟體爬行機器人的力學模型簡化為曲梁模型，對該類機器人的運動情況進行了理論上的建模和分析.然后，他們繼續通過實驗和理論推導，得出了四足軟體爬行機器人單個氣動致動器的曲率、彎矩以及內部壓強之間的關系，實驗上驗證了理論模型的正確性[21].此外，Majidi等[19]基于歐拉伯努利曲梁模型和庫倫摩擦理論建立了機器人運動方向和接觸面上摩擦力之間的理論關系.Matia等[22]采用基于歐拉伯努利梁模型估算了驅動的氣壓和變形之間的函數關系.Suzumori等[7,23]采用非線性有限元方法進行仿真計算，能夠得到相對準確的結果，但是計算時間較長，仿真效率較低.

以上學者對尺蠖四足軟體爬行機器人的運動提出了較為完善的理論模型，但是他們在研究過程中未考慮軟體機器人在不同運動階段之間的聯系，因此也未能反映機器人在整個運動周期內的連續變化情況.

本文針對軟體尺蠖爬行機器人建立了滑塊-曲梁的簡化模型，并對運動控制方程進行離散和無量綱化，利用牛頓迭代法求解準靜態條件的邊值問題.首先對軟體機器人在氣壓作用下的彎曲變形進行仿真，通過靜力學實驗驗證了理論模型的可行性，在此基礎上分析了軟體機器人在整個運動周期全過程中的姿態變化、行進運動規律情況.通過對所得結果進行詳細的討論和分析，得到軟體尺蠖機器人爬行運動的一般性規律，對于仿生爬行機器人的設計和運動分析具有一定的指導意義和價值.

1 軟體尺蠖爬行機器人的簡化力學模型

1.1 運動過程的描述

在初始狀態下對軟體尺蠖機器人充氣，可使其獲得一定大小的初始曲率，如圖1所示.本文利用具有初始曲率的曲梁表示機器人的彎曲構型，從而把整個軟體機器人簡化為由剛性滑塊和曲梁構成的簡化模型，稱之為軟體尺蠖機器人的滑塊-曲梁模型[8]，如圖2所示.圖中曲梁的線密度為ρ，滑塊的質量為ms，重力加速度為g，假設水平向右為E1方向，豎直向上為E2方向，建立整體坐標系OE1E2，原點O位于初始條件下滑塊與曲梁的連接處，且假設曲梁中線上任意一點沿E1方向和E2方向的坐標分別為x、y.

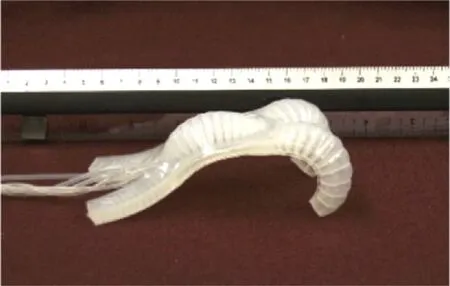
圖1 軟體尺蠖機器人Fig.1 Soft inchworm-like robot

圖2 滑塊-曲梁模型Fig.2 Slider-curved beam model

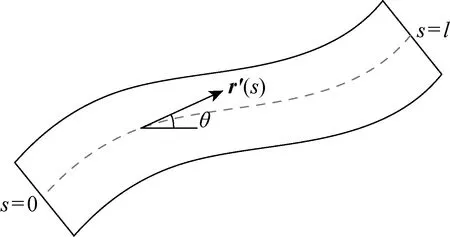
圖3 切向量r′(s)Fig.3 Tangential vector r′(s)

設曲梁中軸線上某一點距離其最左端處的弧長為s，曲梁總長度為l，該點處曲梁中軸線的切向量為r′(s)，如圖3所示.假設曲梁上處于0和s之間的任意一點的弧長為ξ，則切向量相對E1方向的姿態角θ為s的函數，其中，

(1)

設曲梁的初始曲率為κ0.根據 O’Reilly 的研究發現，初始曲率與氣腔內的氣壓成正比[21]，因此可通過控制κ0的變化對軟體機器人的運動進行控制.本文采用的κ0具有如下形式：

(2)

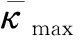
由于未知量的個數以及邊界條件的不同，將軟體尺蠖機器人在整個運動周期的運動狀況劃分為3個不同的階段，如圖4所示，圖中Δ為位移大小.

根據軟體機器人的實際運動狀況，其在一個周期內的3個不同階段的大致特征為：

(1) 階段C：機器人部分黏附于地面，隨著滑塊曲梁的初始曲率幅值從0逐漸開始增大，滑塊逐漸向右滑移，曲梁和地面的黏附部分長度也逐漸減少，即曲梁與地面逐漸剝離直到完全脫離，從而過渡到階段A.

(2) 階段A：機器人右端和地面點接觸，且該接觸點和滑塊都黏滯不動，隨著曲梁的初始曲率幅值減小，曲梁右端點處所需的摩擦力逐漸增大，該點逐漸產生向右滑移的趨勢.當曲梁的初始曲率幅值減小到一定值時，曲梁右端點開始滑移，從而過渡到階段B.

(3) 階段B：機器人右端仍然和地面點接觸，滑塊仍然處于黏滯狀態，但是曲梁的右端點會向右滑移，隨著曲梁的初始曲率幅值減小，該點逐漸向右移動直到初始曲率幅值減小到0，此時曲梁右端會開始貼附于地面，回到階段C.

可見，軟體尺蠖機器人完全可以通過上述3個不同階段之間的過渡和轉換，完成整個周期的運動，并向前滑移一段位移，實現連續向前爬行運動的目的.

1.2 應變能和重力勢能

不考慮曲梁模型的軸向變形，假設曲梁上任意一點的軸向應變為ε，軸向應力為σ，設曲梁截面彎矩為M，相應的抗彎剛度為EI(E為彈性模量，I為截面慣性矩).根據O’Reilly由實驗得出的結論，曲梁截面彎矩M和曲率的改變量存在線性關系[21]，此處可表示為M=EI(θ′-κ0).假設曲梁截面上任意一點相對中軸線上投影點的位置矢量在中軸線法向上的坐標分量為yu，以曲梁的體積V、截面積A以及弧長l′為積分自變量，由線彈性理論可以得到應變能為

(3)

當曲梁右端和地面點接觸時，若以曲梁左端點所在水平線為重力勢能的零點位置，在距離曲梁左端點長度為s處的豎直高度為Y(s)，重力加速度的大小為g，則整個曲梁的重力勢能WG為

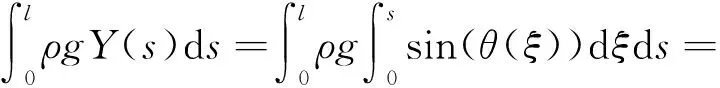
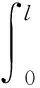
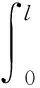
(4)

當曲梁和地面線接觸時，設γ為曲梁未黏附段的長度，h為慣性基原點相對于地面的高度，則曲梁上未黏附段的重力勢能WG1和黏附段的重力勢能WG2可分別表示為

(5)

1.3 外力勢能

當曲梁右端和地面點接觸時，設接觸點處支持力的大小為N1，摩擦力的大小為Ff1，并以沿著曲梁在左端點處為勢能零點，設FL=[Ff1N1]T，r(l)=[x(l)y(l)]T，此時由曲梁右端力產生的外力勢能為

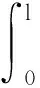
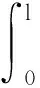
(6)

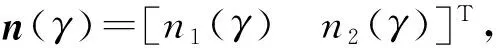
WF1=-n(γ)·r(γ).

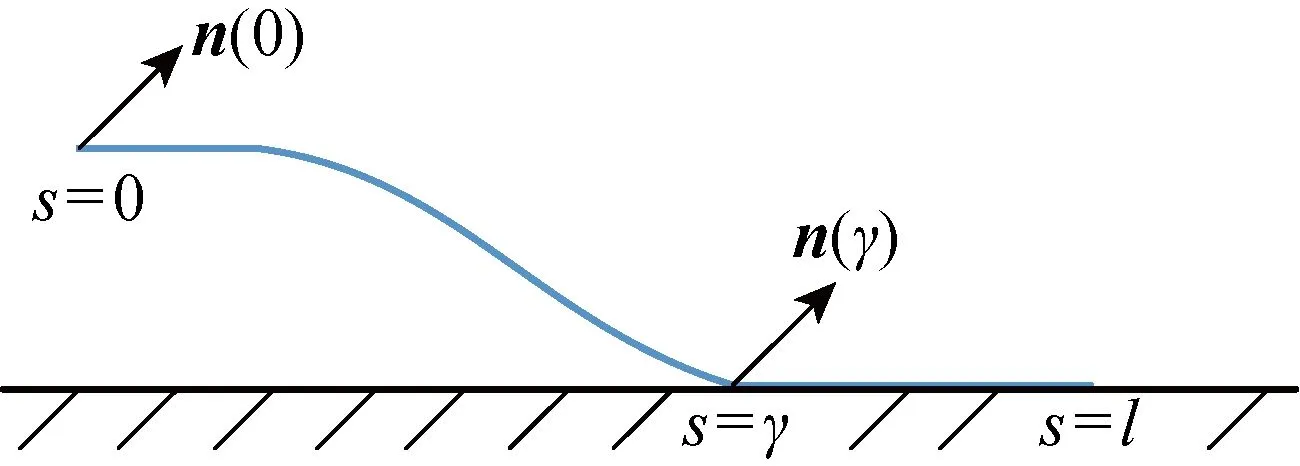
圖5 曲梁和地面線接觸時受外載荷的情況Fig.5 External force on curved beam when in line contact with the ground

1.4 控制方程的建立

當曲梁和地面點接觸時，結合曲梁的應變能、重力勢能以及外力勢能，可得到點接觸階段中曲梁的總勢能V1為

FL·r(l)=

(7)

當曲梁和地面線接觸時，曲梁的未黏附段的勢能V2為

(8)

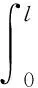
(9)

得到該情況下的控制方程的具體形式：

(Ff1sinθ-N1cosθ)=0,s∈[0,l]

(10)

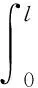
(n1(γ)sinθ-n2(γ)cosθ)=0,s∈[0,γ]

(11)

1.5 邊界條件的建立

對于階段A，曲梁和地面點接觸，由于曲梁左端和剛性滑塊固接，即θ(0)=0.由于曲梁右端為自由端，并且曲梁右端截面處也無外力矩，則此處的彎矩應該為0，可知M(l)=EI(θ′(l)-κ0(l))=0，即θ′(l)=κ0(l).

曲梁的左端點與滑塊固連，以該點為勢能零點，該點相對地面的高度為-h，且h>0，從而得到系統在豎直方向的幾何邊界條件：

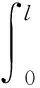
在曲梁右端點黏滯的階段A中，假設了曲梁右端點相對于滑塊黏滯，可設兩者間距離的大小始終保持為d，則有水平方向的幾何邊界條件：

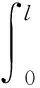
綜上，可聯立曲梁右端和地面點接觸時的控制方程以及邊界條件，階段A用于求解的滿足給定邊界條件的常微分方程組為

(12)

對于階段B，曲梁右端點滑移.設機器人與地面接觸點的靜摩擦因數和動摩擦因數分別為μs和μk，則可設曲梁右端處的水平速度為ν(l)>0，階段B在水平方向的邊界條件可寫為

此外，在準靜態條件下，設滑塊和曲梁的相互作用力沿E1和E2方向分量為n1和n2，對階段B中整個滑塊-曲梁系統進行靜平衡分析，如圖6所示，可以得到相應的靜力平衡方程N2=msg+ρgl-N1,Ff1=Ff2.階段B用于求解的滿足給定邊界條件的常微分方程組為：

(13)

如果|Ff2|>μsN2，曲梁左端點也發生滑移，Ff2=-μkN2.

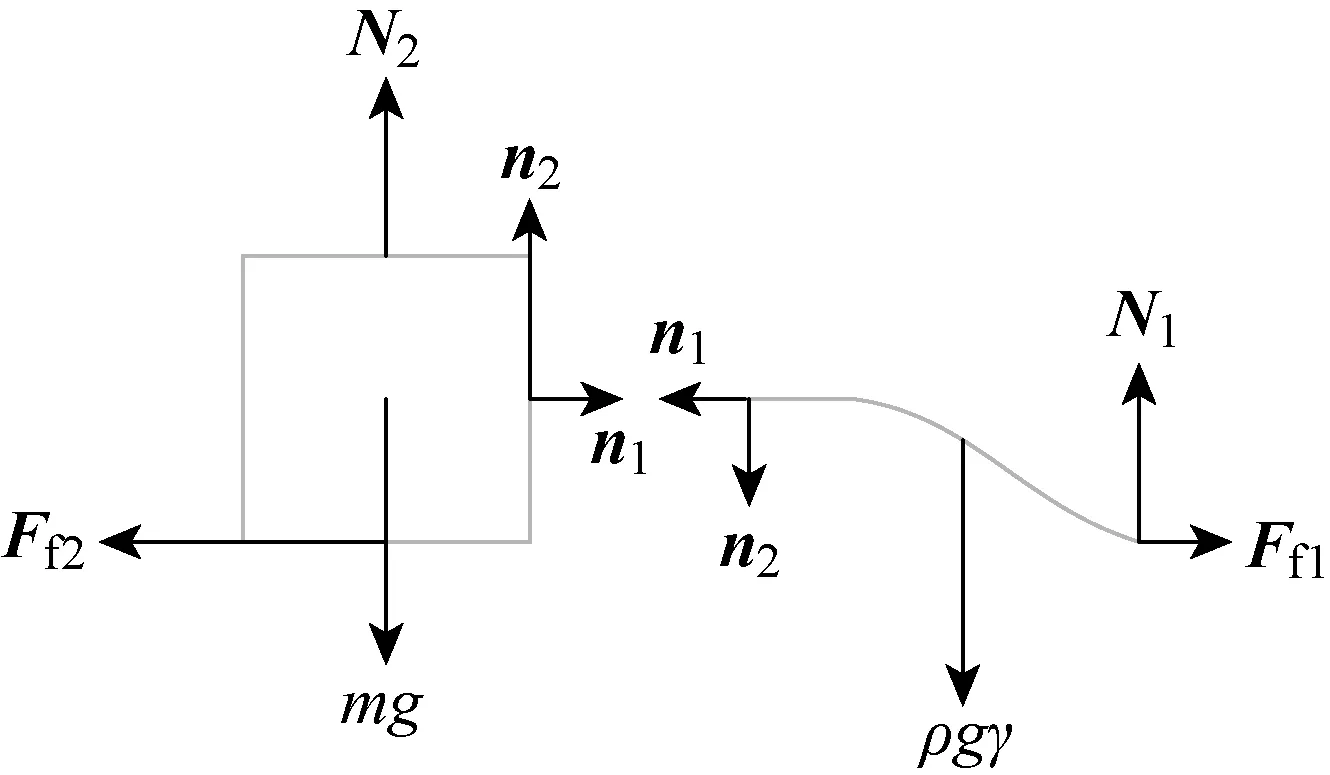
圖6 階段B中滑塊-曲梁系統的靜平衡分析Fig.6 Static equilibrium analysis of slider-curved beam system in phase B

對于階段C，在曲梁和地面線接觸的情況下，由于其在s=γ處的未黏附段右端點即為曲梁和地面接觸的起始點，則θ(γ)=0.此外，設滑塊和曲梁的相互作用力沿E1和E2方向分量為n1(0)和n2(0)，根據靜平衡條件先對滑塊進行力平衡分析，如圖7所示，得到如下關系式：

(14)

再對曲梁上未黏附段進行力平衡分析，如圖7所示：

(15)

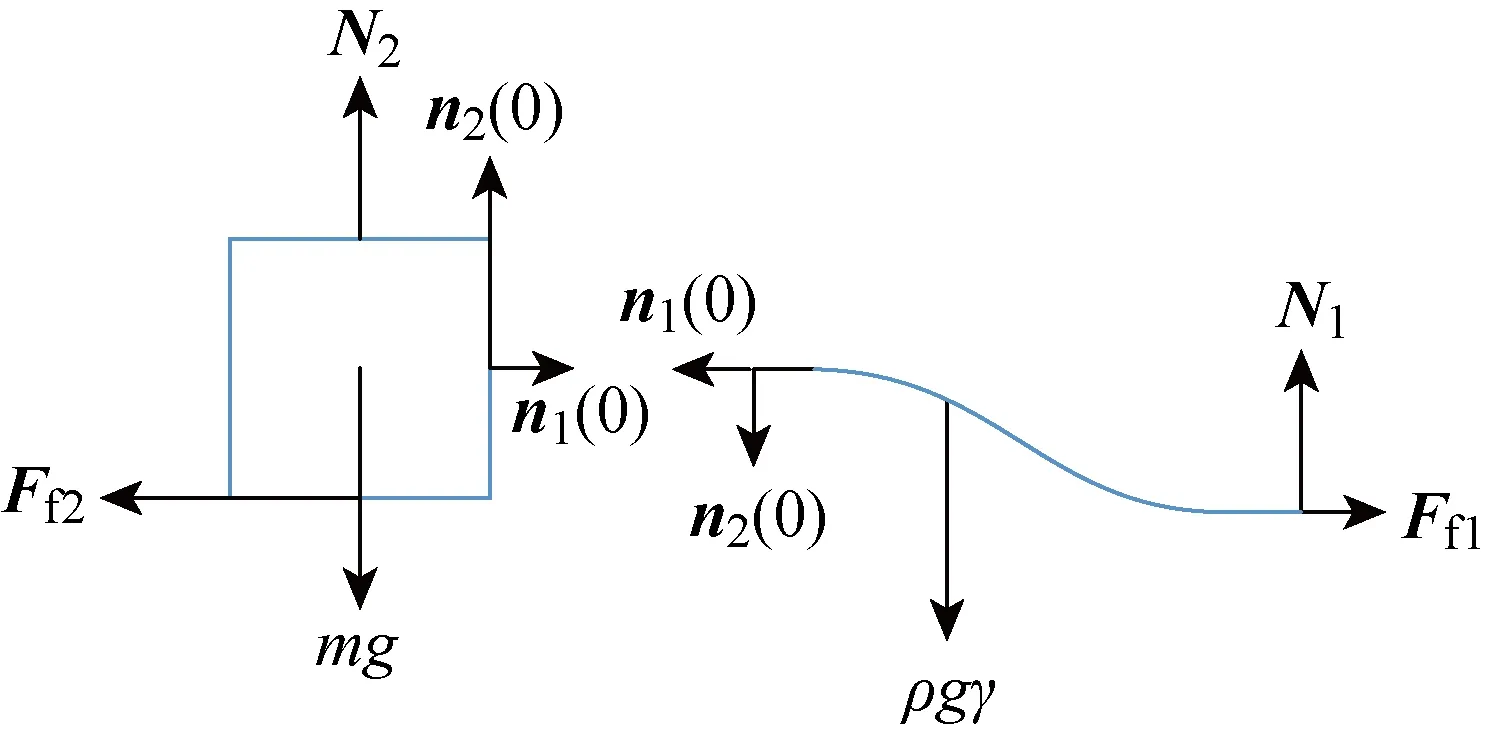
圖7 階段C中滑塊-曲梁系統的靜平衡分析Fig.7 Static equilibrium analysis of slider-curved beam system in phase C

由于滑塊在階段C情況下滑動，設滑塊處的水平速度為νh，動摩擦因數為μk，結合靜平衡方程得出的表達式，從而得到水平方向的邊界條件：

n1(γ)=μkN2sign(νh)=

μk(msg-n2(0))sign(νh)=

μk(msg+ρgγ-n2(γ))sign(νh)

(16)

式中：sign(νh)為符號函數，當νh≥0，sign(νh)=1；當νh=0，sign(νh)=0；當νh<0，sign(νh)=1.

當曲梁和地面線接觸時，還需要考慮由黏附作用產生的黏附勢能.設曲梁黏附段上單位長度的黏附勢能為-ω，曲梁未黏附段的黏附邊界條件為[17]

(17)

結合階段C的曲梁未黏附段的邊界條件和控制方程，則得到如下滿足給定邊界條件的常微分方程組：

(18)

2 軟體尺蠖爬行機器人控制方程的仿真分析

2.1 方程組的離散化和無量綱化

在曲梁和地面點接觸時，將連續的曲梁劃分為n段微段，如圖8所示，設其中每一微段的長度為ds，則nds=l.設第i段微段的左端點轉角為θi，則si=s(θi)=(i-1)ds.

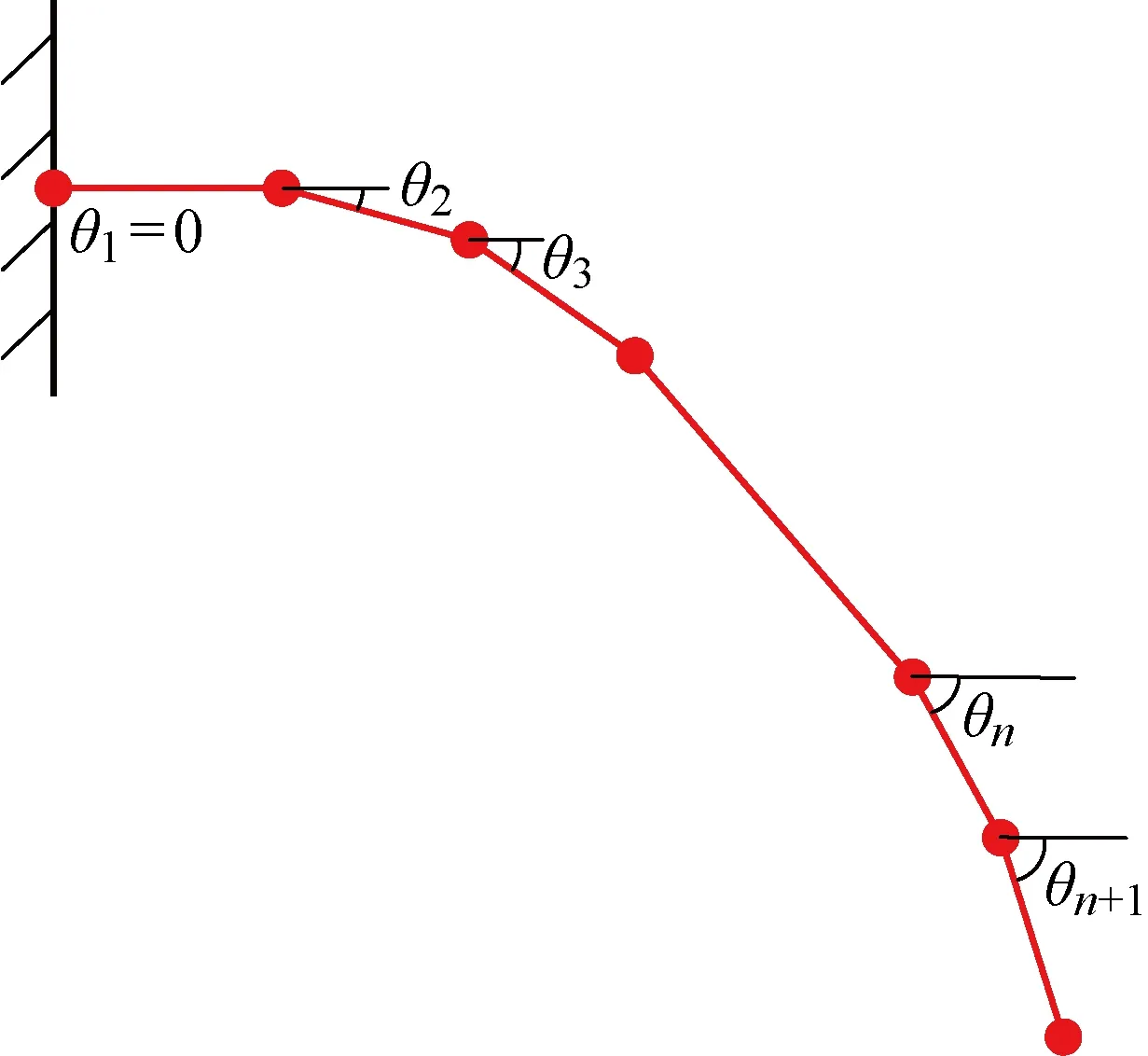
圖8 曲梁和地面點接觸時曲梁的離散構型Fig.8 Discrete configuration of curved beam when in point contact with the ground

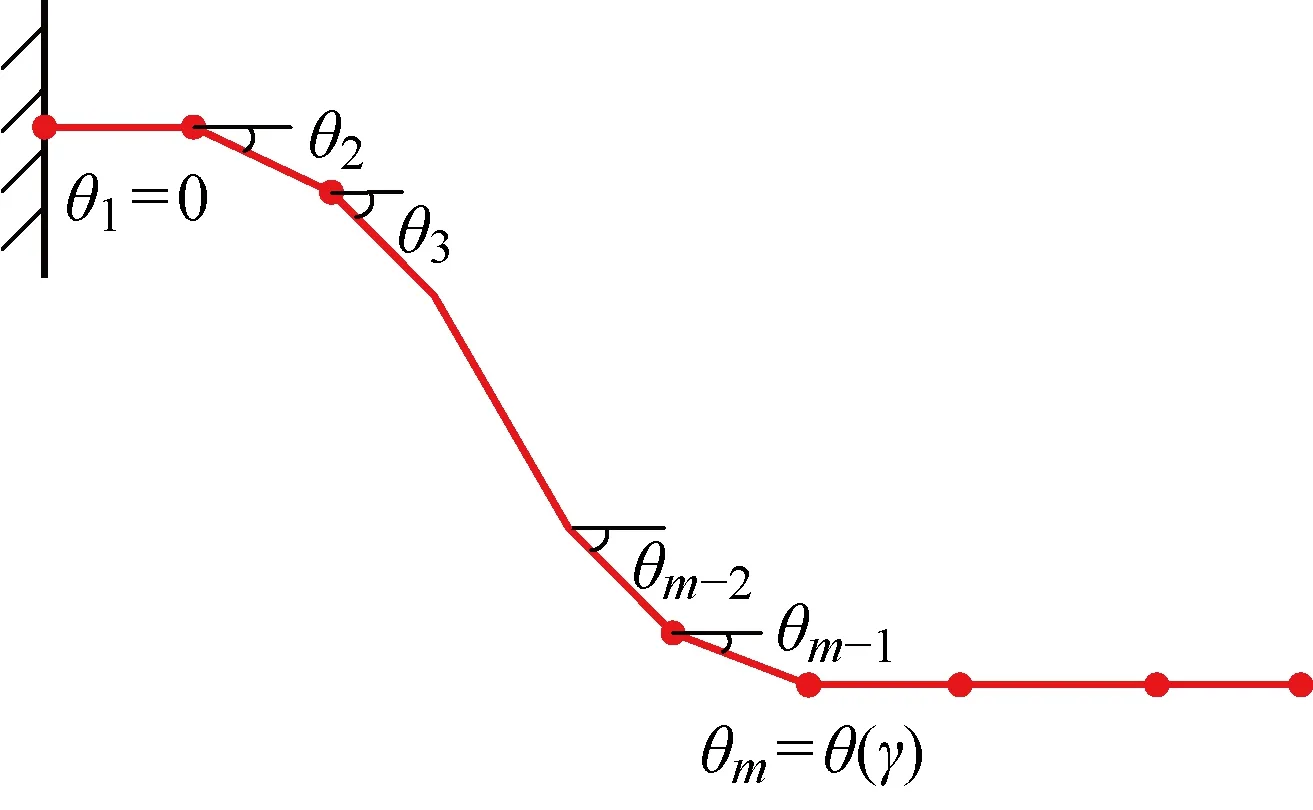
圖9 曲梁和地面線接觸時曲梁的離散構型Fig.9 Discrete configuration of curved beam when in line contact with the ground

假設曲梁右端末尾還存在第n+1段微段，該段長度仍為ds，且不納入曲梁的總長之中.則此時方程組的未知量共為n+3個，分別為θ1,θ2,…,θn,θn+1,N1,Ff1.

在曲梁和地面線接觸時，由于曲梁黏附段的構型已知，通過離散分析曲梁的未黏附段，完成在微段數目不變，微段長度改變的條件下曲梁構型的求解.將連續的曲梁未黏附段劃分為m段微段，每一微段的長度為ds，使得mds=γ，并且其他假設和點接觸階段相同.此時方程組的未知量個數共為m+4個，分別為θ1,θ2, …,θm,θm+1,n2(γ),n1(γ),γ.

本文中對所有的物理量都采取了無量綱化的處理，并將無量綱化的物理量做了新的符號規定，如表1所示.表中L′、F和T分別表示長度、力和時間的量綱.

從而可以寫出階段A最終的離散化、無量綱化的非線性代數方程組：

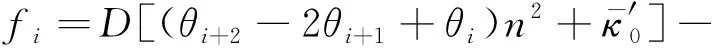
fn+2=θ1=0

同理，要寫出階段B的離散化、無量綱化的非線性代數方程組，只需采用如下fn+1替換上式中的水平方向邊界條件，即fn+1=Ff1+μkN1=0.

還可以寫出階段C最終的離散化、無量綱化的非線性代數方程組：

表1 各物理量的無量綱化Tab.1 Dimensionalization of physical quantities

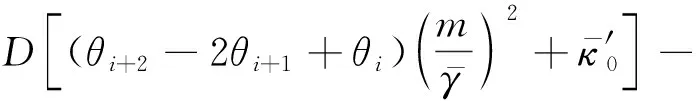
fm+1=θ1=0，fm+2=θm+1=0

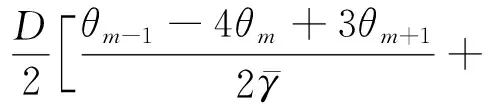
2.2 方程組的求解方法

此處將對牛頓迭代法的求解思路以曲梁和地面點接觸的情況為例進行說明，而曲梁和地面線接觸情況的求解過程與其一致.設方程組在第k次迭代時為列向量F(k)，此時由上一次迭代求得的未知量列向量為X(k)，求導結果構成維數為n+3的方陣即雅可比矩陣F′(k)，并設未知量迭代矩陣為H(k)：

H(k)=-F′(k)-1F(k)
X(k+1)=X(k)+H(k)

2.3 充氣變形的靜力學實驗

為了驗證p和κ0之間正比關系的有效性，本文進行了四氣腔軟體機器人充氣變形的靜力學實驗.將機器人的一端固定，研究其受不同氣壓載荷作用下的變形狀態，如圖10所示.

圖10 受不同氣壓載荷作用的軟體制動器的變形狀態Fig.10 Deformed states of soft actuator subject to different air pressure loads

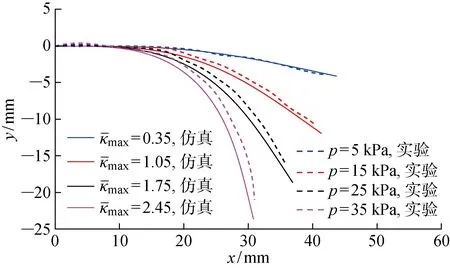
圖11 實驗和仿真得到的軟體制動器變形狀態的對比Fig.11 Comparisons of deformation state of soft actuator obtained by experiment and simulation

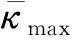
2.4 機器人運動姿態的準靜態實驗

為了驗證所建立的方程組求解結果的準確性，本文還通過準靜態實驗研究了長度為44 mm的單臂軟體機器人在爬行過程中某一個時刻的運動姿態，如圖12所示.單臂軟體機器人的特點是左端無姿態約束，滑塊的等效質量為0.

圖12 實驗過程中的軟體機器人Fig.12 Soft robot in experiment

在實驗過程中，隨著充放氣不斷交替變化，軟體爬行機器人逐漸向前運動，在不同的時刻產生了相應的變形形狀曲線，其中在時間t=2 s處軟體機器人的形狀如圖13所示.

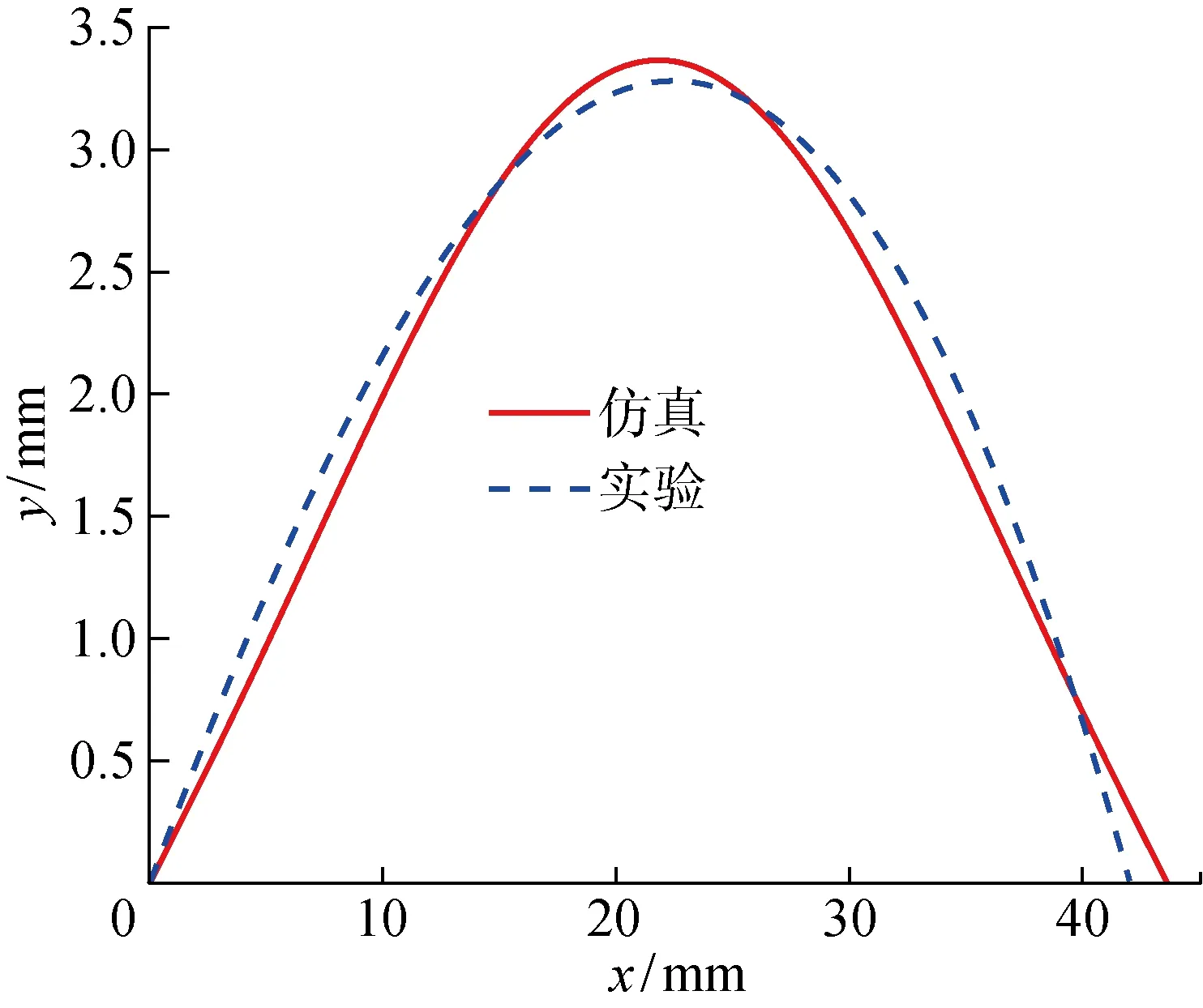
圖13 t=2 s時軟體機器人形狀的實驗和仿真結果Fig.13 Experimental and simulation results of soft robot shape at t=2 s

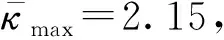
2.5 點接觸階段的計算結果分析

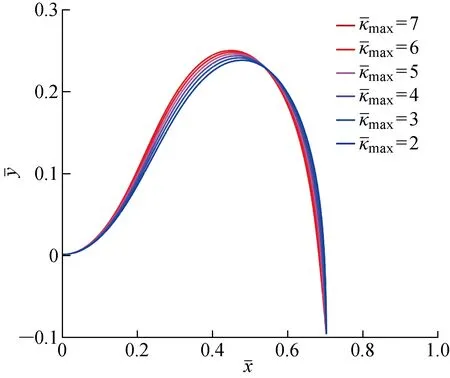
圖14 階段A在上的構型圖Fig.14 Configuration diagram in phase A at

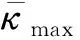
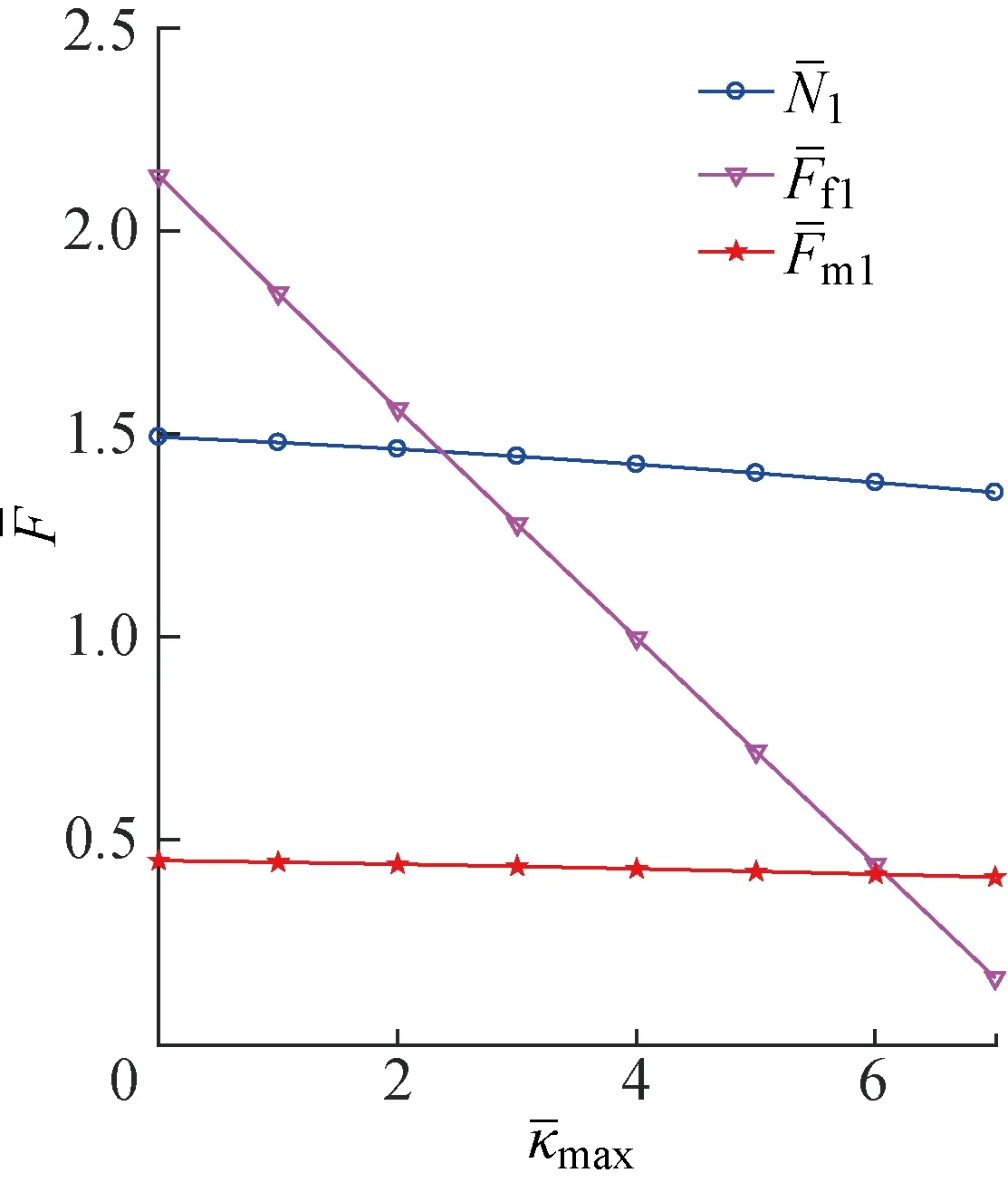
圖15 階段A中曲梁右端外力和的關系曲線Fig.15 External force of right end of curved beam versus in phase A

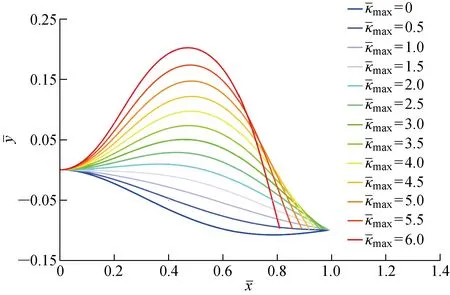
圖16 階段B在上的構型圖Fig.16 Configuration diagram in phase B at

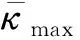
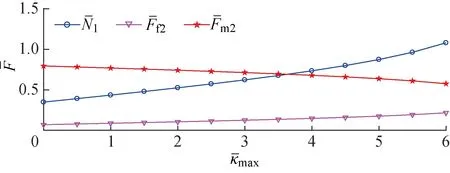
圖17 階段B中滑塊-曲梁系統外力絕對值和的關系曲線Fig.17 External force of slider-curved beam system versus in phase B

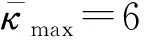
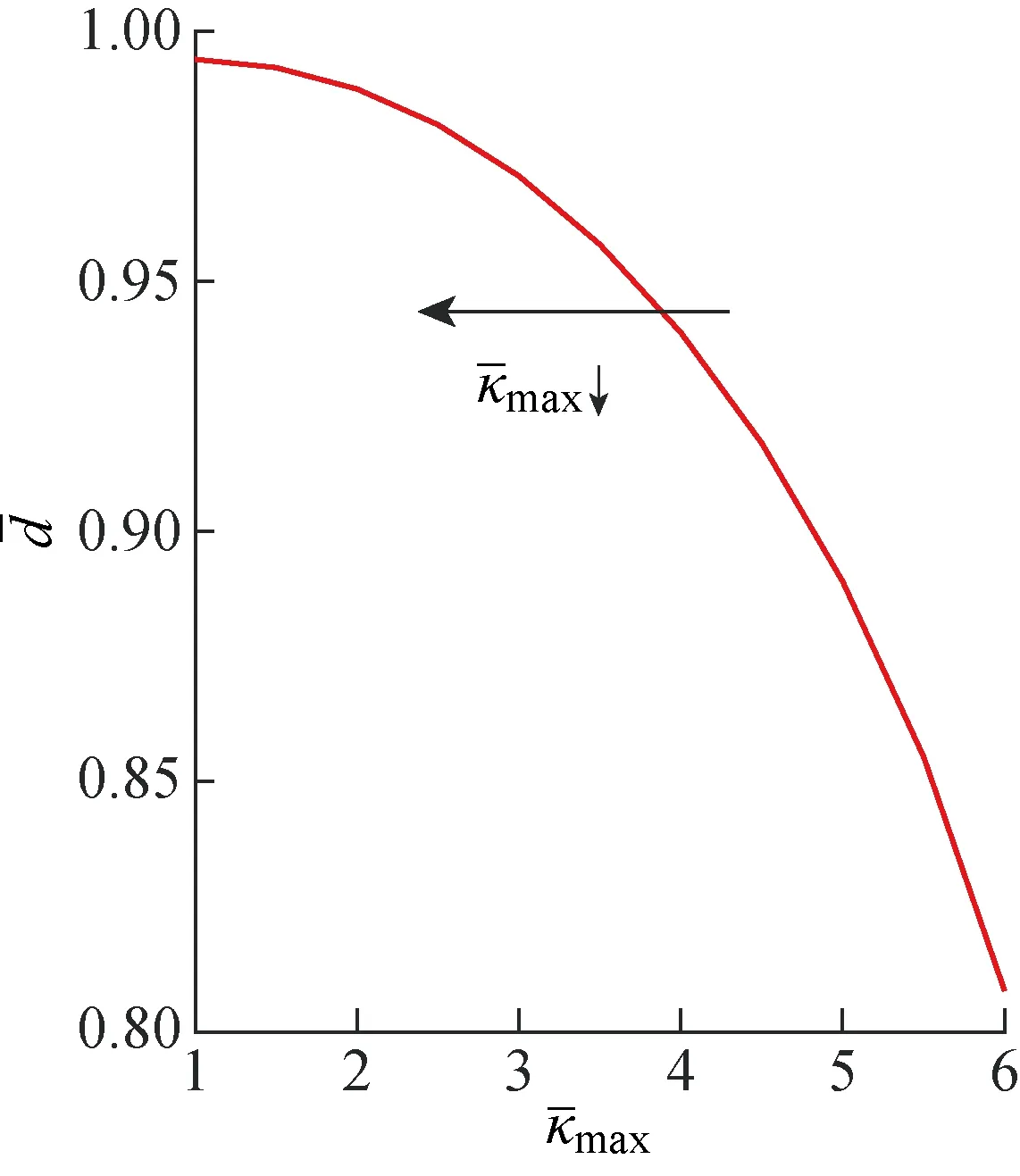
圖18 階段B中和的關系曲線 versus in phase B

2.6 線接觸階段的計算結果分析

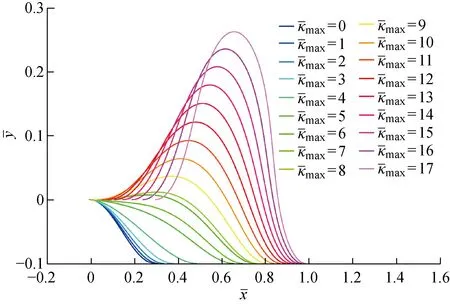
圖19 階段C在上的構型圖Fig.19 Configuration diagram in phase C at

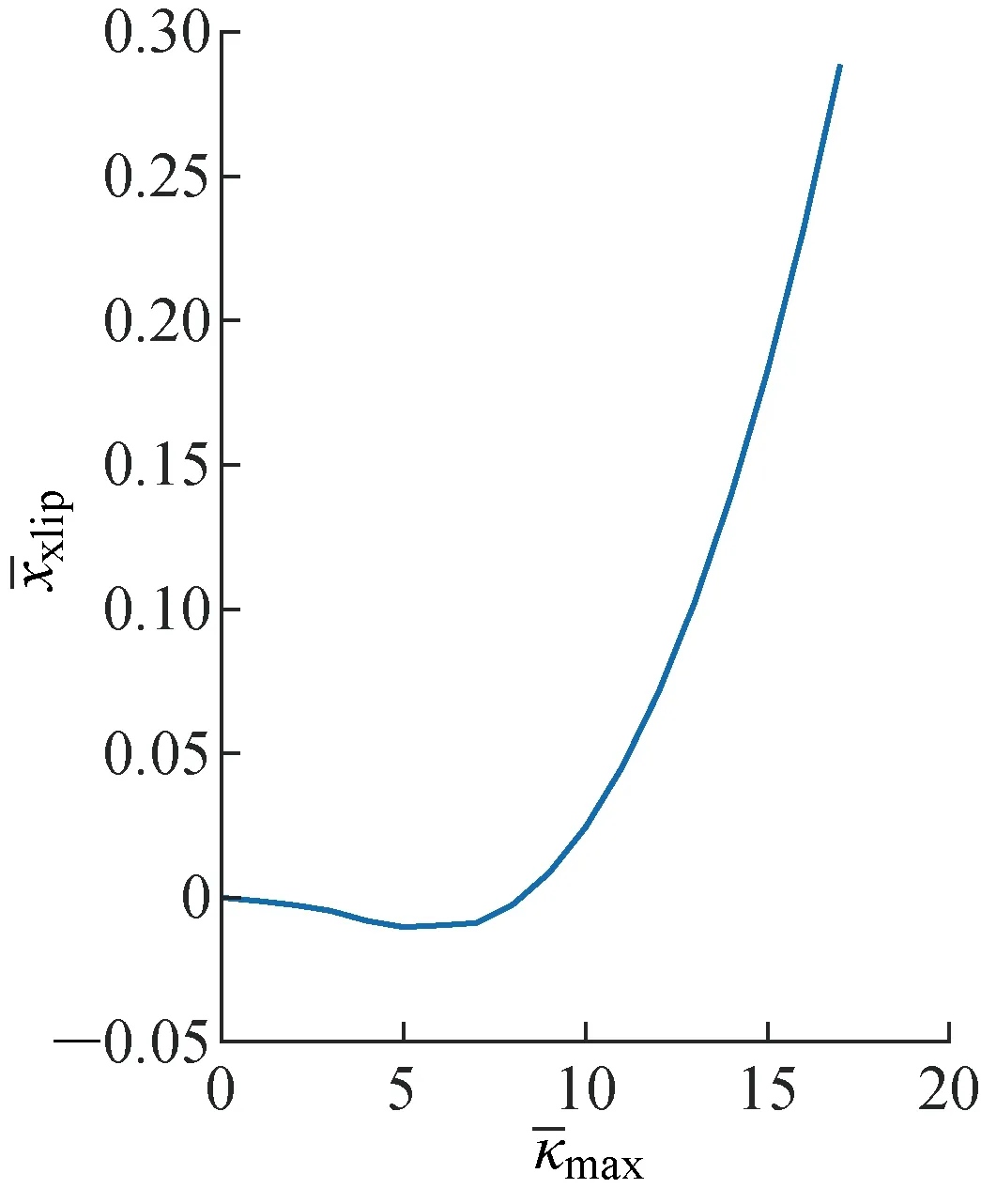
圖20 滑塊的位移和的關系曲線Fig.20 Slider displacement versus in phase C

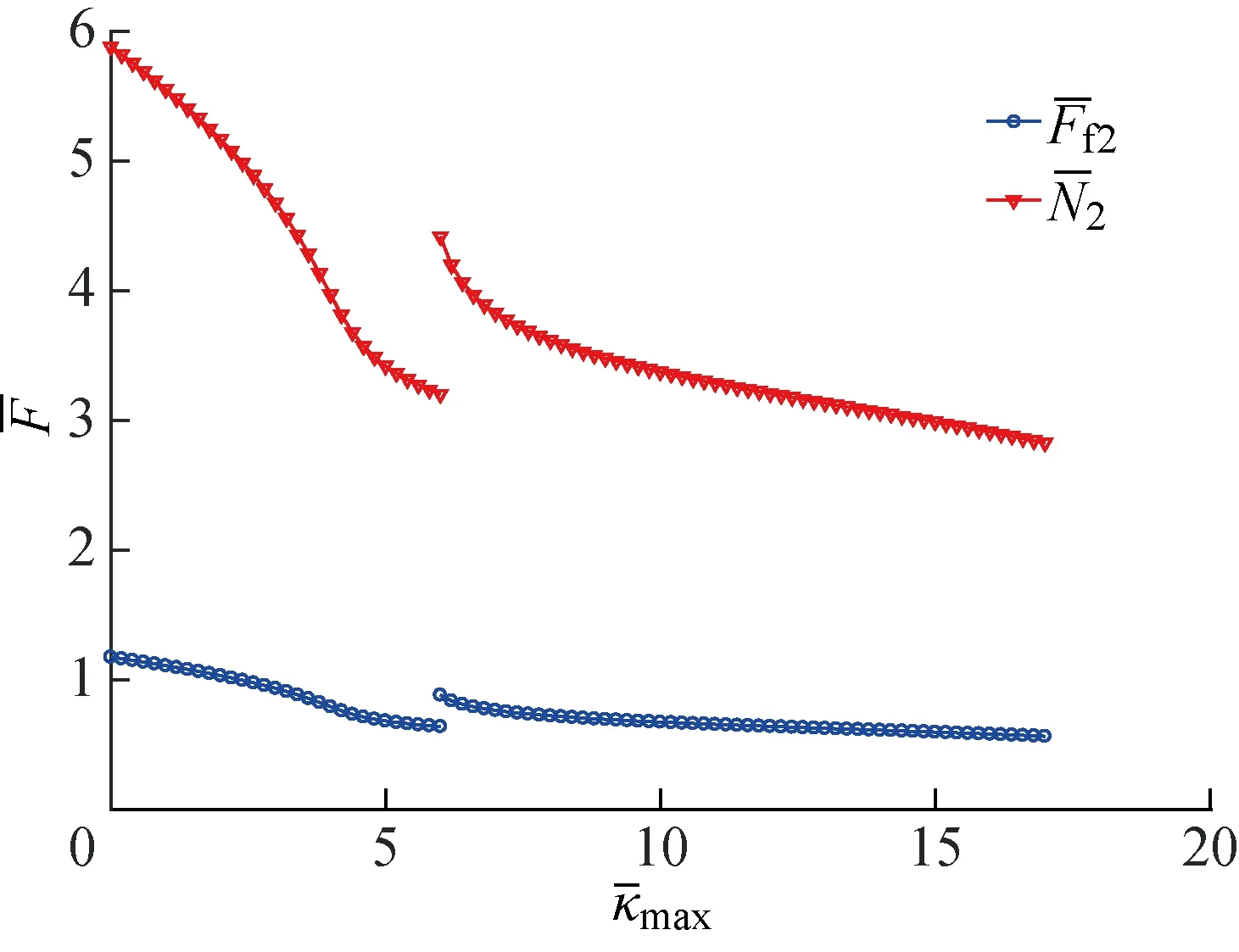
圖21 階段C中滑塊處外力絕對值和的關系曲線Fig.21 External force at the slider versus in phase C

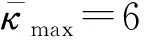
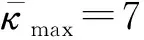
2.7 軟體尺蠖機器人的運動周期分析

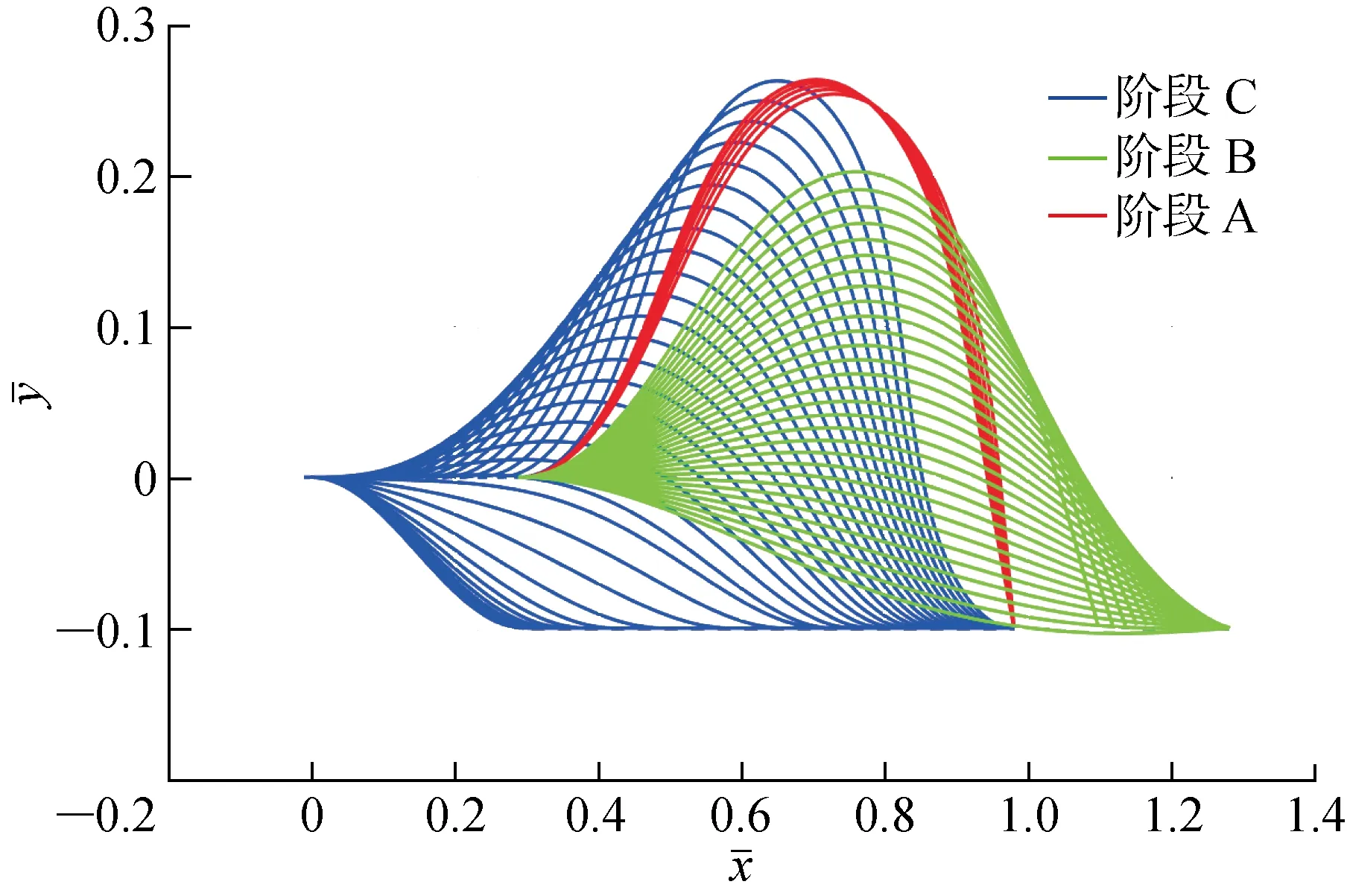
圖22 曲梁在整個運動周期內的構型變化Fig.22 Configuration changes of curved beams during the entire motion cycle

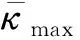
此外，若以階段C為起始階段，則也可以獲得初始時曲梁左右兩端點相對的水平位置距離.根據階段C的計算結果，曲梁的右端點在初始時的水平投影長度為 0.980 3l.而由階段B的計算結果，曲梁的水平投影長度在整個運動周期結束時為 0.990 5l，從而得知曲梁左右端點的水平距離在運動周期前后近似相等，意味著整個軟體機器人在完成了1個周期的運動后能大致回到運動前的構型和狀態，使得每個周期的運動過程近似一致，從而保證了本文的所有計算結果和分析結論對機器人在任意周期運動內的通用性、一致性.

3 結語

針對現有軟體爬行機器人的模型在模擬整體運動時的不連貫性、計算效率較低以及在整個周期內未能反映連續運動變化的情況，本文對軟體尺蠖爬行機器人建立了滑塊-曲梁的簡化力學模型，推導了用于數值求解的無量綱離散化的非線性代數方程組，對該機器人的整體運動狀況進行了準靜態建模和仿真分析.