充填體力學模型與穩定性分析

張博超，王少勇

(1.萊州市瑞海礦業有限公司， 山東 煙臺市 265309；2.北京科技大學 土木與資源工程學院， 北京 100083)

0 引言

傳統礦產資源開發過程中產生了大量的尾砂、廢石和廢渣等礦山固廢，造成地面塌陷，嚴重威脅礦區環境安全[1]。采用充填采礦法可實現礦山固廢的有效回填，基本消除地下采空區和地表尾礦庫，具有安全、環保和經濟的獨特優勢，已被廣泛應用于金屬礦、煤礦開采作業[2]。

當前，為提高充填效率，降低開采成本，對于充填過程控制與效果定量評價是充填采礦的研究熱點和難點[3-4]。對此，國內外學者已開展了大量研究工作，王海峰[5]利用 FLAC3D對采礦區地表變形及其充填效果進行了模擬分析，揭示了空區上覆巖層變形特征；傅國廷等[6]構建沿空留巷立體結構受力特征模型，并利用FLAC3D模擬了充填體寬度參數特征；孫曉光等[7]模擬了不同的充填體強度開采下層煤后的地表沉陷和頂底板彈塑性區分布；黃明清等[8]利用 FLAC2D優化空場嗣后充填法采場結構參數，對比分析了充填體的理想彈塑性本構模型及礦巖應變軟化本構模型。上述研究證實了FLAC3D在充填體分析的獨特優勢，但缺乏對充填體強度模型優化及其穩定性分析。

對此，本研究依托某銅礦的礦巖基本參數，構建了充填體自立強度模型，探究了充填體的力學特征及其影響機制，給出了充填體的應力狀態以及回采期間的穩定性規律，相關研究結果可為礦山實際開采與充填過程提供參考。

1 充填體力學與強度特征

1.1 自立強度模型

充填體的自立問題一直是充填技術的研究重點之一[4]。充填體要保持自立，必須依照相應的充填空間尺寸、圍巖條件而具備足夠的強度，使其不至沿揭露后的自由面垮落，此時的強度稱之為自立強度。1983年，Smith解除對充填體的約束，發現充填體典型破壞是剪切滑移破壞。據此，本文建立了充填體自立強度力學模型，如圖1所示。

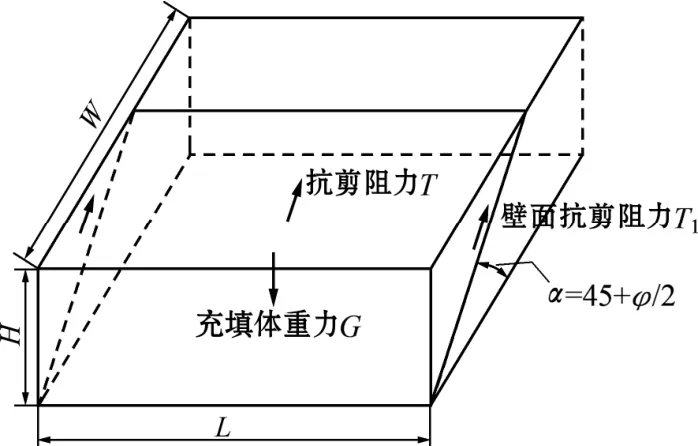
圖1 充填體自立模型

充填體自立條件是：滑動面上充填體重力分量G1小于滑動面的最大剪切力T與圍巖（或充填體）的壁面抗剪阻力T1之和，極限條件為相等，如式（1）與式（2）所示。

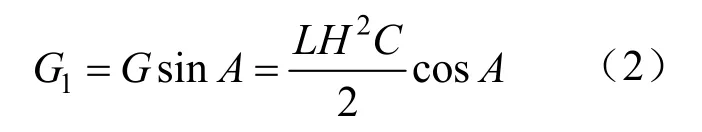
依據圖1力學模型進行計算，分別導出式（3）、式（4）各項，計算得到充填體自立強度Rv：

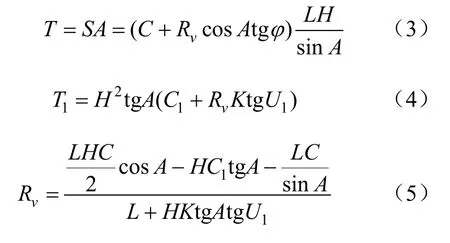
式中，Rv為充填體自立強度，MPa；L為充填體長度，m；H為充填體高，m；C為充填體黏結強度，MPa；φ為充填體內摩擦角，（°）；A為充填材料坍塌角，（°），A=45°+φ/2；K為側壓系數；U1為礦體內摩擦角，（°）；C1為礦體黏結強度，MPa。

1.2 充填體強度確定

基于RMR和Q系統對地下礦巖的穩定性進行分析，上盤圍巖與礦體均屬于Ⅱ級，巖體質量良好。下盤圍巖屬于Ⅲ級，巖體質量中等。

充填體暴露寬度為15 m，長度為35 m，暴露高度根據不同開采及充填方案有4種：4 m，5 m，6 m，50 m。不同的理論計算模型，可獲得不同采高充填體強度值，見表1。其中，側壓系數K=1-sinφ，取0.34，坍塌角A=65.75°。

對比表1，結合各礦山采用的充填強度值，確定實驗礦山充填體強度范圍為1.5 MPa～2.5 MPa。當灰砂比為 1:4，充填濃度為 74%時，充填體強度為2.2 MPa，可滿足分層開采高度為4～6 m時的充填體強度要求。

2 模型建立與邊界條件

2.1 基本假設

表1 不同理論模型下充填體強度計算結果

由于礦山地質結構的復雜性，影響采場穩定因素的多樣性，為保證計算結果可靠性，在模型建立和計算過程中采用以下簡化和假設：

（1）階段運輸巷道、天井、人行材料井等工程對采場的穩定性影響很小，因此，本次研究不考慮這些工程對采場穩定性的影響；

（2）假設模型中的巖體和充填體均為各向同性的連續介質；

（3）在建模中忽略模擬范圍內的節理、裂隙和斷層；

（4）在模擬計算中，忽略爆破震動、地震波及地下水對圍巖穩定性的影響，僅考慮重力對模型的影響。

2.2 模擬參數確定

巖體力學參數主要有抗壓強度、彈性模量、抗剪強度、抗拉強度和泊松比等，為獲得與現場實際相近的巖體力學參數，可采用多種方法對獲得的巖石力學參數進行弱化。巖石的物理力學參數見表2。

結合巖石物理力學參數與相關文獻資料選取充填體物理力學參數，見表3。

2.3 物理模型獲取

依據研究需求，物理模型所選取的尺寸為采場高度、寬度和長度的 3～5倍。模型建立并劃分網格，以垂直礦體走向為X軸方向，沿礦體走向為Y軸方向，模型的高為Z軸方向，分別建立了上、下盤圍巖和礦體模型，整體模型的尺寸為292 m×87m×250 m，如圖2所示。

表2 內蒙某銅礦巖石物理力學參數

表3 充填體物理力學參數

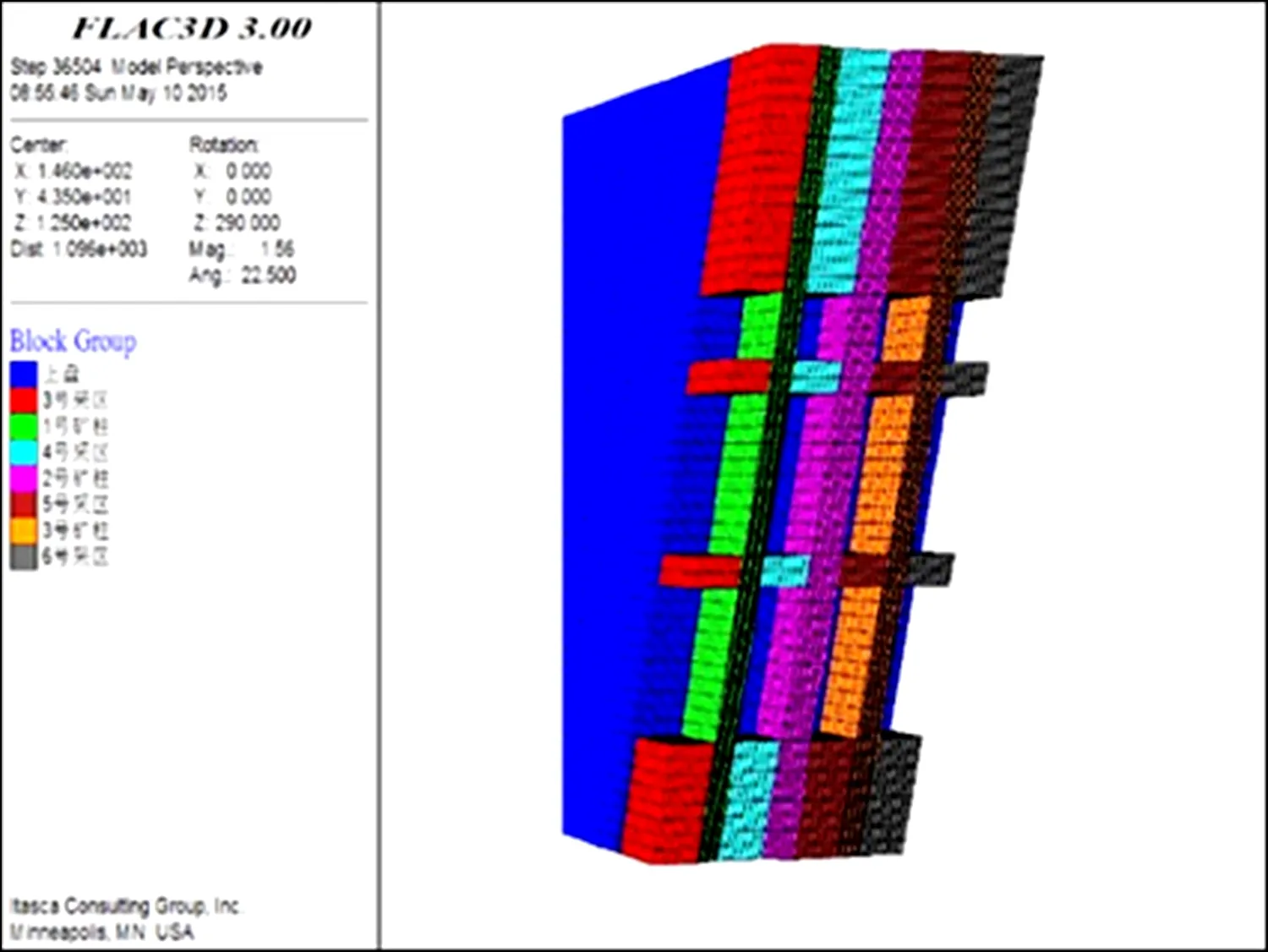
圖2 基于FLAC3D的物理模型

2.4 計算破壞準則

礦體上、下盤圍巖均為侏羅系上統白音高老組上安山質凝灰巖，圍巖蝕變較強烈，顏色為淺灰-深灰色，表現為綠泥石化、絹云母化、黃鐵礦化及高嶺土化，受構造的影響局部出現片理狀，礦體與圍巖界線呈漸變關系，總體走向與地層基本一致，適用莫爾-庫倫破壞準則，在數值計算中選用了莫爾-庫倫破壞準則進行模擬，如式（6）所示。

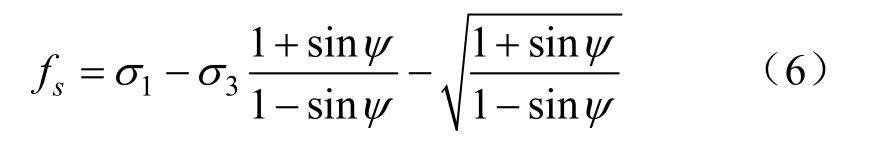
式中，σ1為巖體最大主應力，MPa；σ3為巖體最小主應力，MPa；ψ為巖體內摩擦角，（°）。

3 模擬結果與穩定性分析

3.1 不同強度要求下充填體力學行為分析

充分考慮充填體與圍巖之間的力學關系，在理論計算結果的基礎上，分別選取充填體抗壓強度值為：1.7 MPa和2.2 MPa，分層回采充填高度為4 m。利用FLAC3D數值模擬軟件，分析不同礦柱回采充填體強度特征，如圖3所示。

由圖3可知，3個礦柱同時回采時豎直向上的最大位移出現在采空區底部，在1.7 MPa條件下，其最大位移值約為3.62 cm，位移場相對穩定；在2.2 MPa條件下，最大位移同樣出現在底部，最大位移值約為21.2 cm，拉應力區域減小了50%，塑性發展區體積由62 865 m3降至40 722 m3。因此，充填體強度值在1.7 MPa以上，分層回采充填高度4 m的條件都是可行的，但充填體強度2.2 MPa比1.7 MPa更加能夠保證礦柱回采時充填體的穩定性。

3.2 不同分層回采充填高度下充填體強度特征

本研究選取4 m，5 m，6 m和20 m作為礦柱分層回采充填的高度，其應力場、位移場和充填體塑性區分布，充填體強度值選擇為2.2 MPa，充填體塑性區分布如圖4所示。

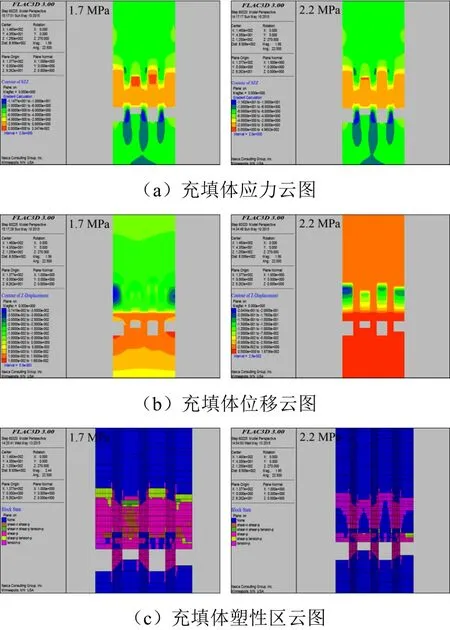
圖3 不同強度要求下充填體強度特征

由于回采，采場及附近圍巖應力明顯釋放，圍巖應力場重新分布，礦柱的頂部和底部出現了壓應力集中區。由圖4（a）可見，采場周邊圍巖的位移分布基本呈對稱狀態，3個礦柱同時充填時位移場穩定，充填效果較好；由圖4（b）可見，充填體底部右側始終產生向上的位移，且隨著開挖和充填步驟的增多，其位移等值拱的拱徑逐漸變小；由圖4（c）可見，3個礦柱同時回采，采場中充填體的塑性區體積由62 865 m3降至為40 722 m3，剪應力主要出現在礦柱回采后，兩側的充填體上，塑性區并未貫通。塑性發展區體積由40 722 m3降低至26 776 m3，礦柱回采后充填體與采場中充填體之間剪應力和拉應力減少；此外，由圖4（d）可見，4個采場頂部均出現了拉應力，其值為0.33 MPa，拉應力的出現不利于結構的穩定性。

3.3 充填體位移與塑性變形分析

當采用一次回采、充填體強度為2.2 MPa時，其對周邊采場的充填體將會產生較大影響，其應力、位移、塑性區分布如圖5所示。

由圖5可見，一次回采50 m的最大主應力值是其他3種回采形式最大主應力值的2～3倍；此外，豎向位移數值沒有增大，但頂部的下向位移、底部的上向位移范圍增大很多，表明易變形區域增大；由圖5（c）可見，該充填體目前正處于塑性變化過程中，出現了剪切破壞塑性區，因此，礦柱采用50 m一次回采會導致采場充填體整體失穩。

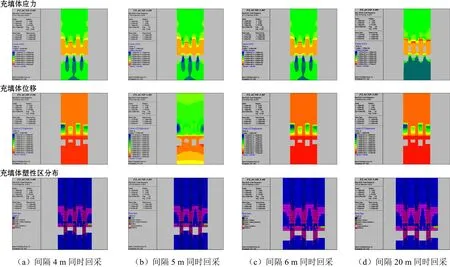
圖4 不同分層回采充填高度下充填體強度特征分布

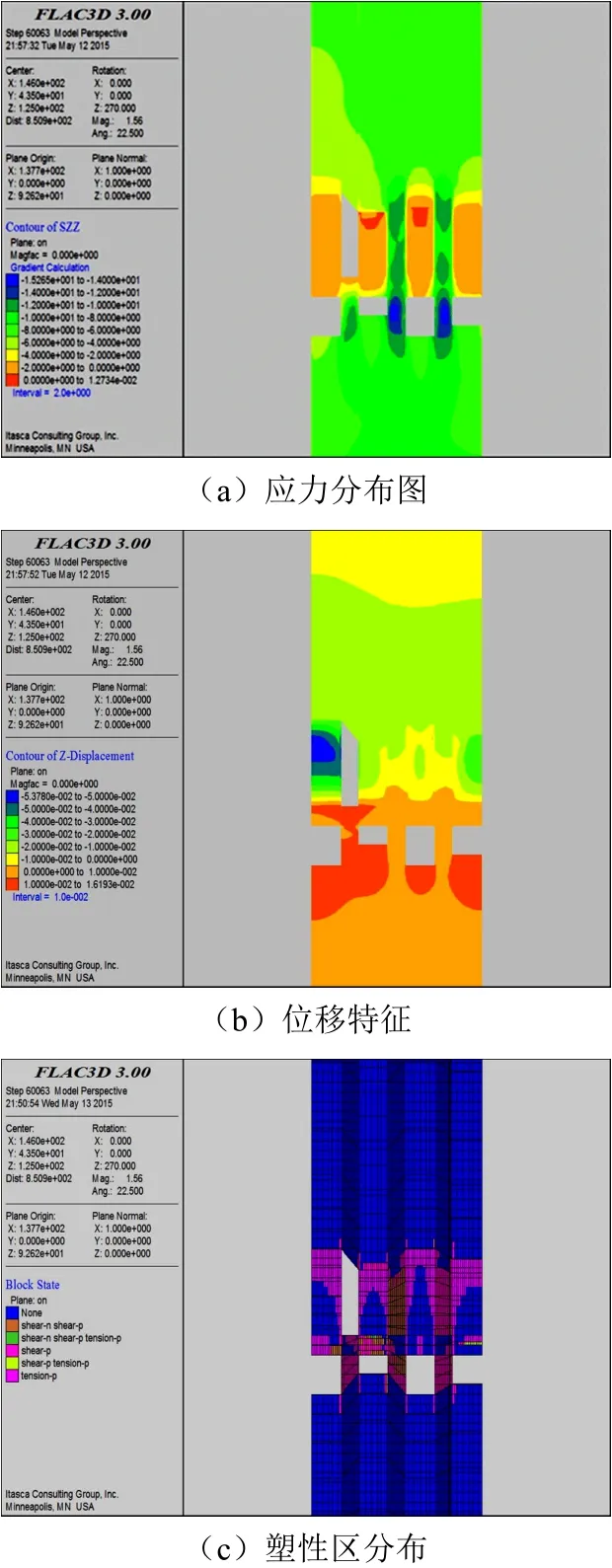
圖5 10 MPa充填體礦柱回采高度50 m

3.4 充填體對采場底板的應力作用分析

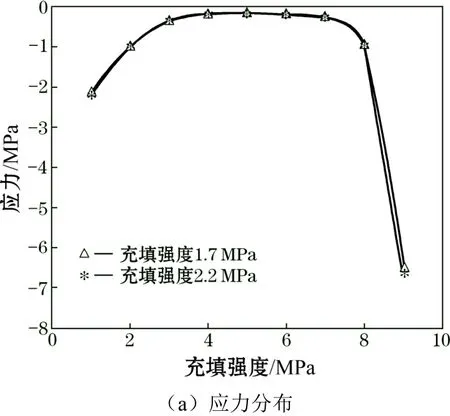
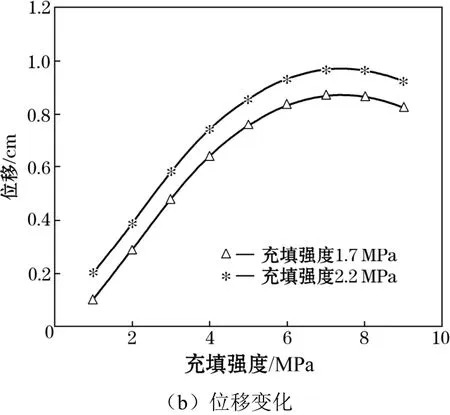
若充填體對其底板的應力較大，也會對下一中段的頂板產生影響，因此，將充填體底部的最大主應力數據提取繪制成圖，如圖6所示。

由圖6可見，2.2 MPa的充填體相比1.7 MPa的充填體對底板的影響較小，但在與圍巖接觸的兩側會對下一中段頂柱產生影響，從圖6可見，當充填體強度為2.2 MPa時，產生的豎向變形較小，最大豎向位移僅約為1 cm，因此，預留10 m礦體作為頂柱是可行的。

4 結論

（1）依據充填體自立強度模型，獲得最適充填體強度范圍為1.5 MPa～2.5 MPa，綜合考慮采場內三角礦堆與最上層充填體回采作業要求，建議最下分層與最上分層充填體強度為2.2 MPa；

（2）采用50 m嗣后充填方案時，2.2 MPa的充填體不會發生破壞，但礦柱應力集中顯現明顯，達到15 MPa，回采風險較高；

（3）當充填體強度為2.2 MPa時，產生的豎向變形較小，最大豎向位移僅為1 cm左右，因此預留10 m礦體作為頂柱是可行的。