礦用鋼絲繩損傷檢測信號處理方法研究

王紅堯， 吳佳奇， 李長恒， 唐文錦， 張艷林

(1.中國礦業大學(北京) 機電與信息工程學院， 北京 100083;2.華北科技學院 河北省礦山設備安全監測重點實驗室， 河北 廊坊 065201)

0 引言

鋼絲繩因具有彈性好、承載能力和耐用性強等特點，廣泛應用于煤礦主副井提升系統、單軌吊機車運輸系統、架空乘人裝置等。因工作環境惡劣，礦用鋼絲繩在長期使用過程中不可避免地會產生損傷，存在安全隱患。《煤礦安全規程》規定，必須對鋼絲繩進行定期檢測與維護。

電磁檢測法是目前最常用的礦用鋼絲繩損傷檢測方法。在實際應用中，受工作環境、繩股效應、斷絲頭沖擊等[1]因素的影響，鋼絲繩損傷電磁檢測信號中包含大量噪聲，且存在尖峰和突變干擾，使表征損傷的波峰和波谷(即信號奇異部分)無法清晰顯示，增大了損傷信號定性和定量識別難度。為了提高損傷檢測的準確度，需要對檢測信號進行處理，降低噪聲干擾。目前常用的鋼絲繩信號處理方法有傅里葉變換、小波變換等。傅里葉變換借助正弦波分解原始信號并分析信號頻譜，但無法反映信號瞬時頻率隨時間的變化情況，僅適用于分析平穩信號，無法對非平穩信號的特定成分進行降噪處理。小波變換[2-4]可對鋼絲繩損傷檢測信號進行多尺度分解重構、濾波、去噪處理，也可對檢測信號進行壓縮和傳遞，具有多分辨率、基小波選擇靈活、可多尺度分析等特點，但存在平移不變性較差、頻帶混疊等問題，導致在鋼絲繩檢測信號分解、重構過程中引入股波噪聲，影響檢測準確度。

雙樹復小波變換是N.G. Kingsbury提出的一種信號處理方法[5]，解決了小波變換中平移不變性較差、頻帶混疊等問題[6]，可使信號中的奇異部分更加清晰，有利于提高檢測準確度，在圖像壓縮、去噪等方面已有應用，尚未有用于礦用鋼絲繩損傷檢測的報道。本文提出一種基于雙樹復小波變換的礦用鋼絲繩損傷檢測信號處理方法，以消除檢測信號中的噪聲，提高后續損傷特征提取與識別的準確度。

1 雙樹復小波變換理論

雙樹復小波變換是基于小波變換形式的復數小波變換。其通過設計2個小波濾波器組，建立雙線并行的小波變換樹(即實部樹和虛部樹)對信號進行小波分解。為了實現實部樹和虛部樹的小波分解系數互補，將虛部樹的采樣位置設置在實部樹的中點，使2種系數可被有效利用，從而彌補了小波變換平移不變性缺陷，同時提高了計算效率[7]。

雙樹復小波變換采用小波變換中的1/2頻程轉換公式。在雙樹復小波變換應用于實際工程中時，可根據實際需求選用奇偶濾波器構造法、共同因子法和Q平移法構造高低通濾波器，以此進行信號分解和重構。針對礦用鋼絲繩損傷檢測信號，若采用奇偶濾波器構造法、共同因子法構造雙樹復小波變換的高低通濾波器，則只能在很小的范圍內具有線性相位，而采用Q平移法時，在雙樹復小波變換中每一層虛部樹的采樣位置恰好位于實部樹采樣位置的中點，具有很強的對稱性，對鋼絲繩損傷檢測信號降噪和特征提取非常有利[8]，因此本文選用Q平移法構造雙樹復小波變換濾波器。

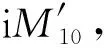
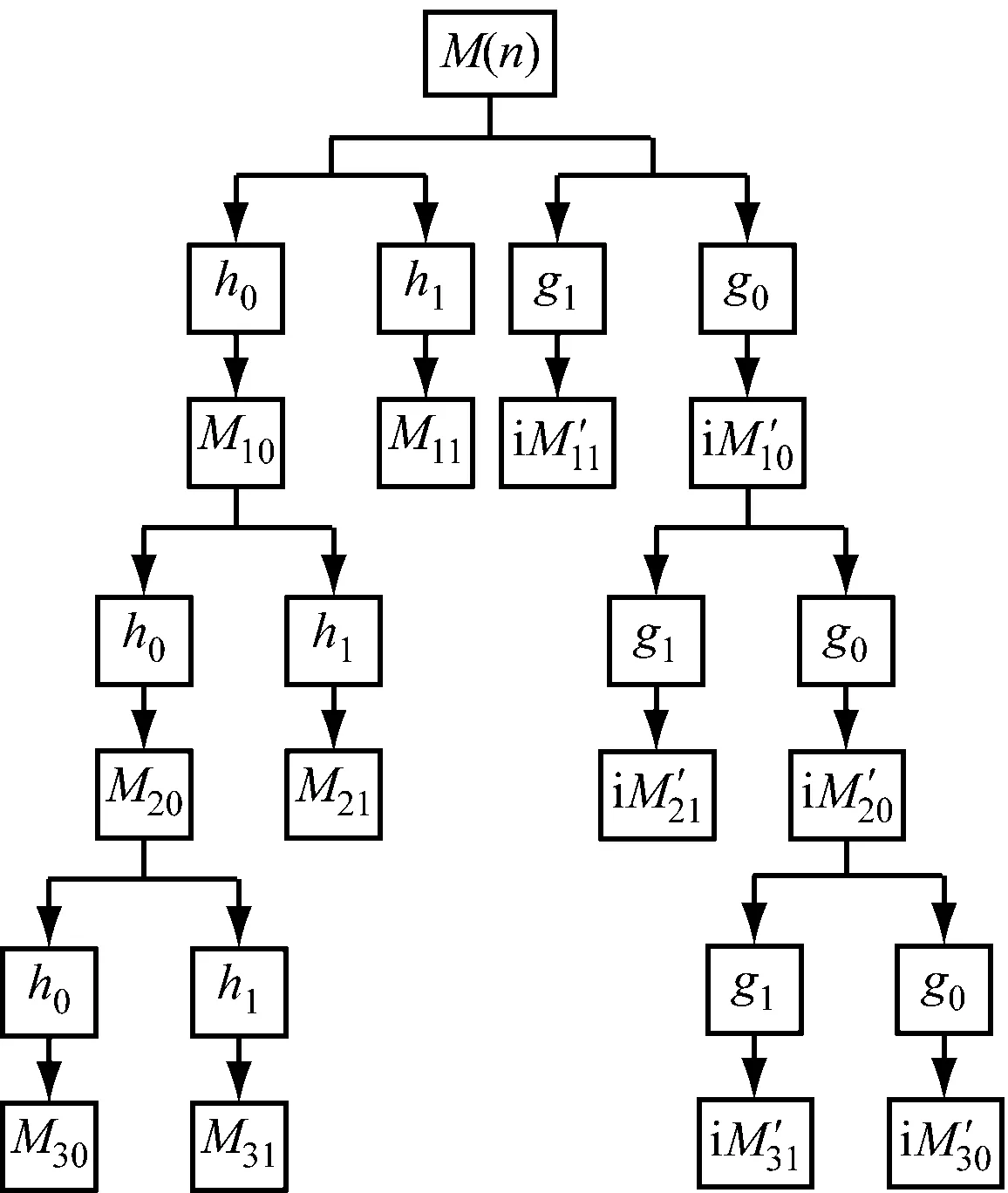
圖1 雙樹復小波變換3層分解過程Fig.1 Three-level decomposition process of dual-tree complex wavelet transform

經雙樹復小波變換分解后的高低頻信號可通過重構轉換為原始信號，如圖2所示。

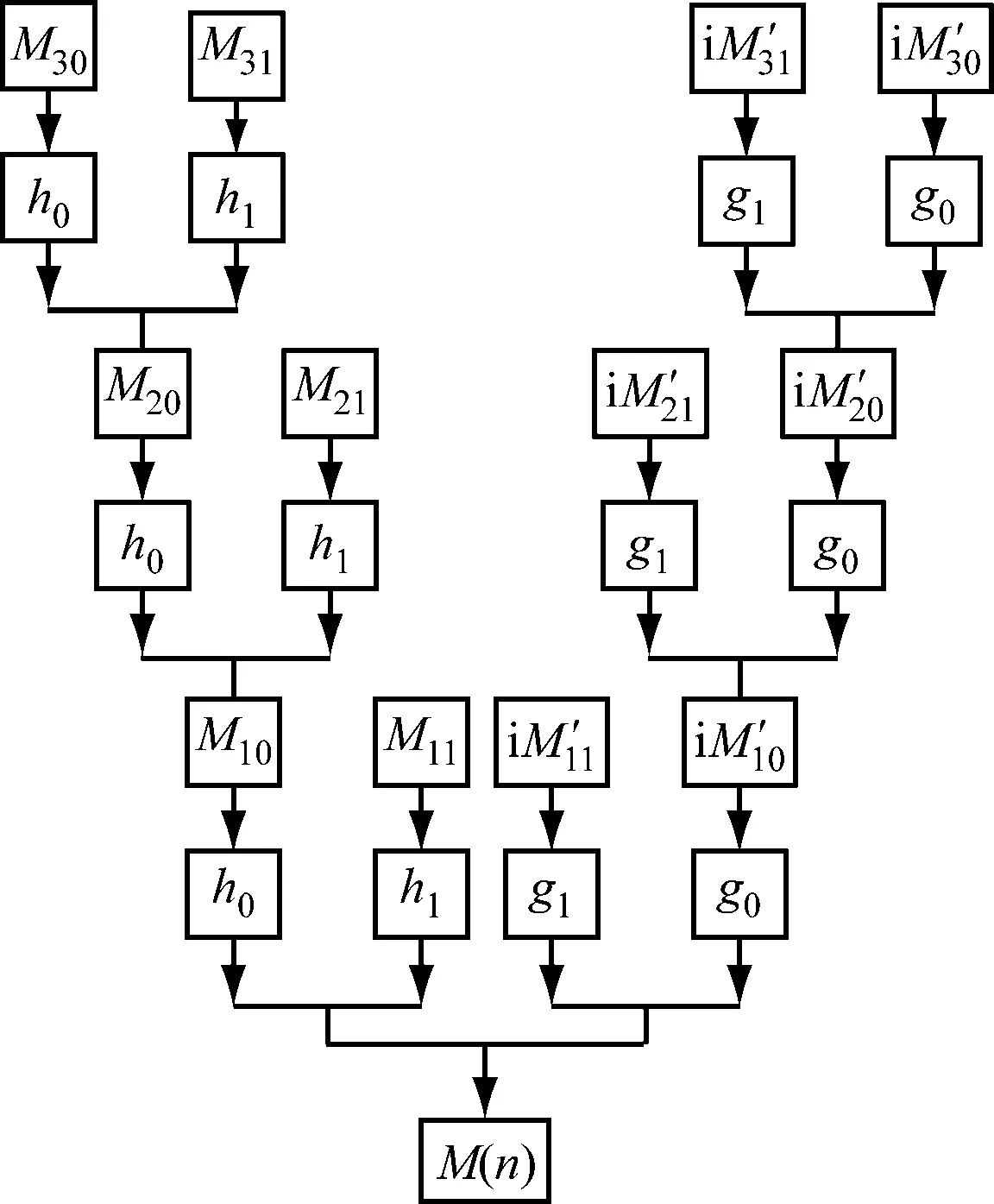
圖2 雙樹復小波變換3層重構過程Fig.2 Three-level reconstruction process of dual-tree complex wavelet transform

2 基于雙樹復小波變換的鋼絲繩損傷檢測信號處理方法

基于雙樹復小波變換的鋼絲繩損傷檢測信號處理流程如圖3所示。首先，確定所用小波基函數及小波分解層數，對檢測信號進行分解；然后，選擇合適的作用閾值方法并確定閾值，對分解信號進行去噪處理；最后，對信號進行重構，得到降噪后的信號。

圖3 基于雙樹復小波變換的鋼絲繩損傷檢測信號處理流程Fig.3 Signal processing flow of wire rope damage detection based on dual-tree complex wavelet transform

進行雙樹復小波分解時，若分解層數過少，則降噪效果較差，但過多的分解層數會導致計算量增大[9]。本文設計3層分解。采用Q平移法構造雙樹復小波變換高低通濾波器，得到高低頻信號分量。作用閾值在小波變換過程中具有重要意義[10]。與硬閾值相比，采用軟閾值降噪后，信號特征不會改變[11]，因此選用軟閾值對信號進行降噪處理，并采用最小極大方差軟閾值模型確定閾值。完成分量信號降噪處理后，對其進行重構，得到降噪后的原始信號。

3 鋼絲繩損傷檢測試驗

為了檢驗基于雙樹復小波變換的礦用鋼絲繩損傷檢測信號處理方法的有效性，在實驗室環境下進行鋼絲繩損傷檢測試驗。制備1根直徑為10 mm、長度為800 mm的鋼絲繩，在距離鋼絲繩一端200 mm處人為制造1處寬5 mm、深2 mm的局部損傷，如圖4所示。采用電動機、滾輪等搭建鋼絲繩損傷檢測試驗平臺[12]，如圖5所示。

圖4 鋼絲繩損傷Fig.4 Wire rope damage

圖5 鋼絲繩損傷檢測試驗平臺Fig.5 Experimental platform of wire rope damage detection

鋼絲繩損傷檢測信號由漏磁傳感器獲取，檢測過程如圖6所示。永久磁鐵對鋼絲繩勵磁至磁飽和，電動機驅動鋼絲繩運動。基于霍爾元件的漏磁傳感器檢測鋼絲繩徑向和軸向上的漏磁量和磁通變化，檢測信號依次經差分運算放大器、濾波電路、模數轉換電路處理后傳輸至計算機。在Matlab軟件環境下，采用雙樹復小波變換對檢測信號進行處理。

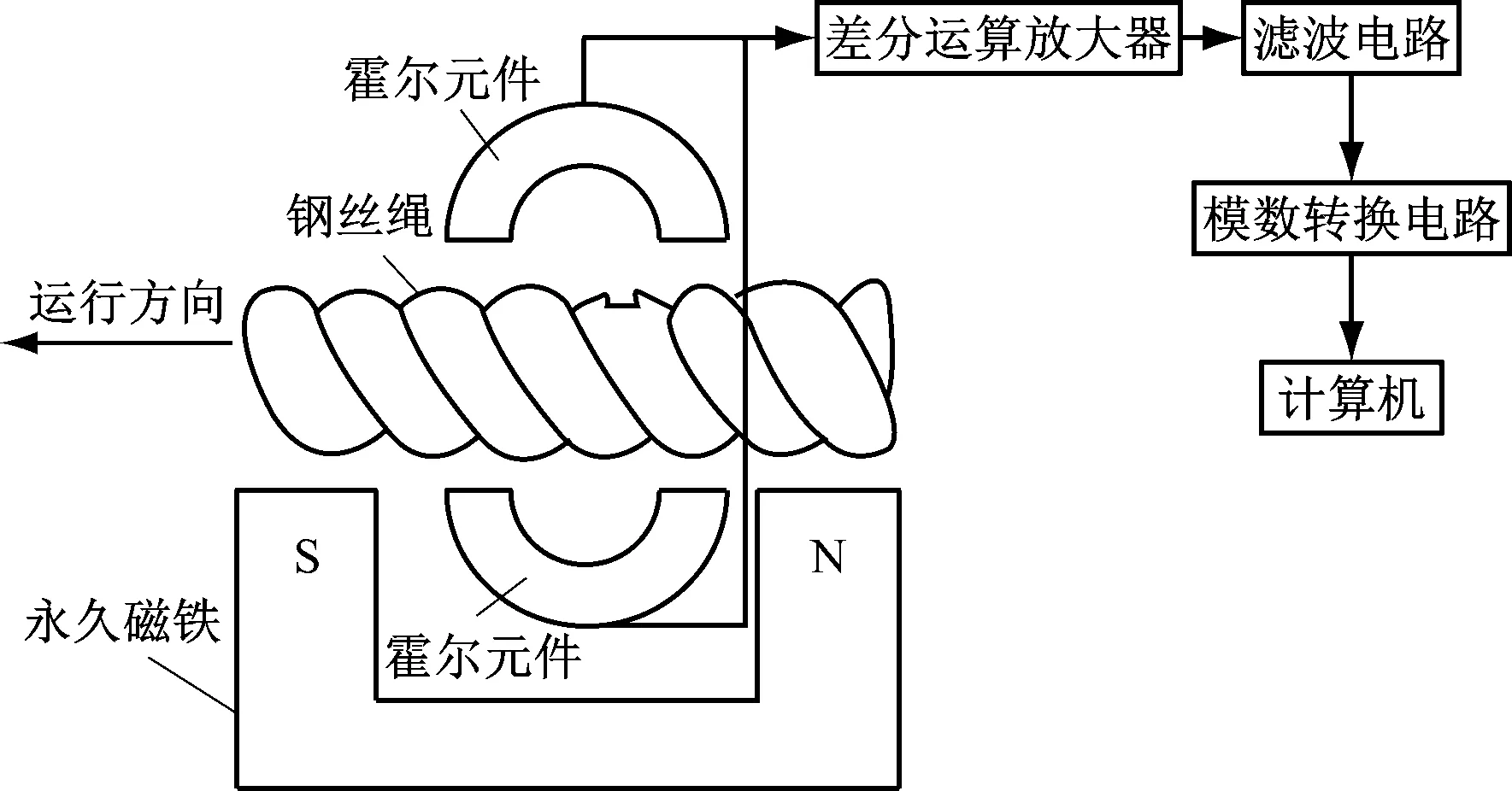
圖6 鋼絲繩損傷檢測過程Fig.6 Wire rope damage detection process

4 試驗結果分析

鋼絲繩損傷檢測原始信號如圖7所示，可看出信號中含有大量噪聲，難以分辨出損傷信號。完成檢測信號的雙樹復小波變換3層分解后，對各層分解系數進行單分量重構得到的信號如圖8所示，其中a3為近似信號(低頻信號)，d1，d2，d3為細節信號(高頻信號)。可看出鋼絲繩損傷檢測信號的奇異點(受損點)約在試驗開始后120～130 s處。

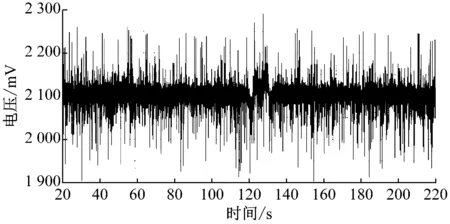
圖7 鋼絲繩損傷檢測原始信號Fig.7 Original signal of wire rope damage detection

圖8 經雙樹復小波變換3層分解后的單分量重構信號Fig.8 Reconstruction signals of each component after three-layer decomposition by dual-tree complex wavelet transform

分別采用雙樹復小波變換和經典小波變換對檢測信號進行處理，處理過程中均采用最小極大方差軟閾值模型確定作用閾值。試驗結果如圖9所示。

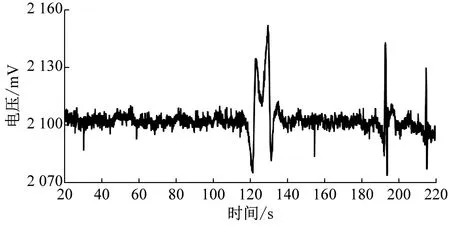
(a) 基于雙樹復小波變換

從圖9可看出，鋼絲繩損傷檢測信號經雙樹復小波變換處理后，尖峰和突變數量明顯減少，信號整體平穩，去噪效果明顯；奇異點處信號峰值明顯變大，有利于后續特征提取；盡管在2×105ms，2.2×105ms處存在尖峰，但該處信號不符合鋼絲繩損傷故障特征，不會導致誤判。而采用經典小波變換對鋼絲繩損傷檢測信號進行處理后，信號整體不平穩，奇異點處信號不明顯，且存在多處類似奇異點的尖峰和突變，易導致鋼絲繩損傷故障誤判。

計算經不同方法處理后信號的信噪比R，結果見表1。信噪比越大，則降噪效果越好。

(1)

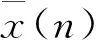
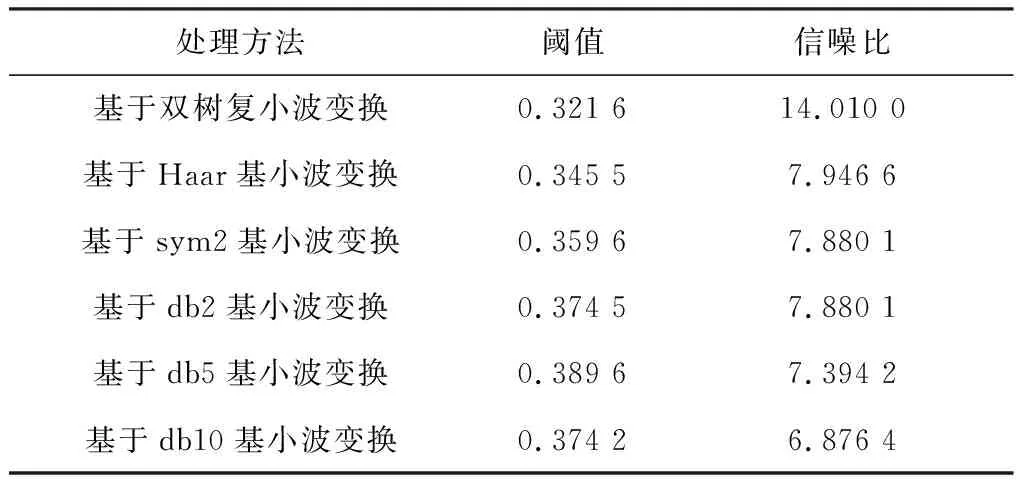
表1 經不同方法處理后的鋼絲繩損傷檢測信號信噪比Table 1 Signal to noise ratios of wire rope damage detection signal processed by different methods

根據圖9和表1可知，采用雙樹復小波變換對鋼絲繩損傷檢測信號的降噪效果優于經典小波變換，有利于提高鋼絲繩損傷檢測準確度。

5 結論

(1) 采用電磁檢測法檢測礦用鋼絲繩損傷情況時，受井下惡劣環境影響，檢測信號中包含大量噪聲，且存在尖峰和突變干擾，增大了損傷信號定性和定量識別難度。采用雙樹復小波變換對鋼絲繩損傷檢測信號進行處理可較好地去除噪聲，得到分布較明顯的鋼絲繩損傷特征信號，避免了小波變換存在的平移不變性較差、頻帶混疊等問題，有利于對鋼絲繩損傷情況作出準確判斷。

(2) 在實驗室環境下搭建了鋼絲繩損傷檢測試驗平臺，對基于雙樹復小波變換的鋼絲繩損傷檢測信號處理方法的降噪性能進行驗證，結果表明：該方法可有效減少檢測信號中的尖峰和突變數量，使信號平穩，降噪效果優于經典小波變換，且增大了奇異點處信號峰值，有利于后續特征提取。