基于空化的液膜密封熱流體動態特性分析?

孫鑫暉， 閆方琦， 郝木明， 力 寧， 翁澤文， 袁俊馬

（1.中國石油大學（華東）新能源學院 青島，266580） （2.中國航發湖南動力機械研究所 株洲， 412002）

引 言

作為機械密封［1-2］的一種類型，非接觸式液膜密封因具有密封效果優良、可靠性高、能耗低和抗干擾能力強等優點，得到廣泛應用。目前，在液膜密封方面對空化的研究較為豐富。文獻［3-4］通過實驗對空化現象進行了研究。文獻［5-7］通過理論計算，分析了Reynolds 和JFO（Jakobsson Floberg Olsson，簡稱JFO）2 種空化邊界條件。Ma 等［8］通過實驗與仿真對比，研究了空化產生的吸力對密封的影響。學者們對密封動態特性也進行了研究。Hao 等［9］分析了空化對密封動態特性參數的影響。楊文靜等［10］建立了考慮錐度和波度的液膜密封數學模型，分析了錐度和波度對密封動態特性的影響。在密封的熱效應方面，Luan 等［11］基于熱流體動壓潤滑模型，討論了各種參數對密封間隙流體熱行為的影響。Qiu等［12］建立了可用于預測密封摩擦副溫度和壓力的三維熱流體動壓模型。在螺旋槽液膜密封方面，分析其動態特性在熱黏和空化共同影響下的研究較少。

筆者以螺旋槽液膜密封為研究對象，建立了基于空化效應的液膜密封熱流體動力學特性模型。在計入空化效應的基礎上，利用有限元法求解了動態雷諾方程，得到了液膜動態特性系數，并分析了在熱黏和空化作用下，密封環的槽數、槽深以及液膜密封工作時的轉速和壓力對動態特性系數的影響，為完善液膜密封潤滑機理及密封結構設計提供了參考。

1 計算模型

1.1 幾何模型

圖1 為液膜密封端面結構示意圖。ro，rg，ri分別為密封環外徑、槽根半徑和密封環內徑；密封環周向槽 臺 寬 比γ=ag/(aw+ag)；ag，aw分 別 為 周 向 槽 寬和周向臺寬；pi為密封環內徑側壓力；pw為密封環外徑側壓力；α為螺旋角；θ為轉角；ω為密封環轉速，旋轉方向如圖1 所示；密封環端面上螺旋槽線型為對數螺旋線。

圖1 液膜密封端面結構示意圖Fig.1 Schematic diagram of liquid film sealing end face

1.2 數學模型

1.2.1 控制方程

為簡化計算過程，計算做以下假設［13］：①潤滑流體為牛頓流體，流動為層流；②由雙相混合物組成的薄膜分為全液膜區和空化區，空化區的壓力保持不變；③全液膜區域中的流體是不可壓縮的；④忽略由流體熱帶來的摩擦副熱變形。

基于上述假設，適用于液膜密封端面流體流動的柱坐標動態Reynolds 方程［14-16］為

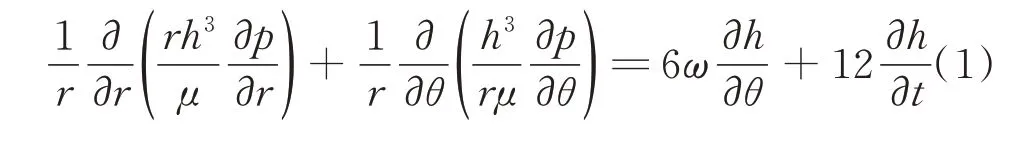
1.2.2 擾動方程

密封擾動模型如圖2 所示，其中靜環受到三方向擾動。假設密封受到了激勵頻率為f的相對穩態平衡位置的軸向及2 個正交角微小擾動，則動態膜厚方程可表示為

由此微小擾動造成的相對穩態平衡壓力的擾動壓力方程為

圖2 密封擾動模型Fig.2 Perturbation model of seal

1.2.3 能量方程

采用含有對流、擴散、耗散項的能量方程描述液膜溫度，其柱坐標表達式為

其中：ρ為流體密度；c為流體比熱容；ω為動環速度；k為流體熱傳導系數；μ為流體動力黏度。

黏度μ滿足黏溫關系式

其中：μ0為溫度在T0時的流體黏度；β為黏溫系數。

1.2.4 邊界條件

1）強制性邊界條件

密封環外徑

密封環內徑

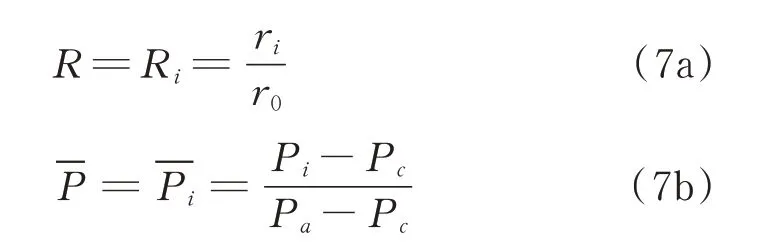
2）周期性邊界條件

3）JFO 空化邊界條件為

2 動態特性系數的求解

聯立式（1）～（3）對動態方程進行求解，考慮到軸向擾動Δzeift的數值很小，且在徑向方向的改變幾乎 為0，可 認 為(Δzeift)2=同時，穩態參數不隨時間發生變化，故將式（2），（3）代入式（4），得到如下方程。

穩態Reynolds 方程為

軸向動態微擾Reynolds 方程為

引入無量綱變量，得到無量綱液膜剛度和阻尼的表達式為

其中：Ω為求解區域；j=z，γX，γY。

3 計算結果及分析

3.1 模型正確性驗證

為了驗證本數值計算方法的正確性，搭建試驗臺如圖3所示。試驗用的碳化硅靜環內徑為46.25 mm，外徑為55.25 mm，螺旋角為27°，槽深為12 μm。為了保證可以觀察到端面的空化現象，使用透明石英制作動環。在密封運轉過程中，通過相機拍攝端面間的空化現象，計算空化區域與試驗空化區域如圖4 所示。可以看出，數值模擬的空化區域與試驗的空化區域基本一致，驗證了本程序模型的正確性。

圖3 密封試驗臺與密封裝置圖Fig.3 Test rig and test structure

3.2 結構參數對動態特性的影響

計算用到的結構參數如表1 所示。若無特別說明，均按表中數值進行計算，求解的動態系數均為無量綱量。

圖4 計算空化區域與試驗空化區域Fig.4 Cavitation area of simulation and test

在液膜密封中，動態系數保持如下規律：Kxx=Kyy，Dxx=Dyy，Kxy=?Kyx，Dxy=?Dyx。由于數值計算時以同一方向為基準，因此會出現負數情況，但其抵抗擾動的能力大小依然由其絕對數值表示。由文獻［17］及后續計算可知，耦合系數Kzx，Kxz，Kzy，Kyz、Dzx，Dxz，Dzy，Dyz以及角向阻尼Dxy，Dyx的數值量級很小，可忽略不計并視為0。

3.2.1 槽數

根據筆者所建立的模型，在保持其他參數恒定的情況下，求解槽數從12 增加到26 時的各個動態參數。圖5 為槽數對動態特性的影響。圖5（a）在考慮熱黏和空化的影響下，軸向剛度系數Kzz和角向剛度系數Kxx，Kyy均隨著槽數的增加而逐漸增大；角向耦合剛度系數Kxy，Kyx均隨著槽數的增大而少許減少。阻尼系數隨槽數的變化如圖5（b）所示。軸向阻尼系數Dzz與角向阻尼系數Dxx，Dyy的絕對值隨著槽數的增加而略有減小。槽數的增減對空化的發生并沒有明顯影響，但由于考慮了熱效應對液膜的影響，槽數的增加會使端面流體的冷卻效果增強，液膜的溫度降低，促使液體黏度升高，從而在一定程度上影響了液膜剛度和阻尼。可見，增加槽數有助于增強液膜抵抗外界干擾的能力。

圖5 槽數對動態特性的影響Fig.5 Influence of groove number on sealing dynamic characteristics

當考慮熱黏效應的影響時，其端面間液膜溫度的變化會引起液膜黏度的改變，即端面間液膜黏度不再均勻分布，各角向之間的相互影響較弱，耦合角向系數的變化比正角向及軸向系數的變化要小。

3.2.2 槽深

在保持其他參數恒定的情況下，動態特性參數隨槽深的變化如圖6 所示。圖6（a）中，軸向剛度系數Kzz和角向剛度系數Kyy，Kxx隨著槽深的增加而大幅增加，而耦合角向剛度系數Kxy，Kyx隨著槽深的增加，其絕對值會有降低，但整體變化較小。圖6（b）中，軸向阻尼系數Dzz和角向阻尼系數Dxx，Dyy隨著槽深的增加而緩慢減小。槽深對液膜動態特性的影響與槽數相類似，隨著槽深的增加，空化區域開始變小，而槽深的增加可以增大端面流量，有效降低端面溫度，從而使液膜的黏度升高，在兩者的共同影響下，液膜的抗干擾能力顯著增強。

圖6 動態特性參數隨槽深的變化Fig.6 Influence of groove depth on sealing dynamic characteristics

3.3 工況參數對動態特性的影響

3.3.1 轉速

圖7 為轉速對動態特性的影響。由圖7（a）可知，剛度系數的絕對值隨著轉速的增加而增大，轉速升高能夠明顯增加流體動壓效果。阻尼系數受轉速的影響如圖7（b）所示，阻尼系數隨著轉速的增大而迅速增大。隨著轉速的增加，動態特性參數的絕對值增加，且軸向系數高于角向系數，其中耦合角向系數最小，雖然轉速的增大會在一定程度上使空化區域增大，同時增加生熱量提高了液膜溫度并減小液膜黏度，但在本研究的轉速下，動壓效應對動態特性的影響程度大于熱黏與空化的影響。在5 kr/min 轉速下，轉速的升高可以增強流體動壓效應，明顯提高液膜的抗干擾能力。

圖7 轉速對動態特性的影響Fig.7 Influence of rotating speed on sealing dynamic characteristics

圖8 壓力對動態特性的影響Fig.8 Influence of pressure on sealing dynamic characteristics

3.3.2 壓力

在其他參數保持恒定的情況下，動態特性參數隨壓力的變化如圖8 所示。圖8（a）中，液膜剛度系數的絕對值隨著壓力的增大而增大，且軸向剛度系數Kzz的變化大于角向剛度系數的變化。圖8（b）中液膜阻尼系數同樣隨著壓力的升高而增大，軸向阻尼系數Dzz改變量高于角向阻尼系數。這是因為壓力的增大可以明顯增強流體的動壓效應，使液膜空化區域減少，同時摩擦生熱量上升，降低了液膜黏度，在這些因素的綜合影響下，液膜抗干擾能力有所增強。

4 結 論

1）在本研究工況下，由于轉速是影響液膜溫度和動壓效應的主要因素，因此該參數對液膜密封動態特性的影響程度要大于槽數、槽深以及壓力。

2）在考慮空化及熱黏條件下，各角向間動態特性系數的相互影響較弱，耦合角向系數小于正角向及軸向系數，且減少密封環螺旋槽的槽數、增加槽深、提高轉速或增加壓力均可使液膜抵抗外界干擾的能力增強。

3）在高轉速、高壓力等極端工況下的液膜密封動態特性研究有待進一步開展。