火箭發動機與尾翼座共用尾翼結構在高膛壓火炮膛內間隙影響因素

彭嘉誠， 蔣建偉， 廖偉， 盧易浩

(北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

0 引言

張開式尾翼是彈藥常采用的一類穩定裝置，在彈丸出炮口后，合攏的數個尾翼片釋放約束后從尾翼座打開，在外彈道起到保持穩定飛行的重要作用。為有效利用制導增程彈藥尾部空間、減小消極質量，國外研究人員發明了一種增程發動機與尾翼座共用的尾翼結構(以下簡稱共用尾翼結構)，著名的紅土地制導炮彈[1]就采用了該結構，如圖1所示。

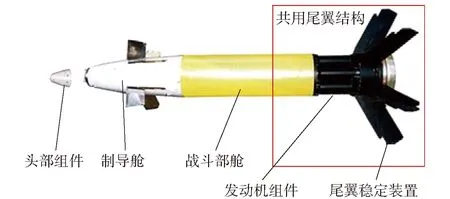
圖1 紅土地激光末制導炮彈[1]Fig.1 Red Land laser terminal guided projectile[1]

共用尾翼結構因其空間利用率高、有效載荷大等優點，在新型制導增程彈藥中也得到廣泛應用。然而采用大口徑線膛火炮作為發射平臺時，膛內高溫、高壓燃氣不僅使彈丸受到巨大軸向力，還將由于彈帶受膛線切割而受到較大的周向扭轉力。二者結合可能造成尾翼片在膛內與其相鄰部件(如發動機殼體、戰斗部底座等)的間隙余量不足，發生卡滯和磕碰，進而造成尾翼片結構損傷，出炮口后不能正常張開，導致掉彈等嚴重事故。因此，深入開展典型制導增程彈藥膛內各部件的結構變形研究是非常重要的。

現階段采用理論計算和試驗觀測均較難以準確描述彈丸在火炮膛內的每時刻運動狀態。文獻[2-5]采用數值模擬方法完成了不同彈炮間隙、卡膛速度、初始擺角及摩擦熱等因素對膛內彈丸擠進過程的影響規律研究，證明了數值模擬方法應用在彈丸膛內過程研究的有效性。針對身管結構變化，孫河洋等[6]、陸野等[7]建立具有不同坡膛結構的彈炮有限元模型，研究了坡膛結構變化對內彈道性能的影響。丁傳俊等[8]采用數值方法研究了磨損身管對內彈道性能的影響。許耀峰等[9]針對漸速、等齊、混合3類膛線結構下大口徑火炮發射減旋滑動彈帶制導彈藥擠進和膛內運動階段開展數值模擬，獲得了膛線結構對彈炮動力學響應的影響。針對彈- 炮耦合結構變化，劉雷等[10]、過斌等[11]建立彈丸與身管接觸碰撞模型，研究了彈炮接觸碰撞及匹配性問題。黃德隆等[12]針對某型制導炮彈滑動彈帶與膛線間隙，導入火藥氣體燃燒數據，建立了彈丸膛內流動模型來模擬不同間隙條件下的壓力分布。針對彈丸發射安全性，謝輝[13]采用有限元分件軟件Autodyn仿真計算了復雜發射環境下炸藥裝藥的動力學響應。徐赫陽等[14]采用有限元分析軟件LS-DYNA對某線膛火炮戰斗部發射強度進行仿真分析，得到戰斗部在膛內各階段的應力、應變曲線，并開展了驗證試驗。王韞澤等[15]采用Autodyn軟件，針對膛內存在異物時彈體和身管的動態響應進行數值模擬，研究成果得到了故障復現試驗驗證。廖偉等[16]對彈丸偏心質量形成的靜不平衡和力偶不平衡兩種狀態膛內過程進行仿真研究，結果表明橫向過載、章動角能反映彈丸在膛內的不穩定擺動，適用于表征彈丸在膛內的不穩定性。

綜上所述，關于彈丸在火炮膛內的運動規律及發射安全性分析已取得一些研究成果，但直接針對帶有共用尾翼結構的彈藥在火炮膛內受火藥氣體沖擊后全過程復雜響應的研究還較少。本文針對采用共用尾翼結構的典型制導增程類彈藥由大口徑線膛炮發射時的膛內過程開展數值模擬，獲得彈丸膛內每時刻的動力學響應；通過比對出炮口速度、轉速試驗數據來驗證數值模擬正確性；針對典型增程類彈藥的發動機殼體在不同屈服強度和緊固螺釘在不同預緊力加載狀態下膛內各部件的變形、軸向壓縮量及各尾翼片與戰斗部底座間隙變化規律開展研究。本文成果可為采用共用尾翼結構的增程類彈藥膛內結構強度故障預防及分析提供參考。

1 模型與算法

1.1 物理模型

針對采用共用尾翼結構的增程類彈藥建立簡化物理模型(見圖2)，其中制導艙與戰斗部艙按質量等效原則進行簡化，忽略內部細節，采用相同形狀的鋼圓錐、圓柱體模擬，調整其內部體積，保持與原結構質量、質心等結構參數一致，其余部件與真實結構尺寸一致。共用尾翼結構主要包括戰斗部底座、發動機殼體、尾翼片(對稱分布4片)、發動機支座、滑動彈帶、閉鎖機構等，其中發動機殼體(4套管)上部套入留有4預制孔的戰斗部底座，發動機下部依靠4組緊固螺釘固定于托座，托座再與發動機支座固連。滑動彈帶與文獻[9]中結構一致(見圖3)，采用彈帶、滑動環及彈體配合結構，在線膛炮發射時減少膛內彈體轉速，以保護制導炮彈電子器件。

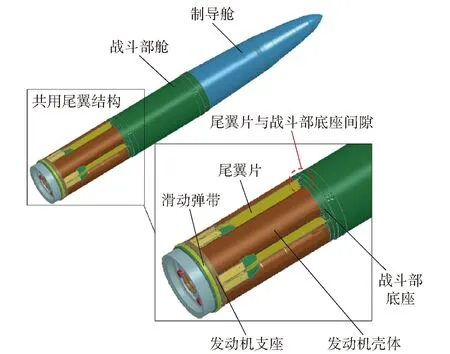
圖2 典型增程類彈藥簡化物理模型Fig.2 Typical simplified physical model of extended-range ammunition

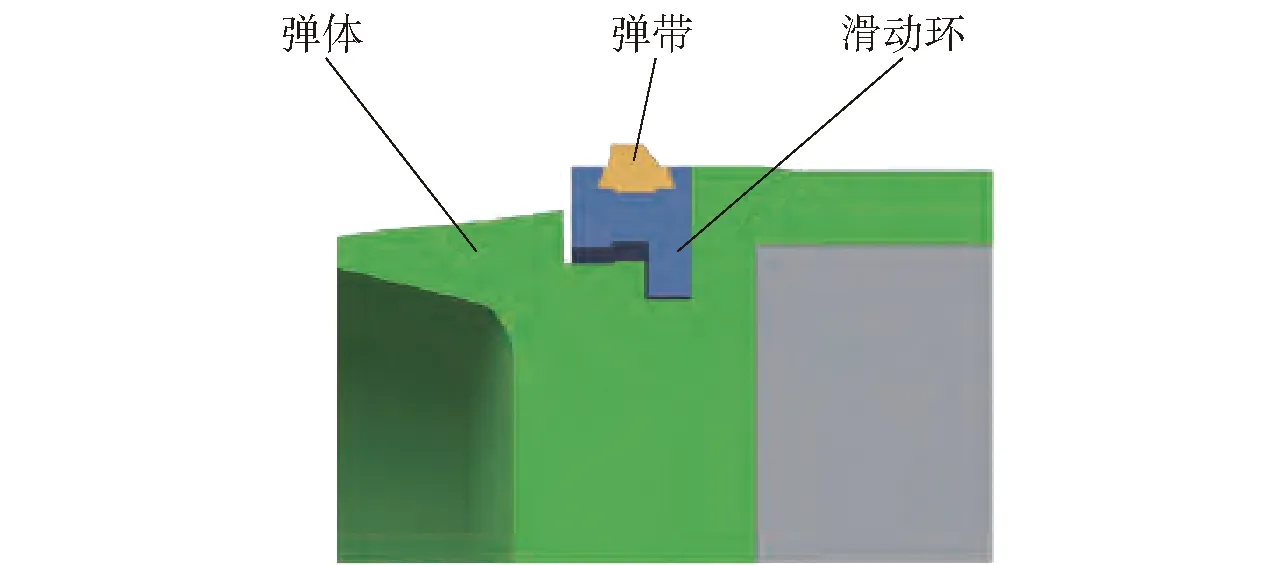
圖3 滑動彈帶結構[9]Fig.3 Structure of slipping driving band[9]

設共用尾翼結構中發動機殼體、戰斗部底座及發動機殼體支座在膛內受載后發生的軸向壓縮量分別為Δδc、Δδb、Δδs.圖2中各尾翼片與底座的初始間隙均為a0=2.8 mm，圖4中對稱分布的4片尾翼(按順時針方向分別為1號、2號、3號、4號)膛內受載后與戰斗部底座的實際間隙分別為a1、a2、a3、a4，相對初始間隙a0的各尾翼片與底座相對間隙分別為a1/a0、a2/a0、a3/a0、a4/a0.

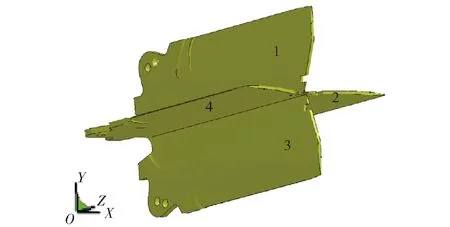
圖4 4片尾翼片Fig.4 Four tail fins

同樣地，發動機殼體、戰斗部底座及發動機殼體支座相對軸向壓縮量分別為Δδc/a0、Δδb/a0、Δδs/a0，則總軸向相對壓縮量表示為

Δδ/a0=(Δδc+Δδb+Δδs)/a0.

(1)

1.2 離散化模型

火炮發射的增程類彈藥結構較為復雜，制導艙、戰斗部艙未直接受火藥氣體作用，按簡化物理模型剖分網格；彈帶在膛內受膛線切割將出現大變形和破壞，利用TrueGrid軟件建立彈帶部件的六面體網格模型；采用Hypermesh軟件按真實結構建立其余部件的四面體網格模型。彈丸離散化模型如圖5所示。

圖5 彈丸離散化模型Fig.5 Projectile discretization model

基于圖6(a)所示真實身管膛線結構[12]，依據真實坡膛、陰線與陽線結構建立具有膛線的身管離散化模型，如圖6(b)所示。

圖6 火炮身管Fig.6 Artillery barrel

1.3 材料模型

通常材料模型及模型參數是影響數值模擬結果準確性的最重要因素。數值模擬中所有部件材料均采用各向同性與隨動硬化混合模型PLASTIC_KINEMATIC描述，根據Cowper-Symonds模型，動態屈服應力σy為

(2)

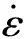
采用應變失效準則，當單元應變達到預設失效應變fs時，單元失效并被程序自動刪除，通常取

εr=ln (1+ε0)，

(3)

(4)

式中：εr為材料斷裂時真實應變；ε0為參考應變；ζ為模型失效真實應變放大系數。所用材料的參數如表1所示，其中在正常彈丸膛內運動中，一般只有彈帶部件發生大變形和破壞失效，故只設置了彈帶材料的失效應變。

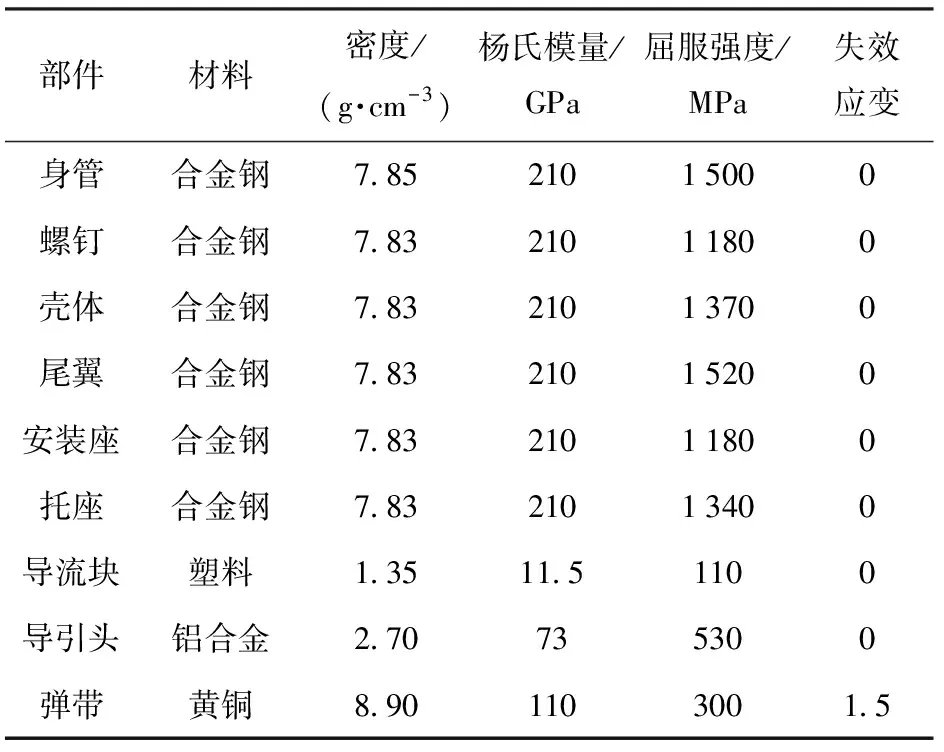
表1 材料參數Tab.1 Material parameters

1.4 算法選擇

數值模擬采用厘米- 克- 微秒單位制，采用LS-DYNA軟件提供的Lagrange計算方法，使用*BOUNDARY_SPC_SET關鍵詞固定身管底端面。不考慮火藥燃燒過程，用*LOAD_SEGMENT_SET關鍵詞將彈底膛壓pd(t)曲線(最大膛壓為196 MPa，時刻t=9.3 ms)加載至彈丸底部，模擬膛內過程火藥燃氣對彈丸的作用，設置彈丸與身管為自動面- 面接觸。圖7所示為彈丸膛內運動計算模型，其中彈丸底部黑色區域為膛壓曲線加載區域。

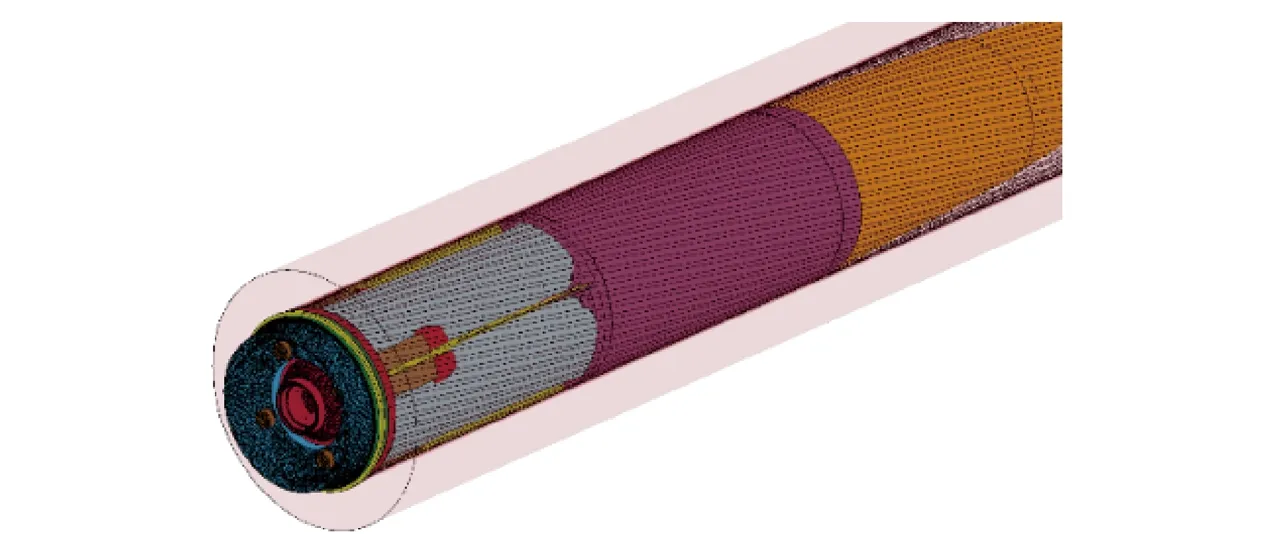
圖7 彈丸膛內運動計算模型Fig.7 Calculation model of projectile motion in bore

2 影響因素及工況設計

影響膛內尾翼片與戰斗部底座間隙的因素較多，下面針對共用尾翼結構中易引起此間隙變化的主要部件進行分析。

發動機殼體在彈丸膛內運動過程中為發動機主要承力部件，在彈尾共用尾翼結構中體積占比大，膛內受載時發動機殼體發生彈性或塑性變形后引起的軸向壓縮量較大，可能出現發動機本身并未發生塑性變形和破壞，但由于彈性變形引起的總壓縮量已超過尾翼與戰斗部底座間隙，從而使得尾翼片與底座發生磕碰。而殼體材料屈服強度與變形大小密切相關，文獻[17]表明在典型殼體材料熱處理工藝過程中，由于回火溫度不同，合金鋼屈服強度將發生較大變化(768～1 421 MPa)。殼體材料采用的Cowper-Symonds模型中靜屈服強度σs為獨立變量，可通過設置不同σs值來表征由于加工等因素產生的屈服強度波動。正常工藝條件下發動機殼體靜屈服強度為1 370 MPa，為研究發動機殼體屈服強度對各部件軸向壓縮量以及尾翼- 底座間隙的影響，分別設置殼體靜屈服強度為1 370 MPa、1 100 MPa和800 MPa.

在共用尾翼結構中，發動機殼體依靠4組螺釘固定于發動機支座上，支座與彈帶組件直接相連。在彈帶受膛線切割旋轉時將依次帶動發動機支座、螺釘及發動機殼體等部件。4組緊固螺釘預緊力加載狀態對發動機殼體膛內扭轉變形影響較大，進而影響尾翼與戰斗部底座間隙。依據緊固螺釘的安裝要求、外徑和螺紋圈數計算得到螺釘預緊力后，轉化為壓力邊界條件，大小為150 MPa，使用*LOAD_SEGMENT_SET關鍵詞施加在緊固螺釘上表面。然而預緊力真實狀態較難獲知，本文按預緊力缺失的極限條件處理，設置3種典型預緊力加載狀態A、B、C，分別對應圖8所示均勻施加預緊力狀態、缺失1組預緊力狀態、缺失2組預緊力狀態。

圖8 不同預緊力加載狀態(紅色虛線框中的螺釘無預緊力加載，其余為正常預緊力加載)Fig.8 Different preloading states (the screws in the red dotted boxes are not preloaded, and other screws are normally preloaded)

依據不同發動機殼體屈服強度與緊固螺釘預緊力狀態設計計算工況，如表2所示。

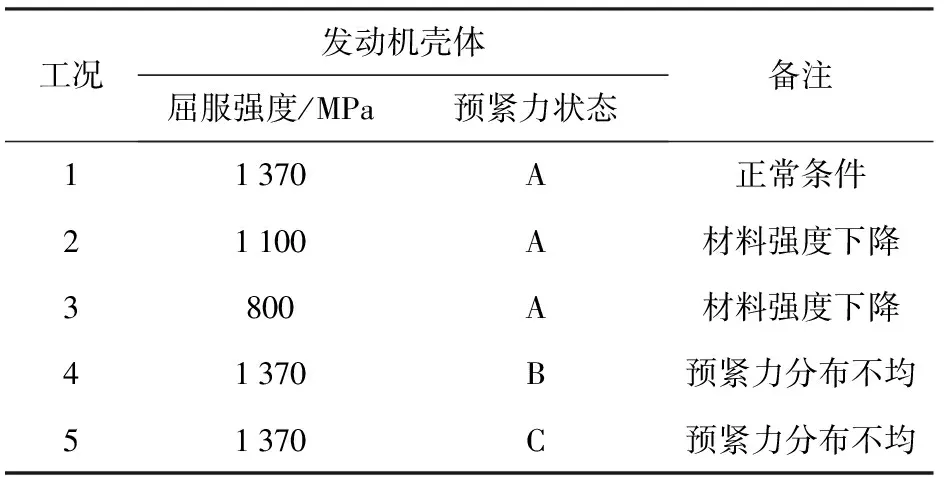
表2 工況設計Tab.2 Operating condition design

3 膛內運動狀態

3.1 彈丸膛內運動狀態

圖9所示為數值模擬得到的典型時刻膛內運動彈丸位置。圖10給出了彈丸滑動彈帶在沖擊擠進階段的應變云圖，其中t取值0～2.4 ms為彈帶擠進膛線階段，t=16.2 ms時刻彈丸出炮口。

圖9 典型時刻彈丸膛內運動位置Fig.9 Position of projectile at typical moment

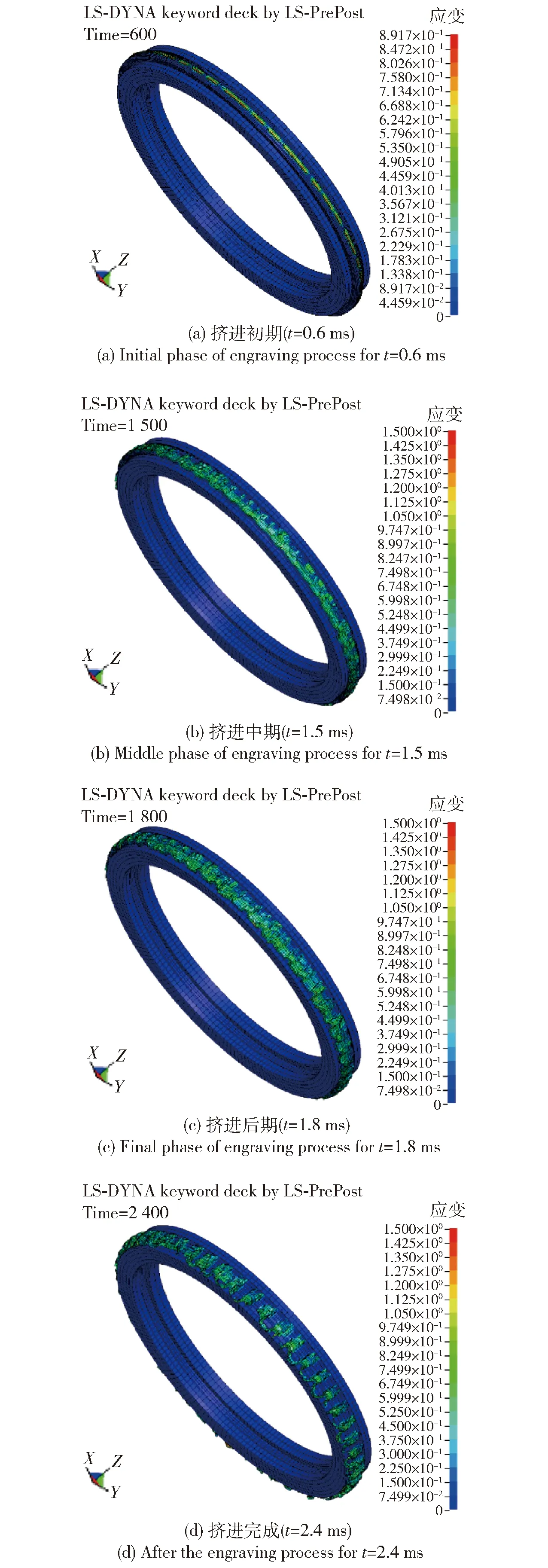
圖10 滑動彈帶沖擊擠進階段應變云圖Fig.10 Strain of slipping driving band during engraving

彈丸在膛內的速度、轉速及加速度是表征彈丸內彈道性能的重要運動參數。彈丸各部件除彈帶外在膛內同步運動且并未發生太大塑性變形，故在LS-Prepost軟件中取彈丸圓柱部整體，可觀測到彈丸速度- 時間曲線和加速度- 時間曲線。取彈丸圓柱部最大直徑處多個節點作為觀測點，以觀測點每時刻的平均轉速作為彈丸轉速，隨時間的變化曲線如圖11所示。

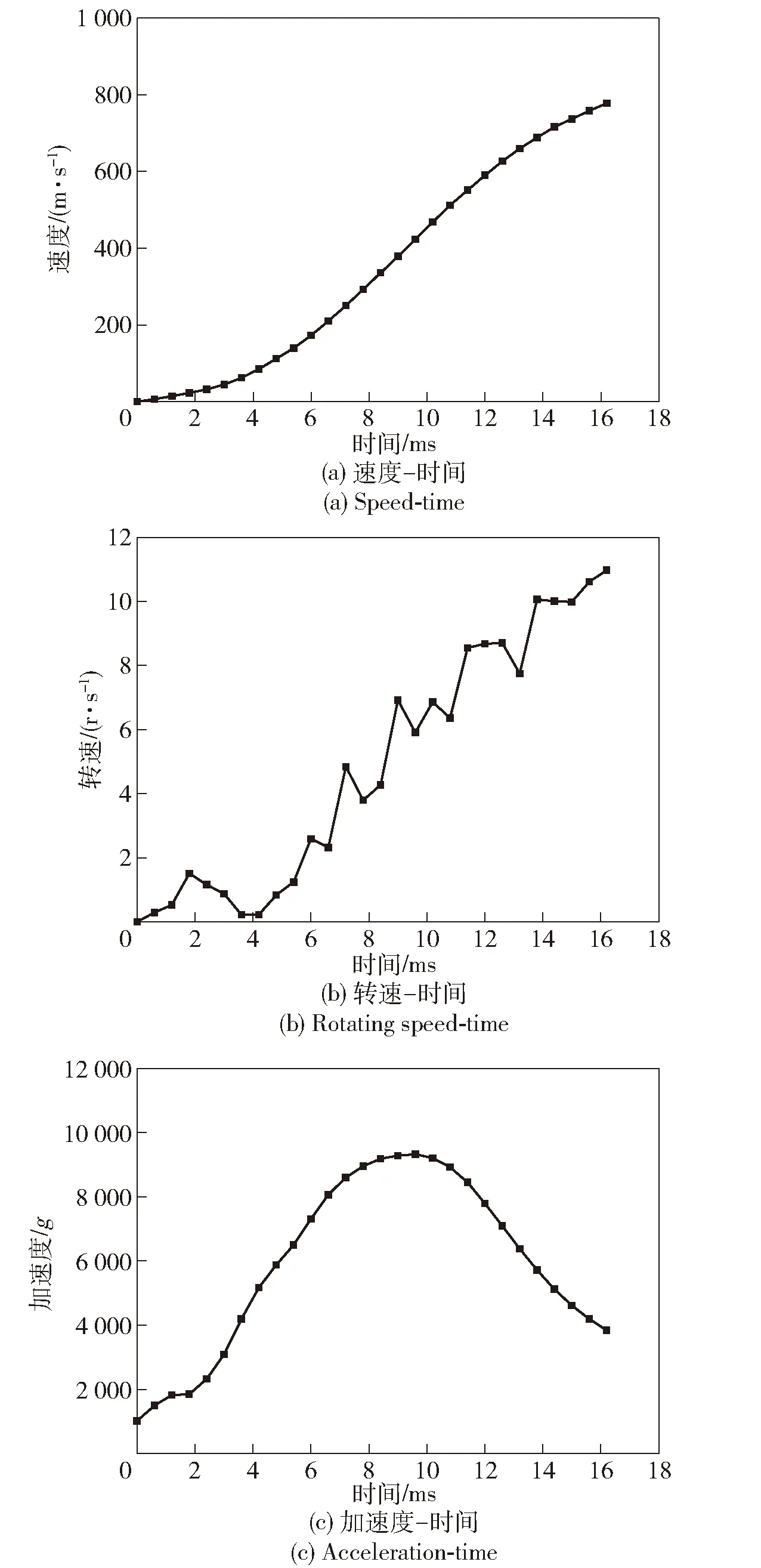
圖11 彈丸膛內運動時程曲線Fig.11 Time history curve of projectile movement

由圖11可知：彈丸在膛內加速度隨時間先增加后減小，與膛壓變化趨勢一致；彈丸速度增長趨勢先大后小，彈丸轉速總增長幅度小，且往往先增長后又回落，并重復這一過程，曲線較不光滑。這是因為該彈丸采用了滑動彈帶，其復雜減速機理導致了此現象，同時極大地減小了該彈的出炮口轉速。

3.2 炮口速度、轉速驗證

表3給出了炮擊試驗實測與數值模擬得到的彈出炮口速度與轉速值。

表3 出炮口速度與轉速Tab.3 Muzzle velocity and rotating speed

由圖9、圖10、圖11可知，彈丸膛內運動數值模擬可清晰地展現彈帶與膛線相互作用并使彈丸按預期導向旋轉的過程，可獲得彈丸在膛內每時刻運動參數。由表3中的數據可知，彈丸出炮口速度、轉速和試驗值吻合較好，表明本文所建立的數值模擬計算模型和方法可信。

4 各部件軸向壓縮量

圖12、圖13、圖14分別給出了工況1(發動機殼體屈服強度為1 370 MPa，螺釘預緊力為狀態A)發動機殼體及支座、戰斗部(底座)在最大膛壓時刻(t=9.3 ms)的應變與軸向位移云圖。

圖12 發動機殼體在最大膛壓時刻(t=9.3 ms)應變及軸向位移云圖Fig.12 Strain and axial displacement nephograms of engine shell at maximum pressure (t=9.3 ms)

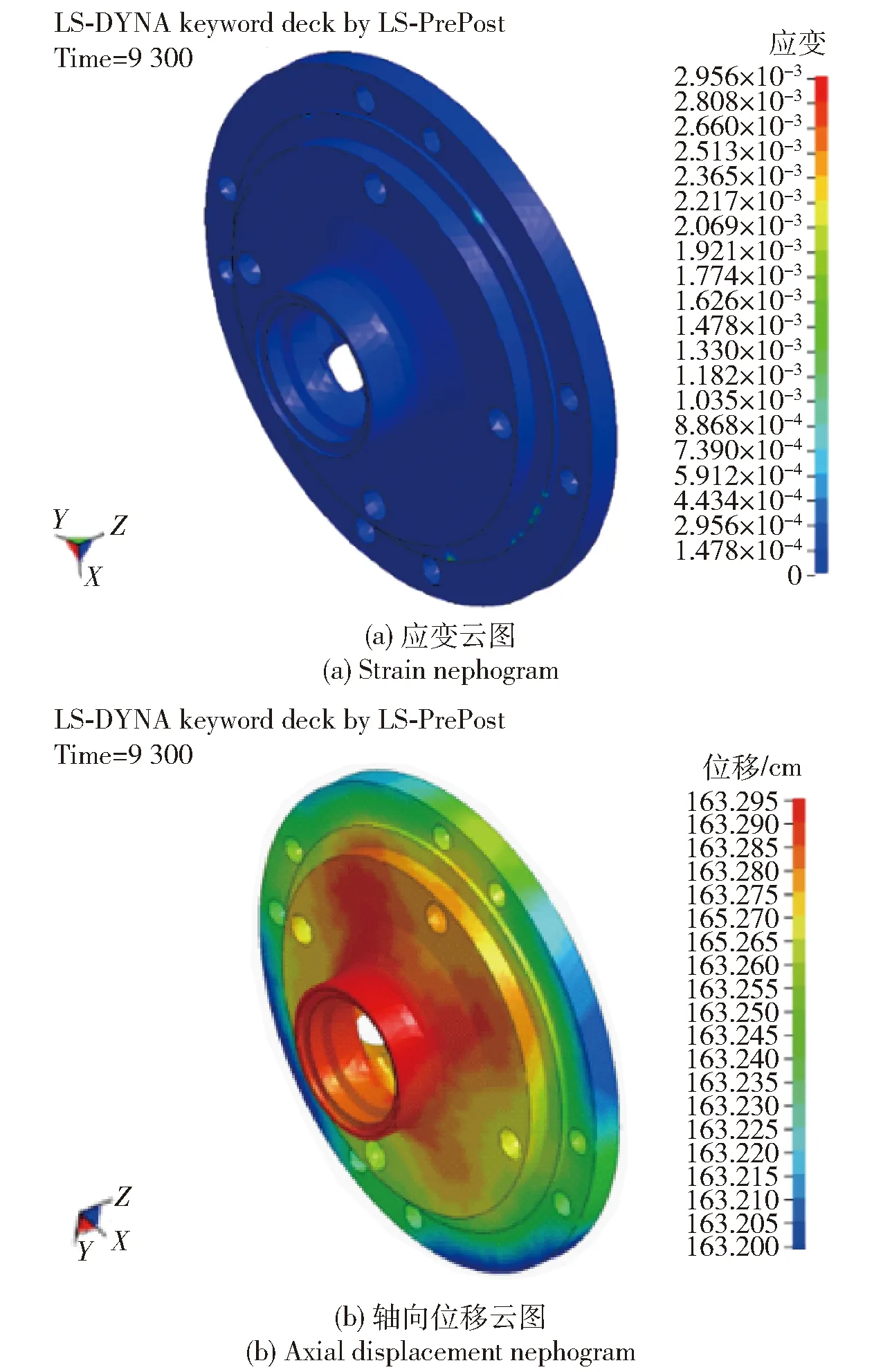
圖13 發動機支座在最大膛壓時刻(t=9.3 ms)應變及軸向位移云圖Fig.13 Strain and axial displacement nephograms of engine support at maximum pressure (t=9.3 ms)

由圖12、圖13、圖14圖可知，工況1條件下共用尾翼結構的主要部件(發動機殼體、支座與戰斗部)應變較小，但由彈性變形引起的軸向位移差，即軸向壓縮量較大，在殼體強度降低、預緊力缺失的條件下，軸向壓縮量將會更大。圖15所示為發動機殼體、戰斗部底座、發動機殼體支座及總軸向相對壓縮量(Δδc/a0、Δδb/a0、Δδs/a0、Δδ/a0)隨時間變化關系曲線。圖16所示為各部件總相對壓縮量隨時間變化關系曲線。

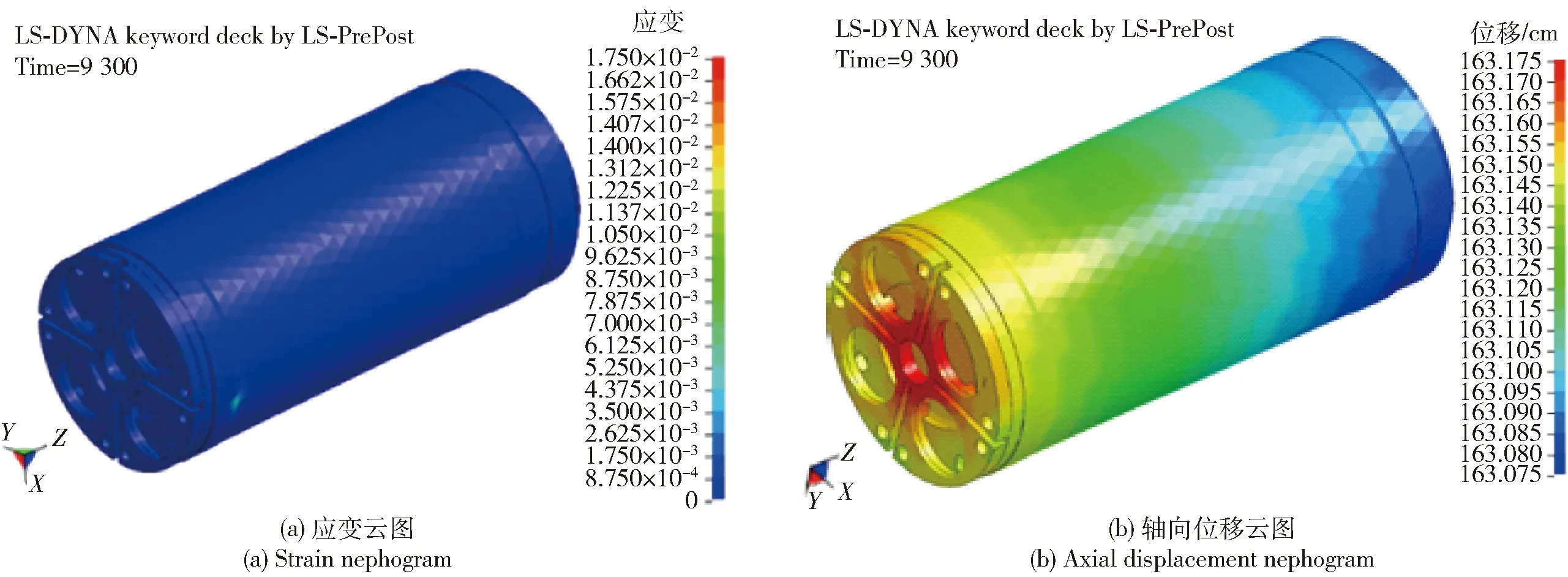
圖14 戰斗部(底座)在最大膛壓時刻(t=9.3 ms)應變及軸向位移云圖Fig.14 Strain and axial displacement nephograms of warhead (base) at maximum pressure (t=9.3 ms)

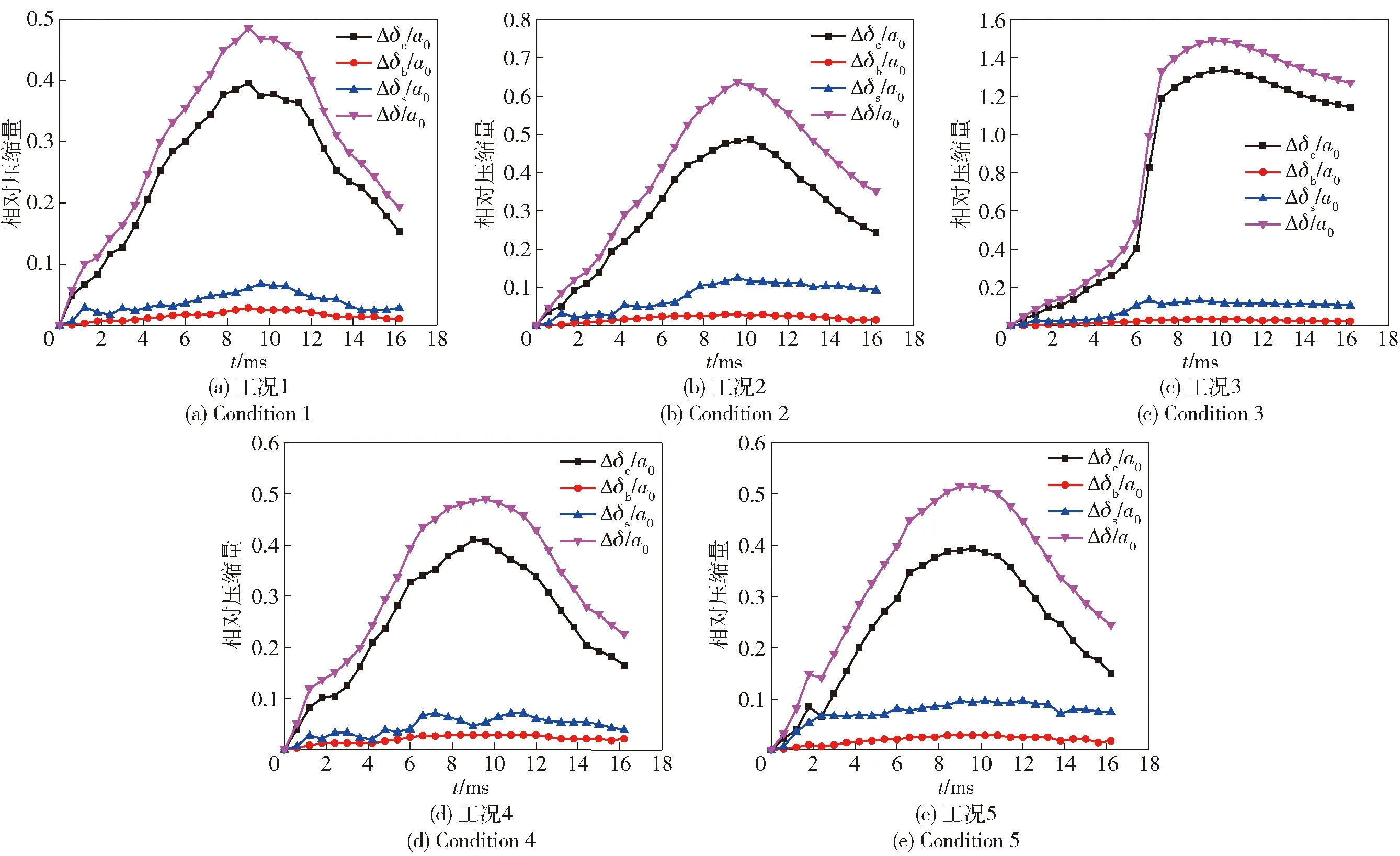
圖15 軸向相對壓縮量隨時間變化曲線Fig.15 Axial relative compression vs. time

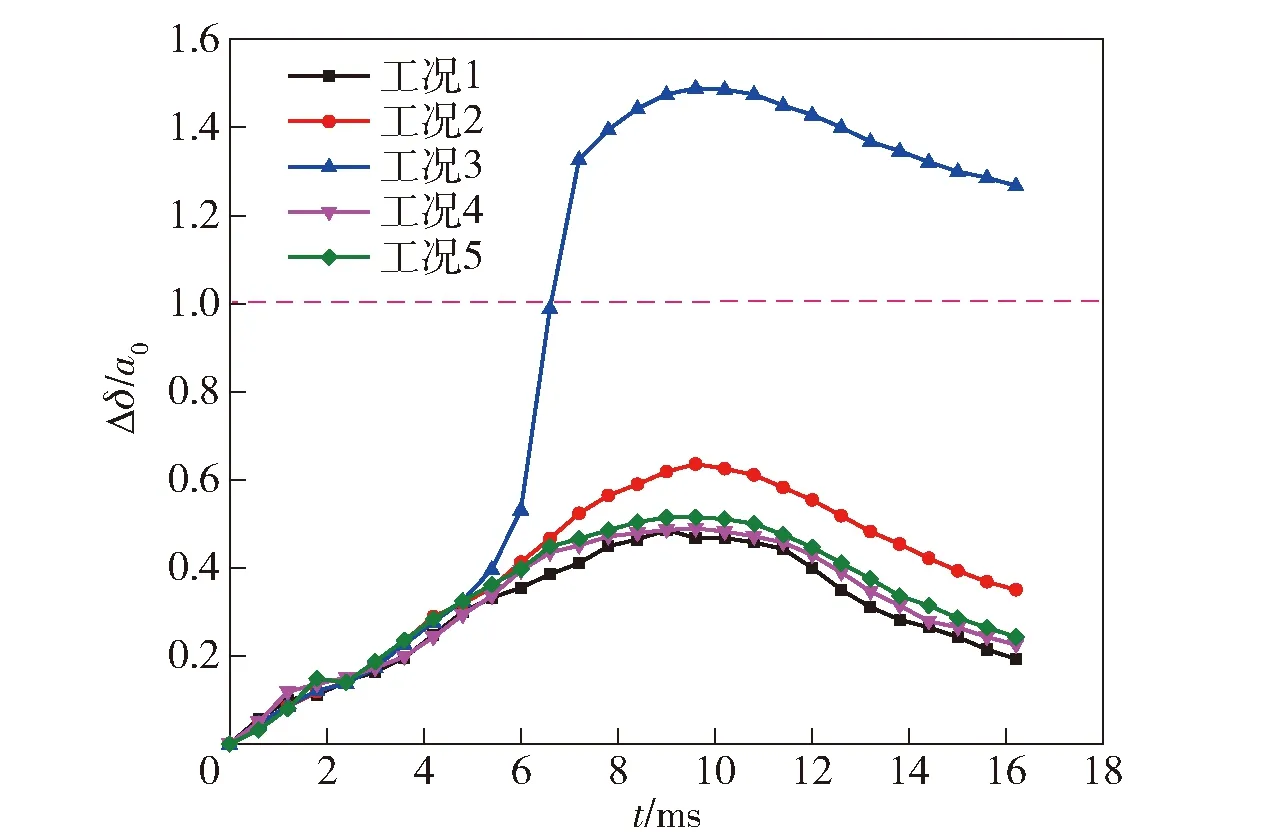
圖16 總相對壓縮量隨時間變化關系曲線Fig.16 Total relative compression vs. time

由圖15、圖16可知：發動機殼體、戰斗部底座、殼體支座及總軸向相對壓縮量隨時間變化先增后減，在最大膛壓時刻(t=9.3 ms)達到最大值，與膛壓- 時間曲線趨勢一致；各計算工況中發動機殼體的軸向壓縮量在總壓縮量中占比最大，平均占比達78.2%.

由圖15(a)可知，正常條件下(工況1)膛內每時刻總壓縮量均最小。由圖15(b)～圖15(e)可知，隨著發動機殼體靜屈服強度降低，各部件相對壓縮量急劇增大。圖15(c)表明，當降低到800 MPa(工況3)時，雖然在膛內壓力作用下，共用尾翼結構各部件本身并未發生塑性變形和破壞，但由于彈性變形引起的總壓縮量已超過尾翼與戰斗部底座間隙，即Δδ/a0>1，使得尾翼片與底座發生磕碰，底座將出現明顯凹痕。圖17所示為該條件下最大膛壓時刻(t=9.3 ms)尾翼片與戰斗部底座的應力云圖，圖18所示為該彈某次射擊試驗后拾取到的戰斗部底座照片，圖18中標識了在膛內戰斗部底座受4片尾翼撞擊后產生的不均勻凹痕。

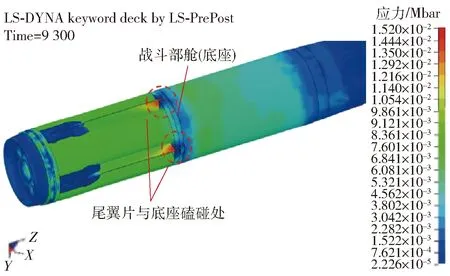
圖17 尾翼片與戰斗部底座磕碰應力云圖(t=9.3 ms)Fig.17 Stress nephogram of the collision between tail fin and warhead base (t=9.3 ms)

圖18 受尾翼片磕碰后戰斗部(底座)照片Fig.18 Photograph of warhead (base) hit by tail fins

表4列出了發動機殼體、戰斗部底座及殼體支座在最大膛壓時刻(t=9.3 ms)的軸向相對壓縮量，即時間軸的最大值。

由表4數據可知：最大膛壓時刻(t=9.3 ms)發動機殼體軸向壓縮量Δδc對尾翼- 戰斗部底座間隙影響最大，不小于尾翼- 底座初始間隙a0的39%；隨著發動機殼體靜屈服強度減小，其軸向壓縮量不斷增大，且在尾翼- 底座間隙的占比也不斷增大。

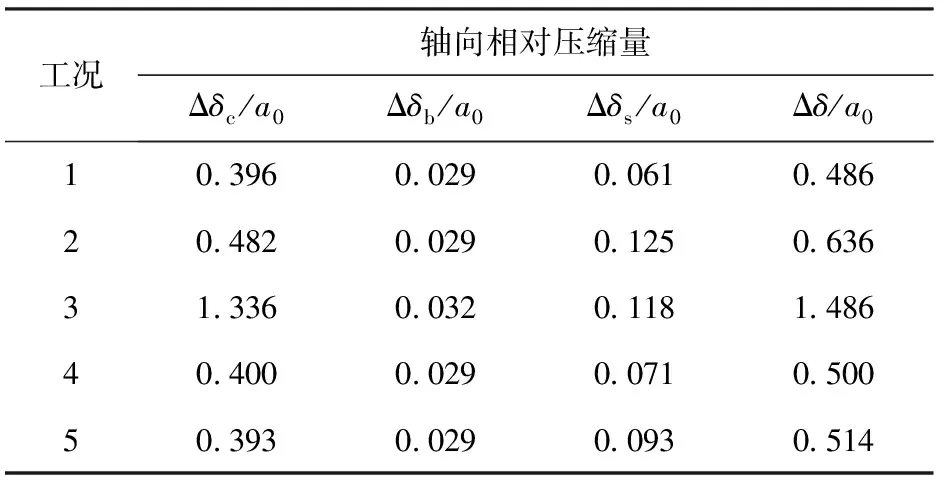
表4 軸向相對壓縮量Tab.4 Axial relative compression

圖19所示為最大膛壓時刻(t=9.3 ms)發動機殼體、戰斗部底座、殼體支座及總軸向相對壓縮量隨實際靜屈服強度與正常屈服強度比值的關系曲線。

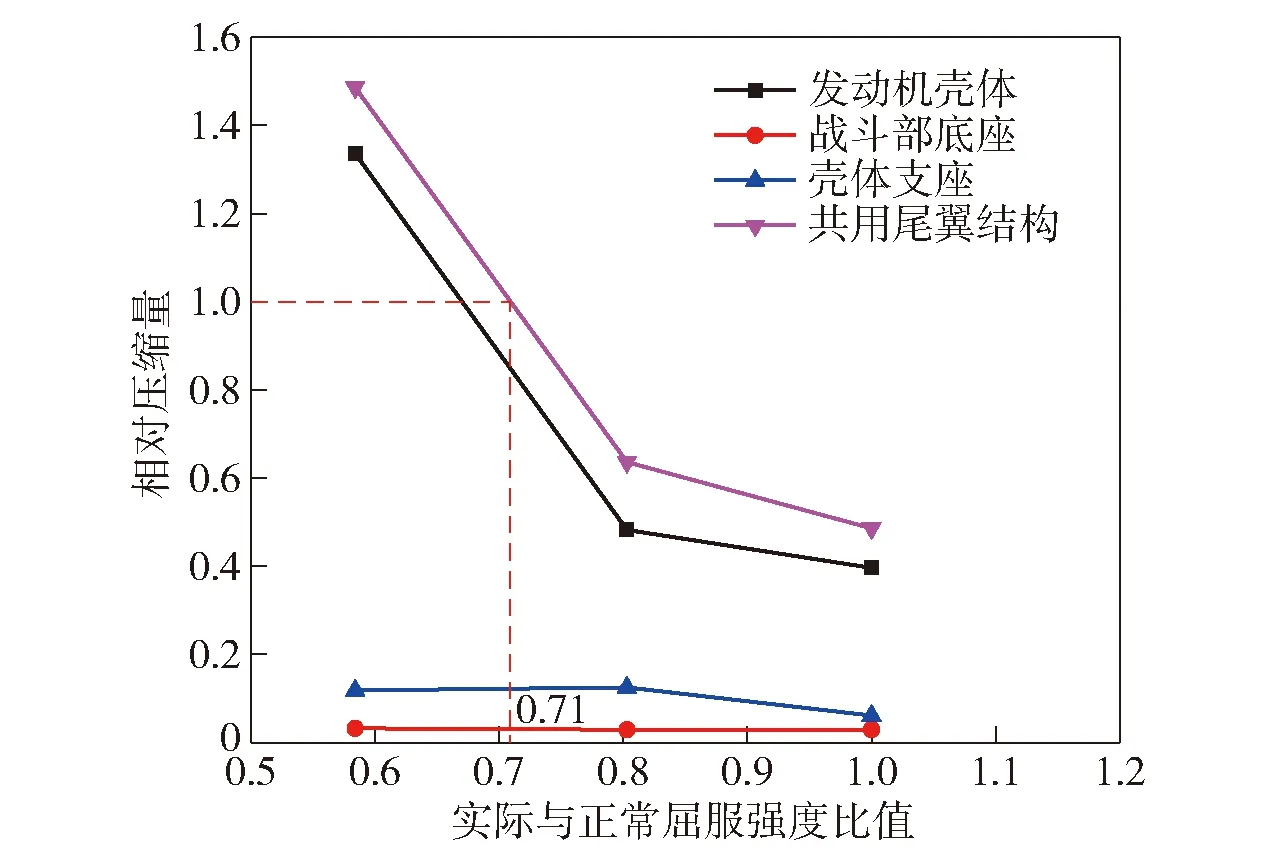
圖19 軸向壓縮量與實際與正常屈服強度比值關系曲線Fig.19 Relationship between axial compression and actual and normal yield strength

通過數值模擬結果可明確殼體處于不同靜屈服強度條件下尾翼與底座是否發生磕碰故障，假設共用尾翼結構中各部件在不同條件下壓縮量與屈服強度的關系是分段線性的，在圖19中用直線連接相鄰兩點，當共用尾翼結構的相對壓縮量為1.0時，尾翼與戰斗部底座發生磕碰，此時發動機殼體靜屈服強度臨界值為正常屈服強度的71%，即973 MPa.

5 各尾翼片與戰斗部底座間隙

圖20給出了預緊力狀態分別為A、B、C時，各尾翼片與戰斗部底座相對間隙(a1/a0、a2/a0、a3/a0、a4/a0)隨時間變化曲線。

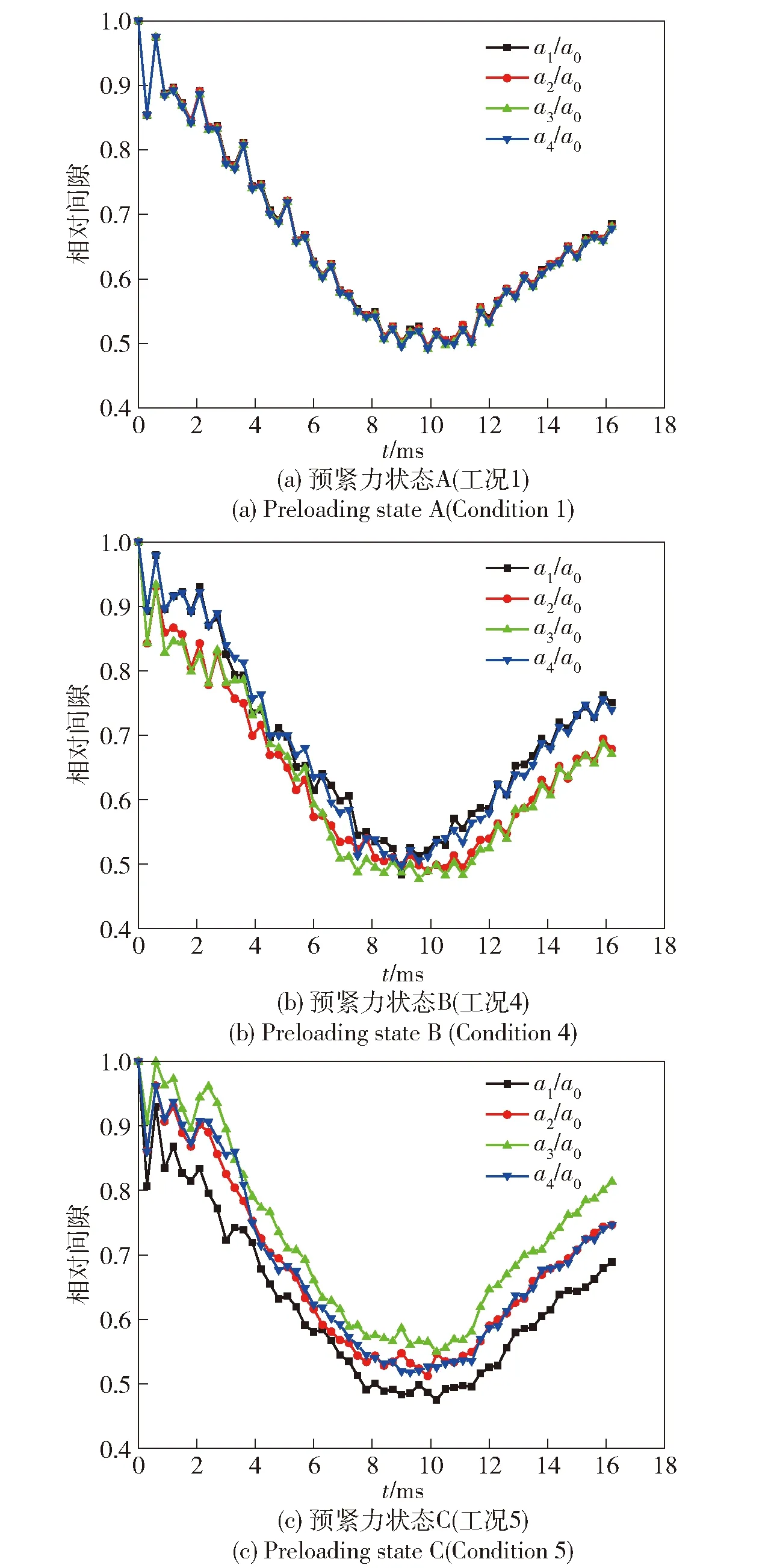
圖20 尾翼片與戰斗部底座相對間隙隨時間變化曲線Fig.20 The curve of the relative gap between each tail fin and the base of the warhead over time

由圖20可知，隨著螺釘預緊力狀態變差，各尾翼片與戰斗部底座的間隙在膛內每時刻出現明顯差別。分別定義1～4號尾翼片與戰斗部底座相對間隙在膛內某時刻t的最大值為max(ai/a0)、最小值為min(aj/a0)，即第i號尾翼片間隙最大，第j號尾翼片間隙最小。定義其差值為k(t)，

k(t)=max(ai/a0)-min(aj/a0).

(5)

圖21給出了數值模擬得到工況1、工況4、工況5的k(t)曲線。

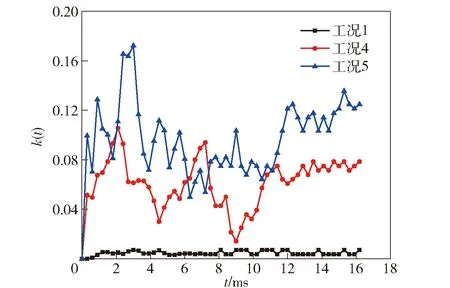
圖21 k(t)曲線Fig.21 Curves of k(t)

表5列出了k(t)在時間軸上的算術平均值ka與最大值kmax.

由圖21及表5數據可知：螺釘預緊力處于正常狀態A時，各尾翼片與戰斗部底座間隙在膛內每時刻基本一致；螺釘預緊力處于異常狀態B、C時，各尾翼片與戰斗部底座間隙在膛內不再同步，在預緊力缺失2組時，尾翼片與戰斗部底座間隙相差最大可達到初始間隙的17.3%；當膛內尾翼片與戰斗部底座發生磕碰時，不同尾翼片與戰斗部底座間隙大小不一就會造成尾翼片與底座磕碰程度不同，出現圖18所示的不同深淺磕碰痕跡。

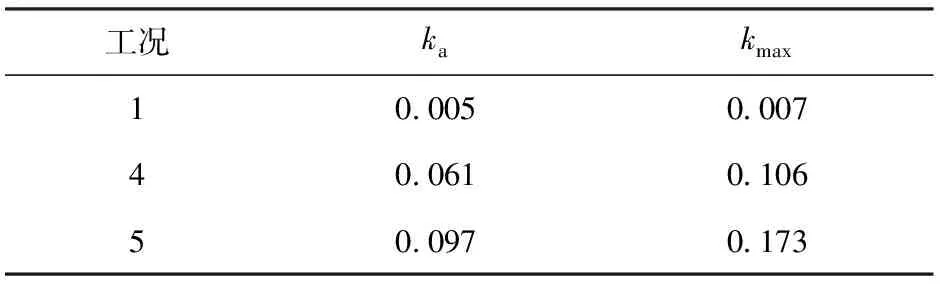
表5 k(t)均值與最大值Tab.5 Average and maximum values of k(t)

6 結論

本文采用數值模擬方法，對采用共用尾翼結構的典型增程類彈藥膛內過程進行了研究，分析了不同發動機殼體屈服強度與預緊力加載條件下彈丸膛內每時刻的動力學響應、共用尾翼結構主要部件的變形與軸向壓縮量及各尾翼片與戰斗部底座的間隙。得到主要結論如下：

1)共用尾翼結構各部件軸向壓縮量隨時間先增大后減小，與膛壓曲線趨勢一致，在最大膛壓時刻(t=9.3 ms)達到最大，且發動機殼體軸向壓縮量在總壓縮量中占比最大，平均占比達78.2%.

2)當發動機殼體屈服強度降低到800 MPa(工況3)時，在膛內壓力作用下，共用尾翼結構各部件本身并未發生塑性變形和破壞，但由彈性變形引起的總壓縮量已超過尾翼與戰斗部底座間隙，使得尾翼片與底座發生磕碰。

3)螺釘預緊力處于異常狀態B、C時，各尾翼片與戰斗部底座間隙在膛內不再同步，預緊力缺失2組時，間隙相差最大可達初始間隙的17.3%，在膛內尾翼片與戰斗部底座磕碰時，造成各尾翼片在戰斗部底座上產生深淺不一的磕碰痕跡。