V形柔性浮式防波堤消波特性研究*

冉小林 王 彬 段文杰 陳 凱 甘 進*

(武漢理工大學交通學院1) 武漢 430063) (武漢長江航道救助打撈局2) 武漢 430014)(武漢速安達建筑橡塑制品有限公司3) 武漢 430300)

0 引 言

浮式防波堤與其他傳統防波堤相比，可適應水深較大、地基軟弱、大潮差等水域，在港口海岸工程、海洋工程以及海水養殖等諸多領域具有廣闊應用前景.其中柔性浮式防波堤由充水和充氣囊體組成，其自身結構重量輕、儲備運輸空間小，并且展開撤收速度快，在臨時浮式防波堤方面具有較好的應用價值.

現階段對浮式防波堤的研究主要集中在防波堤的消波特性及防波堤新型結構上.Ataur等[1]利用水槽實驗研究了不同錨纜系統、不同水深、不同波浪周期等條件下浮式防波堤的水動力性能.Abdullah等[2]通過遺傳算法(GA)對雙浮式防波堤水動力性能進行了優化結構設計.Nikpour等[3]采用二維波浪水槽試驗對梯形浮式防波堤在深水規則波的衰減性能進行了綜合試驗研究.Christensen等[4]研究了帶翼板和兩側附有的多孔材質對浮式防波堤反射和透射的影響.丁寧等[5]基于線性勢流理論采用數值方法研究了V形浮式防波堤幾何參數對其消波效果的影響.針對柔性浮式防波堤，現階段的主要研究方法是通過模型試驗的方法，何成圓等[6]針對一種由單囊體組合而成的柔性浮式防波堤，分析了此防波堤的消浪機理.楊浩[7]針對一種層鋪式柔性浮式防波堤，通過物理模型的水池規則波試驗，研究分析了此防波堤的相對寬度、波陡、上部浮板、波浪繞射等因素對防波堤的透射系數、反射系數、繞射特性以及防波堤的運動響應和錨鏈系泊力的影響.汪宏等[8]針對一種圓木阻尼式柔性浮式防波堤，通過二維水槽中的規則波物理模型試驗，研究分析了該柔性浮式防波堤在有無浮板時的消浪性能.仇正中等[9]針對圓柱形柔性浮式防波堤的消浪特性，進行物理模型試驗，研究分析其在規則波和不規則波作用下的消浪特性，通過大量水槽試驗給出了圓柱形柔性浮式防波堤透射系數、反射系數、衰減系數與錨固方式、試驗水深、相對寬度的變化關系.

文中采用模型試驗和數值仿真相結合的方法對一種截面為圓形的V形柔性浮式防波堤的消波特性進行研究.在ANSYS-AQWA的線性三維輻射衍射模塊[10-11]中建立了柔性浮式防波堤的數值計算模型，在頻域內研究了防波堤的消浪性能，討論并分析了此數值方法的計算結果與試驗結果之間的關系，提出采用此數值計算方法來評估柔性浮式防波堤消浪性能的可行性.

1 分析模型及分析方法

1.1 分析模型

實驗模型見圖1，消波裝置主要由下部主水囊和上部為水囊提供浮力的兩個氣囊組成，單個浮體總長4 m，下部水囊直徑 0.4 m，上部氣囊直徑為0.1 m.試驗中采用了兩種布置方式：①V形布置，即兩水囊一端相連，形成V形結構，V形首部正對著波浪入射方向，V形的夾角分別為30°，45°和60°;②單水囊迎浪橫向布置.

數值計算模型采用前期開展的實驗模型.由于試驗過程中水池寬度為10.8 m，防波堤在水池寬度方向上的最大尺寸為4 m，相較于水池寬度，模型尺寸較小，且水池壁面上安裝了消浪裝置，以此避免波浪傳遞到水池壁面后反射波對試驗模型的影響，因此在數值模擬過程中，忽略水池壁面對防波堤計算模型的影響，數值計算模型見圖2.

圖1 試驗模型

圖2 數值計算模型

考慮錨泊系統對防波堤消波效果的影響，根據實驗中錨泊纜繩的布置方式，數值計算模型纜繩布置情況見圖3.試驗過程中水池水深為2 m，因此數值模型計算水深設為2 m，迎浪方向為X軸正向.由于防波堤下部主囊體為水囊，實際消波過程中，下部水囊完全浸沒于水中，依靠上部提供浮力的氣囊保證消波裝置的正常漂浮，因此試驗和數值計算中結構的吃水為0.4 m，同時，實際消波過程中上部的氣囊也參與了消波，圖4為柔性浮式防波堤截面示意圖.

圖3 防波堤錨泊纜繩布置情況

圖4 柔性浮式防波堤截面示意圖

1.2 數值分析方法

ANSYS WORKBENCH AQWA將AQWA的各個主要模塊集成在Hydrodynamic Diffraction和Hydrodynamic Response模塊中，功能完備，界面非常友好，易于操作.其Hydrodynamic Diffraction模塊主要進行浮體的輻射衍射分析，可計算得到浮體的相關水動力系數、浮體的靜態和動態響應問題，以及波浪傳遞給浮體的表面壓力等.Hydrodynamic Response模塊可以進行浮體的平衡分析，在輻射衍射分析基礎上給浮體結構添加錨泊系統，可計算得到錨泊狀態下浮體的靜水平衡位置、錨泊纜繩的張力，以及進行浮體的靜穩性分析.

由于在Hydrodynamic Diffraction中系泊纜繩無法參與計算，如需考慮錨泊系統對防波堤消波效果的影響，可以在輻射衍射分析模塊的Connection菜單中添加連接剛度考慮系泊系統的影響.本文柔性浮式防波堤首先在Hydrodynamic Diffraction模塊進行輻射衍射分析，然后在Hydrodynamic Response模塊進行平衡分析并且提取錨泊剛度后添加到Hydrodynamic Diffraction模塊再進行輻射衍射分析，最后采用AQWAGS進行后處理，輸出沿波浪入射方向波浪幅值的變化曲線，通過提取波前和波后的波浪幅值，就可得到防波堤的消波效率.

AQWA進行輻射衍射分析是純線性分析，計算的是規則波浪下的自由液面高度，最終輸出的結果是波幅值隨入射波方向的位置關系曲線.由公式H=Asin 2πft可知波面只是某一相位的函數，而波高幅值A是穩定不變的，輸出的幅值可代表此坐標位置的波高值.由波浪幅值隨入射波方向的位置關系曲線可得到堤前入射波高Hi和堤后平穩的波浪幅值Ht，進行相比得到波浪的透射系數Kt=Ht/Hi,繼而得到了防波堤的消波效率η=(1-Kt)×100%，即可表示柔性浮式防波堤的消波效果.

2 結果分析

試驗中，通過在防波堤堤前和堤后布置的多個浪高儀，可測量出試驗過程中防波堤堤前入射波高Hi和堤后平穩的波浪幅值Ht，通過計算便可得到防波堤的消波效率，圖5為試驗過程中進行堤前和堤后波高幅值的測量.

圖5 試驗中波高幅值的測量

利用AQWA分別建立夾角為30°，45°，60°的V形布置方式和單一囊體迎浪橫向布置的計算模型，將數值計算結果與試驗結果相比較，驗證此仿真方法的可行性和準確性.在計算消波效率時，使用AQWAGS打開模型的輻射衍射分析計算結果，得到波高幅值云圖，見圖6.提取波浪幅值沿波浪方向(即X軸負向)的變化曲線，可得到堤后的波高幅值，便可計算得到防波堤的消波效率，見圖7.由圖7可知，60°夾角布置方式下V形柔性浮式防波堤在波高0.075 m和波浪周期1.342 s的規則波作用下，波幅隨X軸的位置變化曲線，曲線的橫坐標為沿波浪入射方向X軸的各點坐標值，縱坐標為各點對應的波幅值，為入射波、衍射和輻射波的總和.圖7中的波高幅值變化曲線是有波動的曲線，是因為在仿真分析中由于入射和反射等不同波的疊加導致每個位置的波幅都有輕微的變化，導致曲線有些波動，以至于堤前的曲線類似于正弦的曲線，但是能明顯的觀察到堤后的波幅值要明顯的小于堤前的波幅值，并隨X軸坐標值的減小趨于穩定.根據結果顯示，堤前的大多位置的波幅值都大于實際計算設置的入射波的波幅值0.075 m，這是由于入射波與堤前反射波疊加導致的.

圖6 波高幅值云圖

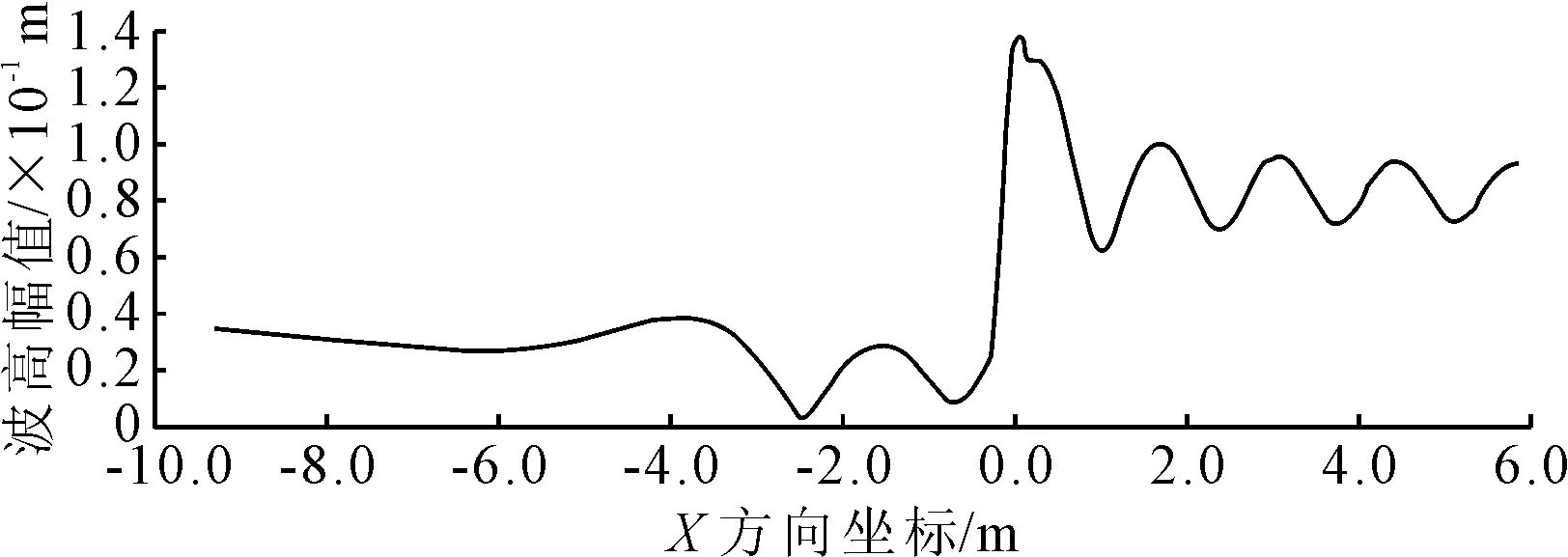
圖7 波浪幅值沿波浪方向變化曲線

為了研究柔性浮式防波堤的消波機理以及為柔性浮式防波堤設計提供技術參考，將主要探究不同波浪周期對柔性浮式防波堤消波效果的影響，不同波高對柔性浮式防波堤消波效果的影響，以及不同布置方式對柔性浮式防波堤消波效果的影響.同時，將數值計算結果與試驗結果進行對比分析，驗證此數值仿真方法的可行性和準確性.

2.1 波浪周期對防波堤消波效果的影響

試驗和數值分別計算了波高0.075 m、波浪周期T=1.118，1.342，1.565，1.789 s下柔性浮式防波堤的消波效率，見圖8.

圖8 波浪周期對消波效率的影響

數值和試驗結果表明，不同布置方式下防波堤消波效率都隨波浪周期的增加呈現先增加后減小的趨勢，在周期T=1.342 s時的消波效果最好.從整體數值計算結果上看，數值模擬計算得出的消波效率較物理試驗結果普遍偏小，其誤差值在6%～15%，這是由于物理試驗存在能量損耗，包括自然消耗和試驗水池等試驗設施對波浪能的消耗，然而在數值仿真中只有防波堤能吸收波浪能量，外界不吸收波能，以及試驗中波浪產生的摩擦破碎所消耗的部分能量在數值仿真中無法考慮.再加上試驗中防波堤采用的是充壓水囊，是柔性結構，波浪作用于防波堤時會導致囊體有明顯的變形，會吸收掉部分的波浪能，而在AQWA數值計算分析中，計算模型是以剛體結構考慮的，波浪作用于防波堤時，結構不會產生變形而消耗掉部分波浪能，以至于數值計算得到的消波效率較試驗結果普遍較小.

2.2 波高對防波堤消波效果的影響

通過計算波浪周期T=1.342 s不同布置方式下，不同波高對柔性浮式防波堤消波效果的影響曲線，發現隨著波高的增大，四種布置方式下防波堤的消波效率都有相對的減小，但差別不大，見圖9.在數值分析中，這主要因為AQWA的輻射衍射分析中求的解是單位波高的解，而后處理中是根據設置的不同波高值來乘以相應的系數.試驗中，由于測量和試驗中不可控制的外界因數，導致試驗結果個別點有些差異，但整體上變化趨勢與數值結果相同，隨著波高的增加，消波效率只是有相對的減小，但數值上相差不大.將數值計算結果與試驗結果比較分析發現，整體上數值結果與試驗結果具有較好的相關性，不同波高下數值計算得到的消波效率較試驗結果偏小，其誤差值在6%～15%.

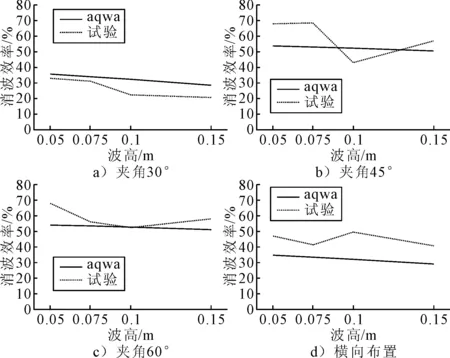
圖9 波高對消波效率的影響

2.3 布置方式對防波堤消波效果的影響

圖10～11分別為不同布置方式下波浪周期和波高對防波堤消波效果的影響曲線，從整體上看，在同等波浪工況下，V形布置防波堤的消波效果優于迎浪橫向布置防波堤的消波效果.V形布置防波堤在同波浪工況下，夾角為45°和60°的V形防波堤的消波效果優于夾角為30°的防波堤，夾角為60°的防波堤消波效果最好.V形布置的防波堤，在一定程度上對波浪起到了分離的作用，從而改變了波浪的傳播方向，實現對防波堤遮蔽區域的保護作用，以至于V形布置防波堤的消波效果比迎浪橫向布置較好.但同時由于夾角相對較小時，防波堤對波浪的分離較差，且波浪在防波堤端部引起的回流、湍流和紊流對遮蔽區域影響較大，導致小夾角防波堤的遮蔽區域以及堤后的消波效果相對較差.

圖10 不同布置方式下周期對消波效率的影響

圖11 不同布置方式下波高對消波效率的影響

3 實際模型計算分析

3.1 計算模型及計算工況

前面的試驗和數值仿真模型尺寸是根據實際結構按一縮尺比縮小得到的，針對工程實際應用的柔性浮式防波堤結構尺寸，建立其AQWA數值計算模型，計算分析實際結構尺寸及工況下柔性浮式防波堤的消波特性.根據國際通常的海洋工程試驗縮尺比60～80的原則，同時又為發揮拖曳水池的優勢、減小尺度效應以及方便實驗的實施，前面開展的實驗縮尺比λ設定的為20，進而根據縮尺比來確定的實驗模型尺寸，即：

式中：L，B，d，H，T分別為防波堤的長、寬、吃水以及波高和周期等波浪參數.

實際模型單個浮體總長80 m，下部水囊直徑8 m，上部氣囊直徑為2 m，結構吃水8 m，計算水深也按縮尺比λ進行縮放，實際模型計算水深為40 m，計算模型和錨泊纜繩布置情況見圖12.同時也分別計算了兩種布置方式，一種為V 形布置， V形的夾角分別為30°，45°和60°，另一種為單囊體迎浪橫向布置.

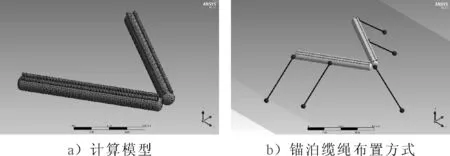
圖12 實體計算模型及錨泊纜繩布置情況

實體模型計算工況根據縮尺比換算得到，計算工況見表1.

表1 實體模型計算工況

3.2 計算結果及分析

進行實體模型的輻射衍射分析，通過AQWAGS得到實體模型的計算結果，圖13～14分別為45°夾角布置方式下V形柔性浮式防波堤在波高1.5 m和波浪周期6 s的規則波作用下，實體模型波高幅值云圖以及波幅隨入射波方向X軸的位置關系曲線.從計算結果可以看出，堤后的波幅值要明顯的小于堤前的波幅值，防波堤具有較好的消波效果，通過防波堤對波浪進行衰減后，堤后的波浪幅值逐漸趨于穩定，并且在其遮蔽區域消波效果較好.

圖13 實體模型波高幅值云圖

圖14 實體模型波浪方向波高幅值變化曲線

實體模型分別計算了波高1.5 m波浪周期T=5，6，7，8 s的不同布置方式下防波堤的消波效果，見圖15a)，與試驗模型數值計算結果相比，見圖15b)，從計算結果整體上看，實體模型數值計算結果與前面的試驗模型數值計算結果具有較好的相關性以及吻合性，除了橫向布置下的消波效果隨波浪周期的增加呈遞減趨勢，其它布置方式下消波效果隨波浪周期的增加呈現先增加后減小的趨勢，在周期T=6 s時的消波效果最好，而后減小.在夾角為30°和60°的布置方式下，實體模型計算結果與試驗模型數值結果吻合較好，可視為等效，其夾角45°和橫向布置方式的結果值雖然與試驗模型計算結果有一定的差異，但變化趨勢及規律總體相同.由于實體模型與試驗模型間的相關尺寸及載荷等參數是通過縮尺比換算得到的，其計算模型結構之間必然存在尺度效應，再加上計算工況以及錨鏈等參數間的換算等因數都對計算結果產生一定的影響.

圖15 不同布置波浪周期對消波效率的影響

同樣在實體模型中，計算了波浪周期為6 s，不同布置方式下不同波高對防波堤消波效果的影響曲線，見圖16a)，發現隨著波高的增大，四種布置方式下防波堤的消波效率都有相對的減小，但差值別不大，與試驗模型數值計算結果相似.同樣是因為AQWA的輻射衍射分析中求的解是單位波高的解，而后處理中是根據設置的不同波高值乘以相應的系數.

圖16 不同布置波高對消波效率的影響

通過圖15a)和圖16a)的實體模型在不同布置方式下消波效率隨波浪周期和波高的變化曲線可以看出，夾角為60°的V形柔性浮式防波堤的消波效果優于其它布置方式，在工程實際過程中，其為首先結構形式，并隨著夾角的減小，V形柔性浮式防波堤的消波效果也相應的降低.

4 結 論

1) 不同布置方式下柔性浮式防波堤的消波效率隨波浪周期的增加呈現先增加后減小的趨勢，防波堤對短周期波消波效果較好，在周期T=1.342 s時的消波效果最好.

2) 由于AQWA的輻射衍射分析中求的解是單位波高的解，而后處理中是根據設置的不同波高值乘以相應的系數，以至數值分析中波高對防波堤消波效果的影響較小，隨著波高的增大，其值只是相對的減小，但差值不大.

3) 數值模擬計算得到的消波效率較物理試驗結果普遍偏小，其誤差值在6%～15%.

4) 夾角為45°和60°的V形柔性浮式防波堤的消波效果優于夾角為30°和單一囊體迎浪橫向布置的柔性浮式防波堤，夾角為60°的防波堤消波效果最好.

5) 夾角為60°的V形柔性浮式防波堤的消波效果優于其他布置方式，在工程實際過程中，其為首先結構形式，并隨著夾角的減小，V形柔性浮式防波堤的消波效果有相應的降低.