基于PSO-LSSVM的礦井沖擊地壓分級預測研究

呂鵬飛，邱 林

(內蒙古科技大學 礦業研究院，內蒙古 包頭 014010)

沖擊地壓是自然地質因素與工程擾動因素耦合作用下的一種非線性煤巖動力響應[1]。近年來，隨著煤炭開采強度與深度增加，以沖擊地壓為代表的礦井動力災害發生的頻率和強度越來越大，因此在工作面開采之前實施必要的預測和防治措施對保障煤礦安全生產意義重大。以往的沖擊地壓預測主要以單因素預測方法為主，但日趨復雜的煤礦作業環境使單一指標預測法難以滿足沖擊地壓預測的準確性要求，數值模擬和相似材料模擬也不能完全真實反映現場情況。因此，一些學者提出沖擊地壓預測的多因素耦合智能算法，例如：陳剛等[2]構建了基于神經網絡與退火算法的沖擊地壓預測模型，這是國內較早的沖擊地壓智能預測模型；朱志潔等[3]針對ELM沖擊地壓預測模型中的權值誤差和隱含層偏差問題，將GA算法引入ELM模型中，提出了具有較高預測精度的GA-ELM預測方法；尹光志等[4]利用混沌算法優化了神經網絡模型，構建了沖擊地壓預測的CO-BP新模型；蘭天偉等[5]提出了礦井沖擊地壓模式辨識概率預測方法，準確性較高。

以上沖擊地壓預測方法雖有一定優勢，但可歸納出兩點不足：一是預測指標體系不完善，專家學者在預測中往往選擇對沖擊地壓影響較大的少數指標；二是多數算法要想獲得更高的預測精度，就需要較長的訓練時間，預測效率低。基于以上研究成果，綜合考慮沖擊地壓發生的10個典型影響因素，提出基于PSO優化LSSVM模型的沖擊地壓預測方法，該方法預測中只需優化LSSVM模型中的核參數σ和懲罰因子f，具有計算效率高、預測精度高、操作簡便等優點。

1 構建沖擊地壓分級預測指標體系

沖擊地壓危險等級劃分和分級管理對煤礦安全生產至關重要。按照微震等級將沖擊地壓危險等級劃分為5級：Ⅰ級為震級大于3.0級的沖擊地壓，屬于特別重大災害；Ⅱ級為震級2.0～3.0級的沖擊地壓，屬于重大災害；Ⅲ級為震級1.4～2.0級的沖擊地壓，屬于較大災害；Ⅳ級為震級0.6～1.4級的沖擊地壓，屬于一般災害；Ⅴ級為震級小于0.6級的沖擊地壓。不同等級的沖擊地壓災害是不同量級的沖擊地壓影響因素耦合作用的結果，故綜合考慮沖擊地壓影響因素是準確預測其危險程度的必要前提。預測指標如下：

1)開采深度：煤體承受自重能力與開采深度呈正比關系，故開采深度越大發生沖擊地壓的強度越高。

2)煤厚變化：煤層厚度變化位置的應力集中系數及彈性能都較大，因此沖擊地壓危險等級一定程度上取決于煤層厚度變化[6]。

3)最大主應力：最大主應力對沖擊地壓的發生具有控制作用，故礦井所處的構造應力場越強烈，表現出來的最大主應力對沖擊地壓發生的影響越嚴重[7]。

4)煤層傾角變化：煤層傾角變化反映煤層經歷的構造運動強度，煤層傾角變化劇烈的位置多是構造運動劇烈的位置，誘發沖擊地壓的可能性必然較大。

5)與斷層距離：斷層等地質構造對沖擊地壓起到一定控制作用，故斷層活化作用是誘發沖擊地壓的重要影響因素[8]。

6)頂板巖層厚度：頂板巖層厚度越大，斷裂釋放能量越大，發生沖擊地壓的危險程度越高[9]。

7)煤的堅固性系數：煤的堅固性系數是評價煤體抵抗載荷能力的重要指標，煤的堅固性系數越高，抗壓能力越強，煤體發生沖擊性破壞時釋放的能量越大。

8)開采工藝：開采工藝不同，沖擊地壓誘發作用也不同，炮采對圍巖擾動大于普采和綜采，放頂式開采對圍巖擾動大于一次采全高[10]。

9)頂板抗壓強度：頂板巖石強度越大，斷裂釋放的能量也越大，誘發沖擊地壓的概率越高[11]。

10)底板抗壓強度：底板巖層抗壓強度對底鼓型沖擊地壓發生起關鍵作用，底板巖石強度越大，底板鼓起和破壞釋放的能量越大[12]。

2 沖擊地壓分級預測原理

2.1 粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是在搜尋范圍內快速迭代尋求最優粒子的算法，并把尋優粒子當作優化問題的解。迭代過程中，兩個“極值”不斷變化，粒子隨之不斷更新，其中一個粒子作為已經搜索到的最優解p1，另一個粒子作為當前搜尋范圍內的種群最優解p2。粒子的位置和速度隨最優解不斷更新，最終找到符合條件的最優解[13]。粒子尋優方式如下：

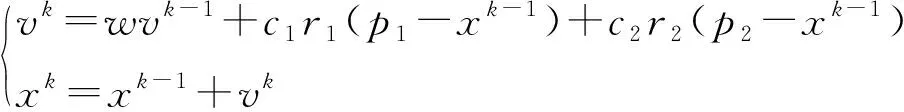
(1)

式中：vk為第k次偏移量；w為動量系數；c1、c2為搜索參數；r1、r2為修正系數；p1、p2為前后相鄰兩次迭代的最優解；xk為第k次迭代結果。

2.2 最小二乘支持向量機模型

最小二乘支持向量機(Least Squares Support Vector Machine，LSSVM)算法是對標準SVM算法的改進，LSSVM用等式約束和線性求解代替SVM中的不等式約束和非線性求解[14]，其算法過程如下：

假設有n個樣本，則LSSVM描述的問題為：

(2)

式中：J為目標函數；w為樣本權向量；ξ為樣本松弛變量；t為懲罰因子。

LSSVM的Lagrange方程為：

(3)

式中：b為算式偏置；α為Lagrange乘子；φ(xi)為樣本函數；xi為樣本，i=1，2，…，n。

通過參數求解可得LSSVM決策函數g(x):

g(x)=sgn[αK(σ,f)+b]

(4)

式中：K(σ,f)為滿足Mercer的核函數，K(σ,f)=φ(σ)φ(f)；σ、f為核函數的核參數和懲罰因子。

LSSVM核函數對預測模型起決定作用。選擇徑向基核(RBF)函數作為沖擊地壓預測的核函數，因為RBF函數結構簡單、泛化能力強，能夠滿足對核參數σ和懲罰因子f的快速尋優。

2.3 PSO-LSSVM模型的預測流程

直接影響PSO-LSSVM預測模型精度的是RBF核參數和懲罰因子的選取。PSO算法能快速找到最優的核參數和懲罰因子，減少了繁瑣的參數調整環節。PSO-LSSVM算法流程如圖1所示。

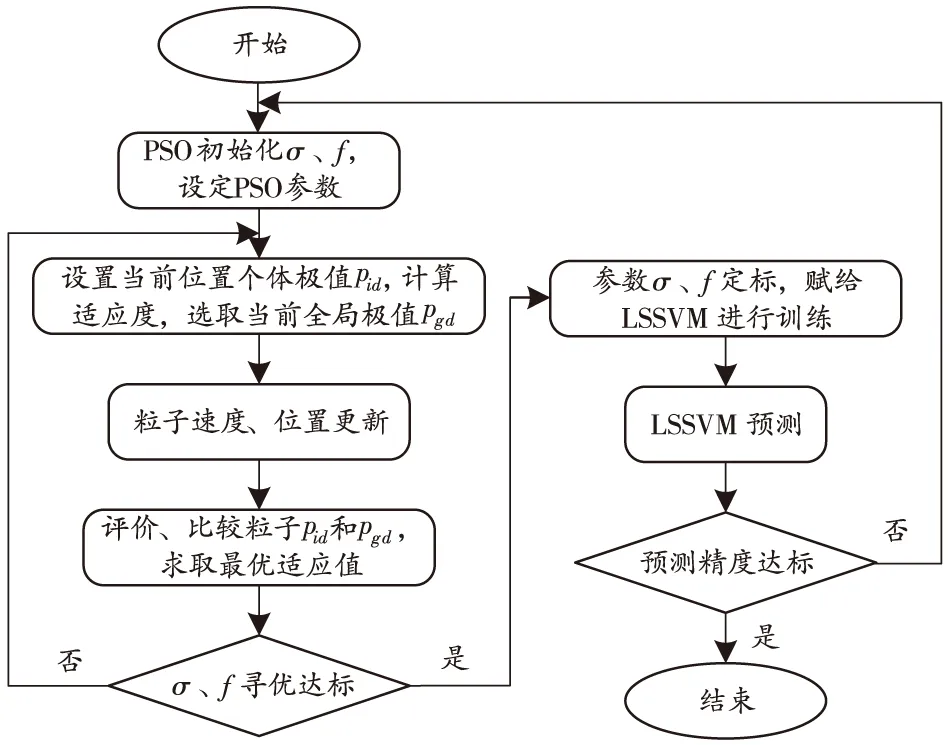
圖1 PSO-LSSVM算法流程

3 沖擊地壓分級預測實例

搜集多個礦區共計55組沖擊地壓歷史數據，從中隨機挑選40組數據作為本次預測的訓練樣本，其余15組數據為測試樣本。訓練樣本中1～6組數據采集于大安山煤礦中區后槽，該煤層為急傾斜煤層，位于向斜構造附近，多次發生煤炮等動力顯現；7～9組數據采集于木城澗煤礦+570 m水平，該區域為多煤層開采且間距小于30 m，頂底板為堅硬巖層，對煤層開采及巷道掘進影響較大；10～14組數據采集于忻州窯煤礦八采區，該區域煤層上覆留有煤柱，頂底板為堅硬巖層，具備較高的應力集中條件；15～19組數據采集于東灘煤礦六采區，該區域可采煤層范圍不連續，褶皺與斷層較發育，斷層落差最大超過 50 m；20～25組數據采集于鮑店煤礦十采區，該區域回采時先采上部3上煤層后采下部3下煤層，3下煤層回采時直接頂裂隙發育，局部破碎嚴重；26～30組數據采集于紅陽三礦西二采區，該區域開采深度超過1 000 m，頂板為堅硬特厚巖層；31～35組數據采集于紅陽三礦西一采區，該區域整體上為相對孤立的塊段，應力高度集中；36～40組數據采集于平頂山十礦二水平，該區域處于向斜構造軸部附近且斷層較多，頂板斷裂帶范圍較大，沖擊危險程度高。預測指標體系中，不能量化的指標采用數字處理，例如煤厚變化程度采用數字“1”“2”“3”分別表示煤厚變化大、一般和小；煤層傾角變化用“1”“2”“3”“4”分別表示煤層傾角變化程度劇烈、嚴重、一般和基本無變化；普采、炮采和綜采分別用“1”“2”“3”表示。訓練樣本和測試樣本數據如表1和表2所示。

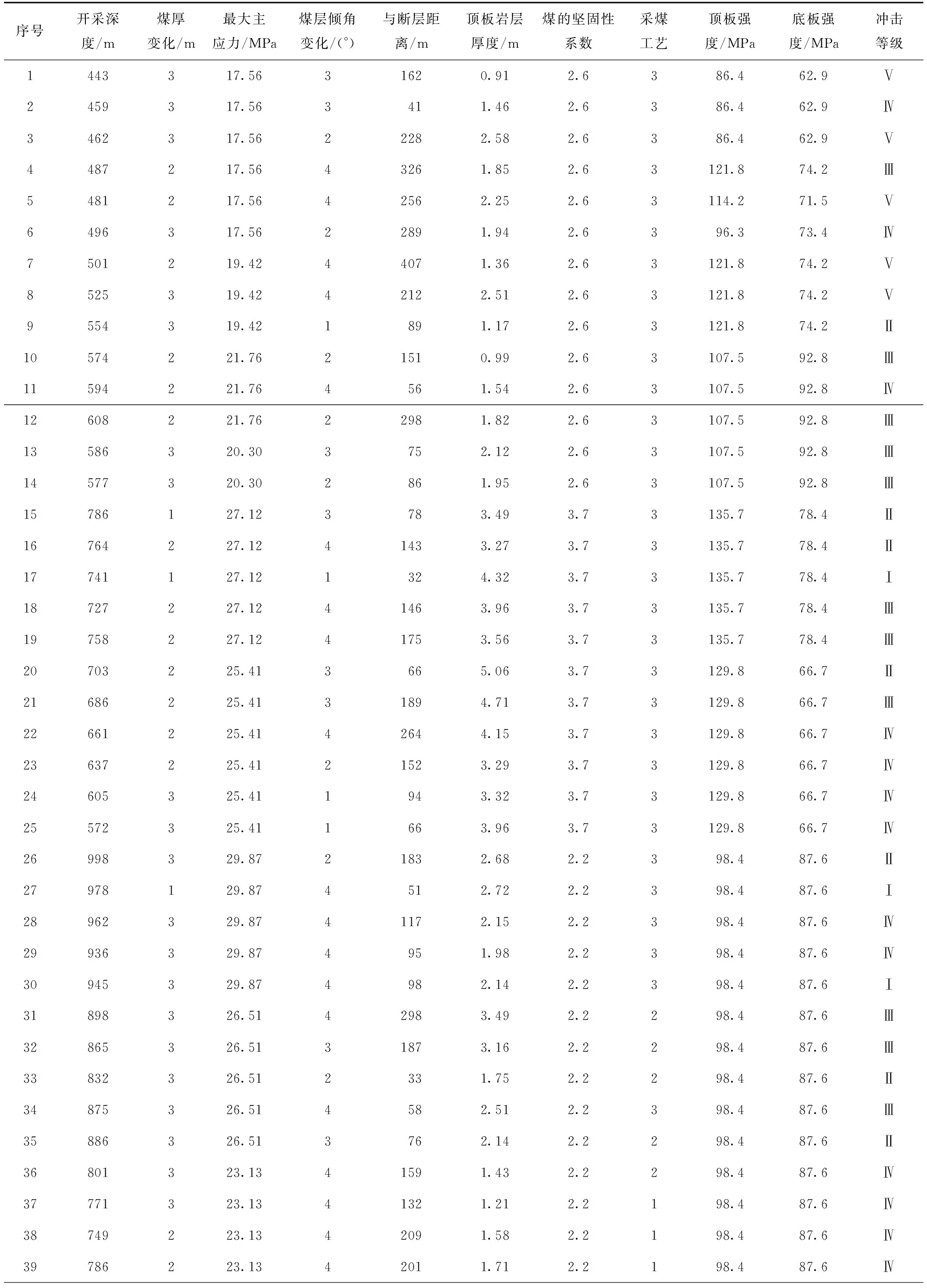
表1 訓練樣本數據

表1(續)序號開采深度/m煤厚變化/m最大主應力/MPa煤層傾角變化/(°)與斷層距離/m頂板巖層厚度/m煤的堅固性系數采煤工藝頂板強度/MPa底板強度/MPa沖擊等級40769223.1341591.622.2298.487.6Ⅲ

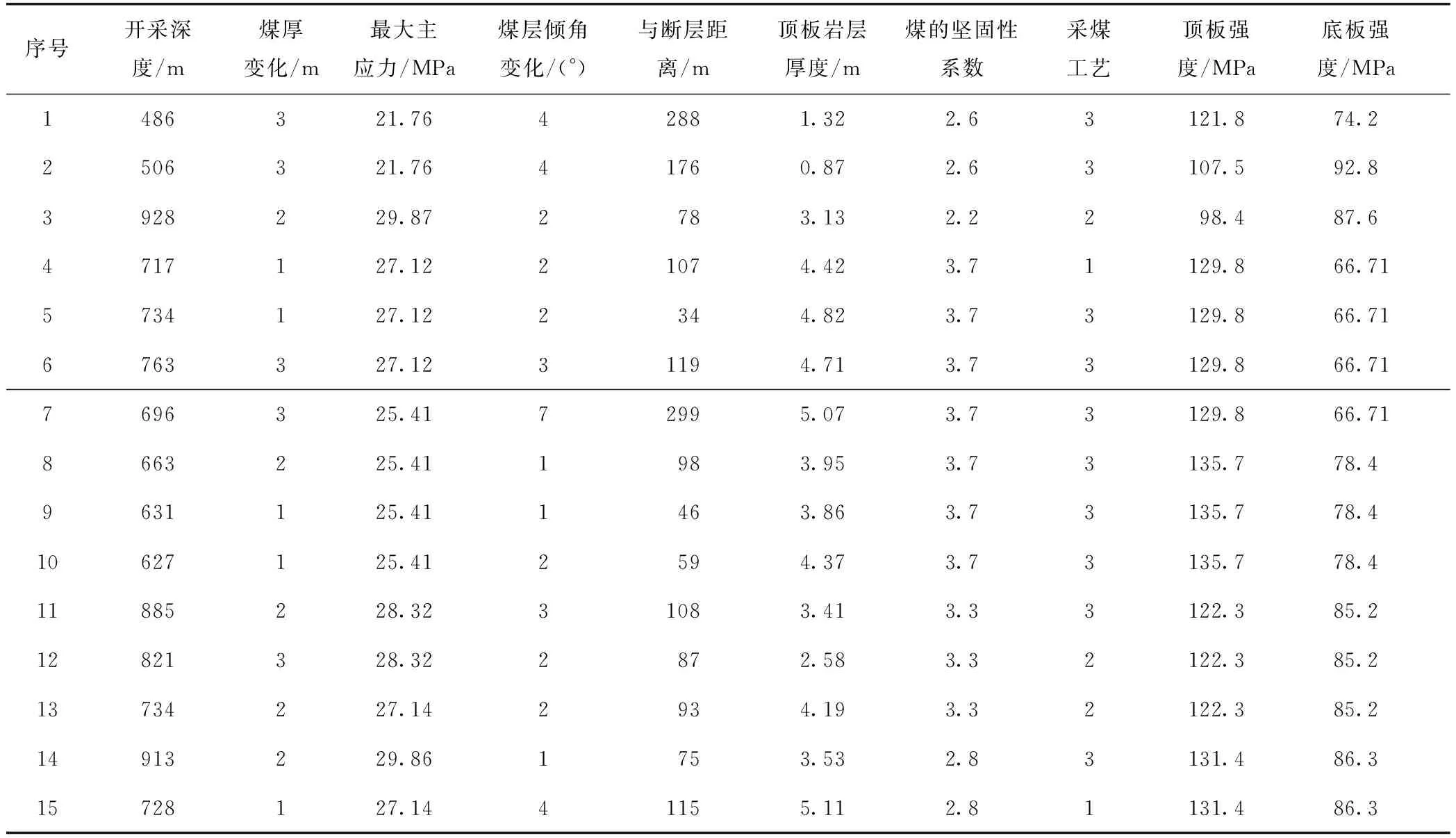
表2 測試樣本數據

采用MATLAB2014b軟件編寫PSO優化程序源代碼，借鑒文獻[15]所述的參數設定方法，本次預測中將PSO模型參數設定如下：設定粒子群規模m=20，粒子向量維n=2，搜索參數c1=1.5，搜索參數c2=2，迭代次數設置為100。經運算得到懲罰因子f=119.736 2，核參數σ=19.158 4。再將其輸入LSSVM模型中進行訓練，待訓練完成后將測試樣本數據輸入訓練好的LSSVM模型中進行預測，LSSVM預測模型主要程序代碼如下：

load data0.mat

[train_x,trps]=mapminmax(train_data′,0,1)

[test_x]=mapminmax(′apply′,test_data′,trps)

[train_y,tr1ps]=mapminmax(train_result′,0,1)

train_x=train_x′;train_y=train_y′

test_x=test_x′;bestmse=0.1

type=′f′;gam=500;sig2=0.45

kernel =′RBF_kernel′;proprecess=′proprecess′

model=initlssvm(train_x,train_y,type,gam,sig2,kernel,proprecess)

model=trainlssvm(model)

[train_predict_y,zt,model]=simlssvm(model,train_x)

train_predict=mapminmax(′reverse′,train_predict_y,tr1ps)

test_predict=mapminmax(′reverse′,test_predict_y,tr1ps)

trainmse=sum((train_predict-train_result).^2)/length(train_result)

testmse=sum((test_predict-test_result).^2)/length(test_result)

PSO-LSSVM模型預測結果如圖2所示。可以看出，測試集預測結果與真實結果完全吻合，誤判率為0，說明基于PSO-LSSVM的沖擊地壓分級預測方法準確率較高。

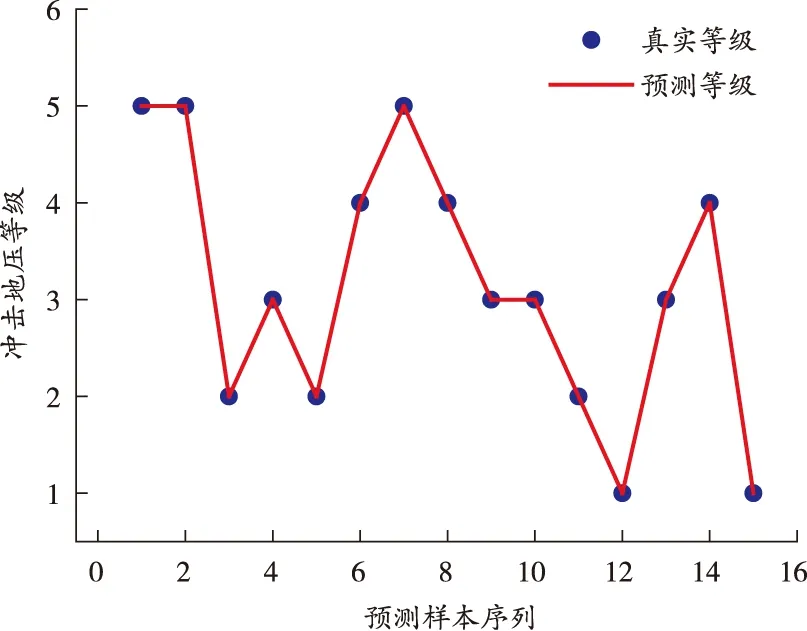
圖2 PSO-LSSVM預測結果

為進一步確定PSO-LSSVM方法的準確性和實用性，將PSO-LSSVM方法的預測結果與BP、SVM、LSSVM和GA-LSSVM方法的預測結果進行對比，如表3所示。

表3 預測結果對比

由表3可以看出，PSO-LSSVM預測未出現誤判情況，其他4種預測方法都有一定的誤判率，其中GA-LSSVM方法誤判率為20%，LSSVM算法誤判率為33%，SVM算法和BP算法的誤判率都為47%。此外，PSO-LSSVM算法操作簡便，只需將預測區指標參量輸入模型，即可得到結果。實例分析表明，沖擊地壓分級預測的PSO-LSSVM方法最優。

4 結論

1)分析了沖擊地壓影響因素，提取10項對沖擊地壓發生起關鍵作用的影響因素，建立了沖擊地壓預測指標體系。

2) 采用PSO優化了LSSVM模型中的核參數和懲罰因子，在此基礎上提出了沖擊地壓預測的PSO-LSSVM方法，并進行了實例預測。

3) 將沖擊地壓預測的PSO-LSSVM方法與BP、SVM、LSSVM、GA-LSSVM方法的預測結果進行了對比，表明PSO-LSSVM方法相較其他同類方法具有更高的預測精度。