利用灰色殘差GM(1,1)-Markov模型預測水工混凝土的劣化

康春濤，貢 力, ，王忠慧，楊軼群，王 鴻

(1. 蘭州交通大學 土木工程學院，甘肅 蘭州 730070；2. 蘭州交通大學 調水工程及輸水安全研究所，甘肅 蘭州730070)

我國西北干寒地區具有冬長暑短、雨熱同季、日照時間長、年降水少、蒸發量、晝夜溫差大和年季溫差較大的高寒半干旱氣候特點。據水利部資料統計，我國西北地區混凝土水工建筑物70%的破壞受損都與地區的嚴寒氣候有關[1-2]。大多數水工混凝土建筑物出現剝蝕甚至脫落現象。因此，對水工混凝土建筑物劣化預測模型的研究，對于水工建筑物的結構安全和壽命維護具有重要的意義。

目前，對于混凝土劣化預測的方式有很多種。肖前慧等[3]提出了凍融循環下混凝土抗壓強度指數衰減規律預測模型和壽命預測模型；馮忠居等[4]基于灰色系統理論，建立了不同工況下混凝土相對動彈性模量GM(1,1)預測模型；鄔曉光等[5]利用可拓評價模型實現對混凝土梁式橋耐久性的預測；胡宸瑞[6]采用Wiener分布模型對其在不同環境因素下的服役壽命進行預測；馬俊軍等[7]在Fick第二定律的基礎上，建立了考慮氯離子隨機擴散效應的元胞自動機模型等。劉榮桂等[8-10]諸多專家在理論上對混凝土耐久性的預測提出了創新方法。近年來，眾多專家在灰色理論的基礎上，提出了殘差模型和馬爾科夫（Markov）理論相結合的預測方法[11-12]。張克中等[13]在灰色殘差基礎上提出馬爾科夫殘差修正灰色模型，并將其應用于公路網規劃中運輸量的預測；陳佳琪等[14]采用傳統GM(1,1)模型和改進后的殘差修正GM(1,1)模型分別對房屋建筑面積統計數據進行預測；杜永強等[15]以最大延伸率作為性能變化表征參數，根據老化反應速率常數隨溫度的變化關系，建立了馬爾科夫灰色殘差GM(1,1)模型，對常溫條件下推進劑的老化反應速率常數進行了預測。通過結合灰色殘差和馬爾科夫模型，不僅讓兩個模型能體現各自的優點，而且能彌補數據信息波動性大的不足，能更好地提高預測模型精度[16]。目前，針對混凝土劣化的預測模型，大多數集中在公路、橋梁及房建等混凝土建筑物，對于西北干寒地區水工建筑物的研究較少；另外，基于灰色殘差GM(1,1)-Markov模型在水工混凝土劣化預測方面的研究較少。

本文將灰色殘差GM(1,1)的馬爾科夫模型應用于水工混凝土建筑物劣化試驗預測，通過實驗室方法來驗證預測模型的適用性。首先對混凝土試件進行耐久性劣化試驗，以質量和抗壓強度的原始值作為初始數據，通過一系列數據處理，得到灰色GM(1,1)模型和殘差GM(1,1)模型。然后利用馬爾科夫過程的符號修正，對灰色殘差GM(1,1)模型進行馬爾科夫修正，以此來預估混凝土試件在鹽凍作用下的壽命。

1 利用GM(1,1)模型預測強度或質量損失

1.1 灰色GM(1,1)模型

參考郭鵬等[17-18]的理論，本文對灰色GM(1,1)模型的建立過程是將混凝土劣化的質量損失和抗壓強度損失過程累加生成數列模型，再將數列模型進行處理，最終得到預測值。用X(0)(k)表示劣化試驗壽命的原始數據序列，設原始數據為：

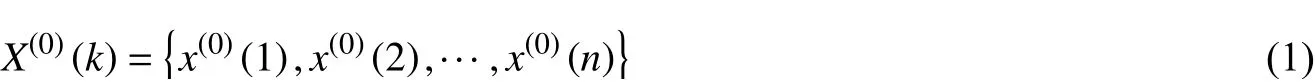
對X(0)(k)做一次累加生成算法，生成一階累加生成數列：

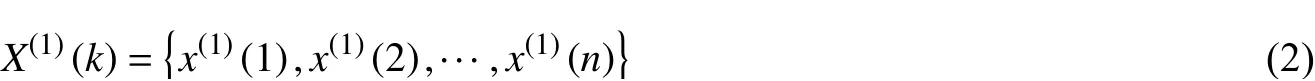
由式（2），計算得到x(1)(k)的緊鄰均值系列Z(1)，Z(1)={z(1)(2), z(1)(3),···, z(1)(n)}，其中：

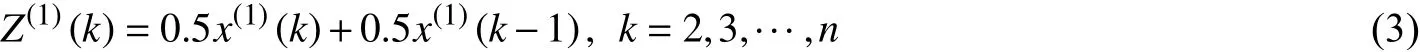
構建微分方程dx(1)/dt+αx(1)=β，其中，參數α、β可由下式得到：

求解上述微分方程，得到如下GM(1,1)模型：

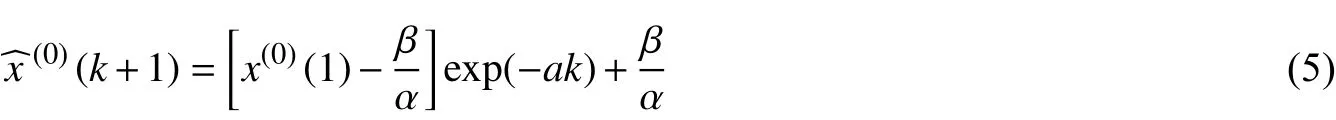
用如下累減公式還原，即可計算出預測值：

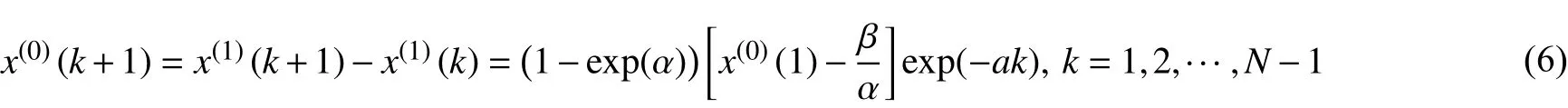
式中：x(0)(k+1)為第（k+1）項的預測值；x(0)(1)為原始數據序列的首項；α、β分別為GM(1,1)模型的系數和常數項，由最小二乘法（回歸）求得。

1.2 灰色殘差GM(1,1)模型

為了修正預測值與混凝土劣化試驗初始值結果的差異，建立殘差序列ε1(0)，ε1(0)={ε1(0)(2), ε1(0)(3),···,ε1(0)(n)}，其中：

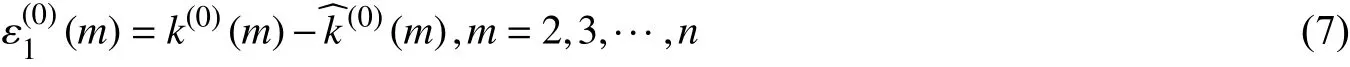
對得到的ε(0)按式（2）～（6）的步驟建立灰色GM(1,1)模型，可得：

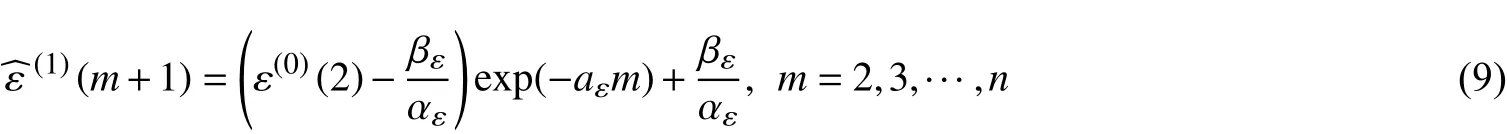
其中，參數aε、bε按照式（4）求解，則殘差修正值為：

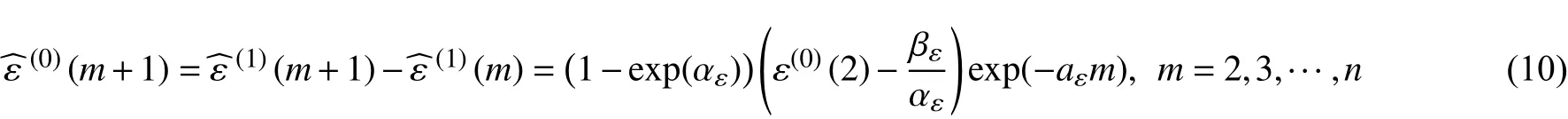
用得到的殘差修正值 修正還原值x(0)，得到：

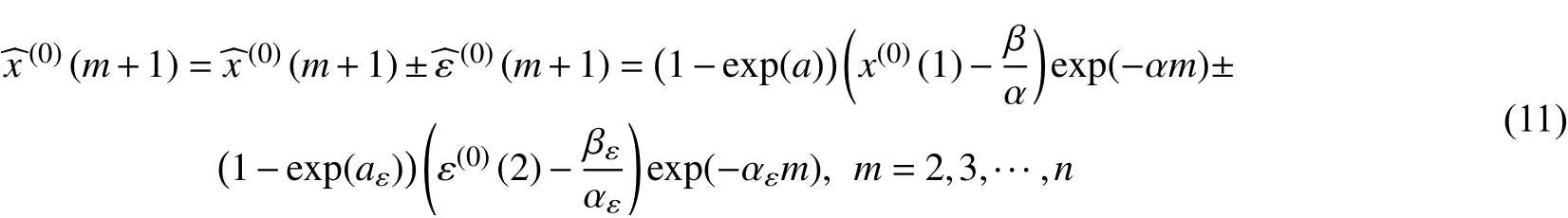
1.3 馬爾科夫過程的符號修正

由于預測模型僅是對原始數據的規律總結，可能會導致原始數據與預測數據的相對誤差較大，因而有必要對模型進行改進。故本文將灰色殘差GM(1,1)和馬爾科夫模型應用于水工混凝土劣化試驗的預測中，以提高預測模型的精度[19]。

統計殘差序列的頻數，規定狀態：殘差正值為狀態1，殘差負值為狀態2。根據其狀態的正負，得到狀態轉移概率矩陣如下：

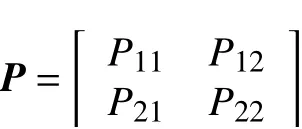
把殘差從狀態i轉移到狀態j的概率記為Pij，例如，P12代表從狀態1轉移到狀態2的概率，Pij≥0，且可由下式確定：

式中：sij為狀態i轉移到狀態j的次數；si為狀態i出現的次數。

其余計算過程參考文獻[18]，此處不再贅述。

由下式計算相對誤差：

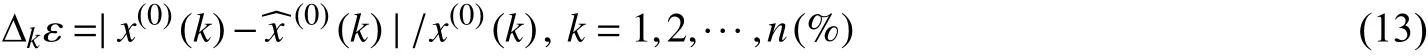
2 試驗數據處理及壽命預估

2.1 數據來源與試驗設計

參考《普通混凝土長期性能和耐久性能試驗方法標準》，試驗采用慢凍法。采用100 mm×100 mm×100 mm立方體標準試件，試件設計抗凍標號為D200，試件規格強度為C30的試件，共120塊，其中水泥型號為甘肅省祁連山水泥集團股份有限公司生產的P·O 32.5水泥。另外，考慮細骨料和粗骨料中的含水量（分別為2.4%和1.0%），混凝土材料組成見表1。

表 1 混凝土材料組成Tab. 1 Concrete mix proportion

試件成型后拆模，在養護箱中養護至28 d齡期。試件分為4個部分，每部分為30塊。參考普通混凝土長期性能和耐久性能試驗方法標準，在試驗前4 d把試件從養護地點取出，分別置于清水及質量濃度為3、5和7 g/L的Na2SO4溶液中進行浸泡，對應試件分類編號為：1-0、1-3、1-5和1-7。

將經過浸泡的試件按照其分類，進行鹽凍試驗，每25次小循環之后，清理試件上的碎渣，并及時稱量，用軸心抗壓試驗儀進行抗壓試驗，計算質量損失率及抗壓強度損失率。當質量損失率達到5%，或抗壓強度損失率達到25%或達到鹽凍試驗次數（根據設計抗凍標號，其次數為200～250次），可認定為達到破壞條件，結束試驗。

2.2 數據處理

限于篇幅，本文抽取清水和3 g/L硫酸鈉溶液侵蝕的試件質量和抗壓強度損失統計數據進行計算。水工混凝土在鹽凍作用下，試件質量和抗壓強度隨著次數的提高而減小，具體數據見表2。

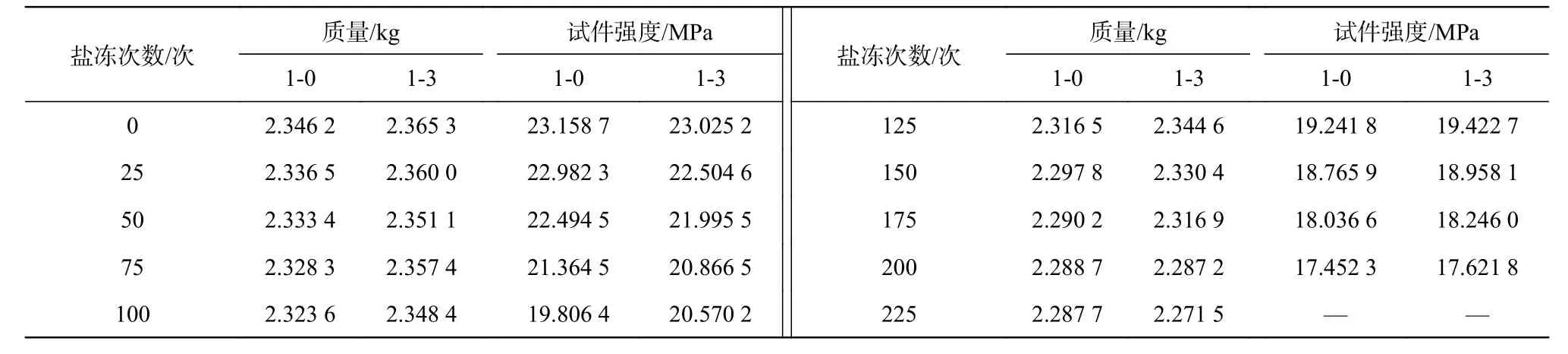
表 2 鹽凍作用下混凝土試件質量和抗壓強度原始統計值Tab. 2 Original statistical values of the quality and pressure strength of concrete specimens under the action of salt freezing

以清水浸泡過的混凝土試件為例，計算原始質量的灰色模擬值和殘差模擬值如下。本文0～125次鹽凍試驗的質量作為原始值，預測150～200次的數據。原始數據及預測結果見表3。

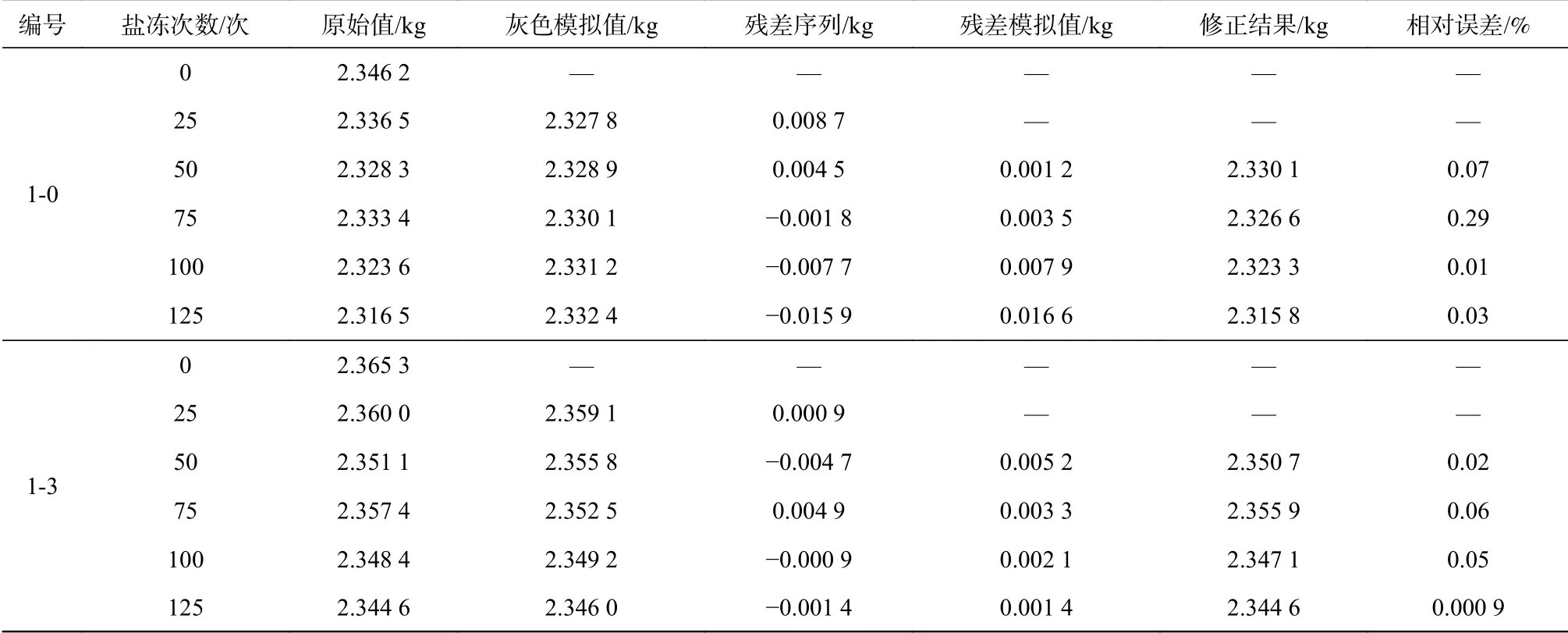
表 3 混凝土試件質量的模擬結果Tab. 3 Simulation results of the quality of concrete specimens

由表3可知，基于馬爾科夫的GM(1,1)模型的模擬結果中，經過清水浸泡和鹽凍試驗的混凝土試件質量的最大誤差為0.29%，最小誤差為0.01%，平均誤差為0.10%；經過3 g/L硫酸鈉溶液浸泡和鹽凍試驗的混凝土試件質量的最大誤差為0.20%，最小誤差為0.000 9%，平均誤差為0.03%。

由模擬結果可見，灰色GM(1,1)模型的質量模擬結果誤差較大（1-0和1-3的最大相對誤差分別為0.37%和0.21%），但是灰色殘差GM(1,1)模型經過殘差修正之后，相對誤差明顯降低（1-0和1-3的最大相對誤差分別為0.33%和0.06%）。

相應地，可計算出經過清水浸泡和鹽凍試驗的混凝土試件抗壓強度模擬結果見表4。

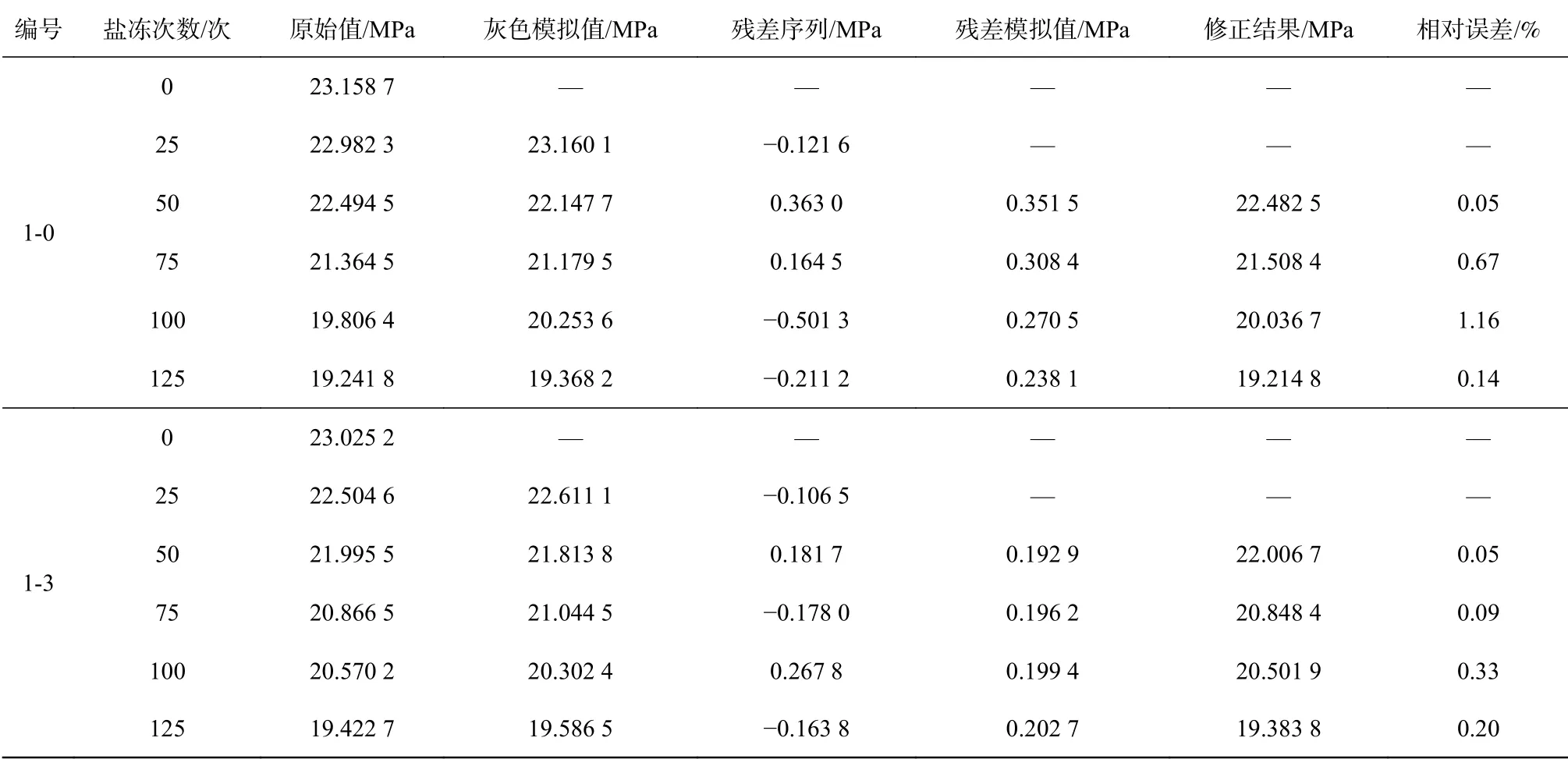
表 4 混凝土試件抗壓強度的模擬結果Tab. 4 Simulation results of the pressure strength of concrete test pieces

由表4可知，基于馬爾科夫的GM(1,1)模型的模擬結果中，經過清水浸泡和鹽凍試驗的混凝土試件抗壓強度的最大誤差為1.16%，最小誤差為0.05%，平均誤差為0.51%；經過3 g/L硫酸鈉溶液浸泡和鹽凍試驗的混凝土試件抗壓強度的最大誤差為0.33%，最小誤差為0.05%，平均誤差為0.165%。

在不同濃度下，灰色GM(1,1)模型的抗壓強度模擬得出：1-0和1-3系列最大相對誤差分別為2.53%和1.30%。經過灰色殘差GM(1,1)模型修正之后，1-0和1-3系列最大相對誤差分別降為1.16 %和0.33%。相對誤差的變化，可以證明經過修正的灰色殘差GM(1,1)模型對抗壓強度的模擬效果要比灰色GM(1,1)模型好。

通過以上計算分析得出：相對于灰色GM(1,1)模型，殘差修正GM(1,1)模型能更好地貼合原始數據的質量損失和抗壓強度損失過程。所以，此模型可用于現有的數據預測，并對現有數據的規律得出預測模型經驗公式。

2.3 符號修正

由于第225次鹽凍試驗的試件抗壓強度已失效，故本文應用灰色殘差GM(1,1)模型，僅對清水及濃度為3 g/L的硫酸鈉溶液侵蝕的混凝土試件的150、175、200次鹽凍試驗的質量和抗壓強度進行預測，并確定殘差修正值的符號。

根據表3混凝土試件質量的模擬結果，對150次鹽凍試驗的質量預測如下：

根據馬爾科夫過程的符號修正，殘差由正數向正數轉移的次數是1，正值出現的次數是2，因此，其概率P11=1/2，同理可得P12=1/2、P21=1/3、P22=2/3。由此可得馬爾科夫狀態轉移矩陣P為：

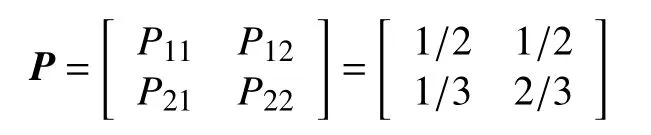
將鹽凍試驗125次的混凝土質量作為初始狀態，由表3知其殘差值為負，因而初始向量s(0)=(0,1)。由式（13）得到第150次鹽凍試驗的結果為：

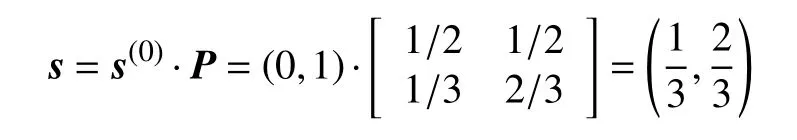
即第150次鹽凍試驗的混凝土質量殘差修正值為正的概率為1/3，為負的概率為2/3，因此取正號。預測150次鹽凍試驗的質量見表5。以150次鹽凍試驗的質量殘差修正值為初始值，同理可得出175、200次質量的預測值。同理可得3 g/L硫酸鈉溶液侵蝕的混凝土試件的質量（表5）。

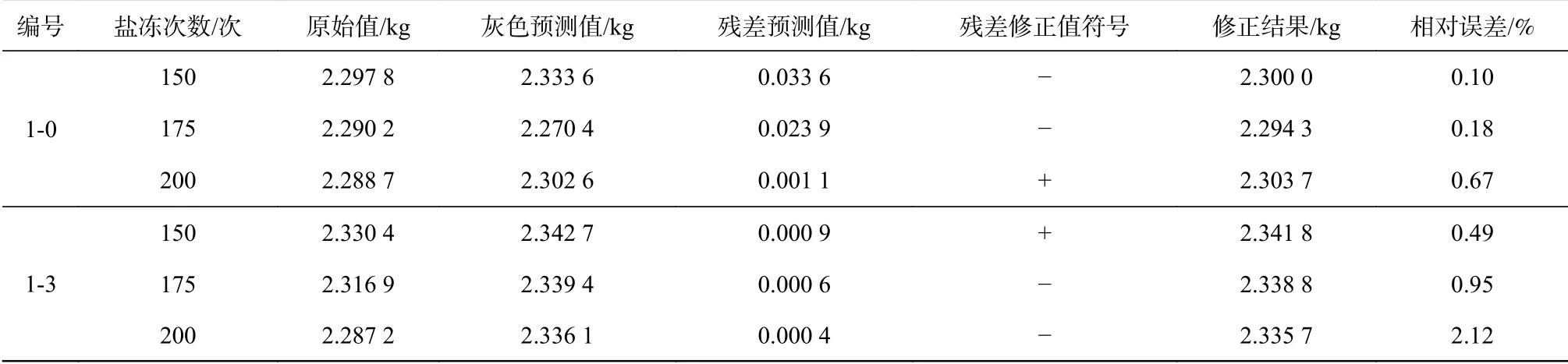
表 5 混凝土試件質量預測結果Tab. 5 Prediction results for the quality of concrete test pieces

由表5可知，通過Markov模型的符號修正，在不同硫酸鈉溶液濃度下水工混凝土試件150～200次鹽凍試驗的質量原始值與預測值，最大誤差為2.12%，最小誤差為0.10%，且相對誤差隨著鹽凍試驗次數的增加而變大。

同理，可得清水和3%硫酸鈉溶液浸泡侵蝕的混凝土試件的抗壓強度預測值，見表6。

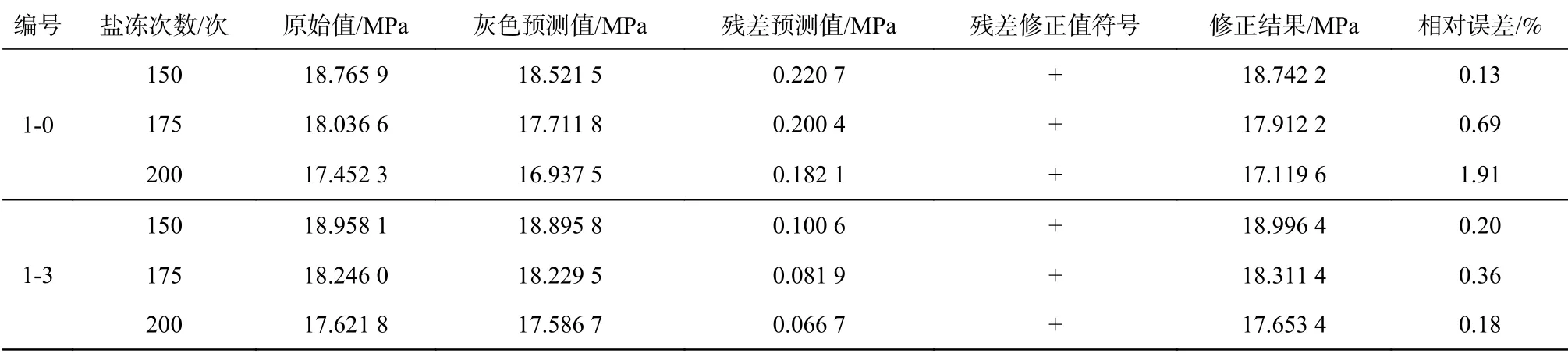
表 6 混凝土試件抗壓強度預測結果Tab. 6 Prediction results for the strength of resistance of concrete test pieces

由表6可知，混凝土試件在鹽凍試驗下，抗壓強度預測值的最大誤差為1.91%，最小誤差為0.13%。由于馬爾克夫符號修正預測序列較長，相對誤差略有偏大，但總體來看屬于正常誤差范圍，符合預測模型對于誤差的要求。這表明該模型對于混凝土劣化過程預測具有較好的適用性。

對比質量和抗壓強度的初始值、灰色GM(1,1)模型計算值、灰色殘差GM(1,1)模型計算值、馬爾科夫過程符號修正計算值見圖1。如圖1所示，由于質量的單位基數較小，使得質量預測的相對誤差較為明顯。

根據最初的灰色GM(1,1)模型的預測，并對此模型進行殘差修正，得到灰色殘差GM(1,1)模型。通過與初始數據的對比，可以發現灰色殘差GM(1,1)模型精度有了明顯提高。最后，利用馬爾科夫過程的符號修正，對混凝土試件150～200次鹽凍試驗的試件質量損失和抗壓強度損失進行預測，使得預測結果更符合實際情況，為混凝土水工建筑物的劣化預測指標提供理論支撐和技術保障。

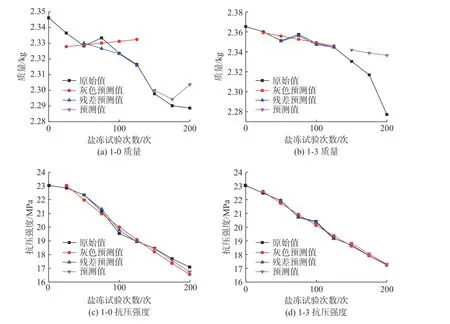
圖 1 數據修正與模型預測對比Fig. 1 Data correction and model prediction comparison chart

3 結 語

（1）以灰色GM(1,1)模型為基礎，經過數據累加生成數列模型，依次得到灰色GM(1,1)預測模型和灰色殘差GM(1,1)預測模型。通過殘差值的頻數統計得到狀態轉移矩陣，并對預測數據的符號進行修正，得到了灰色殘差GM(1,1)-Markov模型。

（2）借助灰色殘差GM(1,1)-Markov模型對經過鹽凍試驗的水工混凝土試件的質量和抗壓強度進行預測，結果表明：質量和抗壓強度的預測值與原始值相比誤差較小，最大誤差為2.12%，最小誤差僅為0.13%。驗證了在一定的預測范圍內，該模型對混凝土劣化的質量和抗壓強度損失具有很好的預測效果。