Python可視化電磁波在各向異性材料中的折射

張曉燕

（華北科技學院理學院 北京市 101601）

1 引言

近30年來，計算機已經發展成為現代技術的基礎構件，Python 以其簡潔和面向生態的設計理念得到廣泛認同，形成了全球范圍最大的單一語言編程社區[1]。Python 能夠將數學、自然科學、工程基礎和專業知識用于解決復雜工程問題，能夠基于科學原理和科學方法設計實驗、分析解釋數據、描繪圖像，學科與編程的結合成為了應對科學挑戰的重要橋梁[2]。

近年來人工超材料表現出負折射、旋光性、逆多普勒效應等獨特性質[3]，引起了學術界的積極關注。由于各向異性材料的介電常數和磁導率在各方向上是不同的，所以能實現更多電磁特性，具有更廣泛的應用[4]，如電磁隱身、波導、偏振轉換等。單色平面波在各向異性材料中的色散方程隨介電常數和磁導率的符號不同會有不同的形式，我們使用Python3.8 編程，調用Matplotlib 庫畫出不同參數對應的三維色散曲面圖。某些情況下波矢量和坡印廷矢量會出現負折射現象，我們畫出了二維情形下的色散曲面和波矢量、坡印廷矢量的折射方向，使得折射性質更形象的體現出來。

2 色散方程

圖2：雙雙曲面型色散關系

2.1 波矢曲面為單雙曲面

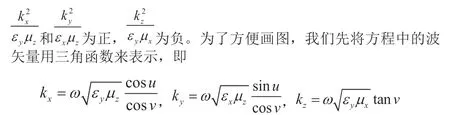
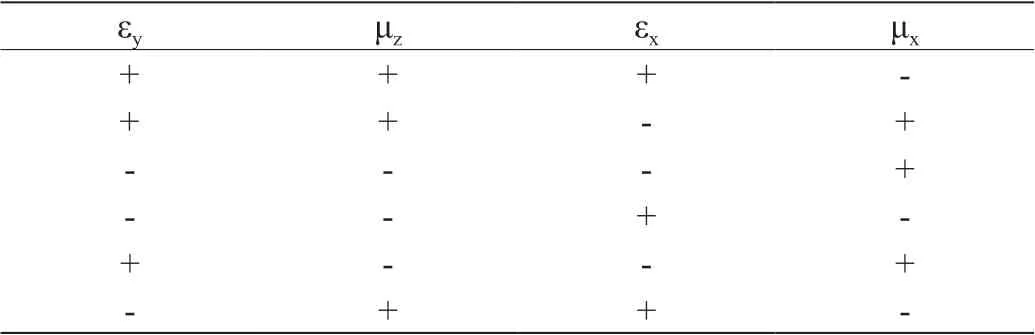
表1：單雙色散曲面對應參數符號

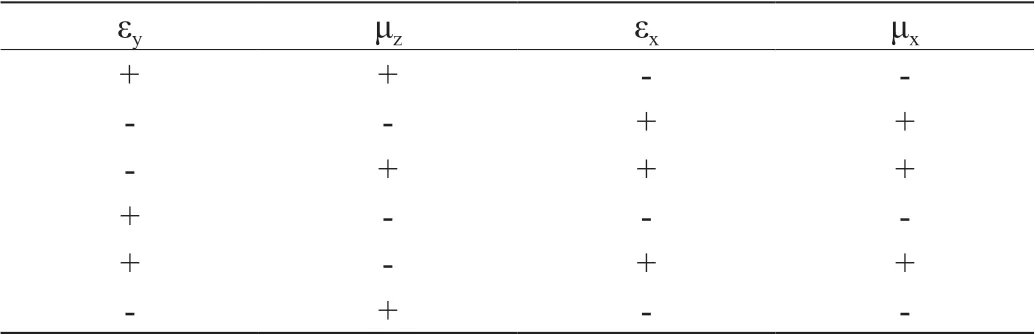
表2：雙雙色散曲面對應參數符號

表3：橢球色散曲面對應參數符號

圖3：橢球曲面型色散關系

然后調用Matplotlib 數據庫畫出三維曲面（圖1），涉及到的數值計算和公式表達用到了NumPy 庫，用meshgrid 函數使兩個坐標軸上的點在平面上畫網格，從而形成三維曲面圖。使用ax.plot_surface 函數形成著色圖，用rstride 和cstride 參數控制網格線的數量，用cmap 參數配色。

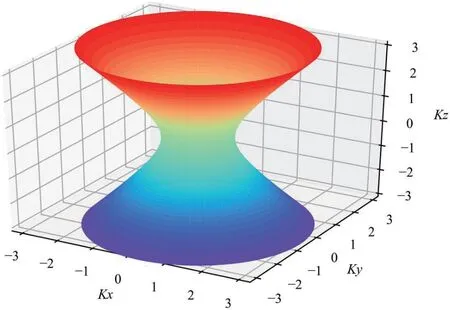
圖1：單雙曲面型色散關系

2.2 波矢曲面為雙雙曲面

2.3 波矢曲面為橢球曲面

3 各向異性材料中波矢量和坡印廷矢量的折射

Smith 等人把各向異性材料分為四種類型：Cutoff、Antcutoff、Never cutoff和Always cutoff。依據我們上面（9）（10）式的結論，我們將四種材料對應的波矢量和坡印廷矢量的折射性質列于表4 中，并依據（9）式計算結果為實數可以得出全反射條件。依據（9）（10）式，在45°入射角的情況下可以算出透射方波矢量和坡印廷矢量的折射角。我們通過調用Matplotlib 庫畫出了三種各向異性材料的色散曲線和波矢量和坡印廷矢量的折射情況（如表5）。其中二維色散曲線主要使用了Matplotlib 的plot 功能，帶箭頭的入射和折射光線主要應用了annotate 函數。圖4 是表5 中εy、μz>0，μx<0 參數下的圖像對應的主要程序代碼，其它圖像的程序與之類似，只是變換了annotate 函數中的起點和終點坐標。

表4：各向異性材料波矢量和坡印廷矢量折射性質及全反射條件

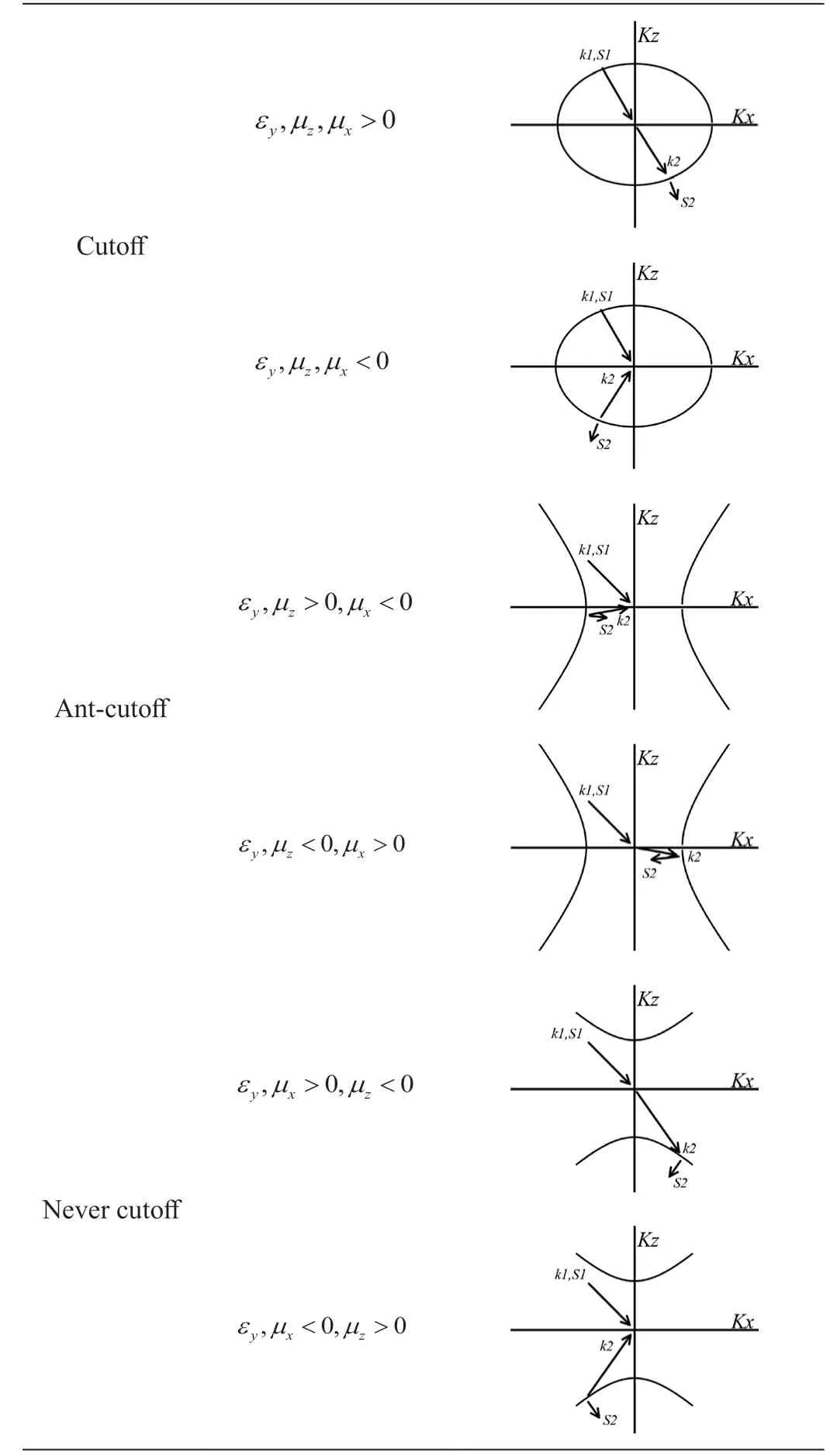
表5：各向異性材料色散關系及波矢量和坡印廷矢量的折射

圖4：Ant-cutoff 材料色散曲線及波矢量和坡印廷矢量折射圖的部分python 代碼（參數εy=0.7,μz=0.8,μx=-1.1）

4 結束語

現階段Python 已經成為社會各個領域重要的編程語言，它擁有強大的第三方庫，使用時可以直接調用，從而能簡單、準確的完成計算和繪圖工作。同時它免費、開源，容易掌握，是一門終身受益的編程語言。上面我們用Python 畫出了各向異性材料中的三維色散關系，描繪了二維情形下TE 波在各向異性材料中的色散曲線、波矢量和坡印廷矢量的折射方向，使得各向異性材料中的特異現象更形象的表現出來，體現了Python 用于科學計算的優越性。