基于精確罰函數的無人艇航跡規劃和自動避障算法

李清亮，李彬，孫國皓，崔星，毛新濤

1 四川大學 電氣工程學院，四川 成都 610065

2 四川大學 空天科學與工程學院，四川 成都 610065

3 北京軒宇空間科技有限公司，北京 100194

0 引 言

近年來，無人駕駛受到日益廣泛的關注，在飛行器、智能車、艦船等領域得以快速發展。智能化是未來艦船的發展趨勢之一[1]。由于無人艇的制造成本低、制造周期短、環境適應能力強、人力成本低，其在海洋資源勘測、航道測量、環境監測、水域清潔、軍事作戰等領域具備良好的應用前景。如何快速生成無人艇在復雜環境下的避障航線，是其自主化發展的關鍵技術之一[2]。

李文華等[3]總結了在工業4.0 背景下世界范圍內船舶自主化航行技術的主要發展路徑，分析了無人艇航跡規劃、智能避障等關鍵技術。余必秀等[4]通過增加代價函數從而改進了傳統的A*算法，可用于規劃無人航道測量船的運動路徑。Song 等[5]提出了平滑的A*算法來減少冗余的路徑點，從而可以提供更連續的路徑。Liu 等[6]提出了一種基于快速步進（fast marching，FM）方法的無人艇信息導航路徑規劃算法，具有計算速度快、計算復雜度低等特點，該算法覆蓋了2 個區域（航行區域和避碰區域），可以保證規劃軌跡不違反任何禁區。Cho 等[7]在改進現有視線（line-of-sight，LOS）制導算法和速度障礙（velocity obstacle，VO）制導算法的基礎上，提出了航點跟蹤與避碰算法：即在路徑點轉換過程中引入額外的控制方案以提高跟蹤控制的穩定性，并對傳統的VO 算法進行改進，從而有效解決了遇到障礙物時的位置不確定性問題，同時在真實海洋環境下驗證了算法的有效性。歐陽子路等[8]將雙向搜索 樹（bidirectional rapidly-exploring random trees，Bi-RRT）算法與速度障礙法相結合，提出了基于改進Bi-RRT 的無人艇自動避碰算法，并采用并行延伸擴展的2 顆搜索樹提高了算法的實時性。受人工智能技術的影響，很多智能算法已在無人艇路徑規劃領域得以運用，如粒子群算法[9]、蟻群算法[10]、強化學習[11]、人工神經網絡[12]等。舒宗玉[9]提出了多目標優化混合粒子群路徑規劃算法，實現了無人艇路徑長度、路徑平滑性和安全性的多目標優化。邱晨等[10]基于改進的蟻群算法，規劃了無人救生艇的最短無碰撞安全路徑。沈海青[11]將A*并行決策動態避障算法與基于深度Q 學習的智能避碰算法相結合，為無人艇提供了多層避碰導航。魏新勇[12]利用卷積神經網絡技術識別附近水域的障礙物，并結合模糊數學理論構建了危險系數指標，提出了遠程航跡重規劃和近程反應式避障方法。

障礙物的存在為航跡規劃帶來了巨大的挑戰，其中障礙物處理的難易程度直接決定了航跡優化問題的復雜程度，而現有文獻對障礙物的處理方法普遍比較復雜。為此，本文擬采用圓形包絡面和凸四邊形包絡面對障礙物進行包絡處理，并將避障問題轉化為在笛卡爾坐標系下的不等式約束問題；通過引入精確罰函數，以簡化處理多個障礙物帶來的多個強制約束問題。同時，鑒于現有研究成果在航跡規劃方面鮮有考慮無人艇的運動特性，本文擬基于無人艇的運動方程，采用控制參數化方法求解時間最優的控制問題；通過結合控制參數化方法與精確罰函數方法，較好地處理無人艇的航跡規劃和自動避障問題，并采用仿真驗證本文方法的有效性。

1 問題模型

1.1 無人艇運動學建模

為簡化處理，本文將無人艇視為僅規劃其運動航跡的質點，其運動學坐標系如圖1 所示。圖中， θ為無人艇的航向角，V為無人艇合速度矢量的模長，Vx和Vy分別為V沿x軸和y軸的速度分量。設定無人艇在t時刻的位置坐標為 (x(t),y(t))，狀態量為X(t)=[x(t)y(t) θ(t)V(t)]T， 控制量為u(t)=[γ(t)a(t)]T，則無人艇的動態方程（變量上方的符號“·”表示關于時間的一階導數）為

式中：V(t)為無人艇在t時刻的合速度矢量的模長；θ(t)為無人艇在t時刻的航向角； γ(t)為無人艇在t時 刻 θ 的 角 速 度；a(t) 為 無 人 艇 在t時 刻V的 加速度。

為便于描述，式（1）可以簡記為函數f：

圖1 無人艇運動學坐標系Fig. 1 Kinematic coordinate system of USV

1.2 靜態障礙物的規避區建模

在實際航行環境中，障礙物的形狀大多不規則，如果對障礙進行精確建模，勢必會顯著增加建模的復雜程度和工作量。為簡化處理，本文將采用圓形包絡面和凸四邊形包絡面來對障礙物進行包絡覆蓋。對于長寬比較小的不規則障礙物，可以采用圓形包絡面處理，如圖2（a）和圖2（b）所示。對于長寬比過大的細長型障礙物，如果仍然采用圓形包絡面處理，會造成較大的可通航區域浪費（圖2（c）），不利于航跡規劃。為此，對于細長型障礙物，宜采用凸四邊形包絡面進行處理，如圖2（d）所示。由障礙物包絡面和標準禁航區構成的不可航行區域，在下文統稱為禁航區（禁止無人艇航行的區域）。

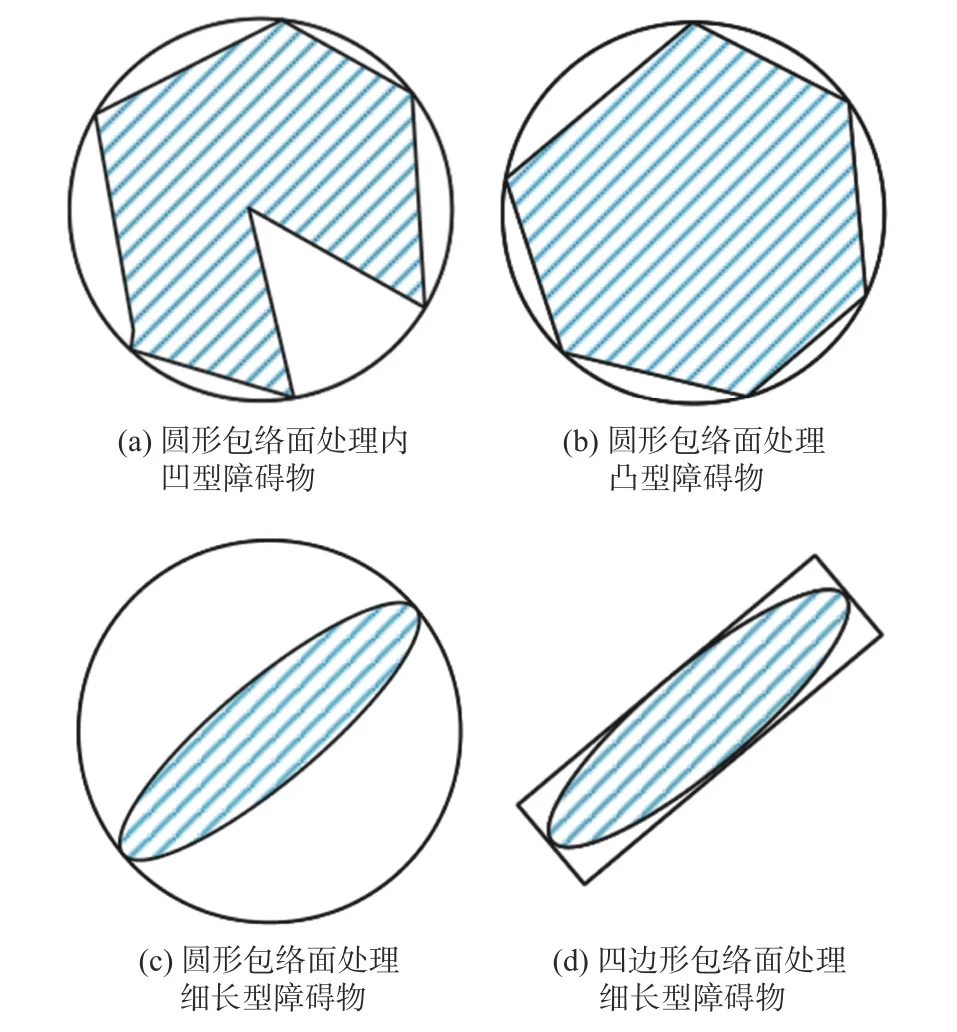
圖2 障礙物區域的包絡圖Fig. 2 Envelope diagram of obstacle area

1.2.1 圓形包絡面建模

對于長寬比較小的不規則障礙物，可以采用圓形包絡面以簡化建模的復雜度。將障礙物的最長端連線作為包絡圓的直徑，而直徑中點作為包絡圓的圓心，如圖3 所示，圓心記作 (xi,yi)，半徑記作ri，其中i為障礙物序號。為保證無人艇的安全性，需引入安全閾值 ρ，其值為船身長度的3 倍。將增加了安全閾值的包絡圓作為覆蓋障礙物的禁航區域，即圖3 中的虛線圓，其半徑Ri=ri+ρ。為使無人艇規避障礙物，則其位置應滿足：

1.2.2 凸四邊形包絡面建模

圖3 圓形包絡面建模Fig. 3 Circular envelope modeling

對于長寬比較大的不規則障礙物，如果繼續采用圓形包絡面進行建模處理，會浪費大量的可航行區域，增加無人艇的航行距離，甚至出現無可航行區域情況。為此，宜采用凸四邊形包絡面進行建模處理。如圖4 所示，凸四邊形包絡面由4 條相交的直線lj,1，lj,2，lj,3，lj,4（j為障礙物序號）圍合而成。圖4 中的實線凸四邊形為障礙物的最小面積包絡面，虛線凸四邊形為考慮了安全閾值 ρ之后的包絡面。本文將采用斜截式直線方程對lj,1，lj,2，lj,3，lj,4進行建模，設定kj,1，kj,2，kj,3，kj,4為4 條邊的斜率，bj,1，bj,2，bj,3，bj,4為4 條虛線邊對應直線在y軸上的截距。

圖4 凸四邊形包絡面建模Fig. 4 Convex quadrilateral envelope modeling

為使無人艇規避凸四邊形包絡面，其位置應滿足下列4 個不等式之一：

當某邊的斜率不存在時，所在邊的不等式約束形式即變為對x(t)的約束。為簡化約束形式，式（4）可以轉化為

式中： min(·)為取最小值函數；z=1，2，3，4，為凸四邊形包絡面的直線序號。

1.3 優化問題建模

航跡規劃的目標是：已知無人艇的初始狀態，在考慮禁航區域、最小/最大航行速度和終點位置約束的前提下，實現運動總時間的極小化，該問題模型（P1）為：

式中：C0 為控制量約束；C1 為無人艇運動學方程約束；C2 為無人艇的初始狀態；C3，C4 為終端位置約束；C5 為無人艇的航行速度約束；C6，C7 分別為圓形禁航區和凸四邊形禁航區；T為無人船的最大運動時間；γmax為最大轉向角速度；amax為最大航行加速度；X(0)為0 時刻的無人艇狀態；X0為無人艇的初始狀態；xT，yT為無人艇的終端位置坐標；Vmax是無人艇的最大航行速率；Ni，Nj分別為圓形包絡禁航區和凸四邊形包絡禁航區的障礙物最大數量。時間域 [0,T]是一個變化域，而約束C5～C7 中均包含每個時刻的狀態約束，這實際上將進一步產生無數個約束，所以給問題處理帶來了巨大的挑戰。

2 基于精確罰函數的最優控制算法

2.1 控制參數化

本文將采用時間尺度變換和控制參數化方法來處理上述優化問題。如圖5 所示，時間尺度變換將可變時間域t∈[0,T]變 換為固定域s∈[0, 1]，其中s為轉換后的時間刻度。由文獻[13-14]可知

圖5 時間尺度變換Fig. 5 Time scale transformation

為便于優化處理，本文將連續控制量在s∈[0, 1]內等分為K個區間，從而產生K+1 個節點{0,s1,s2,···,sK}，其中sK=1。分段參數化的結果如圖6 所示，其函數表達式為[15]

圖6 控制參數化Fig. 6 Control parameterization

因此，式（6）可以改寫為問題模型（P2）：

式中：S0～S7 為約束C0～C7 的改寫形式；x(1)，y(1)為s=1 時刻的位置狀態。

2.2 基于精確罰函數的約束處理

（P2）中含有終端等式約束S3 和S4 以及連續狀態不等式約束S5～S7，這就為問題求解帶來了極大的挑戰。為此，本文采用精確罰函數[13,16]來處理約束S3～S7，以便將（P2）轉化為僅含控制約束和初始狀態約束的優化問題，其優化目標函數J為：

以上式中： ?為懲罰參數；X(1)為無人艇的終端狀態； α ＞1, β ＞2, γ ＞2, δ,Wi,Wj均 為 正 實 數 參 數；??α為懲罰權重； δ?β為懲罰因子； ?γW為松弛因子，其中W為松弛因子的權重； κ為縮放因子。

對凸四邊形包絡面而言，當無人艇違反凸四邊形包絡面的約束時，必將同時違反凸四邊形包絡面4 條邊的約束，經過4 次累乘后，其懲罰值將遠大于違反圓形包絡面的懲罰值。因此，本文采用了縮放因子 κ來對凸四邊形包絡面約束進行縮放處理。

在優化初期，由于存在大量違反約束的情況，為了放寬對約束的懲罰程度，可以增加 ?以增加懲罰因子，從而減小懲罰權重并增加松弛因子；隨著優化的進行，違反約束的情況將逐漸減少，可以減小 ?來減小懲罰因子，從而增加懲罰權重并減小松弛因子，最終進一步減少違反約束的情況。當 ?趨近0 時，懲罰權重將趨于無窮大，松弛因子趨于0，懲罰因子趨于0，此時，即可認為優化結束后的目標函數J完全滿足了約束條件。

需注意的是， δ在理論上為正無窮才能使優化過程中的 ?趨近于0。在實際計算中， ?小于一定的閾值即可認為其足夠小，因此可將 δ設置為一個較大的常數值。對于松弛因子權重W，可以根據不同懲罰項的松弛程度來調整具體數值；關于其他參數的設置，僅需滿足理論要求的約束即可[16]。

式（12）是一個標準的最優參數選擇問題，為了將其轉化為常規的非線性優化問題，需獲得目標函數J的梯度方程[15]，即

基于式（17），即可將式（12）轉化為一個無狀態約束的最優參數選擇問題，且其適用于任何有效的分級優化器進行求解。

3 數值仿真

為了驗證本文算法的可行性，設定無人艇的初始狀態X(0)=[0, 0, 0.75, 5]T， 終點位置為(xT,yT)=(500, 500)， 最大速率Vmax=8 m/s；罰函數的相關參數為： α=1.5, β=3, γ=3, δ=108； κ=10?4；Wi=0.3，其中i=1，2，3，4，5，6；Wj=0.3，其中j=1，2，其他參數如表1 所示。

表1 仿真數據Table 1 Simulated data

為了驗證包絡面建模對禁航區域的普適性，本文在仿真中設置了不同半徑的圓形包絡面和凸四邊形包絡面，其Matlab 仿真結果如圖7 所示（藍色填充區域為實際禁航區，虛線包絡區為考慮安全閾值后的禁航區）。根據仿真結果，無人艇從初始位置出發，可以完全規避禁航區域，其理想航跡的總時長為100.6 s。從圖7 可以看出，為了極小化航行時間，航跡與1 個禁航區存在相切的情況，在實際航行過程中，某些不確定性因素的影響可能使無人艇存在碰撞危險。不過，本文設置了安全閾值，可以確保航行過程中無人艇與實際禁航區的安全距離。圖8 所示為無人艇位置隨時間的變化曲線。

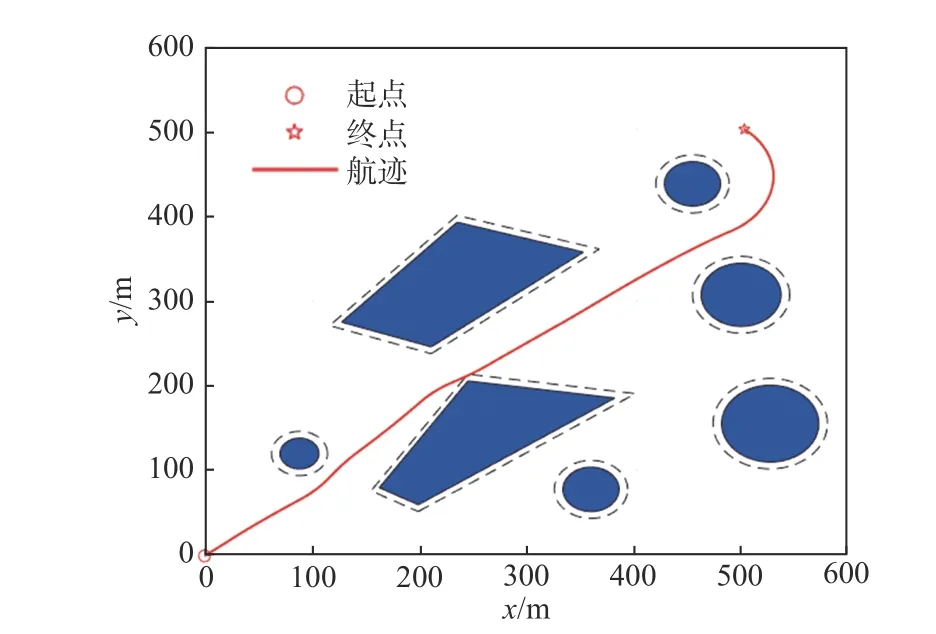
圖7 無人艇的航跡圖Fig. 7 Track map of USV

圖8 無人艇位置隨時間的變化圖Fig. 8 Diagram of USV position changing with time

圖9、圖10 所示為無人艇的運動速度和控制量隨時間的變化曲線，其仿真結果滿足相關約束條件。從圖9 可以看出，為了實現極小化的航行時間，無人艇在80 s 之前從初始狀態加速到了最大航行速度，并維持在最大速度附近；在80 s 之后，由于無人艇存在大角度的航向調整，為了極小化時間，需在轉彎半徑和轉彎速度之間進行權衡，雖然較小的轉彎半徑可以縮短轉彎航程，但需同時減小航行速度。從仿真結果可以看出，為了極小化航行時間，該無人艇的航向角速度正向滿舵且航行速度下降，從而匹配了最佳的轉彎半徑。可見，該仿真結果驗證了本文算法的有效性。

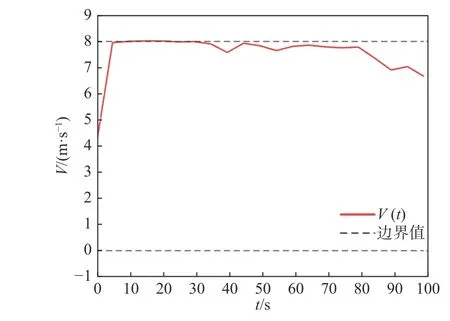
圖9 無人艇速度隨時間的變化曲線Fig. 9 Diagram of USV speed changing with time

圖10 輸入控制信號Fig. 10 Input control signal

4 結 語

本文采用圓形和凸四邊形包絡面處理不規則障礙物，將規避不規則障礙物的問題轉化為笛卡爾坐標系下的不等式約束條件，從而將無人艇避障航跡規劃問題構建為含有連續狀態不等式約束和終端約束的時間最優控制問題。通過控制參數化和時間尺度變換，將時間最優控制問題進一步轉化為了最優參數選擇問題；同時，利用精確罰函數方法，將連續狀態不等式約束和終端約束構建為約束懲罰函數并添加到目標函數中，最終轉化為一個無狀態約束的最優參數選擇問題，其適用于任何有效的分級優化技術進行求解。因此，本文所提出的算法可以有效處理無人艇航跡規劃中的避障問題。