基于傳感器陣列多目標優化的SP-QPSO算法研究

孔宇航，陶 洋，梁志芳

(重慶郵電大學通信與信息工程學院，重慶 400065)

0 引言

電子鼻系統又稱仿生嗅覺系統，通過模仿生物嗅覺系統的工作原理從而檢測目標氣體[1]。當有氣體經過電子鼻系統時，其中傳感器陣列中的某些傳感器會產生物理變化，傳感器檢測到這種物理變化后將其轉換為電信號，從而產生特定的特征或者氣體印記。經過一系列數據處理后，應用現有的智能模式識別方法實現氣體的識別[2]。其中，對廣譜化合物產生響應的傳感器陣列是關鍵組成部分，傳感器陣列的響應直接決定了模式識別系統的輸入質量。在檢測待測氣體前，由于不清楚哪些傳感器對識別結果影響較小，所以初始陣列中會盡可能選取不同特性的傳感器。這會造成某些傳感器的廣譜響應特性產生冗余信息[3]。其次，傳感器數量過多將導致后續數據處理爆發“維數災難”[4]。如何選取對最終識別氣體有最大幫助的傳感器組合，即經過傳感器陣列優化后，將有效地提高電子鼻系統檢測結果的識別精度，同時滿足電子鼻系統的微型化和智能化的需要。

近年來電子鼻陣列優化的研究方法不斷涌現。針對醫療傷口檢測中等待時間長、操作過程繁瑣等問題，Yan Jia提出了一種結合支持向量機的粒子群優化算法[5]，該方法大大提高了傷口感染細菌的分類準確度，最終實現傳感器陣列和分類器參數的同步優化。Sun Hao通過搭建30個氣體傳感器構造一個電子鼻系統同樣用于傷口細菌檢測中常見的金葡萄球菌、大腸桿菌和銅綠假單胞菌[6]，采用wilks統計的方法，分別使用直接選擇法和逐步選擇的思想選擇或剔除無用傳感器，在保證識別精度同時，有效地減小了傳感器陣列的規模。Chang Meizhuo等人利用15個氣體金屬氧化物傳感器檢測不同品種的茶香[7]，使用基于聚類分析及區分性能值的氣敏傳感器陣列篩選方法，通過聚類分析驗證各傳感器的獨立性，選取區分性能值較大對應的傳感器，最終得到最優的傳感器陣列保證了整個電子鼻系統的輸入質量，有效地識別出6個不同品種的龍井茶。

本文首先通過聚類分析預估傳感器陣列的大小。再將傳感器靈敏度的特性即選擇性和多樣性作為傳感器信息度量的標準，構造兩個目標函數。改組復合體演化算法用于構建復合體并監測種群維數的變化。量子行為粒子群優化算法用于每個復合體在搜索空間中的演化。其中，采用自適應的懲罰函數處理約束優化問題將更易于求解。最后，通過支持向量機對優化后的傳感器子集進行分類和驗證。

1 基于改組復合體演化量子行為粒子群優化算法相關原理

1.1 多目標優化函數構造

一般情況下，選擇靈敏度高的傳感器可以提供關于每種氣體所包含的最多的相關信息。但傳感器相互之間往往存在交叉敏感特性，即它們的敏感氣體之間不可避免地存在著交叉和重疊，很容易產生冗余信息。另外，對于每種氣體，其響應模式由陣列內所有傳感器的靈敏度決定，傳感器靈敏度的差異性越高，其模式區分越明顯。所以同時也將傳感器靈敏度的差異性作為影響陣列優化的因素之一。

假如存在區分N類待測氣體的分類任務，初始陣列中傳感器數量為M，優化后的傳感器數量為K（K≤M ），把全部的傳感器靈敏度Sij構成一個初始矩陣[8]。構造兩個關于傳感器特性的目標函數。目標函數1是由靈敏度矩陣中列的信息熵組成，對于傳感器 j，其選擇性越高，靈敏度矩陣第j列的熵值就越小。目標函數 2是由靈敏度矩陣中行的信息熵組成，對于氣體i，其差異性越大，靈敏度矩陣第i列的熵值就越小。

以傳感器選擇性構造目標函數1：

（1）計算第 j列中元素的總和，并對Sij歸一化處理：

其中i和 j分別表示氣體類別和傳感器，j的值在優化過程中動態確定。

（2）計算每個選定傳感器j的信息熵：

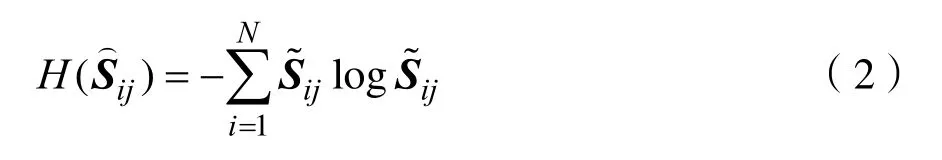
（3）獲取N類氣體分析物獲得的最大信息熵：

（4）K個基于信息熵的傳感器選擇性的目標函數1：

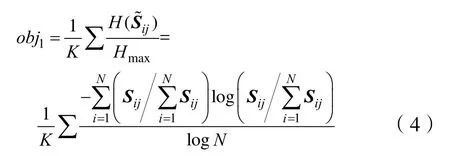
同理，N個基于信息熵的傳感器差異性的目標函數2：

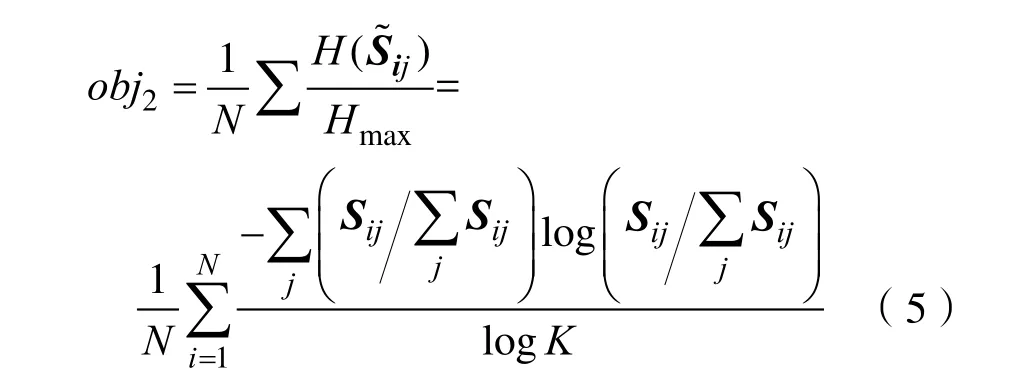
以上兩個目標函數的值都在[0,1]范圍內，最小化這兩個目標函數將分別獲得傳感器最大的選擇性和多樣性。在多目標優化過程中使用這兩個目標函數，所得的傳感器陣列將得到最相關的信息。

1.2 約束優化

在求解多目標優化問題時通常涉及約束優化的情況，所以如何平衡約束優化和目標函數是一個重要的難題[9]。在目標函數中加入懲罰項，該函數一般由懲罰參數乘以違反約束的度量組成，進而使約束優化問題轉化為無約束優化問題[10]。

給定n維解X，其中 X = (x1, x2,… ,xm)，將M個目標的約束優化問題定義為：

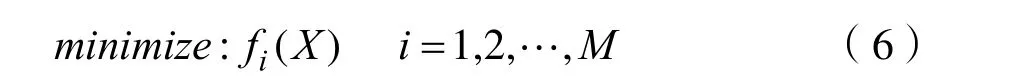
常見的懲罰函數模型是由目標函數與懲罰項之和組成，二者共同構成了適應度函數。其中X到可行域距離稱為違反度，其違反度函數表示為：

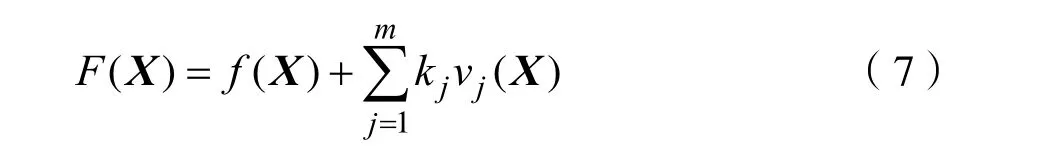
其中F(X)是適應度函數，f(X)是目標函數，j是約束條件個數， j = 1 ,2,… ,J 。kj是個體在約束 j上的懲罰系數，vj(X )是個體在約束 j上的違反度。

對公式（7）中懲罰項的參數進行改進，采用一種自適應懲罰函數，即在優化過程中動態調整懲罰系數：

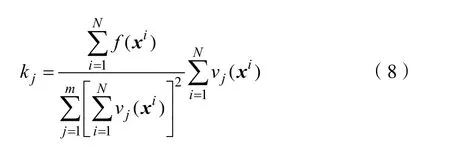
其中 f( xi)代表當前種群中目標函數的平均值， vj(xi)表示當前種群中 j個平均約束違反度的大小，N是種群大小。

結合構造的目標函數公式（4）和（5），則整個種群的適應度函數為：

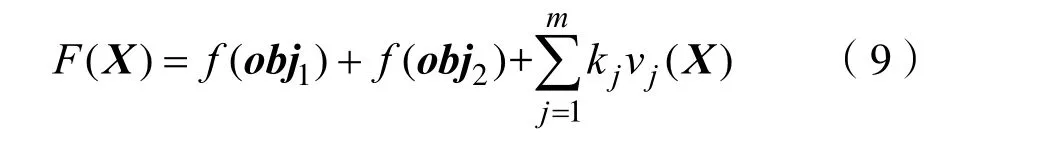
在計算出每個解的約束違反程度和適應度值之后，根據約束支配規則，在任意兩個候選解之間選擇非支配解。

1.3 改組復合體演化算法

在高維空間中可能存在某些問題，例如“維數災難”，這嚴重影響了高維空間算法的執行效率。最早解決高維空間問題的單純形作為一種局部搜索算法[11]，但是粒子可能會收斂到原始搜索空間的一個子空間，后續的演化將被限制在子空間內，并且幾乎無法恢復到原參數空間中的完全搜索，這種現象稱為“種群退化”。有研究學者提出了主成分分析的改組復合體演化算法（Shuffled complex evolution with PCA with University of California, Irvine, SP-UCI）用于解決上述“種群退化”問題[12]。它的原理是如果算法通過數據集丟失了n個維度，則最后有n個主成分上的數據投影方差等于零。通過沿主成分以零方差添加新的數據點來幫助恢復丟失的維數。SP-UCI算法中的點在搜索空間中呈隨機分布，所有的點存儲在數組 D = { xi,fi, i = 1 ,2,… ,s}，其中 fi是xi對應的函數值。經過初始化后，將種群數組D劃分m個復合體 A1, A2, …,Am，每個復合體包含p個點。復合體的具體表現形式為：

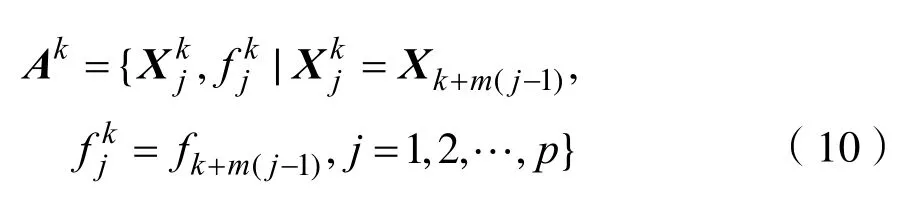
在每次迭代中，將復合體采用改組的方案，即把復合體之間以一種共享獲得信息的方式來構造新的復合體。在每個階段中，存儲在數組中的復合體都要排序和替代。經過改組和構造的新復合體會不斷地再生，直至滿足最終的條件。

利用 SP-UCI策略有助于算法檢查和監控維數的變化，避免“種群退化”，并確保在優化過程的開始就訪問搜索空間中的所有區域。

1.4 量子行為粒子群優化算法

量子行為粒子群優化（Quantum behaved Particle Swarm Optimization，QPSO）是一種量子模型概率化粒子群優化算法[13]。它的原理是將粒子的尋優過程看作勢場中粒子向勢能最低點移動的過程。QPSO算法不僅提高了原始PSO算法的全局收斂能力，而且更易于算法的實現和參數的選擇。該算法的計算公式為：

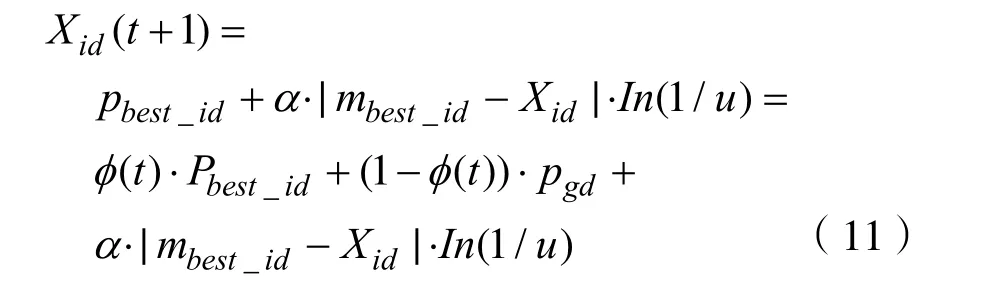
其中α作為收縮-膨脹系數用來控制算法的收斂速度， α = 0 .5 + 0 .5(T - t )/T ，T是總迭代次數，t是當前迭代次數。

1.5 列文伯格馬夸爾特算法

列文伯格-馬夸爾特算法（Levenberg-Marquardt，LM）是眾多最優化算法中比較有效的一種方法[14]。它的原理是假設初始數據點附近存在可以信賴的最大位移s，以s為半徑所劃分的區域內，尋找目標函數的一個近似最優點，從而求解得到發生的位移。計算目標函數值后，假如其下降的范圍達到了一定條件，則繼續按照該規則迭代求解下去；如果沒有達到這一條件，則相應的減小一定位移的范圍，然后重新計算求解。LM 優化算法有助于SP-QPSO算法加快收斂速度，保證所有粒子向最優解的方向移動。

基本的LM優化算法的定義為：

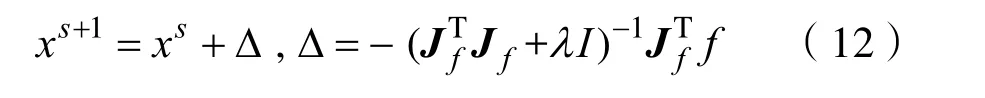
2 基于改組復合體演化量子行為粒子群優化算法

為了提高算法在高維空間優化問題的性能，提出了一種 SP-UCI算法和 QPSO算法混合的算法SP-QPSO，即基于改組復合體演化量子行為粒子群優化算法（Shuffled complex evolution with PCA-Quantum behaved particle swarm optimization,SP-QPSO）的傳感器陣列多目標優化研究方法。使用 1.1章節中構造的兩個關于傳感器特性的目標函數，以求函數最優值為優化目標。下面詳細介紹提出的SP-QPSO算法，算法的全流程步驟如算法1所示。

算法1SP-QPSO算法的全流程步驟

基于改組復合體演化量子行為粒子群優化算法

輸入：初始化種群大小，最大迭代次數等參數；

輸出：非支配Pareto解集；

過程：

Step.1初始化m個復合體，每個復合體中包含p個點，采樣大小為s=m*p，樣本的維數d，搜索空間為 X1, X2,… ,Xs。

Step.2在搜索空間中初始化種群的大小。計算每個點的函數值，根據函數值對這些點進行排序，并存儲在數組 D = { Xi,fi, i = 1 ,2,… ,s}。

Step.3對高維空間中的特征進行維數檢查。如果存在“種群退化”現象，檢查出丟失的維度并恢復。

Step.4將數組D劃分為m個復合體，Ak=

Step.5使用QPSO分別進化每個復合體kA，每個復合體尋找其最優函數值。

（1）初始化種群大小N和最大迭代次數T。

（2）在復合體 Ak中建立一個包含N個點的子集群計算其函數值，并將其存儲在，其中 Yik是粒子，vik表示函數值。

（3）通過比較搜索空間中所有局部最優位置找到最優值，并將其分配給全局最優值。

（4）為下一次迭代計算種群的平均最優位置mbest以及粒子向全局最優值移動的位置。

（5）重復上述過程，直到滿足最大迭代次數或者停止標準為止。

Step.6多正態重采樣檢驗陷入局部最小值的概率。

Step.7復合體重新改組，將 A1, A2,… ,Am替換成一個數組并對其進行排序。

Step.8重復上述過程，直到滿足停止標準為止。

Step.9群體最優位置轉化為對應Pareto最優子集。

3 實驗驗證與分析

3.1 數據集介紹

本文中，數據集來自加州大學圣地亞哥分校實驗室[15]，由8個MOX金屬氣體傳感器組成的氣體傳感器陣列采集。傳感器的型號類型詳細信息如下：R1:TGS2611 R2:TGS2612 R3:TGS2610 R4:TGS2600 R5:TGS2602 R6:TGS2602 R7:TGS2620 R8:TGS2620。數據集由100個時間序列的片段組成，每個片段都是一次歸納或背景活動，總計919438點。該傳感器陣列長期放置于家庭中，數據集包含3種共100個不同條件的時間序列：葡萄酒、香蕉和背景活動。其中包括葡萄酒的36種響應記錄，香蕉的 33種響應記錄，背景活動的31種響應記錄。

3.2 實驗設置

本文的實驗環境為MATLAB R2016a。提出的SP-QPSO算法中，初始粒子種群設置為20，最大迭代次數為1000，粒子維度為30，在搜索空間中隨機初始化粒子位置。所選的分類器是基于徑向基函數的SVM，核參數和懲罰因子均采用默認值。

3.3 實驗結果分析

傳感器陣列中某些響應之間存在相關性，這些傳感器提供的信息之間可能存在冗余。首先通過聚類分析中的離差平方和方法分析該數據集的相關性，通過歐式距離評估傳感器大致可分為幾類，分析潛在的傳感器最優組合的數量，從而為確定最終陣列中傳感器的數量提供參考依據。SPSS Statistics 20軟件對該過程進行分析，所得的結果用樹狀圖表示，如圖1所示。

由圖1可知，該數據集涉及的這8個氣體傳感器大致分為4組：A組（傳感器S1和S3），B組（傳感器S2），C組（傳感器S4、S7、S8），D組（傳感器 S5、S6）。每組類別中傳感器的信息非常相似。這說明了某些傳感器的響應之間的確存在共線性。因此，最優傳感器陣列可能需要 4個左右的傳感器數量以區分目標氣體。

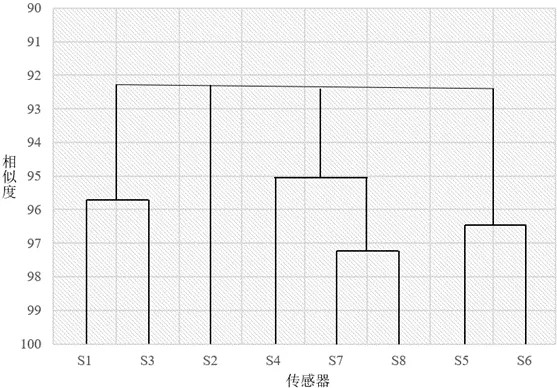
圖1 數據集通過聚類分析得到的樹狀圖Fig.1 dendrogram obtained by cluster analysis of the data set

然后利用提出的 SP-QPSO算法通過數據集驗證，運行10次后的結果如表2所示。表中信息包括Pareto解集的數量、運行10次時間的平均值、運行成功次數。結果表明傳感器陣列大小為3、4、5、6時，均存在Pareto最優解集，其余情況下不存在 Pareto解集。當傳感器陣列大小為 5時，Pareto解集的數量有最多的13個，此時的平均運行時間最長。同時由于該算法存在不穩定的因素，在約束優化中加入懲罰函數后，實際僅出現了 2次運行失敗的情況。并且Pareto解集大部分集中在傳感器陣列大小為4個左右，有效地驗證了采用聚類分析對數據集的初步分析。

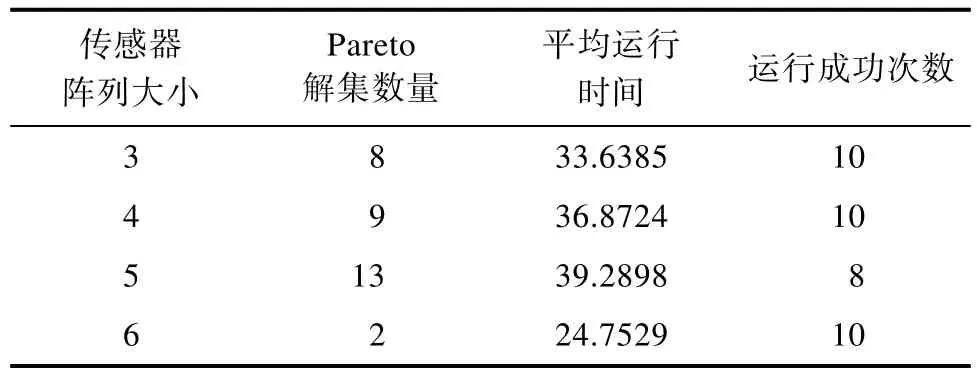
表2 SP-QPSO 算法運行實驗結果Tab.2 the running experiment results of SP-QPSO algorithm

利用傳感器靈敏度的選擇性和差異性這兩個特性，構造了兩個目標函數，其傳感器陣列大小為3、4、5、6時的Pareto解集分布如圖2所示。可以看到圖中Pareto集合中非支配解的數量并不總是隨著最佳陣列大小而增加。Pareto優化解的個數隨著陣列大小先增加后減小，傳感器陣列大小為3時存在8個Pareto解集，傳感器陣列大小為4時存在9個Pareto解集。當陣列中傳感器個數為5時，存在13個最多的Pareto解集。而當陣列中傳感器數目為6時，僅存在2個Pareto解集。因此Pareto解集主要取決于解決方案的分布，而不是優化陣列大小。

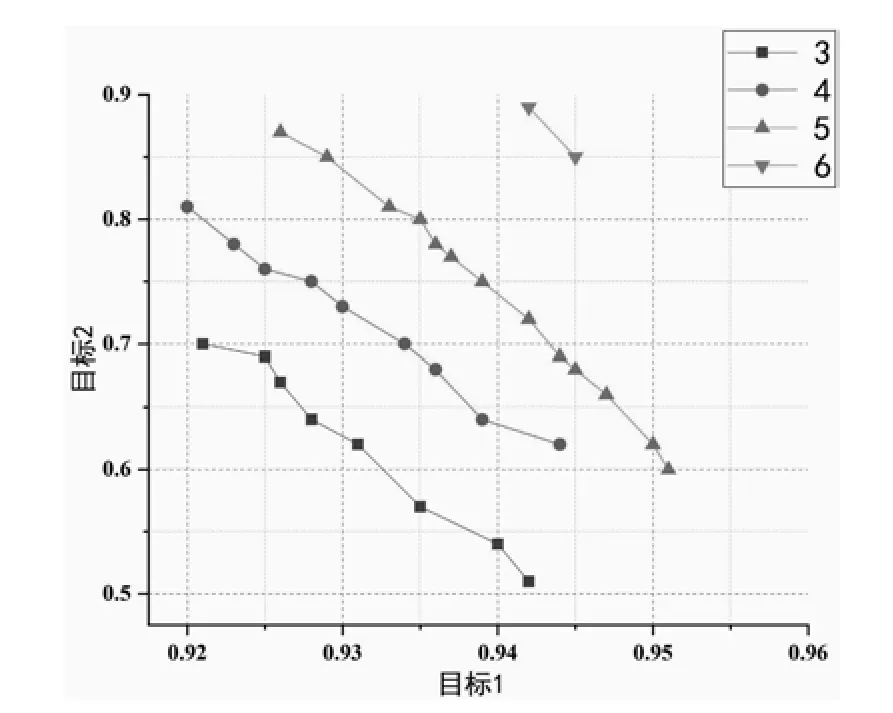
圖2 優化后不同陣列大小下Pareto優化解的個數Fig.2 the number of pareto optimization solutions under different array sizes after optimization

為了準確地驗證本章提出的基于 SP-QPSO算法用于電子鼻傳感器陣列多目標優化。在單目標優化和多目標優化兩種場景下，將粒子群優化算法（PSO）、帶權重的粒子群優化算法（SPSO）、量子行為粒子群優化算法（QPSO）作為對比算法，隨機選取各自優化后的10組Pareto解集，其中單目標優化僅使用傳感器選擇性的特性構造的目標函數1，然后采用支持向量機SVM對數據集中3類目標氣體的響應值進行分類，觀察分類結果。各算法的分類精度如表3所示。

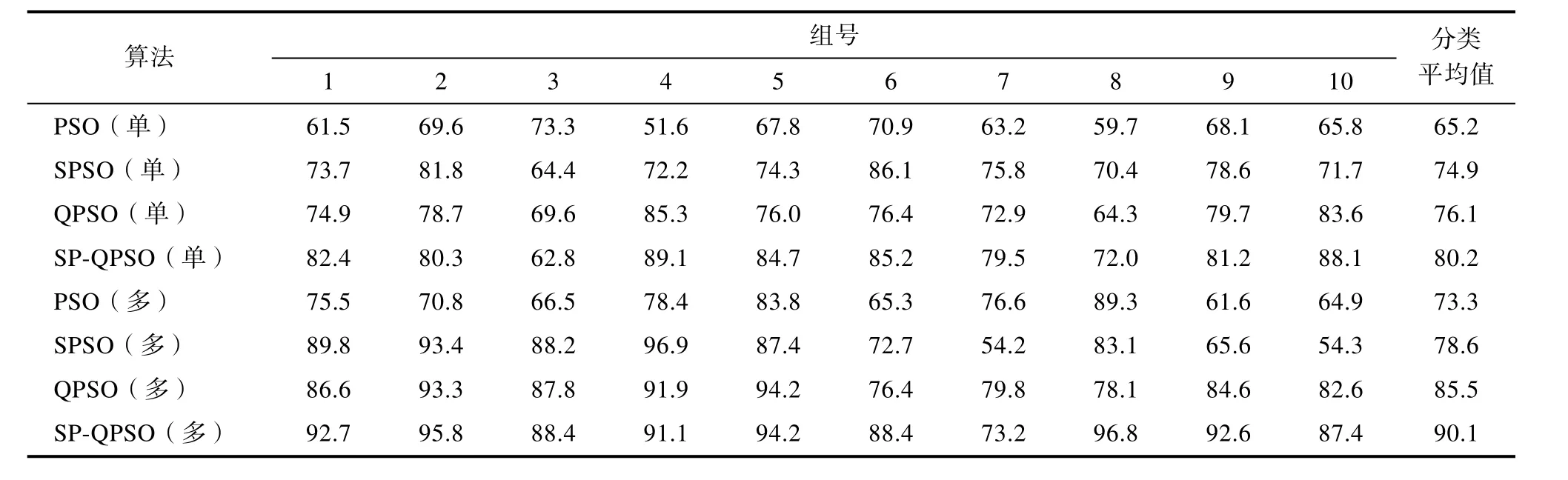
表3 不同算法場景下單目標和多目標優化后的結果(%)Tab.3 results of single objective and multi-objective optimization in different algorithm scenarios (%)

可以看到在單目標優化場景下，SP-QPSO算法的平均分類精度最高，達到了 80.2%。該算法在10組的Pareto優化解中，有6組取得了更好的分類精度。同樣在多目標優化場景下，SP-QPSO算法在全部的對比算法中平均精度最優，達到了90.1%，有 7組 Pareto解對應的傳感器組合取得了更優的分類精度。即該算法驗證了在高維樣本空間中處理約束優化問題的優勢。為了更直觀地反映各算法在陣列優化的分類能力，不同算法下在單目標和多目標場景優化后的對比圖如圖3所示。此外，這些算法的分類精度均高于初始陣列傳感器組合的分類精度，充分證明了本次陣列優化的有效性。而且不論何種算法，多目標優化場景下算法取得的分類精度明顯優于同類算法單目標優化場景下的分類精度，即多目標優化保證了電子鼻傳感器陣列擁有更好的輸出質量。

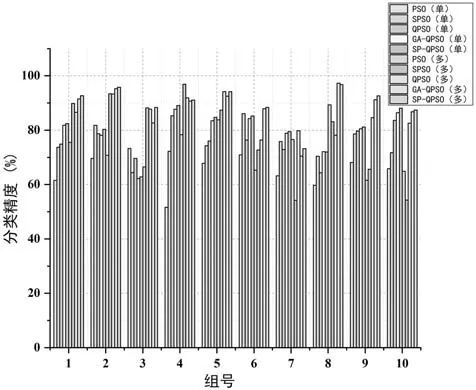
圖3 不同算法下單目標和多目標優化后的對比圖Fig.3 comparison of single objective and multiobjective optimization with different algorithms

4 結論

在高維空間中，傳感器陣列優化過程在一定程度上為后續的數據處理帶來“維度災難”，同時可能存在“種群退化”的現象。提出了一種基于改組復合體演化量子行為粒子群優化算法（SPQPSO）的傳感器陣列多目標優化研究方法。該方法具有以下特點：（1）SP-UCI算法用于構建復合體并監測種群維數的變化，QPSO算法用于每個復合體在搜索空間的演化。（2）引入自適應懲罰函數計算搜索空間的違反度，以指導搜索空間可行區域的求解。實驗仿真結果表明，SP-QPSO算法在多目標優化場景下算法具有更好的分類精度，這對傳感器陣列優化過程中高維空間產生的數據處理后的效果更好。這充分驗證了基于SP-QPSO算法地傳感器陣列多目標優化研究的有效性，最終用較少數量的傳感器構建了高質量的陣列。