基于偏微分方程的定向插值在偏移成像中的應用

韓復興， 孫章慶， 陳祥忠， 高正輝， 王瑞興， 劉俊成， 王麗麗

1 吉林大學地球探測科學與技術學院， 長春 1300262 北京桔燈地球物理勘探股份有限公司， 北京 1022003 吉林油田地球物理勘探研究院， 松原 138006

0 引言

基于彈性波傳播方程高頻近似的射線理論類偏移成像技術(Hill, 1990, 2001; 高成等, 2015; Gao et al., 2017；韓建光等，2017)，其在實現偏移成像的過程當中，采用射線理論方法求解運動學和動力學射線追蹤系統獲得波場傳播所需的走時振幅和相位信息，然后進行地震波場的延拓外推從而達到最終成像的目的.其實現過程和實現方式相對于波動方程類偏移成像具有很大的時效性和經濟性，因此一直是工業界應用的主流成像方法和技術(岳玉波, 2011；楊珊珊等，2015；袁茂林等，2016).基于體波、面波等地震彈性波和電磁波的有效聯合，解譯了華南深部結構(Di et al., 2021).那么在應用射線理論實現波場延拓成像的過程當中，難免會遇到依賴速度模型進行的射線追蹤系統的求解.在實際應用過程當中，一般給定的速度模型都比較復雜，而且是以離散的形式只給定網格節點上的數值，非網格節點上的值只能通過構建的插值算法來進行插值計算.在應用射線理論進行運動學和動力學追蹤計算中，波場隨著時間的不斷外推增加，每一步計算所應用到的速度場信息不一定都落在給定的原離散網格上，如果計算所需要的速度場不在給定的離散節點之上，就需要對速度模型進行插值計算，從而解決在波前外推當中速度在x、z方向上非網格節點處的插值問題.眾所周知，插值算法以及應用插值算法所得的插值計算結果的準確性直接影響著速度模型上計算的走時、相位和振幅，最終影響到偏移成像的質量(韓復興, 2009).在偏移成像的過程當中，給定的速度模型往往都具有一定的速度梯度，如何根據速度梯度的空間變化選擇一種高效、穩定的插值算法對于實現基于高頻近似理論的射線類偏移成像有著十分重要的作用(Gao et al., 2017).

截止到目前為止，在數值計算當中常用的插值算法主要分為兩大類型：第一大類型主要為通過給定的網格節點上的數值直接進行插值計算，例如雙線性插值、分片線性插值、臨近域插值、距離加權插值等.直接計算這種類型的插值算法經過幾十年的發展和完善，算法相對成熟和穩定，而且簡單實用、計算速度快.在實際插值計算處理當中，該類插值算法只需要4個已知網格節點上的屬性值進行插值計算，但缺點在于只能達到二階近似的計算精度，確保了計算的效率而忽略了計算的精度問題；第二大類型主要為基于構建插值核函數的插值計算方法，例如卷積類插值(韓復興等, 2008a，b)、樣條插值、雙立方厄米特插值(王德人和楊忠華, 1990; Keys, 1981)、雙三次多項式插值等等，該類插值算法依據所構建的核函數不同，所選取插值點周圍的網格節點數也不盡相同，二維三次卷積、雙三次多項式插值等需要插值點周圍的16個網格節點上的屬性值進行插值，二維四次卷積依據其核函數需要插值點周圍的36個網格節點上的屬性值進行插值.由于采用的網格節點數比較多，該類核函數插值算法計算精確度相對比較高，并且根據實際需求可以滿足插值結果在網格點處的一階導數、二階導數連續，在實現的過程當中考慮算法的優化能夠同時保證計算具有較高的計算效率.但該類算法存在的問題在于由于插值過程當中應用的插值點周圍的網格節點數較多，雖然保證了插值結果的計算精度和導數的連續性，但對于速度梯度在空間上變化劇烈的模型來說，忽略了原始速度模型橫向、縱向空間結構的變化，從而造成插值結果后的速度模型不滿足原始速度模型空間梯度的連續性.也就是說基于插值核函數的插值算法的缺點在于其插值函數一旦固定下來對于整個模型空間來說就是不變的，這種不變性對于速度梯度變化不明顯的模型來說是可以適應的，但對于速度梯度在橫向和縱向變化較大的模型來說，這個固定核函數的插值算法就很難適應.如果應用基于固定核函數的插值算法在速度梯度變化劇烈的模型上進行插值計算就會造成梯度變化大的地方邊緣模糊和鋸齒現象，最終造成射線路徑、走時和振幅相位的誤差，影響偏移成像的結果.

為了解決上述射線類偏移成像求解射線追蹤系統當中遇到的速度在波場延拓過程當中的不連續問題，本研究的主要內容就是考慮原始速度模型的空間結構，基于變分原理引入基于速度梯度構建的偏微分方程插值算法，使模型空間被插值點處速度梯度的空間變化盡可能與原始模型保持一致(Perona and Malik, 1990; Catté et al., 1992; Alvarez et al., 1992; Jiang and Moloney, 2002a,b)，從而實現基于原始速度模型空間梯度變化的插值計算.由于偏微分方程方法本身所固有的特性(局部特征不變性、解的唯一性和線性疊加性)，自偏微分方程算法提出以來，隨著時間的推移，目前已經應用到各個領域(Perona and Malik, 1990; Catté et al., 1992; Alvarez et al., 1992; 仵冀穎, 2009; 肖義男, 2005).因此，在射線類偏移成像當中應用基于速度梯度構建的偏微分方程插值算法可以最終實現不破壞原始速度模型空間結構前提下的插值計算，從而獲得較為準確的走時、振幅和相位信息，最終提高偏移成像的質量.

1 偏微分方程(Partial Differential Equation)的插值算法

基于速度梯度構建的偏微分方程插值算法在進行插值計算的過程當中引入總變分最小原則，使被插值點的速度值v(x,z)滿足(Jiang and Moloney, 2002a,b)：

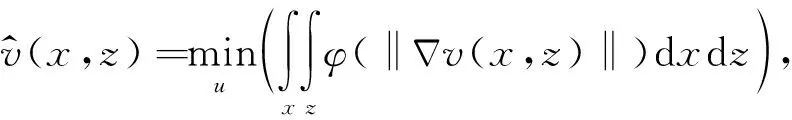
(1)

也就是要求需要插值地方的速度的梯度盡可能與原始速度模型的空間結構保持一致，從而達到對原始速度模型空間結構的保護性.其約束條件為采用基于速度梯度構建的偏微分方程在網格節點上所得的插值計算結果必須等于原始速度模型網格節點上的速度值，即：

(2)

其中v(i,j)是原始速度模型空間網格節點上的速度值，X和Z是原始速度模兩個方向上的空間尺度，Δh、Δk是X方向和Z方向上的空間采樣間隔，φ(·)≥0是一個遞減函數.

對于公式(1)來說，初始條件的選擇直接決定著該問題的求解難易程度.為了使公式(1)的求解簡單化，引入對被插值點速度方向角的條件限制(Jiang and Moloney, 2002a,b)：

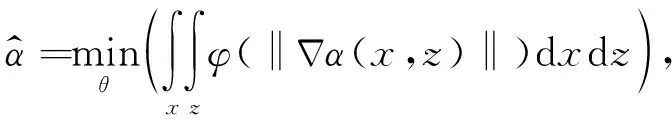
(3)

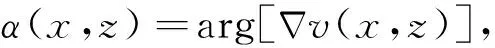
假設已知原始速度模型網格節點處的梯度角，且在應用基于速度梯度構建的偏微分方程插值計算過程當中原已知的梯度角不隨插值條件發生改變，即限定條件為：

(4)

(5)

在實際插值計算當中梯度角α(x,z)可以采用數值計算的方法獲得.

基于以上假設，在偏微分方程插值計算的過程當中，首先需要求解梯度角α(x,z)，即(3)式，接下來求解基于約束條件(2)和約束條件(4)的變分問題，即可解決基于變分原理的插值計算問題.

關于插值點處梯度角的計算問題如下，對應(5)式的Euler方程為：

(6)

由于在實際計算過程當中只使用插值點4個斜線方向上的相鄰速度值，所以(6)式可以簡化為：

(7)

其中k∈{(i,j),(i,j+1),(i+1,j),(i+1,j+1)}，αk表示對應于第k個速度點上的梯度角，因此得到非線性方程(7)的解為：

(8)

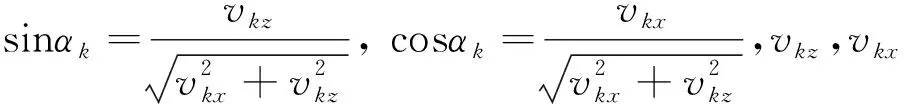
(9)

將公式(9)展開并代入方向角限定條件化簡得到：

(10)

公式(10)是關于插值點處的梯度角以及插值點處速度偏導數的計算公式，將該公式采用數值計算的方法進行離散處理，然后應用被插值點周圍的4個已知點上的速度值就可以進行插值計算求得被插值點處的速度值.其具體的計算步驟如圖1所示.

圖1中G(x,z)為需要插值的點，h為速度模型X方向上的網格間距，k為速度模型Z方向上的網格間距，v(i,j)、v(i+1,j)、v(i,j+1)、v(i+1,j+1)為已知網格節點上的速度值，A1、A2、B1、B2為計算過程當中的待求點，偏微分方程插值計算步驟如下：

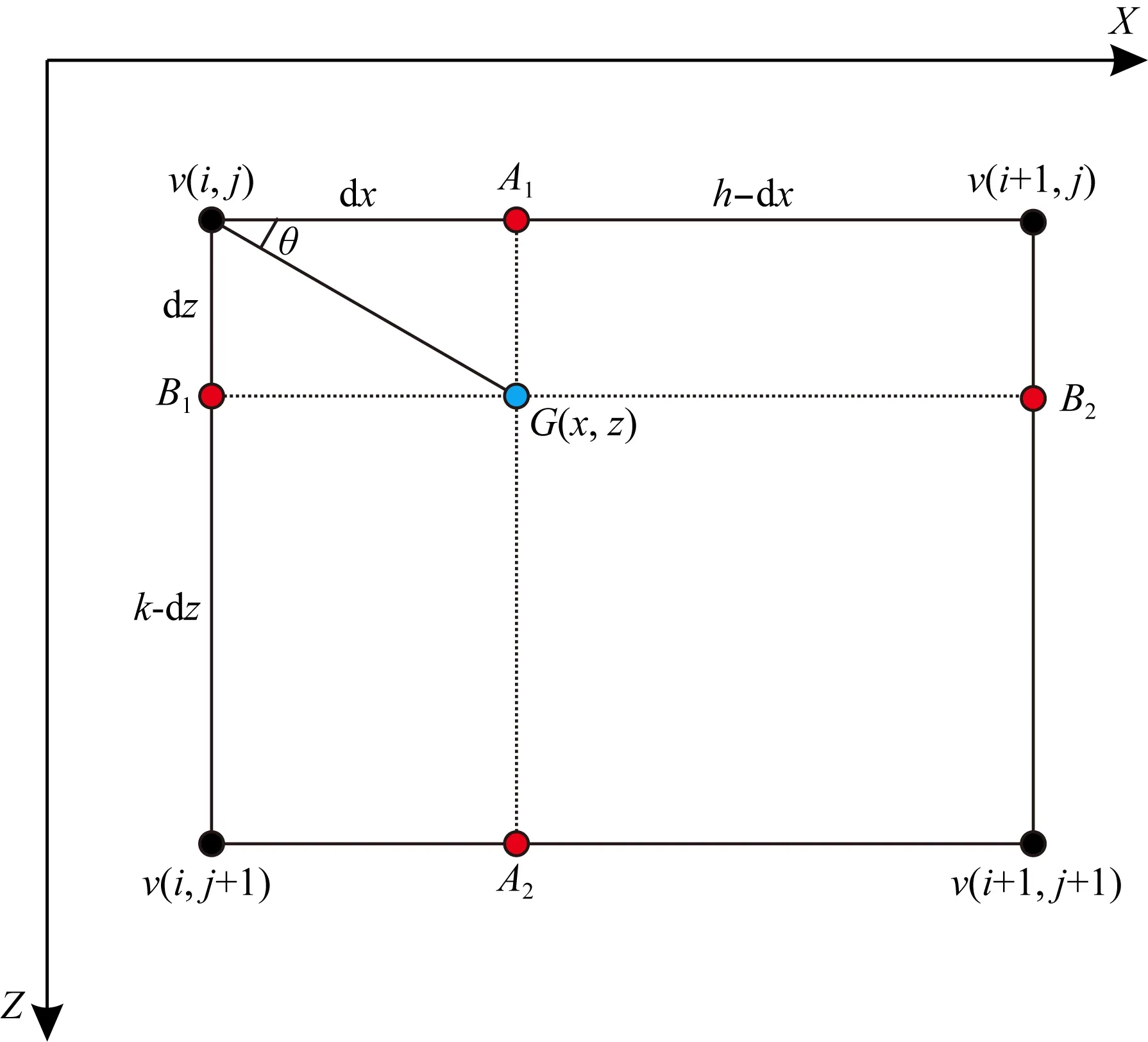
圖1 基于速度梯度的偏微分方程插值示意圖Fig.1 Schematic diagram of partial differential equations interpolation

(1)首先應用四個已知網格節點上的速度值v(i,j)、v(i+1,j)、v(i,j+1)、v(i+1,j+1)求解待定點A1、A2、B1、B2，即：

(11)

(2)然后應用不等距差分和泰勒級數展公式求解被插值點處的速度導數值vxx(x,z)、vxz(x,z)、vzz(x,z)，即：

(12)

(3)把通過第二步解出的值vxx(x,z)、vxz(x,z)、vzz(x,z)、vzx(x,z)帶入公式(10)，就可以獲得待求點處的速度值G(x,z)，其公式為：

(13)

其中：

(14)

2 插值試算

下面以地震數據處理當中常用的Marmousi速度模型和Sigsbee速度模型為例，分析說明在原始速度模型上進行插值計算后速度模型空間結構特別是模型邊緣位置的變化情況.Marmousi速度模型橫向384個網格節點，縱向122個網格節點，原模型橫向和縱向的網格間距Δx=Δz=24 m，現在采用dΔx=dΔz=4 m的間距進行插值計算，插值后速度模型橫向網格點數為2298，縱向網格點數為726，在相同的運算環境下，采用卷積類插值算法插值計算耗時18.899 s，采用偏微分方程插值計算耗時16.204 s，原Marmousi模型和經過卷積插值、PDE插值計算后的結果如圖2所示.為了進一步分析說明不同插值算法對速度模型空間結構和速度梯度變化區域邊緣的影響，將原模型和插值計算后模型紅色局部區域進行放大，如圖3所示.通過圖3可以看出，采用固定核函數的卷積類插值算法在原始速度模型空間結構梯度變化劇烈的區域，由于采用的插值點數較多(16個)，插值造成的結果就是破壞了原模型的空間梯度結構，因此造成插值后速度模型紅色部分同原始速度相比，在邊緣區域變得模糊，而基于速度梯度構建的偏微分方程插值算法，由于去插值函數的單調性和可變性，插值結果基本保持和原始速度模型空間結構的一致性.

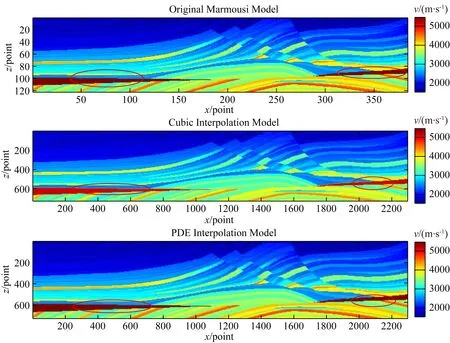
圖2 Marmousi速度模型以及應用不同插值算法插值后的速度模型Fig.2 Original Marmousi velocity model and its interpolation results using cubic and PDE algorithms

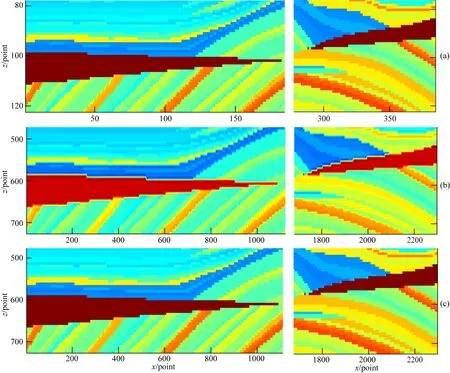
圖3 (a) 原速度模型局部區域放大； (b) 卷積插值后局部區域放大； (c) 偏微分方程插值后區域局部放大Fig.3 (a) Partially enlarged area of original Marmousi model; (b) Partially enlarged red area of interpolated Marmousi model used cubic; (c) Partially enlarged red area of interpolated Marmousi model used PDE

Sigsbee速度模型橫向2400個網格節點，縱向800個網格節點，橫向網格間距Δx=37.5 m，縱向網格間距為Δz=25 m.采用x方向間距為dΔx=12.5 m，z方向間距為dΔz=5 m進行插值計算，插值后速度模型橫向網格點數為7197，縱向網格點數為3995，在相同的運算環境下，采用卷積類插值算法完成計算耗時408.972 s，采用基于速度梯度的偏微分方程插值完成計算耗時374.696 s.原模型以及插值計算后所得到的速度模型如圖4所示.通過對比插值前后的速度模型可以看出，對于速度梯度變化比較劇烈的區域，同樣由于卷積類插值算法采用的插值點數較多，忽略了原模型梯度的空間變化，插值計算后整個模型的邊緣區域變得模糊，而采用基于速度梯度的偏微分方程插值后的速度模型考慮和原模型速度梯度的空間變化，邊緣區域都得到的較好的保持.

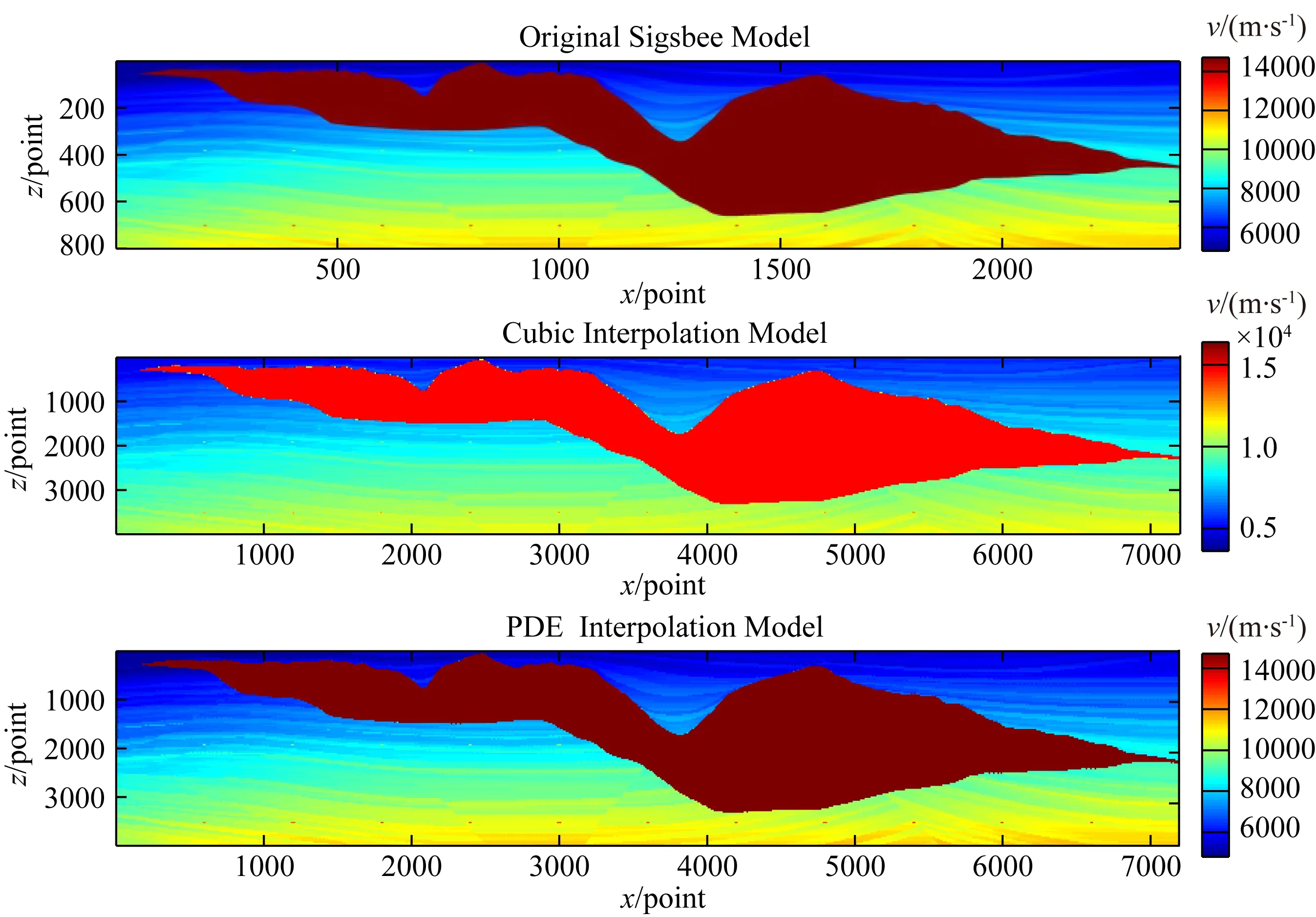
圖4 Sigsbee模型以及應用不同插值算法插值后的模型Fig.4 Original Sigsbee velocity model and its interpolation results using cubic and PDE algorithms

另外，通過插值前后的模型對比也可以看出，在速度模型底部紅色圓點區域，基于速度梯度的偏微分方程插值能夠較好的保持原始速度的局部特征，紅色圓點清晰可見，而卷積類插值后紅色圓點區域變得模糊.其主要是因為Sigsbee鹽丘模型內外速度差異比較大，速度梯度在局部變化特別明顯，卷積類插值核函數的空間不變性造成了其難以適應速度梯度變化劇烈區域的插值計算，從而造成對原模型空間結構的改變.

3 射線路徑計算

為了進一步說明偏微分方程插值的優越性，下面給出一些實際的速度模型，分別用卷積類插值和PDE插值計算射線路徑并分析其差異.

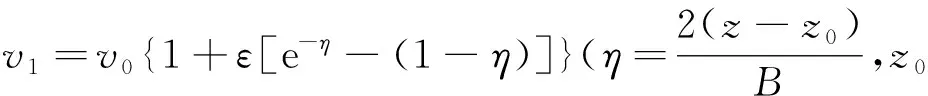
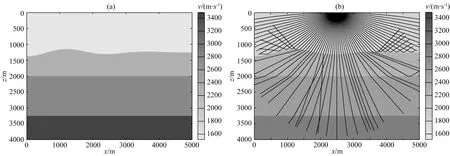
圖5 (a) 海底起伏速度模型圖； (b) 射線路徑示意圖，黑色實線為二維三次卷積插值射線路徑，虛線為偏微分方程插值射線路徑Fig.5 (a) Velocity model of seafloor relief; (b) Sketch of ray paths. The solid black line is from two-dimensional cubic convolution interpolation, and dotted line is from PDE interpolation

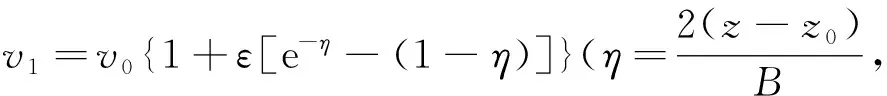
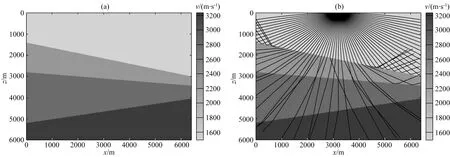
圖6 (a) 傾斜海底層速度模型； (b) 射線路徑示意圖，黑色實線為二維三次卷積插值射線路徑，虛線為偏微分方程插值射線路徑Fig.6 (a) Velocity model of inclined seafloor layer; (b) Sketch of ray paths. The solid black line is from cubic convolution interpolation, and the dotted line is from PDE interpolation

速度模型3：Marmousi速度模型：模型橫向網格點數為384，縱向網格節點數為122，橫向縱向網格間距都為24 m，射線路徑計算時間步長為0.004 s，應用二維三次卷積插值以及PDE插值計算的射線路徑如圖7所示.

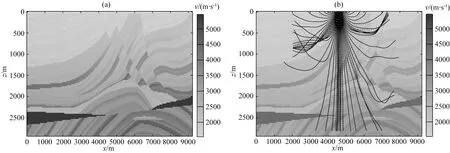
圖7 (a) Marmousi速度模型圖； (b) 射線路徑示意圖，黑色實線為二維三次卷積插值射線路徑，虛線為偏微分方程插值射線路徑Fig.7 (a) Marmousi velocity model; (b) Sketch of ray paths. The solid black line is form two-dimensional cubic convolution interpolation, and the dotted line is from PDE interpolation

從圖5—圖7的射線路徑計算結果可以看出：對于起伏海底以及傾斜層速度模型，由于每一層層速度都為常數，插值計算只發生在層與層之間，由于不同插值算法應用的插值點數以及對邊界的處理不同，應用二維三次卷積插值以及PDE插值得到的射線路徑會在在第一個分界面后存在差異；而對于速度橫向縱向劇烈變化的Marmousi 速度模型來說，由于其速度模型橫向縱向梯度變化十分明顯，因此插值點速度由于采用的插值算法不同而造成圖7b中射線路徑的差異.

4 偏移成像結果對比

下面以南海復雜的崎嶇海底大陡坡速度模型為例，驗證在射線類偏移成像中插值算法的選取對成像結果的影響.復雜的大陡坡模型橫向網格點數為3001，縱向網格點數為1501，橫向和縱向網格間距都為2.5 m，如圖8a所示.數值模擬采用炮間距500 m，共16炮，每炮601道，道間距12.5 m，時間采樣間隔2 ms.分別采用卷積類插值算法和偏微分方程插值算計算射線路徑和走時并應用高斯波束實現最終的偏移成像，偏移結果剖面如圖8b、c所示.

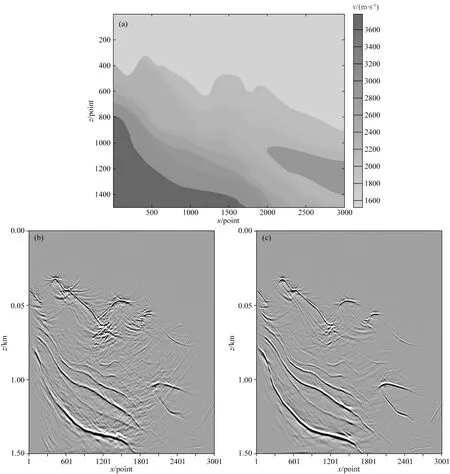
圖8 (a) 復雜的大陡坡速度模型； (b) 卷積類插值光滑處理30次后大陡坡速度模型偏移結果； (c) PDE插值光滑處理30次后大陡坡速度模型偏移結果Fig.8 (a) Velocity model of big complex steep slope; (b) Migration results of the velocity model after smoothing with two-dimensional cubic convolution interpolation; (c) Migration results of the velocity model after smoothing with PDE interpolation

從圖8的偏移成像剖面結果可以看出，對于復雜的南海某區域速度梯度變化較大的大陡坡速度模型，在射線類偏移成像當中采用基于速度梯度構建的偏微分方程插值算法對原始速度模型進行插值處理后獲得成像結果其海水底部層位清晰可見，所獲得成像效果要明顯優于采用二維三次卷積插值所獲得的偏移成像效果.

5 結論

本文針對基于彈性波傳播方程高頻近似的射線理論類偏移成像過程當中求解運動學和動力學追蹤系統當中所遇到的模型非網格節點處速度以及導數的插值問題，基于原始速度模型空間梯度變化，引入總變分最小原則，使插值點處的速度沿x方向和z方向的梯度與原始模型梯度保持一致的要求構建偏微分方程插值算子實現非網格節點處速度以及速度導數的插值計算.通過在兩個速度模型上的插值對比分析可以得出，由于偏微分方具有很好的局部特征保持特性，應用基于速度梯度構建的偏微分方程插值算法對速度模型進行插值可以較好的保持原速度模型的空間結構和邊緣特征，同時通過插值的耗時可以看出，偏微分方程插值速度要快于卷積類插值；通過不同模型的射線路徑計算可以得出，由于不同的插值算法采用的插值點不同以及對速度模型的邊緣處理不同，偏微分方程插值能更好的保持原始速度模型的空間結構，從而造成相同模型射線路徑存在較大的差異.通過圖8南海復雜的大陡坡模型的成像結果也能夠很好的說明應用基于速度梯度構建的偏微分方程插值算法對原始速度模型進行插值計算能夠在保持原始速度模型空間結構的同時可以獲得較好的成像結果.