基于密度模型稀疏表征的重力反演方法

于會臻， 王金鐸， 王千軍

中國石化勝利油田分公司勘探開發研究院， 山東東營 257000

0 引言

重力反演的目的是由地表觀測的重力數據恢復出未知地下空間的密度分布，是礦產資源勘查部署的重要手段(Paterson and Reeves，1985；Oldenburg et al.，1997；管志寧等，1998； Portniaguine and Zhdanov，1999；姚長利等，2003；孟小紅等，2012).重力反演首先需要對三維地下半空間進行離散化剖分，通常采用的方式是六面體網格方式(Li and Oldenburg，1998).但與地震、電法等地球物理技術相比，隨著深度的增加，相同大小的密度體所產生的重力異常幅值及頻率衰減更快，導致重力正演核函數矩陣條件數較大，同時受到觀測噪聲及異常處理精度的影響，反演結果分辨率較低、多解性更強.

在保證重力異常數據擬合的前提下，合理地施加模型約束項是降低重力反演多解性問題、獲得可靠密度反演結果的有效手段.不同的模型約束方法采用了不同的模型假設，以滿足不同勘探目標解釋工作的需求.Li和Oldenburg(1996)利用深度加權矩陣和L2范數約束以降低反演結果的趨膚效應；Last和Kubik(1983)引入了基于最小體積約束，Portniaguine和Zhdanov(1999)、Zhdanov(2002)、Zhdanov等(2004)引入最小支撐約束來獲得具有聚焦特征的反演結果；Bertete-Aguirre等(2002)引入了最小梯度支撐和總變差(TV)約束來保證銳化模型反演結果的邊界梯度；秦朋波和黃大年(2016)、高秀鶴和黃大年(2017)利用聚焦反演方法對重力及重力梯度數據進行聯合反演，通過融合多維度觀測信息提高反演結果可靠性；Farquharson和Oldenburg(1998)、Farquharson(2008)、Vatankhah等(2017)利用L1范數來提高反演分辨率；Sun和Li(2014)、李澤林等(2019)利用Lp范數來改善重力反演結果；彭國民等(2018)采用柯西分布約束來保證模型反演結果的稀疏性.相比來說，具有稀疏特征或稀疏邊界特征的模型約束方法能得到更高的解釋分辨率，在實際勘探應用中更具吸引力.

對于稀疏或聚焦反演方法來說，獲得可靠的結果需具備較強的前提條件：一是網格剖分與地質體間的匹配性，二是重力剩余異常求取的準確性.在實際應用中，上述條件很難得到滿足，首先地質體發育模式復雜、形態多樣，準確的網格剖分方案難以確定；其次總的重力異常為地下半空間密度體產生重力異常的疊加，背景異常難以準確剝離，獲得與聚焦密度體對應的剩余重力異常存在極大的不確定性.這些問題都會導致聚焦或稀疏約束反演密度值和空間分布與真實情況間存在較大的偏差.為此，通常可引入測井資料或添加光滑、能量最小等多種約束方式(劉展等，2011；朱自強等，2014；Utsugi，2019)來增強反演結果的可靠性，獲得介于光滑與聚焦的密度反演結果.但往往研究區測井資料有限，而且光滑與聚焦(稀疏)的聯合約束也難以描述復雜的密度空間分布.可以看出，要想滿足高精度重力反演應用需求，還需開展更深入的模型約束方法研究.

本文提出了一種新的基于密度模型稀疏表征的重力反演方法，引入了可描述典型地質體發育模式及幾何特征的特征模型，并介紹了利用特征模型構建模型特征矩陣的流程，在此基礎上，重新推導了重力反演求解方程，將直接求解密度轉換為求解與模型特征矩陣對應的分解系數稀疏求解問題，以保證利用最少的、最具有代表性的特征模型組合構成期望反演得到的密度模型，從而獲得分辨率更高、可靠性更強的三維密度反演結果.

1 方法原理

1.1 重力反演方法

首先簡要回顧一下重力反演方法.在笛卡爾坐標系下，將地下半空間剖分為三維離散網格，則重力正演可表達為如下線性方程：

AM=d,

(1)

其中，M∈Rl×1為待求解地下剖分網格內的密度模型向量，A∈Rn×l是各個剖分網格在單位密度下的重力正演核函數矩陣，d∈Rn×1為重力異常數據；n、l分別為重力觀測數據及反演區域網格剖分的個數.

重力反演是正演的逆過程，為了減少反演多解性，通常會施加定量的模型約束，可分為線性和非線性模型約束算子兩大類.前者中最為常用的包括用于保證密度模型能量最小的單位矩陣算子和保證密度模型光滑的拉普拉斯算子等；后者則在迭代反演過程中因模型的改變而改變，如最小支撐、最小梯度支撐等非線性算子.上述兩類模型約束可歸納至統一的重力反演目標函數中，形式如下：

(2)

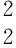
(3)

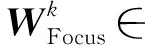
第k次迭代的密度模型Mk滿足的目標函數形式如下：

(4)

求解該目標函數的等價形式為：

(5)

其中，

ο∈Rl×1為一個零向量.

聚焦反演的目標是將密度反演結果集中在部分網格中，追求的是利用最少的密度網格模型來擬合重力數據.但異常分離不準確時，會有一定成分的區域背景異常干擾，而這部分異常對應的密度體并不符合聚焦算法的應用前提.即使異常分離結果較為準確，網格剖分過小或過大，也難以保證反演結果的可靠性.

1.2 模型特征矩陣構建流程

針對現有方法存在的問題，本文利用模型特征矩陣和分解系數來對密度模型進行稀疏表征.下面首先通過一維模型來闡述密度模型稀疏表征的含義.如圖1所示，該一維密度模型可分解為三個特征模型，一是數值為2 g·cm-3的區域背景密度模型，二是數值為0.5 g·cm-3的密度體B1剩余密度模型，三是數值為0.2 g·cm-3的密度體B2剩余密度模型.

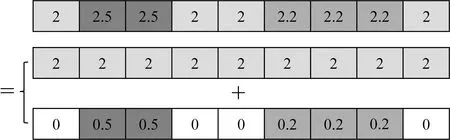
圖1 一維密度模型分解示意圖Fig.1 Diagram of 1D density model decomposition

該一維密度模型M的分解過程可表達為模型特征矩陣和分解系數向量的矩陣相乘：

(6)

其中，將D∈Rl×q稱為模型特征矩陣；Γ∈Rq×1稱為模型特征矩陣對應的分解系數向量；q為分解系數向量的個數.

矩陣D包含了三個子矩陣，即

D=[DB1,DB2,Dbg].

(7)

根據公式(6)的矩陣形式與圖1所示三個特征模型的對應關系可看出，矩陣DB1每一列包含了塊體B1的幾何形態特征，矩陣DB2每一列包含了塊體B2的幾何形態特征，矩陣Dbg包含了背景信息.為了保證利用最少的特征模型來組成密度模型，分解向量Γ應是稀疏的，其非零點處數值的大小和位置表示特征模型的密度值大小和空間賦存位置.

模型特征矩陣的構建原則來自于先驗地質假設，為更加清晰的描述模型特征矩陣構建過程，下面以二維模型(假設待反演區域沿X、Z方向剖分為9×7個網格)為例進行具體說明：

(1)根據已知資料分析，假設地質體發育模式包含以下兩類矩形塊體特征模型，具體參數為：特征模型Ⅰ(圖2a)：寬W1m、高H1m；特征模型Ⅱ(圖2b)：寬W2m、高H2m；

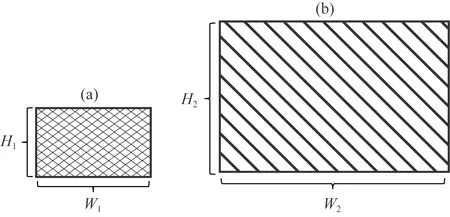
圖2 構建模型特征矩陣的特征模型(a) 特征模型Ⅰ； (b) 特征模型Ⅱ.Fig.2 Feature models for building model feature matrix(a) Feature model Ⅰ; (b) Feature model Ⅱ.

(2)首先計算特征模型Ⅰ對應的索引向量Index_I.將特征模型I的中心點坐標置于二維剖分網格左上角第一個網格(圖3a)，以此為起始點進行第1次搜索，計算特征模型I所占反演剖分的索引，索引Index_I_1位置的參數記為整數1，其余為0(圖3b)；向右平移一個網格的距離至左上角第2個網格，計算特征模型I所占反演網格的索引，并將其記錄為Index_I_2，索引Index_I_2位置的參數記為整數1，其余為0；以此類推，計算完第一層之后，從第二層的左側第一個網格點為起始點計算特征模型I的所占網格位置，并進行索引標記；之后，逐層計算，設平移至第22個網格(X=4、Z=3)(圖3c)進行第22次搜索，索引Index_I_22標記如圖(圖3d)所示；按此步驟直到遍歷所有網格；

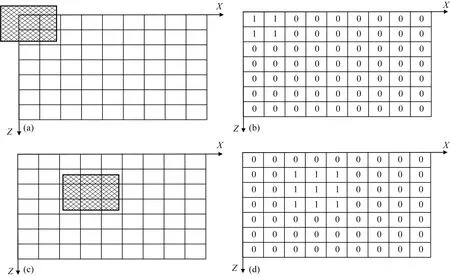
圖3 特征模型Ⅰ對應的模型特征矩陣構建過程(a) 第1次搜索位置; (b) 第1次的索引; (c) 第22次搜索位置; (d) 第22次的索引.Fig.3 Building process of model feature matrix corresponding to feature model Ⅰ(a) The first search location; (b) The first index; (c) The 22nd search location; (d) The 22nd index.

(3)將步驟(2)得到的索引Index_I_k(k=1,…,n)，n為剖分網格個數，此次為63，展開為列向量并進行組合得到特征模型I對應的模型特征矩陣DB1；

(4)特征模型Ⅱ的模型特征矩陣構建.重新執行第(2)、(3)步，計算特征模型Ⅱ下的索引向量，并將其進行組合得到特征模型Ⅱ對應的特征矩陣DB2；

(5)背景模型特征矩陣.類似特征模型Ⅰ、Ⅱ的方式，選擇具有趨勢特征的模型作為特征模型，將其生成背景模型特征矩陣Dbg；

(6)完成上述步驟，便可生成二維反演所需的模型特征矩陣D=[DB1,DB2,Dbg].

上述構建流程同樣適用于反演不等間隔網格剖分的情況.三維模型特征矩陣的構建流程與二維類似，在后文三維模型反演實驗中將舉例說明，在此不做過多贅述.

模型特征矩陣所采用的特征模型不限于規則的長方體等幾何形態，也適用于傾斜(巖脈)、球體(孤立火山巖體)等復雜地質模式特征.在實際應用過程中，可根據研究區的先驗地質認識或其他物探資料來構建模型特征矩陣.在缺少先驗地質認識的地區，也可利用重力異常分析來計算特征模型的水平和垂向上的尺寸大小及傾角信息.

相比常規反演，本文將模型特征矩陣D作用于重力正演核函數A的過程具有兩大優勢，一是相當于對原始剖分網格按照特征模型的樣式進行了重新組合，在組合后的多套網格中分別進行分解系數的稀疏求解，更加符合期望的稀疏假設條件；二是特征模型可以更高效的將期望滿足的地質模式的定性假設定量化，使得重力反演的過程更具傾向性，無論是塊狀、層狀還是傾斜狀等復雜形態的地質體發育特征都可以被引入進來.

1.3 目標函數及求解算法

將公式(6)代入公式(2)，將原重力反演問題的目標函數寫為：

(8)

其中LΓ∈Rq×q為關于分解系數Γ線性模型約束算子(取單位矩陣)；φ(Γ)為關于Γ的非線性模型約束函數.可見，基于重新構建的重力反演目標函數(8)，求解目標變為了分解系數Γ.如前文所述，為保證分解系數Γ的稀疏性，可對其施加L1范數約束項.則重力反演目標函數可寫為：

(9)

其中，‖·‖1代表L1范數稀疏約束.

稀疏求解問題在目前信號處理領域得到了廣泛的應用，求解算法包括基追蹤(Chen et al.，2001)、交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)(Boyd et al., 2010)、正交匹配追蹤(orthogonal matching pursuit)(Sahoo and Makur，2015)等.為了獲得更加高的稀疏度、更加準確的分解系數，本文采用了Majorization-Minimization(優化最小化，簡稱MM)優化框架來加速稀疏分解系數Γ的求解過程.MM框架(Figueiredo et al.，2007；Selesnick and Bayram，2014；Nguyen，2017)是用來求解非凸函數的一種性能良好的優化算法框架.MM算法通過將原來的復雜優化問題分解為一系列簡單優化問題，對于分解系數進行稀疏求解(具體推導過程見附錄A)，其第k次迭代的Γk公式如下：

(10)

WΓk-1為第k-1次迭代求解結果Γk-1對應的對角加權矩陣；φ′(Γk-1)為模型約束函數φ(Γ)關于Γk-1的一階偏導，其計算公式為：

(11)

為避免反演出現嚴重的趨膚現象，對公式(10)中的重力異常正演核函數進行深度加權，則：

(12)

其中，

Wdepth∈Rl×l為深度加權矩陣，N為深度加權參數，υ∈Rq×1為與Γ大小相等的零向量.

由于期望獲得Γ是稀疏的，即Γ中必然會出現一定數量的0值，而WΓk-1中的Γk-1位于分母位置，易出現奇異值，可對公式(10)中的求逆項進行重新推導得到如下公式.

(13)

其中，

綜合前文所述的模型特征矩陣構建及分解系數求解過程，基于密度模型稀疏表征的重力反演方法主要包含以下步驟：

(1)根據實際需求剖分原始反演網格，計算重力正演核函數矩陣A；

(2)根據工區實際情況、重力異常形態等信息設置特征模型(可包括塊體、傾斜狀巖脈、球體等各類典型地質體)，根據1.2節介紹的過程構建模型特征矩陣D；

(3)設置正則化參數λ1、λ2及深度加權參數N(一般N=4)，設置最大迭代次數IterMax；

(4)根據模型特征矩陣列向量個數設置稀疏分解系數初始模型向量Γk-1=ΓInit(k=1)，注意ΓInit不要含有0值；

(6)利用公式(10)和(13)計算第k次的分解系數Γk；

(7)利用公式(6)得到第k次迭代對應的密度模型Mk=WdepthDΓk；

(8)獲得公式(9)的計算結果，若滿足目標函數收斂條件則執行步驟(9)；若不滿足，重復步驟(5)—(7)，修改反演參數；

(9)評價(8)獲得的反演結果，若符合地質認識，則執行步驟(10)；若不滿足，重復(2)—(8)，修改特征模型，重新構建模型特征矩陣并求取反演結果；

(10)最終的密度反演結果輸出.

2 理論模型實驗分析

為了驗證本文所提重力反演方法的有效性，分別開展了二維及三維模型實驗，并與聚焦反演算法進行了對比分析.在實驗過程中均未加入密度閾值約束，即不在反演過程中限定密度的最大值和最小值.

2.1 二維模型

二維反演包括三個模型實驗，分別是無背景模型干擾的兩個地質體、存在背景模型干擾的兩個地質體和存在背景模型干擾的傾斜狀地質體.三個模型實驗均采用相同的觀測系統，具體參數為：觀測點個數為30個，間距為200 m，觀測點均位于海拔0 m.反演網格采用長方形剖分，X、Z方向剖分的個數為30×28個，網格大小為200 m×50 m，從海拔0 m向下剖分，觀測點位于第一層網格的中心位置.

(1)模型一：無背景模型干擾的兩個地質體

該模型包括兩個孤立的、不同大小的長方體(圖4b)，參數見表1.假設構造背景異常被徹底分離，即反演區域的背景密度為0 g·cm-3，模型參數見表1.觀測數據加入了3%的高斯噪聲(圖4a).

圖4 反演結果對比(a) 重力異常(黑線)及擬合數據(紅線); (b) 密度模型; (c) 常規聚焦反演結果; (d) 本文反演結果.Fig.4 Comparison of inversion results(a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper.

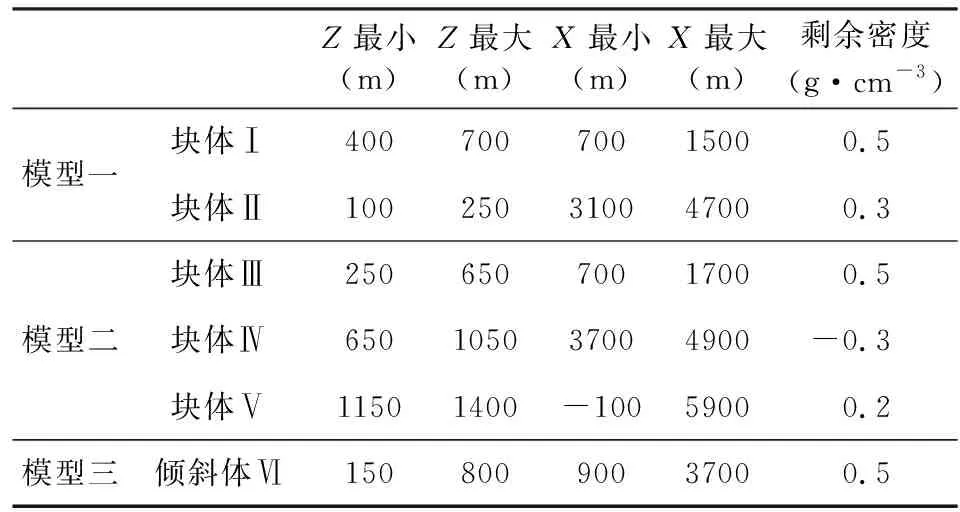
表1 二維密度模型參數Table 1 Parameters of 2D density model

構建模型特征矩陣采用了兩類模型特征矩陣構建方式，一類是選擇一個特征模型，X、Z方向尺寸為600 m×200 m的矩形密度體；另一類是選擇三個幾何形態差異較大的特征模型，X、Z方向尺寸分別為200 m×200 m，600 m×200 m，1600 m×100 m時.設置反演參數(λ1=0.1、λ2=2，最大迭代次數IterMax=150).

從該模型實驗可看出，在沒有密度閾值約束前提條件下，常規聚焦反演結果(圖4c)雖然可以較好地反映地質體質心的埋深，但是聚焦程度的控制比較難以施加，易導致反演結果過于聚焦而出現較大的密度值.利用本文所提方法進行反演，采用兩類模型特征矩陣構建方式都會得到相同的結果，如圖4d所示.可見，即使采用第二類模型特征矩陣構建方式，在分解系數稀疏約束的控制下，仍在三個特征模型中選擇了(600 m×200 m)特征模型作為待反演密度異常體的主要構成單元，與稀疏分解系數進行組合，共同恢復出了形態與密度值更接近于真實密度模型的反演結果.

(2)模型二：存在背景模型干擾的兩個地質體

該模型包括三個密度體(圖5b)，其中兩個為孤立的、不同大小、不同埋深的長方形密度體，另外一個為埋深較大的地質體(密度為0.2 g·cm-3)作為背景干擾.與模型一不同的是，兩個長方形的剩余密度體值有正、有負，具體參數見表1.在模型正演數據中加入了3%的高斯噪聲作為觀測數據(圖5a).

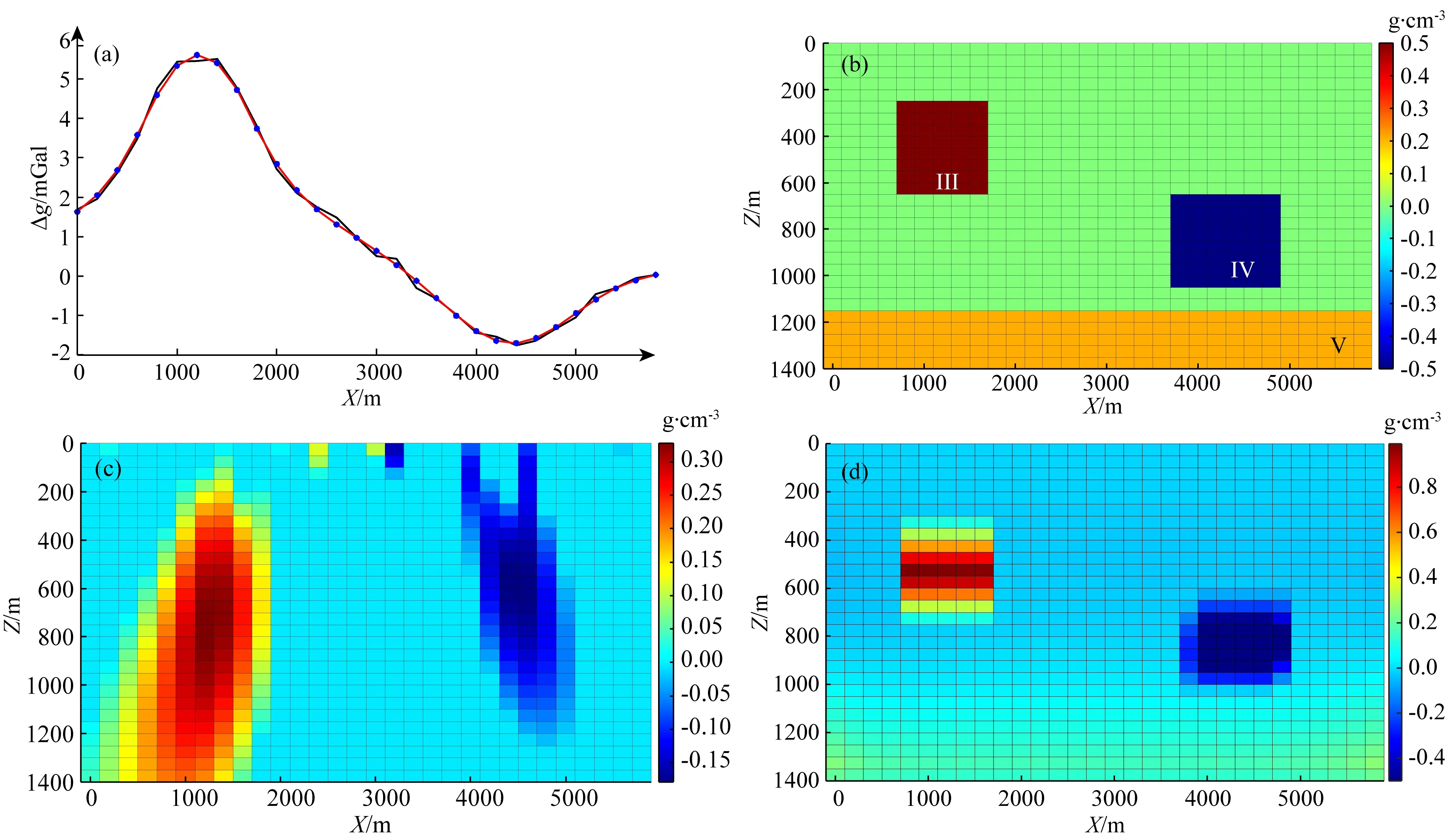
圖5 反演結果對比(a) 重力異常(黑線)及擬合數據(紅線); (b) 密度模型; (c) 常規聚焦反演結果; (d) 本文反演結果.Fig.5 Comparison of inversion results(a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper.

構建模型特征矩陣采用了四個幾何形態差異較大的特征模型，X、Z方向尺寸分別為200 m×200 m，600 m×150 m，1000 m×250 m，15000 m×100 m.設置反演參數(λ1=0.2、λ2=2，最大迭代次數IterMax=150).

從該模型實驗可看出，利用公式(5)求解得到的常規聚焦反演結果(圖5c)與原始模型偏差較大，原因主要是由于深部地質體產生的背景異常起到了干擾作用，聚焦后左側的正密度體埋深加大，結果偏向與深層背景地質體與淺層地質體之間，而右側的負密度體反演結果較淺；而從本文方法獲得反演結果(圖5d)可看出，由于模型特征矩陣構建過程中包含了水平方向長條形特征模型(15000 m×100 m)的引入，在對應的分解系數求解過程中一定程度上抵消了背景異常的干擾，相當于一個異常自動分離的過程，而其余的部分又由于包含了更接近于原始模型中塊體特征的特征模型(1000 m×250 m)，雖然結果的密度值較原有模型略大，但反演結果的空間分布更加逼近于原始模型.

(3)模型三：存在背景模型干擾的傾斜狀地質體

該模型包括一個傾斜狀的地質體，具體參數見表1.同時，與模型二類似，模擬剩余異常仍包含一定的深層信息的情形，在深部(埋深在1150～1400 m范圍內的網格)加入一個密度沿著X方向變化的橫向非均勻地質體(密度值介于0.2～0.35 g·cm-3).在模型正演數據中加入了3%的高斯噪聲作為觀測數據.

構建模型特征矩陣采用了兩種特征模型，一是傾斜地質體(圖6)，另外一類是長方形(X、Z方向尺寸為5000 m×100 m).設置反演參數(λ1=0.2、λ2=2，最大迭代次數IterMax=150).

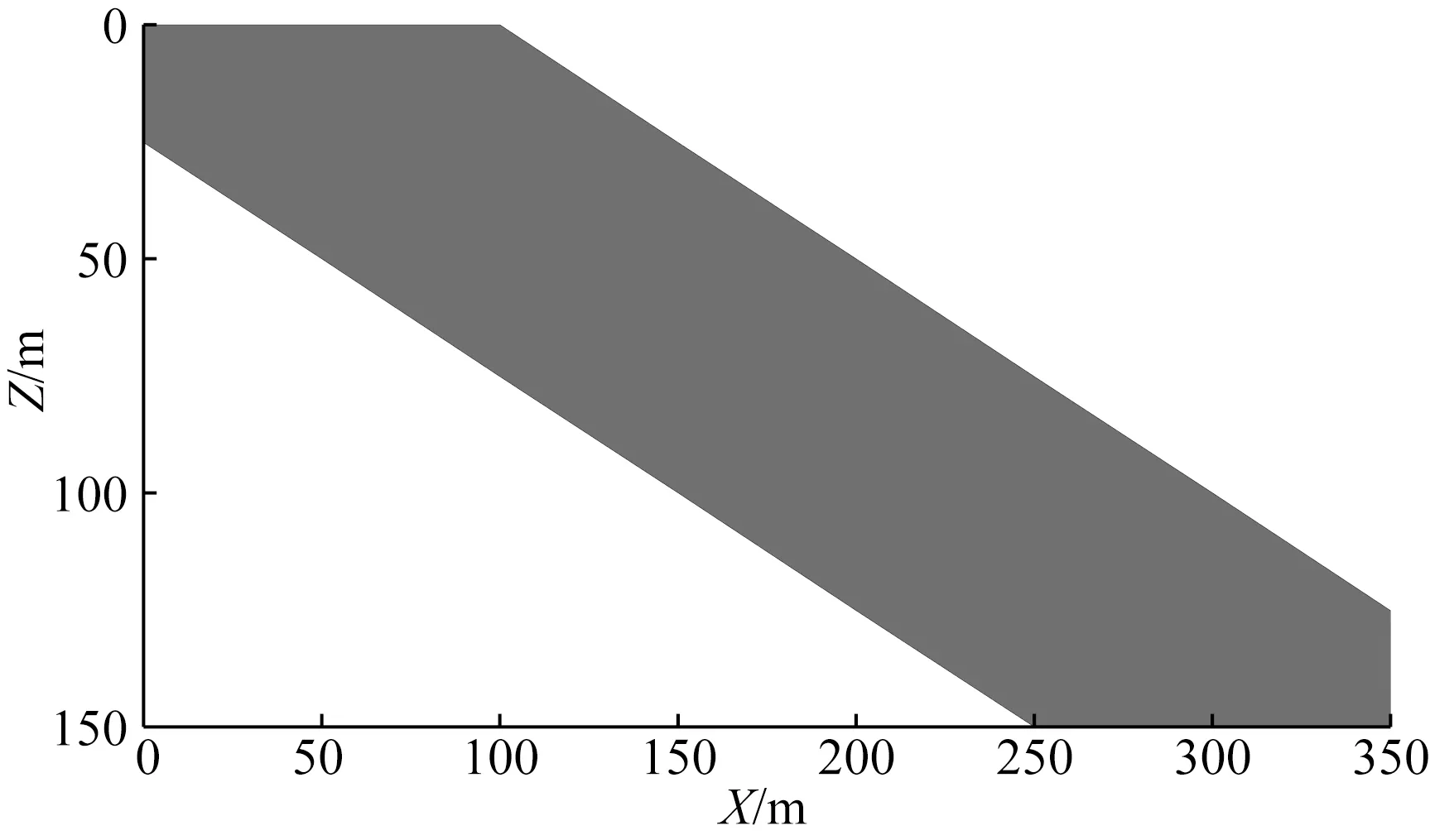
圖6 構建模型特征矩陣的二維特征模型Fig.6 2D feature model for building model feature matrix

從該模型實驗可看出，利用公式(5)獲得的常規反演結果(圖7c)雖然在一定程度上體現了傾斜狀地質體的特征，但由于深部地質體產生的背景異常的干擾，為同時保證異常的擬合以及反演模型的連續聚焦目標，使得結果埋深較大；而反觀利用本文方法得到的反演結果(圖7d)，在層狀特征模型的模型特征矩陣的聯合控制下，背景密度異常體的位置得到較好的恢復.同時，具有傾斜形狀的特征模型(與模型大小并不相同)的引入又大大增加了逼近原始模型的可能性，使得即使沒有在反演過程中控制密度閾值范圍，恢復的淺層傾斜狀地質體密度值及空間分布也與原始模型十分接近.

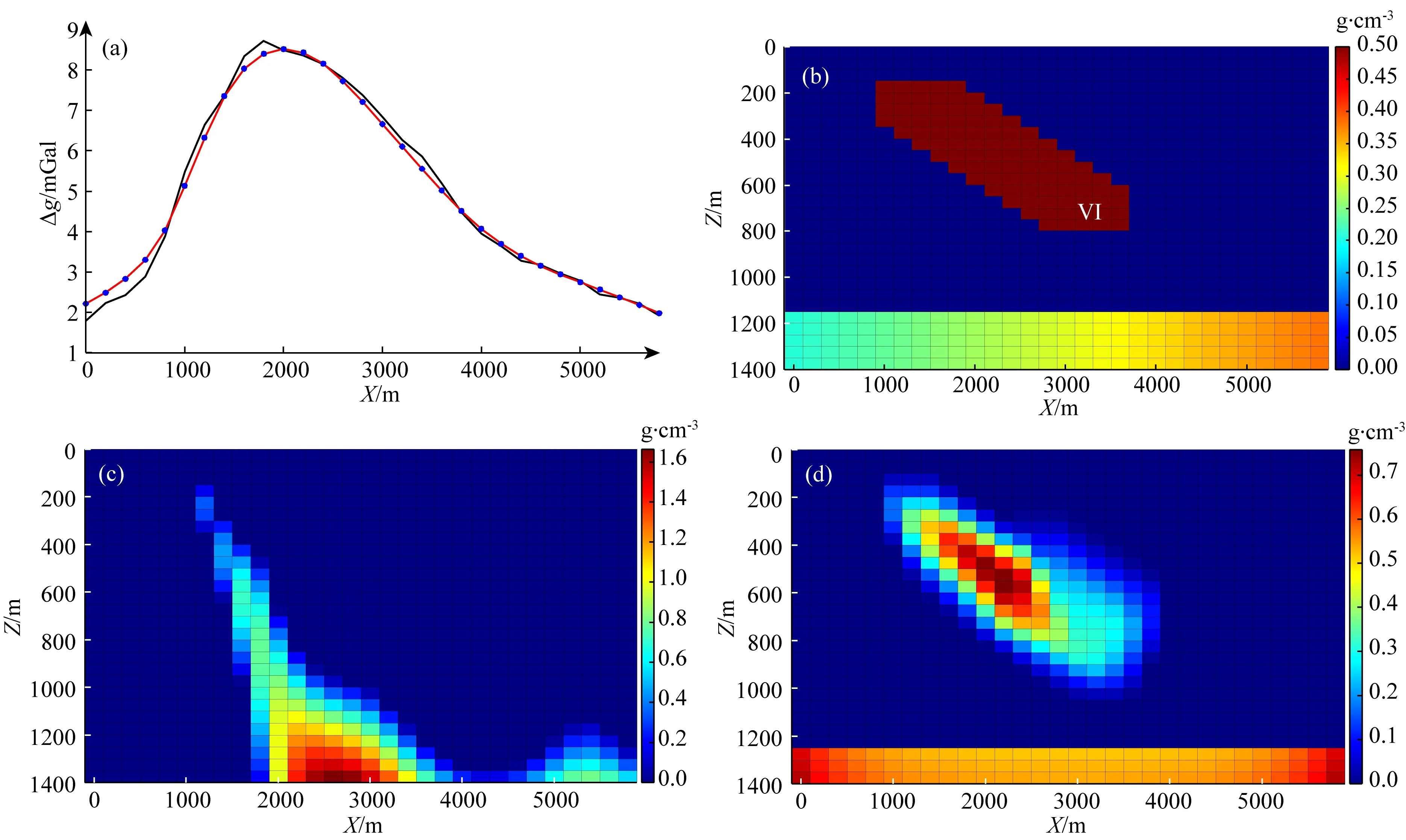
圖7 反演結果對比(a) 重力異常(黑線)及擬合數據(紅線); (b) 密度模型; (c) 常規聚焦反演結果; (d) 本文反演結果.Fig.7 Comparison of inversion results(a) Gravity anomaly (black line) and fitting data (red line); (b) Density model; (c) The results of conventional focus inversion; (d) The results of this paper.

2.2 三維模型

三維模型反演實驗中，重力觀測系統在X、Y方向的間距為200 m，觀測網格X、Y方向的個數為20×20=400個.反演網格采用長方體剖分，剖分網格在X、Y、Z方向的大小為200 m×200 m×200 m，反演網格在X、Y、Z方向剖分為20×20×10=4000個網格單元.三維模型形態呈“Y”字型，由2個傾斜狀地質體構成，如圖8a所示，參數見表2.三維密度模型正演模擬獲得的數據添加了3%的噪聲作為觀測數據，如圖8b所示.

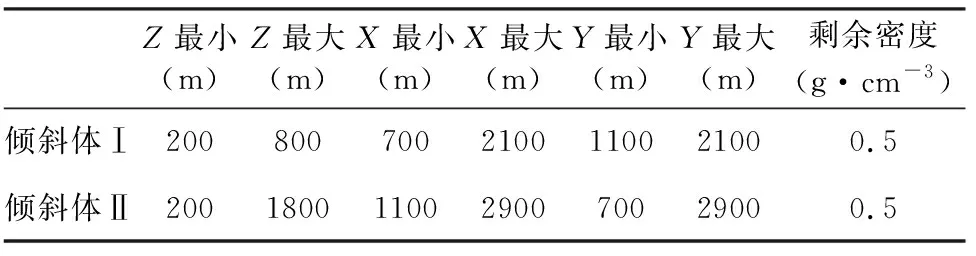
表2 “Y”字型地質體密度模型參數Table 2 Parameters of Y-type geological body density model

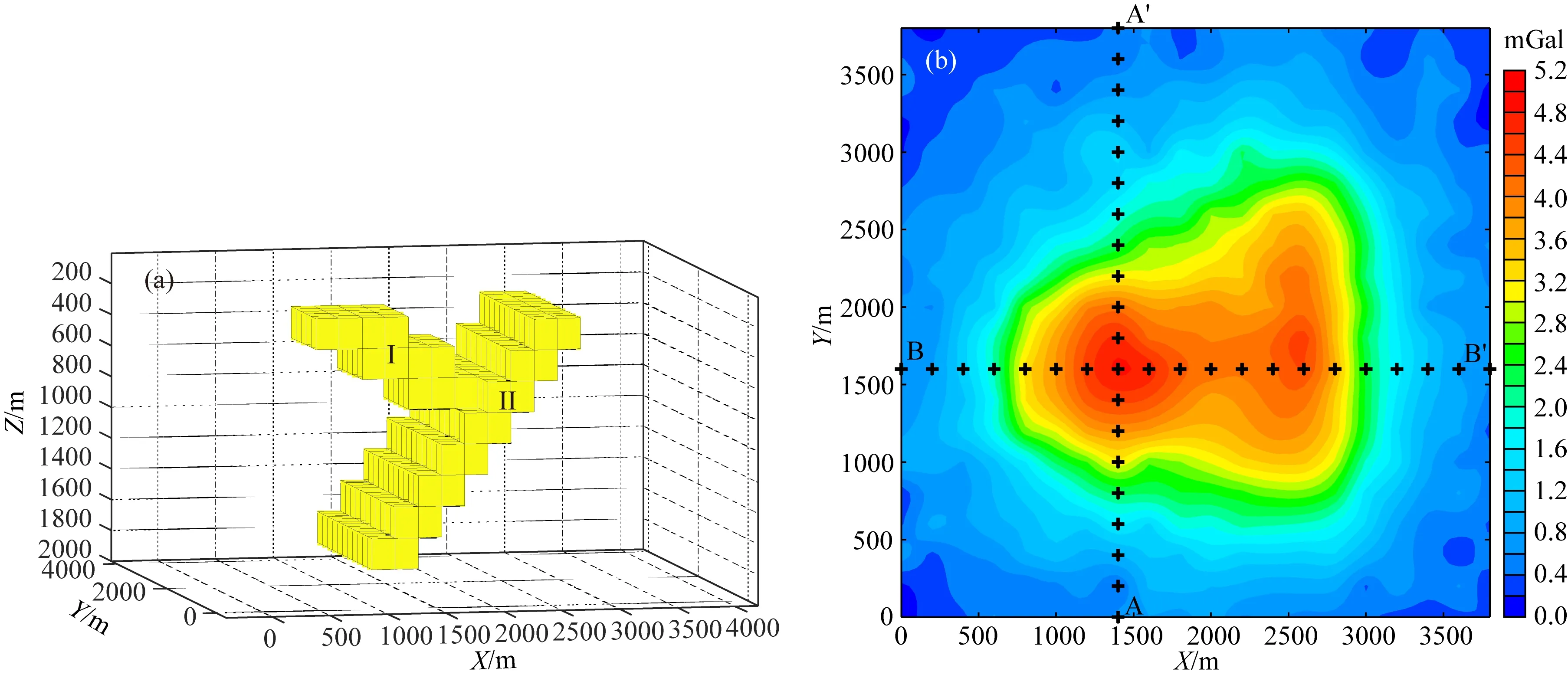
圖8 三維密度模型及重力異常(a) 三維密度模型； (b) 重力正演異常(含3%高斯噪聲).Fig.8 3D density model and gravity anomaly(a) 3D density model; (b) Gravity forward anomaly (including 3% Gaussian noise).

構建模型特征矩陣采用了兩個三維特征模型，一是沿X軸正方向的向上右傾的三維特征模型a，如圖9a所示，另一個是沿X軸反方向的向上左傾的三維特征模型b，如圖9b所示.設置反演參數(λ1=1、λ2=1，最大迭代次數IterMax=200).

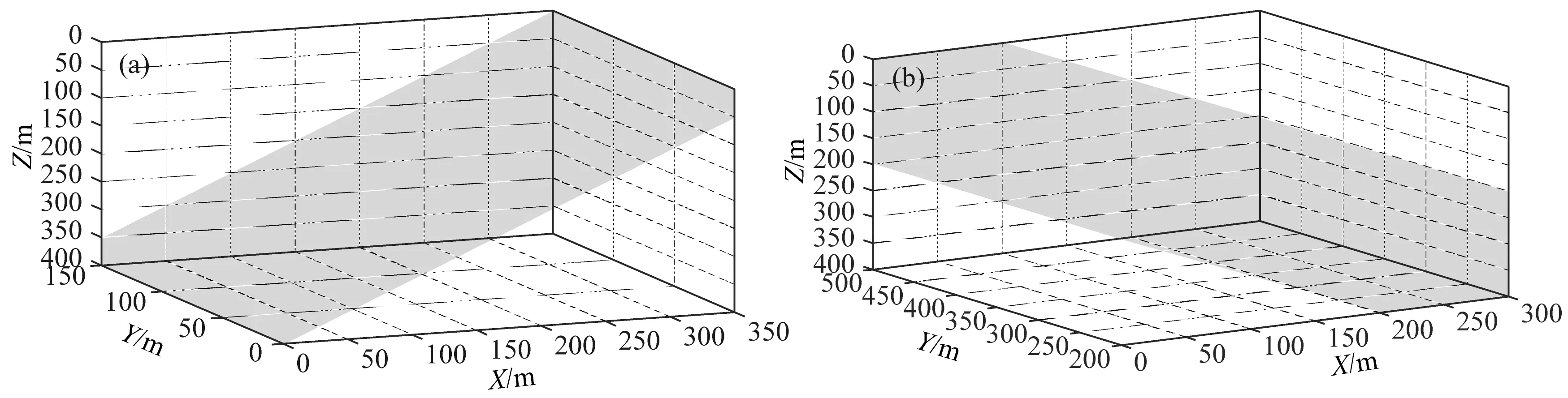
圖9 構建模型特征矩陣的三維特征模型(a) 三維特征模型a； (b) 三維特征模型b.Fig.9 3D feature model for building model feature matrix(a) 3D feature model a; (b) 3D feature model b.

從該模型實驗可看出，利用公式(5)獲得的常規反演結果(圖10c、圖10d)雖然在中心埋深上與模型比較接近，且一定程度上體現了“Y”字型特征，但反演結果分辨率較低，且傾斜體II的形態與埋深均得不到較好的恢復；而觀察本文方法得到的反演結果(圖10e、圖10f)，雖然構建模型特征矩陣的兩類傾斜形狀特征模型并非與真實模型的傾斜異常體大小相同，但包含接近的傾斜狀發育特征，該約束信息的引入使得反演過程中更加注重傾斜狀密度異常體的生成，使得反演結果逼近原始模型的可能性大大增加，即便沒有施加密度閾值約束，模型的分辨率與形態特征都與原始模型保持更高的一致性.

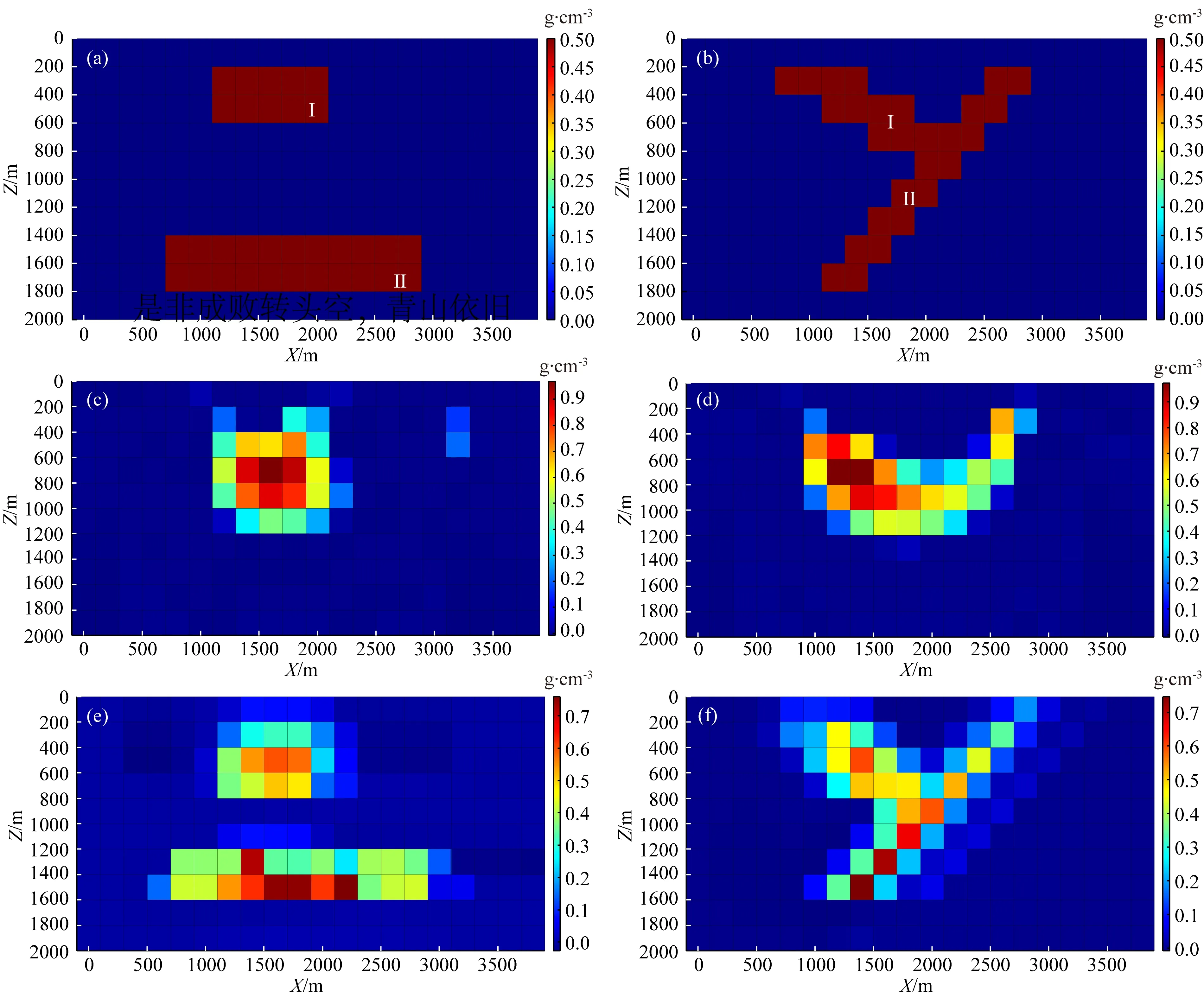
圖10 反演結果對比(a) 理論模型A-A′垂直剖面； (b) 理論模型B-B′垂直剖面； (c) 聚焦反演A-A′垂直剖面； (d) 聚焦反演B-B′垂直剖面； (e) 本文方法A-A′垂直剖面； (f) 本文方法B-B′垂直剖面.Fig.10 Comparison of inversion results(a) A-A′ profile of theoretical model; (b) B-B′ profile of theoretical model; (c) A-A′ profile of focus inversion; (d) B-B′ profile of focus inversion; (e) A-A′ profile of proposed method; (f) B-B′ profile of proposed method.

通過二維及三維模型實驗可看出，相比常規反演方法，利用本文所提方法得到的反演結果在分辨率和可靠性方面都得到了有效提升.

雖然在進行分解系數求解時，未知數的個數會有所增加，但是特征模型的引入反而在一定程度減少了密度模型的求解空間，這是由于期望獲得的密度模型不僅需要考慮正演結果與實測數據的擬合，還需要滿足由盡可能少的特征模型來組合得到；而且從重力異常解釋效率的角度來看，本文所提方法可更加靈活、快速地施加密度模型約束信息，無需反復調整網格剖分方案及過多地調整重力異常分離參數，在一定程度上克服了求解分解系數帶來的計算量增加的問題.

3 實際資料應用測試

現將本文方法應用于墨西哥薩卡特卡斯州圣尼古拉斯硫化物銅鋅礦區的重力實際資料.研究區的礦床賦存于鎂鐵質和長英質火山巖中，根據鉆井及巖心資料可知該硫化物礦床具有高密度、高磁化率、高極化率和低電阻率的特點(Phillips et al.，2001)，其中密度可達3.5 g·cm-3，較圍巖大概有1.1～1.4 g·cm-3的密度差，且埋深較淺，便于利用重力勘探技術預測礦床的空間分布.工區重力測點數為198個，將其利用克里金插值為均勻網格異常(圖11a)，X(東西，-2700～-600 m)、Y(南北-1100～600 m)方向間距分別為100 m、100 m，觀測網格X、Y方向的個數為22×18=396個.

利用本文方法開展重力三維反演.首先將地下半空間沿X、Y、Z三個方向剖分為22×18×15=4000個網格單元，尺寸為100 m×100 m×100 m.第一個網格的位置X、Y、Z坐標位于(-2750 m，-1150 m，0 m).構建模型特征矩陣采用了三個長方體特征模型，在X、Y、Z方向的尺寸分別為300 m×300 m×300 m、800 m×200 m×400 m和1800 m×1200 m×200 m，前兩個特征模型用于構建局部密度異常體，第三個特征模型用于擬合均勻的背景剩余密度.給定的分解系數初始模型為0.1，設置反演參數(λ1=1、λ2=1，最大迭代次數IterMax=200).

利用本文方法獲得的密度反演三維結果如圖11b所示，經過礦床的南北A-A′的垂向剖面如圖11c所示，東西向垂直剖面B-B′如圖11d所示，密度反演結果與根據鉆井資料獲得的硫化物礦床地質認識(Phillips et al.，2001)十分吻合.對比國內外研究學者在該礦區開展的工作(Lelivere and Oldenburg，2009；李澤林等，2019)，反演結果在其他區域也恢復出了具有較高分辨率且更易解釋的密度分布，有效驗證了本文方法的適用性.分析原因，模型特征矩陣中引入的背景特征模型使得在三維反演結果中產生了較為合理的背景密度模型，在一定程度上消除了區域異常分離不準確的問題.與此同時，在分解系數的稀疏求解過程中，不同尺寸的特征模型得到優選，并用來逼近目標密度體，使得反演的可靠性得到了保證.進一步的，在實際資料應用中，針對不斷細化的勘探工作需求，可嘗試構建更精細的特征模型及模型特征矩陣，從而不斷提升重力反演分辨率，逐步恢復出更符合真實情況的地質體密度空間分布.

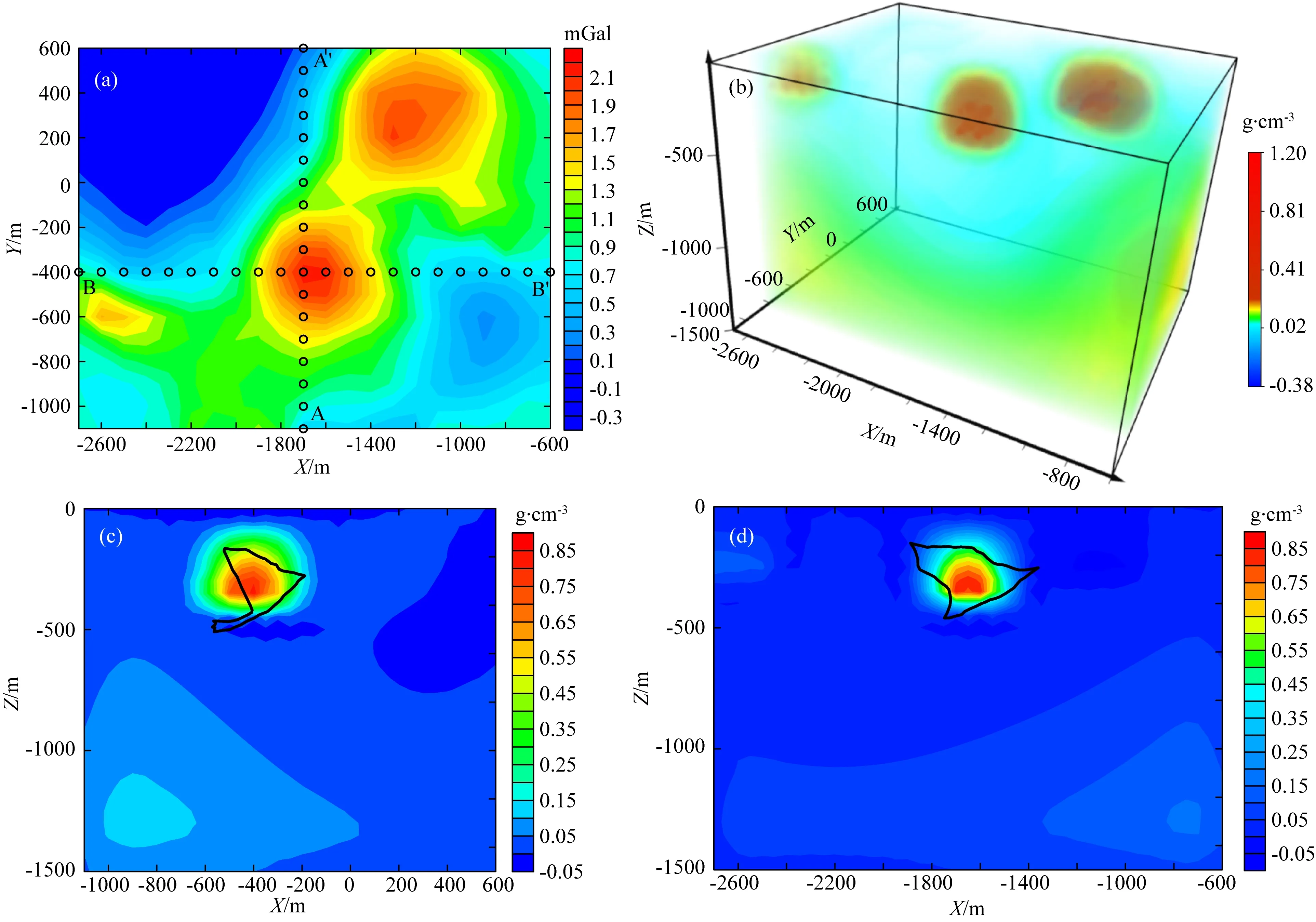
圖11 實際資料反演結果(a) 剩余重力異常; (b) 密度三維反演結果; (c) A-A′垂直剖面反演結果； (d) B-B′垂直剖面反演結果. (c)—(d)中黑色多邊形代表硫化物礦床的位置.Fig.11 Inversion results of actual data(a) Residual gravity anomaly; (b) 3D inversion result of density; (c) The result of A-A′ vertical profile; (d) The result of B-B′ vertical profile.The sulphide location is indicated by the black polygon in (c)—(d).

4 結論

本文提出了一種基于密度模型稀疏表征的重力反演方法.首先，將密度模型表征為模型特征矩陣和分解系數的乘積，其次，給出了由特征模型構建模型特征矩陣的技術流程，再次，重新構建重力反演目標函數，將直接求解密度模型問題轉換為求解分解系數，最后，給出了分解系數的稀疏求解方法，實現了可有效融合地質模式信息、提高重力反演分辨率和可靠性的目的.理論模型實驗和實際資料應用測試表明，相比常規聚焦反演算法，在反演目標包含多個地質體或剩余異常無法準確求取時，本文方法都可取得較好的應用效果.此外，本文所提出的模型約束方法并不僅限于重力反演，也為磁力、電法、地震等其他地球物理反演方法提供了一種靈活添加地質約束信息的有效途徑.

致謝感謝三位匿名評審專家和期刊編輯對本文提出的寶貴修改意見.

附錄A 基于Majorization-Minimization優化框架的分解系數稀疏求解

根據正文1.3節中公式(8)，原重力反演問題的目標函數寫為關于分解系數Γ的最優化目標函數：

(A1)

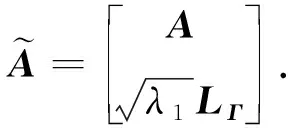
由于在稀疏求解時，φ(Γ)通常為一不可微的凸函數，現定義函數G(Γ)形式為：

G(Γ)=a·Γ2+b,

(A2)

其中，a、b為常數.

可知函數G(Γ)是關于Γ的嚴格凸函數.

根據MM框架理論，可知在待求的Γ=Γv處，G(Γv)應滿足如下假設：

(A3)

其中，Γv表示第v次迭代所對應的Γ值.

將公式(A3)代入公式(A2)，則

(A4)

其中，a和b為常數項.

求解方程組(A4)，可得a和b.

(A5)

將公式(A5)代入公式(A2)，G(Γ)可寫為：

(A6)

若Γ、Γv都為大小為q×1的向量，則根據MM思想：

(A7)

設

(A8)

其中，WΓv為與第v次迭代求解結果對應的對角加權矩陣，c為與Γv有關的數值.

(A9)

因此，原目標函數(A1)可表示為：

(A10)

對其求最小二乘解，可得：

(A11)