信息源在香濃熵及鄧熵中的應(yīng)用原理

摘 要：在量子決策中，一個(gè)事件發(fā)生的概率無(wú)法單一使用實(shí)數(shù)來(lái)表示。從薛定諤的貓到人類決策。一個(gè)事件伴隨著多種狀態(tài)。故需要引入復(fù)數(shù)來(lái)表示這類事件，它也被叫做信息源。香濃熵及鄧熵作為一種信息融合方式，表示一組數(shù)據(jù)的相關(guān)程度，混亂程度。用信息源表示鄧熵，要解決復(fù)數(shù)在香濃熵和鄧熵公式中的運(yùn)用，以及所得結(jié)果的數(shù)學(xué)意義。

關(guān)鍵詞：量子決策;信息源;香濃熵

一、復(fù)數(shù)概率的量子性

量子概率來(lái)源于量子物理，但不一定要用來(lái)描述微觀粒子，而是去描述更一般的宏觀系統(tǒng)，如人類的認(rèn)知現(xiàn)象。從數(shù)學(xué)的角度上來(lái)講，就是將概率取復(fù)數(shù)這個(gè)特點(diǎn)切入到量子概率的理論體系中。量子概率可以說(shuō)是將經(jīng)典概率擴(kuò)展到復(fù)數(shù)域之后的數(shù)學(xué)產(chǎn)物，故整個(gè)量子概率體系的結(jié)論都可以自然得到。

量子概率可以解釋成經(jīng)典概率在復(fù)數(shù)域的擴(kuò)充，其實(shí)刻畫的是觀察者對(duì)于外界信息的不確定情況下的描述。這種不確定要比經(jīng)典概率不確定更不確定：一個(gè)是量子概率考慮到了觀察對(duì)觀測(cè)系統(tǒng)的影響，也考慮到觀察者處理信息能力的極限。

量子概率的最主要的特點(diǎn)是不兼容屬性-指一個(gè)客觀物體所具備的兩種屬性，這兩種屬性不能同時(shí)得到確切的測(cè)量值。其中可以用不確定性原理來(lái)解釋。具體說(shuō)是我們對(duì)兩個(gè)屬性 A 和 B 的認(rèn)識(shí)存在著局限性，如果我們對(duì) A 取某值的信念程度越高，我們對(duì) B 取值的看法就會(huì)變得更模糊不清。

例如，由于我們?nèi)祟惖挠^察、信息處理能力有限，在某一個(gè)特定時(shí)刻，我們掌握了 A 屬性的性質(zhì)，也就必然會(huì)伴隨著對(duì) B屬性的不掌握。如我們看到了月球的正面，就看不到其反面。故正反面就構(gòu)成了一對(duì)不兼容的屬性，并呈現(xiàn)出不確定的關(guān)系。

二、信息源在量子化DS證據(jù)理論中的形態(tài)

Dempster-Shafer證據(jù)理論作為對(duì)處理未知的信息與模型的時(shí)候要比經(jīng)典證據(jù)理論更加靈活。這種未知與量子概率的不確定性相似。因此，在識(shí)別框架下的mass（質(zhì)量）函數(shù)除了可以用DS證據(jù)理論表示，還應(yīng)可以在量子理論基礎(chǔ)上進(jìn)行表示。

量子識(shí)別框架下的mass函數(shù)：

如圖所示，要用信息源（|q1>與|q2>）表示一個(gè)證據(jù)事件對(duì)于兩個(gè)信念|A>與|B>的支持度。

量子框架下的mass函數(shù)與DS類似：

Q（|A>）=γeiθ? ?Q（Φ）=0

其中量子框架下的mass函數(shù)Q（|A>）也可以被稱作QBPA，叫信息源。

三、香農(nóng)熵和鄧熵的介紹

香農(nóng)信息熵，解決了對(duì)信息的量化度量問(wèn)題。一條信息的信息量大小和它的不確定性有直接的關(guān)系。比如我們要搞清楚一件非常不確定的事，就需要了解大量的信息。相反，如果對(duì)某件事已經(jīng)有了較多的了解，我們不需太多的信息就能把它搞清楚。從這個(gè)角度，我們可認(rèn)為，信息量的度量等于不確定性的多少。

香農(nóng)熵 H（U）=E[-logpi]=-Σni=1PilogPi

該公式表示，變量的不確定性越大，熵就越大，所需要的信息量也就越大。

香農(nóng)熵可以度量一個(gè)概率分布的不確定度和信息容量，是信息論的基礎(chǔ)。證據(jù)理論中的基本概率指派（Basic Probability Assignment， BPA），作為視作對(duì)概率分布的一種推廣。如何度量BPA的不確定度和信息容量，仍然是一個(gè)有待解決的問(wèn)題。針對(duì)該問(wèn)題，提出了一種基本概率指派的熵—鄧熵。

Ed （m） = -A? ? X m（A）log2 m（A）/2|A|-1;

當(dāng)BPA從冪集退化為單子集上的概率分布時(shí)，鄧熵退化為香農(nóng)熵。

四、香濃熵與鄧熵在mass函數(shù)中的應(yīng)用與區(qū)別

Ed （m） = -A? ? X m（A）log2 m（A） /2|A| - 1

給出一個(gè)識(shí)別框架 X = {a， b， c}，已知它們的質(zhì)量mass函數(shù)值為 m（a） = m（b） = m（c） = 1/3， 得到香濃熵和鄧熵均為1.585：（香濃熵和鄧熵在單子集所得的結(jié)果一致

給定一個(gè)辨識(shí)框架 X={a，b}，對(duì)于這個(gè)辨識(shí)框架的質(zhì)量函數(shù)為m1（a，b）=1

則鄧熵表示為

Ed （m）=-log21/22-1

此時(shí)無(wú)法用香農(nóng)熵來(lái)表示。

五、香農(nóng)熵與鄧熵的信息源表示

在辨識(shí)框架Ω={|A>，|B>，|C>}下，有單元素信息源如下

Q（|A>）=0.574eiθ1

Q（|B>）=0.574eiθ2

Q（|C>）=0.574eiθ3

則香農(nóng)熵鄧熵均為

-（0.574eiθ1log20.574eiθ1+0.574eiθ2log20.574eiθ2+0.574eiθ3log20.574eiθ3

根據(jù)對(duì)數(shù)公式和歐拉公式可以得出

-0.574eiθlog20.574eiθ=-0.574（cosθ+isinθ）[ln（0.574）+i（θ+2nπ）]

展開(kāi)得到

-0.574[ln（0.574）（cosθ+isinθ）+θ（icosθ-sinθ）]

-0.574[ln（0.574）ejθ+θe-i（θ-1/2π）]

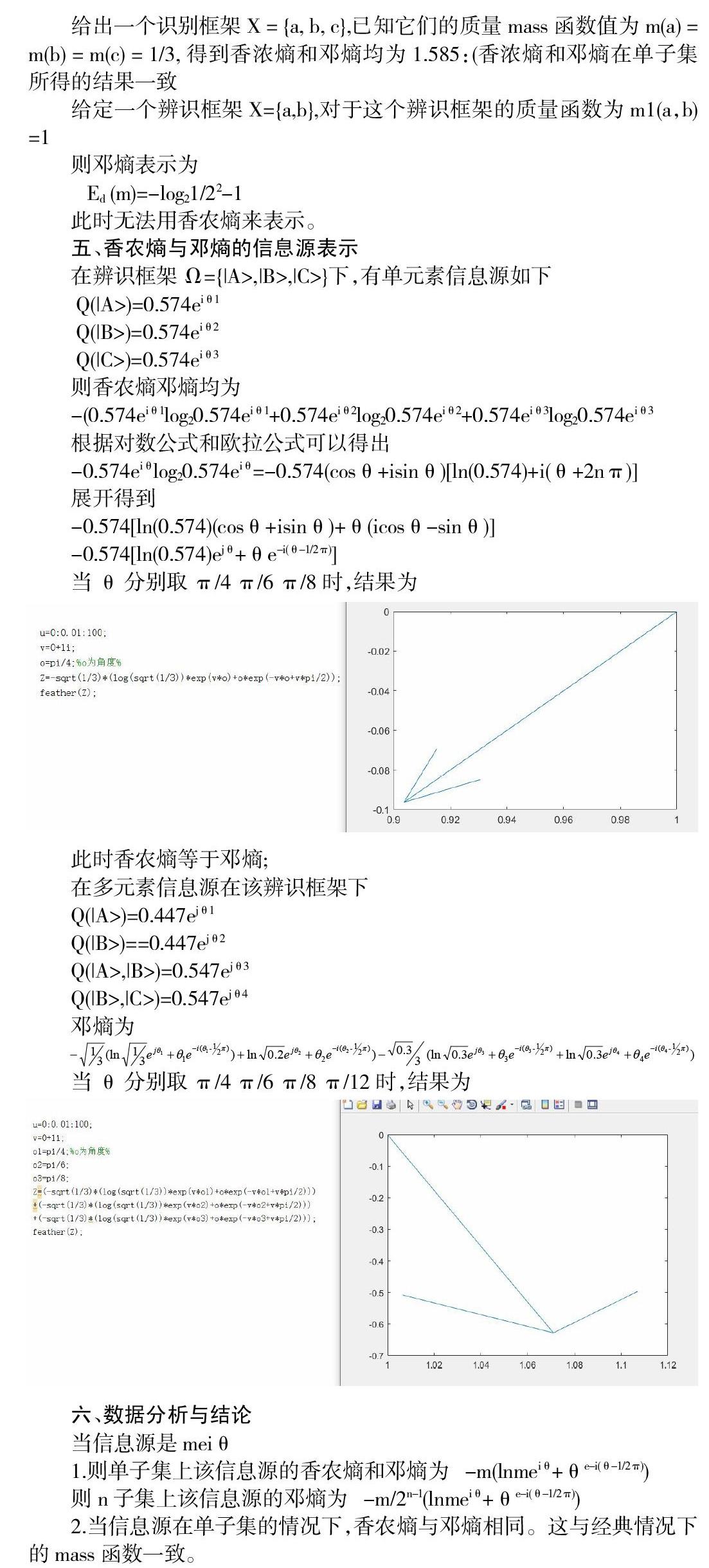
當(dāng)θ分別取 π/4 π/6 π/8時(shí)，結(jié)果為

此時(shí)香農(nóng)熵等于鄧熵;

在多元素信息源在該辨識(shí)框架下

Q（|A>）=0.447ejθ1

Q（|B>）==0.447ejθ2

Q（|A>，|B>）=0.547ejθ3

Q（|B>，|C>）=0.547ejθ4

鄧熵為

當(dāng)θ分別取 π/4 π/6 π/8 π/12時(shí)，結(jié)果為

六、數(shù)據(jù)分析與結(jié)論

當(dāng)信息源是meiθ

1.則單子集上該信息源的香農(nóng)熵和鄧熵為? ?-m（lnmeiθ+θe-i（θ-1/2π））

則n子集上該信息源的鄧熵為? ?-m/2n-1（lnmeiθ+θe-i（θ-1/2π））

2.當(dāng)信息源在單子集的情況下，香農(nóng)熵與鄧熵相同。這與經(jīng)典情況下的mass 函數(shù)一致。

而信息源擴(kuò)充到多子集的時(shí)候，只有鄧熵可以表示該信息源。

3.關(guān)于θ的探究

每個(gè)信息源而言，θ獨(dú)立，變化范圍在0-360之間。

θ與m無(wú)具體的聯(lián)系，且與概率信念無(wú)關(guān)，表示的并不是信息源與坐標(biāo)軸的夾角。

參考文獻(xiàn)：

[1]X.Z. Gao and Y.Deng ”Quantum model of mass function” WILEY Int J Intell Syst. 2020;35;267-282.;

[2]Y.Deng “不確定性度量的新方法” 陜西西安：陜西師范大學(xué). 2019.6.18

[3]Pan Y， Zhang L， Li Z， Ding L. Improved fuzzy bayesian network‐based risk analysis with interval-valued fuzzy sets and d‐s evidence theory. IEEE Trans Fuzzy Syst. 2019：1-1. https：//doi.org/10.1109/TFUZZ.2019. 2929024

作者簡(jiǎn)介：

劉榮政（2001.06- ）男，漢族，遼寧沈陽(yáng)人，西南大學(xué)計(jì)信院自動(dòng)化專業(yè)，本科在讀，主要研究方向?yàn)樾畔⑷诤吓c決策。