基于狀態變量分析的船舶主機控制系統傳感器偶發性故障檢測

李奇鐘，朱慧敏，譚笑，張瑞，薛晨，習文

（震兌工業智能科技有限公司，廣東 深圳 518101）

0 引言

近年來，隨著電子、信息等技術的高速發展，一種不同于傳統持續故障形式的特殊故障類型，即偶發性故障逐漸引起了人們的重視。偶發性故障是指一類持續時間有限，沒有外部補償措施仍然可以自行消失使系統重新恢復可接受性能的故障。

目前，對船舶主機控制系統的故障檢測已成為熱點研究課題。然而多年來，人們大多僅關注持續故障的檢測問題，而偶發性故障檢測問題研究較少。船舶主機控制系統由復雜電子電路構成，虛焊老化等都會導致控制電路松動進而引發控制器偶發性故障。此外，船舶主機控制系統運行環境復雜，傳感器易受震動、電磁干擾等影響，導致傳感器偶發性失效。

隨著偶發性故障的積累，最終失效無法自行消失而影響主機控制系統的正常工作，對船舶安全構成嚴重威脅，如果能在偶發性失效轉化為永久性失效之前就提前檢測到傳感器的異常，提前予以修復或更換，便可以避免更大的經濟損失和安全風險。船舶主機上布置有多種傳感器，其所監測的物理量對于船舶主機的工況（通常用轉速表征）都有不同程度的貢獻，主機的工況（輸出）正是由這些物理量構成的狀態向量及狀態方程所決定的，其非線性動態系統可簡化為如下模型[1]。

規范變量分析是一種動態過程監控和分析的技術，通過最大化歷史和未來數據集之間的相關度來獲取系統的特征信息，并進一步建立系統的統計模型。如果某傳感器傳回的讀數相較于正常值間歇性發生明顯偏移，則認為傳感器可能發生了偶發性故障。基于這種思路，本文提出了一種能夠對船舶主機控制系統的傳感器偶發性故障進行準確檢測的方法和系統。

1 CVA檢測模型

基于CVA算法的故障診斷技術最早由Negiz和Cinar在1997年提出[2]，文獻［3-4］對CVA在故障檢測中的應用做了詳細的介紹。

CVA作為一種子空間算法能有效處理高階多變量系統，能直接從數據中辨識狀態變量的特性使其適用于多變量系統。

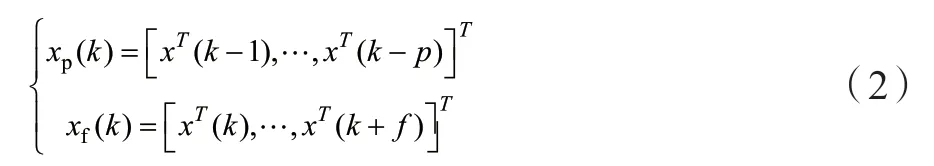
（2）按照一定的準則如交叉驗證法，確定規范變量的個數f，p。

（3）求標準化后的數據矩陣Χf、ΧP的協方差和互協方差矩陣，并執行奇異值分解：

（4）根據給定的置信水平a，設置狀態空間霍特林統計量和殘差空間霍特林統計量的閾值和[5]：

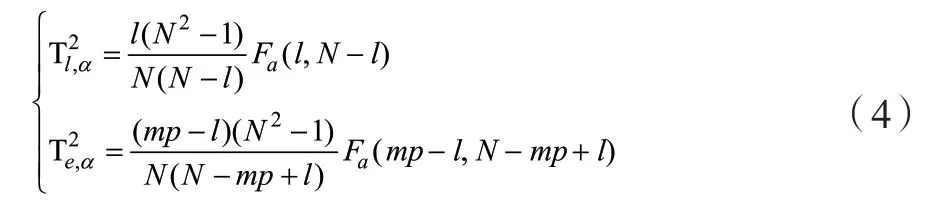
其中l為保留的狀態個數，U1包含了U的前l列，Ue包含了U的最后mp-l列，為從數據中提取的CVA狀態。

（5）實時檢測故障時，取一段時間的實時數據進行標準化，在線計算兩種統計量：

若結果超出（4）中的閾值，則認為發生了故障。

CVA算法屬于故障診斷方法中的多變量統計的方法，與CVA類似的還有包括PCA、PLS、FDA等常見算法[6]，但由于船舶主機的各種變量之間往往具有強烈的自相關性和互相關性，使得考慮變量相關性最大化的CVA從多種多變量統計算法中脫穎而出。雖然DPCA和DFDA等算法通過對原有的基礎算法進行改進，考慮狀態變量的時滯性，但對于自相關性較強的系統仍然容易顯得力不從心[7]。同時，考慮到對傳感器偶發性故障檢測的實時性要求，我們需要選擇一種計算代價小、效率高的算法，而CVA以其只需要計算一次奇異值分解的理論優勢超越了其他許多同類算法[8]。綜上所述，我們最終選擇了CVA算法作為故障檢測的基礎算法。

近年來，CVA及其改進算法往往用于化工過程的故障檢測，相關的工作大多在公開的數據集比如田納西-伊斯曼（TE）化工過程仿真平臺[6,9-15]和模擬青霉素生產過程[16]產生的數據上進行仿真和研究，研究者從算法的魯棒性[17]、時變性[10]等各個角度予以創新，但很少脫離化工過程的模型進行仿真，這一方面是出于化工過程往往有清晰的狀態方程可以用于理論驗證，另一方面缺少其他工業過程的數據集也導致難以開展仿真工作。王寶祥[18]利用CVA算法對滾動軸承退化過程監測，得到振動信號故障特征之后再用經驗模態法（EMD）進行分解，再從模態的角度予以分析，對于將CVA算法用于非化工過程有很好的指導意義。

2 實驗與結果分析

2.1 數據來源及實驗流程

我們采集了本公司經營的一條二十萬噸級貨運船出廠后一年內的航行數據。由于船上的設備均為全新，我們取第一周的數據作為正常樣本，將后半年航行的數據作為測試樣本，用于檢測是否存在控制系統傳感器偶發性故障。算法流程圖如圖1所示。為了提升算法的準確性，我們將所有傳感器的數據均進行去均值和方差歸一化的預處理。

值得注意的是，由于CVA本身只關注對主機狀況貢獻較大的一些特征變量，可能會舍棄部分貢獻較小的變量，通過控制前l個變量的累積貢獻率達到95%以上，被舍棄的變量對于主機控制系統無足輕重，即使傳感器發生了故障，其對主機控制系統的決策的影響也微乎其微，甚至我們可以據此去掉一些不必要的傳感器。

圖1 故障檢測流程

我們的數據包含船主機氣缸上多個傳感器的讀數。具體變量情況如表1所示。

表1 變量編碼表

2.2 結果與分析

利用CVA方法，首先可以根據各變量的貢獻率選出特征變量，其中各變量的貢獻率如圖2所示。為了驗證算法的正確性，我們也用了動態主成分分析（Dynamic Principal Component Analysis, DPCA）算法計算出了各變量的貢獻率（如圖3所示），通過對上述兩種方法的比較，可以看出對于主要特征變量的選擇是一致的。

圖2 CVA方法下各變量的貢獻率

圖3 DPCA方法下各變量的貢獻率

從中選取貢獻率累積超95%的前l個變量，可得l=19。后續統計量閾值畫線，我們只針對這19個特征變量進行。由于奇異值分解時一些小量的倒置，導致統計量可能過于敏感，故只有當連續3個采樣點都超過閾值，才認為發生了故障[5]。在某段時間內19個變量的兩種T2統計量以及相應閾值畫線如圖4所示。由此可見氣缸排氣溫度、滑油出口壓力、燃油進出口溫度三種物理量對應的傳感器最容易發生偶發性故障，這可能與其惡劣的工作環境有關。

為了進一步驗證CVA方法的準確性，我們采用在高關聯度數據集上常用的DPCA算法對同一數據集進行分析，將兩種算法的結果進行比較。DPCA算法需要預先設定最大延時，延時越大則考慮數據時序相關性越充分，結果越準確，但計算效率也更低。當延時超過某個閾值（在系統的物理最大延時附近）時，其檢測結果趨于穩定。通過計算，本數據集的物理最大延時大約在30個單位時間，保險起見，取延時為50個單位長度的DPCA模型檢測結果作為標準，各模型的相對準確率及在同一單核CPU上的運行時間如表2所示。從中可以看出，CVA利用很小的算量開銷，達到了較大延時下DPCA模型的同等效果，這也從側面印證了CVA適用于高關聯性數據分析的理論優勢。

圖4 變量1-22（除去9,15,19）的兩種統計量以及相應閾值

表2 不同模型下的檢測準確率和程序運行時間

3 結論

（1）CVA方法適用于從船舶主機控制系統的多維傳感器數據中提取特征變量，可以找出對主機工作狀態有主要影響的物理量，利用相應的統計量閾值設置算法，可以排查出傳感器的偶發性故障。

（2）和PCA方法相比，CVA方法考慮了數據的自相關性和互相關性，更適用于對來自船舶主機傳感器組等高維強關聯數據的分析；DPCA方法雖然也考慮了數據的時序相關性，但計算效率不及CVA，后者更加適用于實時故障檢測。

（3）實例分析表明，基于CVA的數據分析方法，為船舶主機控制系統傳感器偶發性故障檢測提供了新思路，在實船數據上表現出較高的準確性，具有較為廣闊的應用前景。