改進的Whipple 防護結(jié)構(gòu)與相關(guān)數(shù)值模擬方法研究進展*
陳 瑩,陳小偉
(1. 北京理工大學(xué)機電學(xué)院,北京 100081;2. 北京理工大學(xué)爆炸科學(xué)與技術(shù)國家重點實驗室,北京 100081;3. 北京理工大學(xué)前沿交叉科學(xué)研究院,北京 100081)
隨著科技發(fā)展,人類對宇宙的探索更加頻繁,如何幫助航天器有效應(yīng)對太空環(huán)境中的各種威脅,受到人們的廣泛關(guān)注。航天器在實際運行過程中,對于尺寸大于10 cm 的碎片或隕石等障礙物,通常采用主動規(guī)避的方式。10 cm 以下的小型碎片基本無法探測,需安裝防護結(jié)構(gòu)以抵御這種威脅。早期,防護結(jié)構(gòu)的主要防護對象為體積較小的微流星體等,而航天活動帶來的太空垃圾以及每次碰撞產(chǎn)生的新碎片使得太空環(huán)境中的空間碎片數(shù)量不斷增加,航天器生存環(huán)境持續(xù)惡化。根據(jù)空間碎片的來源與類型統(tǒng)計,2008-2018 年間,已觀察到增加了近6 800 個在軌碎片(總數(shù)超過11 500 個)[1]。空間碎片碰撞已成為近地空間結(jié)構(gòu)的主要威脅,這些碎片的大小從亞毫米到幾十厘米不等,速度范圍為0~15 km/s。通常將尺寸介于1~10 cm 的碎片稱為危險碎片,其平均撞擊速度為10 km/s[2]。當它直接作用于航天器時,將導(dǎo)致結(jié)構(gòu)板穿透等嚴重損傷甚至失效,對航天器的安全運行造成威脅。針對空間碎片問題,我國載人航天器已成功進行首次空間碎片防護工程應(yīng)用,載人航天器的“空間碎片行動計劃”專項研究工作已取得一定成果,但與國際先進技術(shù)相比還存在差距[3-4]。因此,開展航天器防護研究工作,降低或避免空間碎片撞擊帶來的危害,對于提高航天器的安全性、穩(wěn)定性,延長航天器的壽命具有重要意義。
Whipple 防護結(jié)構(gòu)最早提出于1947 年[5],已被實踐證明是保護航天器免受超高速撞擊破壞的有效手段。傳統(tǒng)的Whipple 防護結(jié)構(gòu)為單層板結(jié)構(gòu),由間隔一定區(qū)域的均質(zhì)金屬板作為前板和后板組成,如圖1所示,其中v 為彈丸速度,S 為前后板間距。結(jié)構(gòu)中前板主要起緩沖作用,彈丸超高速撞擊前板時,彈丸破碎與前板損傷產(chǎn)生的碎片共同形成碎片云團,從而減少航天器外壁承受的沖擊載荷。以球形彈丸正撞擊為例,碎片云結(jié)構(gòu)可分為反濺碎片云、碎片云外泡和碎片云主體3 部分[6],如圖2 所示。高速撞擊在彈丸和前板中產(chǎn)生沖擊波,能量隨著沖擊波的傳播而釋放,部分以熱量形式散發(fā),整體溫度升高。沖擊波傳播到彈、板自由表面時反射形成拉伸波,導(dǎo)致彈板破碎。其破碎顆粒大小與原始沖擊速度的大小成反比[7],同時與沖擊波波前形狀和自由表面幾何形狀呈函數(shù)關(guān)系,這兩個參數(shù)主要由撞擊過程中彈丸的形狀和方向控制[8-9]。在足夠高的沖擊速度下,部分碎片會發(fā)生熔化、氣化現(xiàn)象,碎片云更易膨脹[10]。
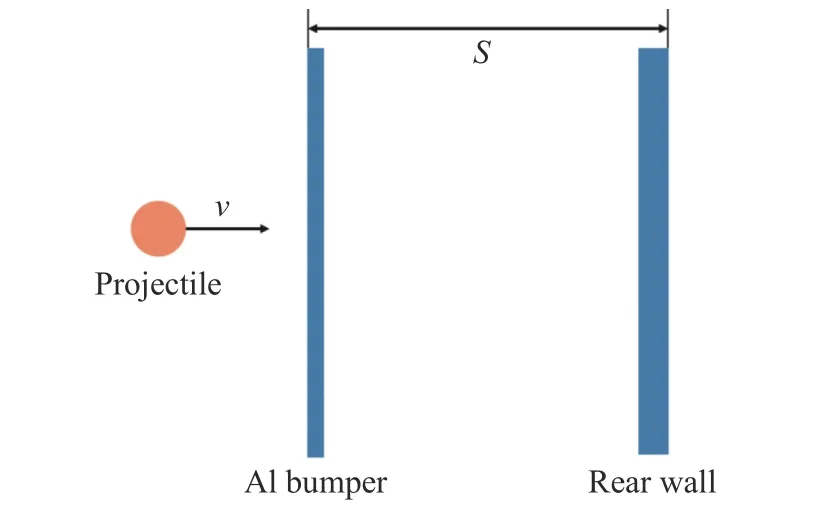
圖1 Whipple 防護結(jié)構(gòu)[5]Fig. 1 Whipple shield[5]

圖2 碎片云結(jié)構(gòu)(球形彈丸)[6]Fig. 2 Debris cloud structure (spherical projectile)[6]
由于受到Whipple 防護結(jié)構(gòu)應(yīng)用條件的限制,其材料和結(jié)構(gòu)應(yīng)滿足以下條件:首先,結(jié)構(gòu)應(yīng)具有足夠的防護能力,能根據(jù)要求保護航天器的關(guān)鍵表面;其次,結(jié)構(gòu)質(zhì)量受限,應(yīng)盡量減少影響航天器運行的額外質(zhì)量。隨著近地軌道環(huán)境的惡化,傳統(tǒng)的Whipple 防護結(jié)構(gòu)在一定程度上已經(jīng)無法滿足航天器所需的防護強度要求。因此,發(fā)展更先進的Whipple 防護結(jié)構(gòu)尤為必要。學(xué)者們通過試驗、測試及數(shù)值模擬等方法,通過改變防護板結(jié)構(gòu)和材料對Whipple 防護結(jié)構(gòu)進行優(yōu)化,提出了多層板結(jié)構(gòu)[11-13]、填充式結(jié)構(gòu)[14]、夾芯板結(jié)構(gòu)[15-16]、波紋緩沖板[17-18]等。隨著高性能材料的不斷發(fā)展,防護結(jié)構(gòu)性能的提高更依賴于材料的改變和涂層材料的應(yīng)用等方面,材料的多樣性使得Whipple 結(jié)構(gòu)的改進有更多可能。目前在航天器的空間碎片防護研究中,經(jīng)試驗證明可應(yīng)用的防護材料有鋁板[5]、Nextel 纖維布[10]、Kevlar 纖維布[10]、聚碳酸酯[19]、Nextel/Kevlar 纖維布[14]、聚亞安酯泡沫[3]、聚苯并咪唑(PBI)薄膜涂層[20]、C/SiC 復(fù)合材料[21]、Al/PTFE 高能材料[22]等。這些材料的應(yīng)用可有效提高Whipple 防護結(jié)構(gòu)的防護能力。
防護結(jié)構(gòu)的防護能力通常由彈道極限方程(ballistic limit equation,BLE)描述,當彈丸直徑超過臨界界限時,防護結(jié)構(gòu)將失效。彈道極限方程最早于1969 年由Cour-Palais[23]給出,將能夠直接反映防護結(jié)構(gòu)實際物理損傷的彈丸臨界直徑與撞擊參數(shù)、結(jié)構(gòu)參數(shù)等的關(guān)系進行定義。1992 年,Christiansen[12]為彈丸的沖擊速度劃分區(qū)間,給出了與試驗數(shù)據(jù)更相符的三段式方程。2001 年,Christiansen[24]對三段式方程進行修正,得到了目前應(yīng)用最廣的彈道極限方程。根據(jù)彈丸破碎狀態(tài),可將低、中、高速度區(qū)間分別視為彈道區(qū)、破碎區(qū)、熔化/氣化區(qū)。彈道區(qū)沖擊速度較低,此時彈丸尚未破碎,臨界直徑隨著沖擊速度的增大而減小,后板損傷也隨之增大。破碎區(qū)的標志在于形成碎片云,碎片云膨脹后與后板撞擊,沖擊速度越高、碎片云徑向膨脹越大,對后板侵徹能力降低,臨界直徑增大。撞擊速度增大時,彈丸與前板碰撞破碎,隨著溫度升高,部分碎片可能產(chǎn)生熔化/氣化,臨界直徑隨沖擊速度增大而減小。不同構(gòu)造的Whipple防護結(jié)構(gòu)的彈道極限方程也不盡相同[25],鄭建東等[26]認為前板與后板的厚度比也是影響方程中3 段區(qū)域分界點大小的關(guān)鍵因素。彈道極限方程的優(yōu)化和應(yīng)用對航天器的防護設(shè)計與性能評估具有重要意義。
本文中將針對Whipple 防護結(jié)構(gòu)發(fā)展過程中幾個重要的結(jié)構(gòu)變化,闡述不同結(jié)構(gòu)的防護機理,列出相應(yīng)的彈道極限方程,對比分析其力學(xué)性能和防護能力。結(jié)合相關(guān)材料的超高速撞擊試驗以及數(shù)值模擬結(jié)果,梳理其對應(yīng)的碎片云撞擊下的破壞模式,對不同結(jié)構(gòu)和材料的彈道能力和結(jié)構(gòu)性能進行對比。同時,總結(jié)數(shù)值模擬方面的研究進展,為防護結(jié)構(gòu)的未來研究方向提出建議。
1 多層板結(jié)構(gòu)
傳統(tǒng)的Whipple 防護結(jié)構(gòu),前板為單層均質(zhì)金屬板,對于較大尺寸的空間碎片,其防護效果較差。為實現(xiàn)碎片的多次加載,學(xué)者們提出了多層板防護設(shè)想[11-13]。即在等質(zhì)量前提下,將前板替換成多層薄板,各層之間有一定間隔,形成(最基本的)多層板結(jié)構(gòu),可使碎片與板進行多次碰撞,碎片得到充分加載,從而降低其侵徹能力。然而,純金屬多層板無法兼顧防護結(jié)構(gòu)的強度和質(zhì)量要求,多種高性能材料的應(yīng)用為結(jié)構(gòu)設(shè)計提供了新思路和更多可能性。
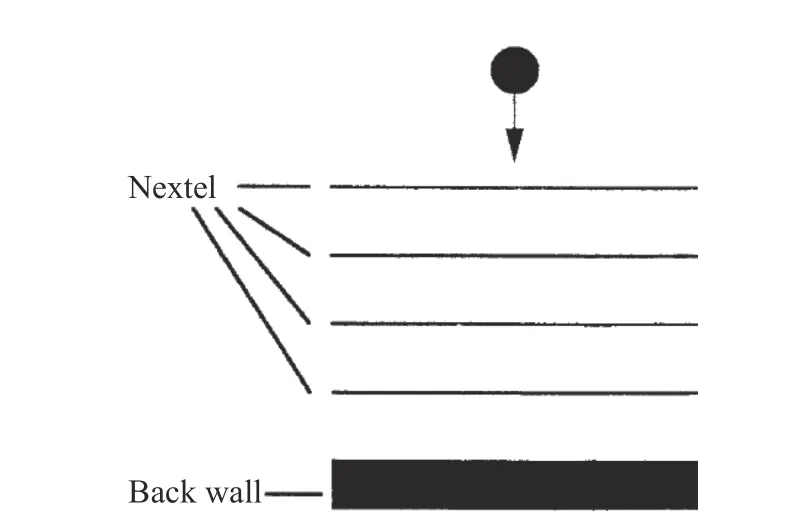
圖3 Multi-shock (MS)防護結(jié)構(gòu)[10]Fig. 3 Multi-shock shield[10]
1.1 Multi-shock (MS)防護結(jié)構(gòu)
1990 年,Cour-Palais 等[11]提出了MS 防護結(jié)構(gòu),使用多層相同的Nextel 陶瓷織物材料替代金屬前板,其結(jié)構(gòu)如圖3 所示。Nextel 陶瓷織物具有超薄、柔韌、強度高等特點,對應(yīng)的防護板質(zhì)量較輕,且在碰撞過程中產(chǎn)生碎片較少。彈丸在高速撞擊首層薄板時發(fā)生破碎,彈丸碎片與板碎片以碎片云的形式繼續(xù)撞擊隨后的幾層薄板,整體溫度升高。板間距為碎片云的膨脹提供了一定空間,在撞擊下一層薄板前,碎片云的侵徹能力逐步減弱,每一次撞擊都將消耗動能并使得碎片尺寸減小。因此,與單層防護結(jié)構(gòu)相比,MS 防護結(jié)構(gòu)可將碎片提升到更高的壓力和熱狀態(tài),起到更好的防護作用。
試驗表明,彈丸以6.3 km/s 的速度撞擊MS 防護結(jié)構(gòu)時,碎片云熔化和汽化的比例與以10 km/s 的速度撞擊傳統(tǒng)Whipple 防護結(jié)構(gòu)相當[11]。因此,MS 防護結(jié)構(gòu)的防護性能與傳統(tǒng)單層板結(jié)構(gòu)相當,但能減輕40%以上的結(jié)構(gòu)總質(zhì)量[13]。
1.2 Mesh double-bumper (MDB)防護結(jié)構(gòu)
Crews 等[13]和Christiansen 等[12,27] 提出了MDB 防護結(jié)構(gòu),如圖4 所示。與MS 防護結(jié)構(gòu)不同,MDB 防護結(jié)構(gòu)采用不同材料組成多層板防護結(jié)構(gòu),如網(wǎng)狀板、金屬板與Kevlar/Spectra 纖維布,且各層板的作用不同。
不同材料的前板可分層逐步消耗彈丸能量。鋁線網(wǎng)[27]具有密度低、質(zhì)量輕的特點。彈丸先與第1 層鋁線網(wǎng)撞擊并初步破碎,溫度升高[28]。此時彈丸碎裂程度較低,已產(chǎn)生的碎片擴散,與彈丸主體一起繼續(xù)運動至與第2 層均質(zhì)薄板(Gr/Ep 或Al 板)相撞。均質(zhì)薄板強度較鋁線網(wǎng)更高,可使彈丸破碎更徹底,有利于碎片云的進一步形成和擴張;第3 層為Kevlar/Spectra 纖維布,其質(zhì)量輕、強度高,被撞擊時產(chǎn)生的碎片較少,可有效減緩碎片速度,消耗動能。多層不同材料的防護板結(jié)構(gòu)可降低碎片云的侵徹能力,令后板能夠承受剩余載荷。沖擊試驗表明,MDB 防護結(jié)構(gòu)比相同質(zhì)量的普通雙層鋁板結(jié)構(gòu)防護性能更優(yōu)。
彈道極限方程是衡量結(jié)構(gòu)防護能力的重要標準,當彈丸以速度v 沖擊多層板防護結(jié)構(gòu)時,MS 和MDB 多層板結(jié)構(gòu)的彈道極限方程分別表示為[12]:
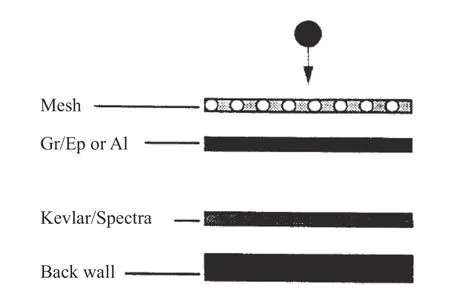
圖4 Mesh double-bumper(MDB)防護結(jié)構(gòu)[10]Fig. 4 Mesh double-bumper shield[10]

式(1)適用于由4 個Nextel 防護板和均質(zhì)鋁后板組成的MS 防護結(jié)構(gòu),防護板之間的間距相等。式(2)適用于以Kevlar/Spectra 纖維布作為中間層的MDB 防護結(jié)構(gòu)。
1999 年,Christiansen 等[29]對多種多層板防護結(jié)構(gòu)進行了試驗評估,與傳統(tǒng)Whipple 防護結(jié)構(gòu)相比,多層板防護結(jié)構(gòu)可有效降低結(jié)構(gòu)總質(zhì)量,防護性能得到優(yōu)化。但多層板結(jié)構(gòu)較為復(fù)雜,應(yīng)用具有一定的局限性。研究結(jié)果表明,當前后板間距與彈丸直徑的比值S/D≥30 時,MS 和MDB 的防護性能最好。但在航天實際應(yīng)用中,體積限制要求S 較小(S≈11 cm,S/D<11)[14],不能滿足最佳的空間要求,多層板結(jié)構(gòu)配置無法達到最優(yōu),對防護能力提升有限。同時,防護結(jié)構(gòu)的質(zhì)量限制使得各層防護板的厚度較薄,即使能夠?qū)崿F(xiàn)多次加載,其強度仍存在改進空間。
2 填充/夾芯板結(jié)構(gòu)
傳統(tǒng)的Whipple 防護結(jié)構(gòu)與多層板防護結(jié)構(gòu)均存在一定缺陷。在二者研究基礎(chǔ)上,學(xué)者們通過進一步改進結(jié)構(gòu)設(shè)計,提出了一種填充式防護結(jié)構(gòu)[14]:以均質(zhì)鋁板為前板,在結(jié)構(gòu)中心位置填充一層厚度較大的防護板,填充部分稱為中間層。中間層可對碎片云進行二次加載并保證等質(zhì)量下板的強度,這種結(jié)構(gòu)可有效地提高防護能力。
金屬泡沫、金屬蜂窩等吸能材料的密度低,應(yīng)用于航空航天領(lǐng)域可有效降低整體結(jié)構(gòu)的質(zhì)量。為彌補其強度不足的缺陷,可將較高強度的金屬板與金屬泡沫[15]、金屬蜂窩[16]等材料相結(jié)合,組成夾芯式防護板,將其應(yīng)用于Whipple 防護結(jié)構(gòu)。填充式防護結(jié)構(gòu)與夾芯板防護結(jié)構(gòu)較為典型,應(yīng)用廣泛。
2.1 填充式防護結(jié)構(gòu)
2.1.1 NextelTM/KevlarTM填充式防護結(jié)構(gòu)
1995 年,Christiansen 等[14]提出了填充式Whipple 防護結(jié)構(gòu)SW(stuffed Whipple),以均質(zhì)金屬板作為前板,在前后板間隔的中間位置選取可有效減輕結(jié)構(gòu)質(zhì)量并具有良好防護能力的材料作為中間層。如圖5 所示,SW 結(jié)構(gòu)采用陶瓷纖維布(NextelTM)和高強度復(fù)合材料纖維布(KevlarTM)組成NextelTM/KevlarTM中間層,比填充等質(zhì)量的實心鋁防護板具有更好的防護效果[24]。
彈丸撞擊前板形成的碎片云與中間層碰撞被二次加載,添加的MLI(multi-layer insulation)層與鋁網(wǎng)結(jié)構(gòu)可使碎片云進一步擴散,NextelTM陶瓷纖維布能夠比鋁板更有效地破壞彈丸及碎片云。同時,KevlarTM纖維布的比強度比鋁更高,可有效減緩碎片云速度,降低碎片云與后板碰撞的損害。在同等條件下,NextelTM/KevlarTM填充材料在碰撞過程中產(chǎn)生的碎片由于纖維直徑較小而尺寸較小,相比于均質(zhì)金屬材料產(chǎn)生的碎片,侵徹能力更低。
適用于球形鋁彈丸撞擊SW 防護結(jié)構(gòu)的彈道極限方程為:
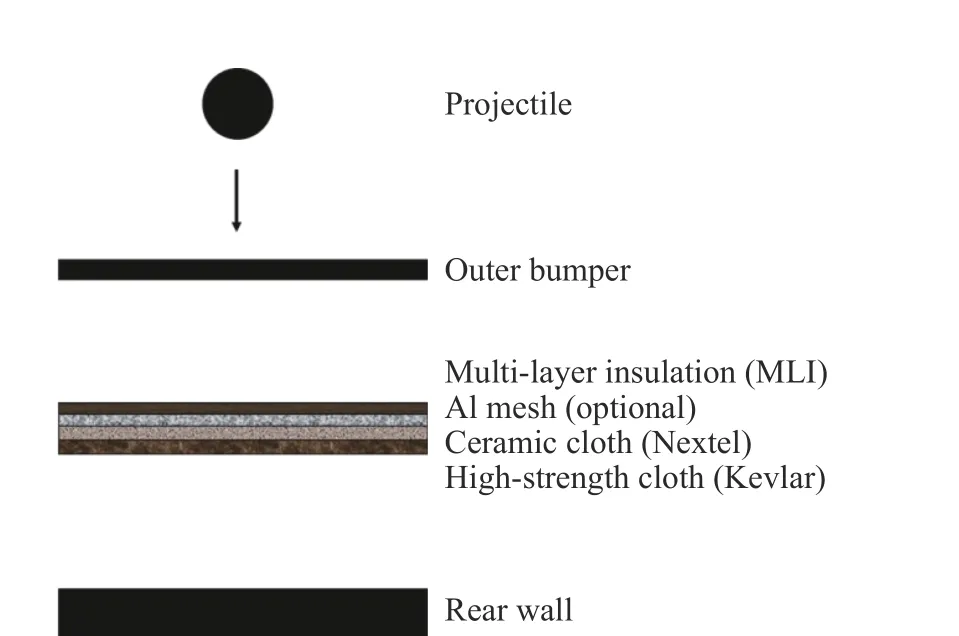
圖5 填充式防護結(jié)構(gòu)[14]Fig. 5 Stuffed Whipple shield[14]
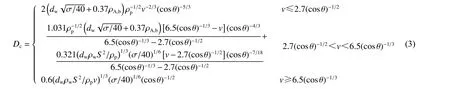
式中:前后板間距S=11.4 cm[14]。
2.1.2 填充式泡沫鋁防護結(jié)構(gòu)
泡沫鋁材料具有吸能效果好且密度較低的優(yōu)勢,應(yīng)用于Whipple 防護結(jié)構(gòu)時可有效地降低結(jié)構(gòu)質(zhì)量。Ryan 等[30]對含開孔泡沫的不同Whipple 防護結(jié)構(gòu)在相同條件下(彈丸直徑D=0.317 5 cm,彈丸速度v=6.8 km/s,入射角θ=0°)的防護性能進行了對比試驗。結(jié)果表明,圖6 所示以泡沫鋁為中間層,鋁薄板為前板的填充式防護結(jié)構(gòu)性能最好。
高速彈丸撞擊填充式泡沫鋁防護結(jié)構(gòu)時,彈丸與前板相互作用,破碎形成碎片云。與傳統(tǒng)Whipple 結(jié)構(gòu)相比,碎片云與中間層接觸前運動的一段距離有利于其膨脹。因此,碎片云在撞擊泡沫鋁中間層時,碎片分布區(qū)域較大,其多孔特性使得碎片在撞擊過程中被多次加載,碎裂更充分,可更有效地分散和吸收碎片云的能量,進一步降低彈丸對航天器的侵徹能力。

圖6 填充式泡沫鋁防護結(jié)構(gòu)[30]Fig. 6 Al-form stuffed Whipple shield[30]
填充式防護結(jié)構(gòu)的中間層與前、后板的間距決定了碎片云與中間層或后板碰撞之前的時間,時間越長,越有利于碎片云的膨脹。前后板間距受到防護結(jié)構(gòu)體積的限制,因此中間層的位置十分重要。賈斌等[31-32]通過改變泡沫鋁填充位置,對泡沫鋁板位于結(jié)構(gòu)中間位置、距前板25%防護結(jié)構(gòu)總長度、距前板75%防護結(jié)構(gòu)總長度和緊貼后板這4 種方案的數(shù)值模擬結(jié)果進行了對比分析,結(jié)果表明,填充位置對于防護結(jié)構(gòu)的性能有較大影響,填充位置在結(jié)構(gòu)中間時性能更優(yōu)[31-32]。
劉文祥等[33]結(jié)合試驗與數(shù)值模擬對泡沫鋁填充式防護結(jié)構(gòu)進行了研究,并與傳統(tǒng)Whipple防護結(jié)構(gòu)進行了對比。試驗結(jié)構(gòu)中前、后板分別為1 和2 mm 厚的鋁板,泡沫鋁板的面密度相當于1 mm 厚鋁板,球形彈丸直徑為2~8 cm,彈速為0.5~7.0 km/s。對比試驗的傳統(tǒng)Whipple防護結(jié)構(gòu)前板厚1 mm,后板厚3 mm。前后板間距S 均為100 mm,總質(zhì)量相同。兩種結(jié)構(gòu)的彈道極限曲線如圖7 所示,填充式泡沫鋁防護結(jié)構(gòu)的彈道極限曲線明顯高于同等面密度和總厚度的傳統(tǒng)Whipple 結(jié)構(gòu),其防護性能更優(yōu)。與傳統(tǒng)Whipple 結(jié)構(gòu)相比,填充式泡沫鋁防護結(jié)構(gòu)總質(zhì)量減少了47%,且能達到與之相同的防護效果[30]。
圖6 所示填充式泡沫鋁防護結(jié)構(gòu)的彈道極限方程[30]可表示為:
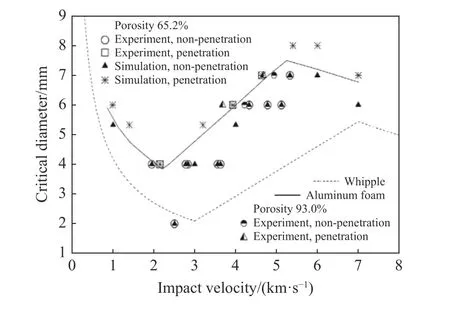
圖7 填充式泡沫鋁防護結(jié)構(gòu)與傳統(tǒng)Whipple 防護結(jié)構(gòu)的彈道極限曲線[33]Fig. 7 Ballistic limit curves of Al-form stuffed Whipple shield and Whipple shield[33]
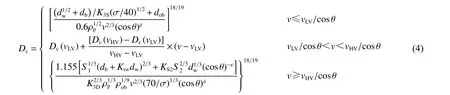
式中:vLV為低速;vHV為高速,vHV=7 km/s;db為防護板厚度;dob為前板厚度;S1為前板到中間層的間距;S2為中間層到后板的間距;K3S、K3D、KS2和Ktw均為經(jīng)驗常數(shù);當θ≤45°或θ≥65°時,δ=4/3,ε=8/3;當45°<θ<65°時,δ=5/4,ε=5/2。vLV的表達式為:
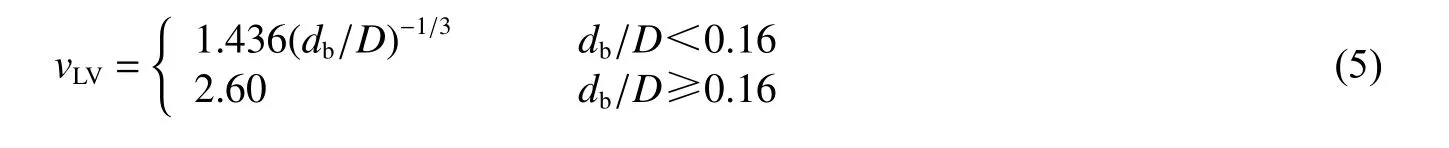
2.2 夾芯板防護結(jié)構(gòu)
夾芯板結(jié)構(gòu)結(jié)合了均質(zhì)金屬板的強度優(yōu)勢和泡沫材料、蜂窩材料的吸能優(yōu)勢,由兩塊均質(zhì)金屬板中間夾一塊泡沫或蜂窩等材料組成。在試驗測試中,金屬蜂窩與金屬泡沫都具有良好的防護性能,可有效地破碎彈丸和減緩碎片速度,同時有助于減少防護結(jié)構(gòu)的總質(zhì)量。將泡沫夾芯板作為前板,與Kevlar 纖維布等材料作為中間層組合成的填充式防護結(jié)構(gòu),也具有優(yōu)異的彈道能力[34]。
2.2.1 蜂窩鋁夾芯板
蜂窩鋁夾芯板是近年來較熱門的一種防護結(jié)構(gòu),蜂窩材料密度低、吸能效果好,能夠提供一定的結(jié)構(gòu)強度且可以兼顧承載能力。為評估蜂窩鋁夾芯板的防護性能,學(xué)者們給出了多種類型的彈道極限方程。Taylor 等[35-36]基于傳統(tǒng)Whipple 防護結(jié)構(gòu)的BLE,修改得出了蜂窩鋁夾芯板的彈道極限方程,但該方程僅適用于部分結(jié)構(gòu)。Ryan 等[37]改進了高速沖擊復(fù)合蜂窩夾芯板的彈道極限方程,在預(yù)測獨立夾芯板結(jié)構(gòu)的彈道性能方面具有較好的準確性。Sibeaud 等[38-39]通過試驗與數(shù)值模擬對比方法改進的彈道極限方程,結(jié)果與試驗更一致。密度為ρp的彈丸以速度vp撞擊蜂窩鋁夾芯板,在低速至高速狀態(tài)下的彈道極限方程均采用以下形式:

彈丸斜撞擊時,蜂窩夾芯起到吸收撞擊能量的主要作用[40],蜂窩鋁夾芯板的防護能力與蜂窩夾芯的特殊結(jié)構(gòu)有著密不可分的關(guān)系。超高速撞擊時,夾芯內(nèi)蜂窩細胞的細胞壁使得碎片云分離成幾部分,限制了碎片云的徑向膨脹[1,16, 39,41-43]。如圖8 所示,以直徑7 mm、速度5.82 km/s 的鋁球撞擊蜂窩鋁夾芯板,2.0 μs 時可明顯觀察到絕大部分碎片云沿著蜂窩孔橫向運動[41]。這也導(dǎo)致碎片云將以一個較高的速度對后板進行沖擊,試驗估計撞擊后板時的速度為4.83 km/s。這種現(xiàn)象被稱為溝道效應(yīng),最早在Anon[44]的研究中被提出。隨后的研究指出,在超高速撞擊情況下,蜂窩結(jié)構(gòu)的溝道效應(yīng)將降低蜂窩鋁夾芯板的防護能力[45],并受到結(jié)構(gòu)前后板間距、蜂窩細胞直徑、蜂窩夾芯的尺寸和深度的影響[46]。
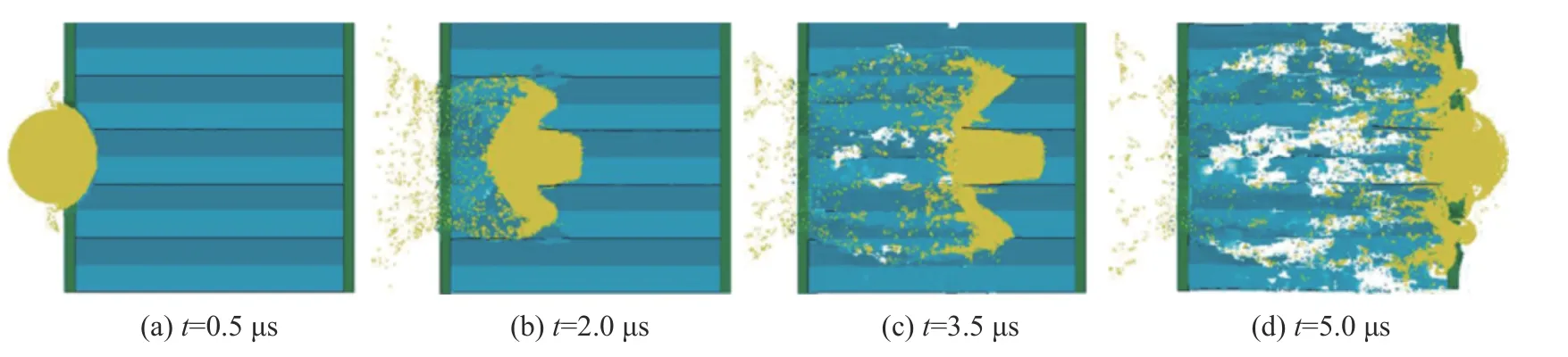
圖8 彈丸高速撞擊蜂窩鋁夾芯板的破碎過程[41]Fig. 8 Simulation of hypervelocity impacts on honeycomb sandwich structure[41]
目前多數(shù)研究表明溝道效應(yīng)在彈丸正撞擊時表現(xiàn)更明顯,斜撞擊時蜂窩的胞壁結(jié)構(gòu)能更好地吸收碎片云的動量,從而減小其對后板的沖擊。圖9 為入射角 θ分別為0°、30°、45°時蜂窩鋁夾芯板防護結(jié)構(gòu)的彈道極限曲線,同等撞擊速度下,彈丸入射角度越大,彈丸臨界直徑越高。Kang 等[47]在研究中對不同的蜂窩孔單元尺寸、孔壁厚度、蜂窩夾芯深度進行了模擬,固定其他無關(guān)參數(shù),指出當蜂窩孔尺寸減小時,徑向通道的寬度變短,同一區(qū)域的胞壁結(jié)構(gòu)更多,從而增加碎片云與胞壁的碰撞,能進一步降低碎片云的速度。當溝道效應(yīng)存在時,蜂窩孔單元尺寸是影響臨界彈丸直徑的主要因素,蜂窩夾芯板的BLE方程可通過蜂窩孔單元尺寸的歸一化函數(shù)來修正。
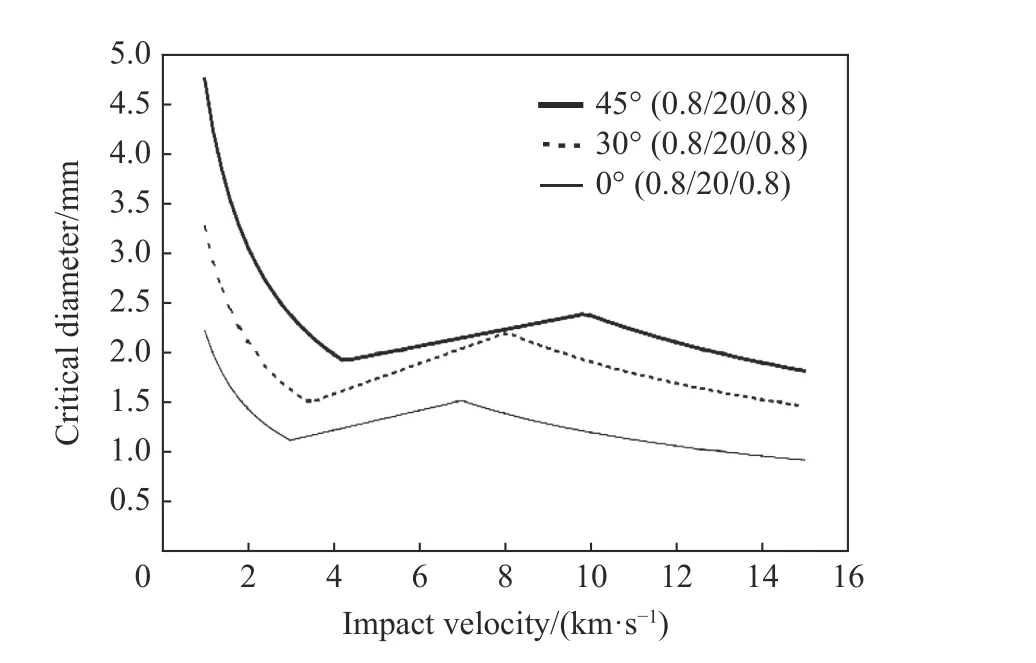
圖9 不同入射角度蜂窩鋁夾芯板防護結(jié)構(gòu)的彈道極限曲線[39]Fig. 9 Projectile critical perforation diameter as a function of impact velocity against the same honeycomb panel[39]
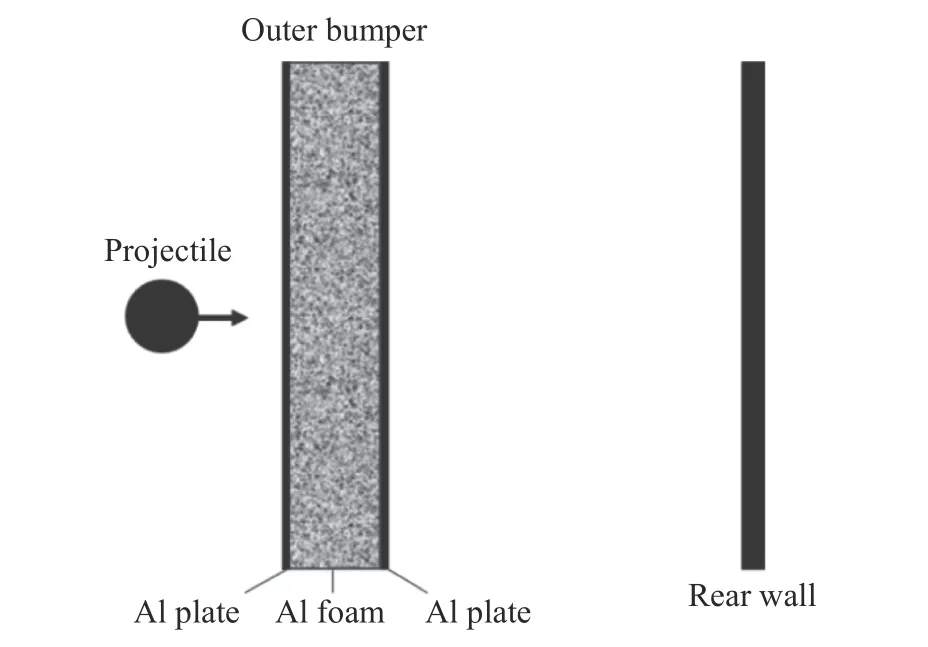
圖10 泡沫鋁夾芯板防護結(jié)構(gòu)示意圖[32]Fig. 10 Schematic configuration of Al-foam sandwiched shield[32]
2.2.2 泡沫鋁夾芯板
與蜂窩材料規(guī)則的孔隙結(jié)構(gòu)不同,泡沫材料的密度更大,其孔隙形狀和大小具有隨機性。2003 年,Destefanis 等[15]對多種材料的靶板進行了輕氣炮沖擊試驗,其中包括泡沫鋁、陶瓷、芳族聚酰胺織物、聚氨酯泡沫、鈦鋁合金等。試驗證明,泡沫鋁夾芯結(jié)構(gòu)在2.4~6.5 km/s 的測試速度范圍內(nèi)可對彈丸進行多次沖擊。夾層板的首層鋁板可使彈丸迅速破碎,首層鋁板失效后,剩余彈丸及形成的碎片與泡沫鋁夾芯碰撞,進一步破碎并降低沖擊速度,泡沫的多孔結(jié)構(gòu)能夠吸收碎片云的部分能量,第3 層鋁板使得碎片更小、更分散。圖10 所示為基于鋁板與泡沫鋁夾芯板的防護結(jié)構(gòu),具有良好的彈道性能和結(jié)構(gòu)性能。
有關(guān)數(shù)值模擬研究[32,48]結(jié)果均表明:低于某一確定速度界限時,泡沫鋁夾芯板的防護性能優(yōu)于傳統(tǒng)Whipple 結(jié)構(gòu)和填充式泡沫鋁防護結(jié)構(gòu);高于速度界限時,填充式泡沫鋁防護結(jié)構(gòu)的防護性能更優(yōu)。速度界限受到材料、結(jié)構(gòu)等不同因素的影響。
同為常用的夾芯板材料,泡沫和蜂窩材料防護性能的差異值得探討。直徑為3.6 mm 的鋁球以(6.49±0.27)km/s 的速度撞擊5.08 cm 厚夾芯板的損傷對比如圖11 所示[49-50],等密度下蜂窩夾芯板的面板厚度大于泡沫夾芯板(分別為0.127 0 和0.025 4 cm)。由蜂窩夾芯的損傷區(qū)域可明顯觀察到溝道效應(yīng)的影響,而泡沫夾芯的均勻性使得碎片云在各個方向的擴展阻力相等。夾芯板后面板的損傷結(jié)果表明,高速撞擊時泡沫夾芯比蜂窩夾芯的防護潛力更高。

圖11 開孔泡沫夾芯板和蜂窩夾芯板損傷對比[50]Fig. 11 Comparison of damages in open-cell foam core and honeycomb core sandwiches[50]
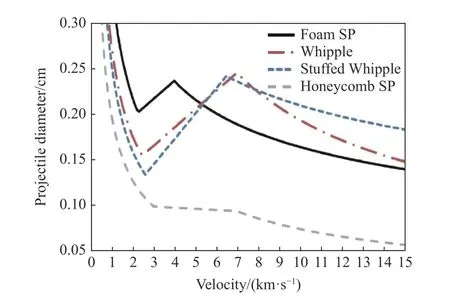
圖12 等質(zhì)量的不同Whipple 防護結(jié)構(gòu)彈道極限曲線對比[48]Fig. 12 Comparison of ballistic limit curves for comparable weight/standoff Whipple shield types[48]
Ryan 等[48]對等質(zhì)量的泡沫鋁結(jié)構(gòu)、傳統(tǒng)Whipple 防護結(jié)構(gòu)、蜂窩鋁結(jié)構(gòu)、填充式防護結(jié)構(gòu)進行了對比,給出了4 種防護結(jié)構(gòu)的彈道極限曲線,如圖12 所示。在0~15 km/s 速度范圍內(nèi),泡沫鋁夾芯板的性能明顯優(yōu)于蜂窩夾芯板。超高速碰撞下,蜂窩結(jié)構(gòu)的彈道極限曲線并不符合一般Whipple 結(jié)構(gòu)的“三段式”規(guī)律,其防護能力隨撞擊速度的增大而持續(xù)降低直至基本失效。填充式防護結(jié)構(gòu)與泡沫鋁夾芯板結(jié)構(gòu)的防護性能較為穩(wěn)定優(yōu)異。
泡沫結(jié)構(gòu)的防護性能較蜂窩結(jié)構(gòu)更優(yōu)[50-51],泡沫夾芯板具有良好的輕質(zhì)強度和剛度性能。根據(jù)內(nèi)部孔隙是否相連,泡沫材料可分為開孔泡沫和閉孔泡沫兩大類,相較于閉孔泡沫,開孔泡沫質(zhì)量較輕,均質(zhì)性更好。開孔泡沫結(jié)構(gòu)復(fù)雜,一般通過基材相對密度(百分比)和孔隙密度(單位英寸長度上的平均孔數(shù),單位:PPI)來定義,孔隙密度不同,開孔泡沫的胞孔結(jié)構(gòu)(圖13)也存在一定差異。孔隙密度的改變可對泡沫結(jié)構(gòu)防護性能產(chǎn)生一定影響。
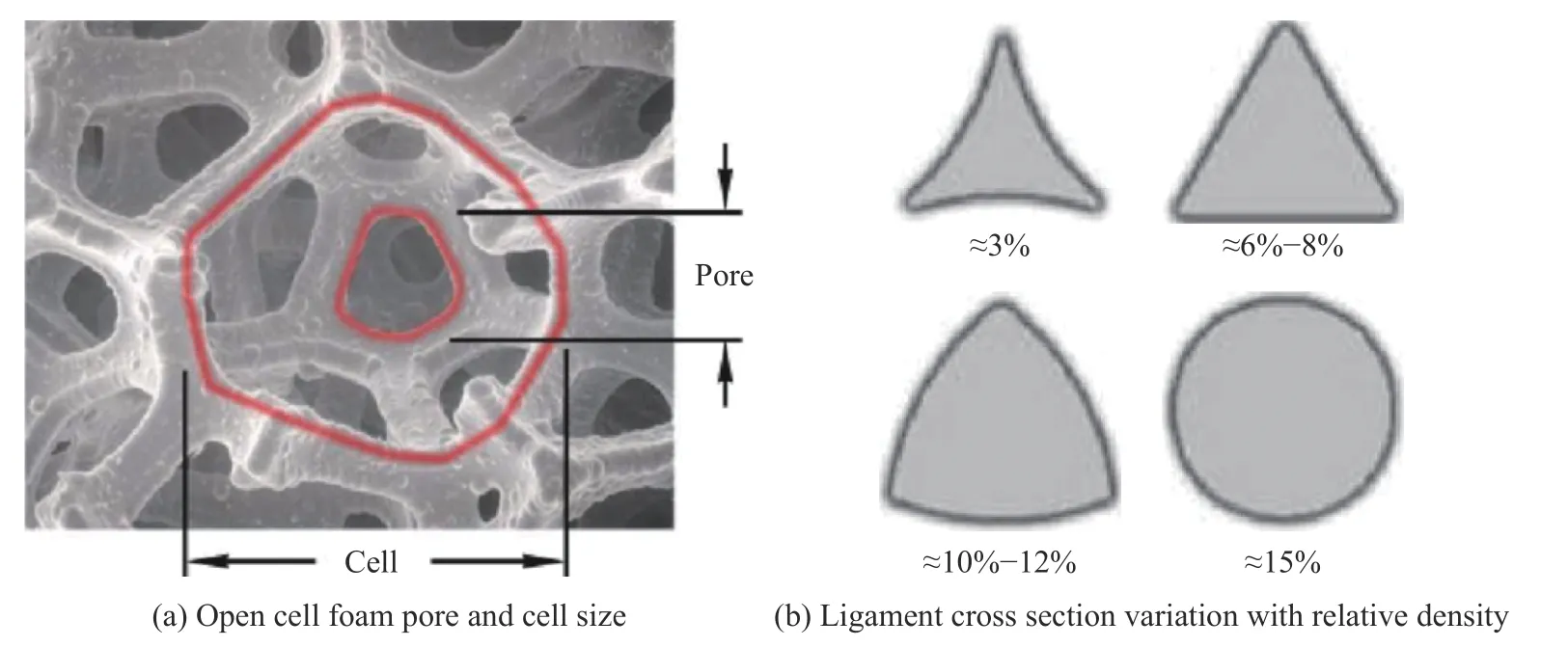
圖13 開孔泡沫孔隙與泡沫孔大小和不同孔隙率的孔隙形狀示意圖[48]Fig. 13 Open cell foam pore and cell size and ligament cross section variation with relative density[48]
Ryan 等[50]測試了10、20、40 PPI 這3 種不同孔隙密度的泡沫鋁材料,發(fā)現(xiàn)隨著孔隙密度的增大,防護性能有所提高,但提升幅度很小,說明孔隙密度對防護性能的影響有限。劉文祥等[33]對孔隙率為65.2%和93.0%的兩種泡沫鋁防護板進行了對比研究,Gaitanaros 等[52]通過改變開孔泡沫的相對密度(3.67%~10.00%)來研究其影響,同樣證明了這一點。對于純鋁泡沫,孔隙率的影響較小,若改變金屬泡沫的材料成分,孔隙密度對防護性能的影響如何變化還有待研究。
胞孔結(jié)構(gòu)的規(guī)則性決定著泡沫的拓撲結(jié)構(gòu),從而影響泡沫金屬材料的機械性能。Shi 等[53]認為胞孔的不規(guī)則性僅影響彈性范圍內(nèi)的細胞邊緣彎曲行為,對彈性模量影響不明顯,但規(guī)則性低的泡沫受加載速度影響較小,適用于防護結(jié)構(gòu)。
2.2.3 雙層夾芯板結(jié)構(gòu)
兩種雙層夾芯板的結(jié)構(gòu)如圖14 所示[49-50],其總面密度分別為DL-H(double-layer honeycomb,DL-H):1.57 g/cm2,DL-F(double-layer foam,DL-F):1.68 g/cm2。為平衡兩種結(jié)構(gòu)的總面密度,泡沫結(jié)構(gòu)的第2 層防護板沒有添加鋁面板。雙層夾芯板結(jié)構(gòu)在前板前端附加如圖14 所示的第1、2 層鋁網(wǎng),外層鋁網(wǎng)的存在使得彈體在撞擊前面板之前已被破壞,確保了在泡沫芯內(nèi)傳播的碎片更小。
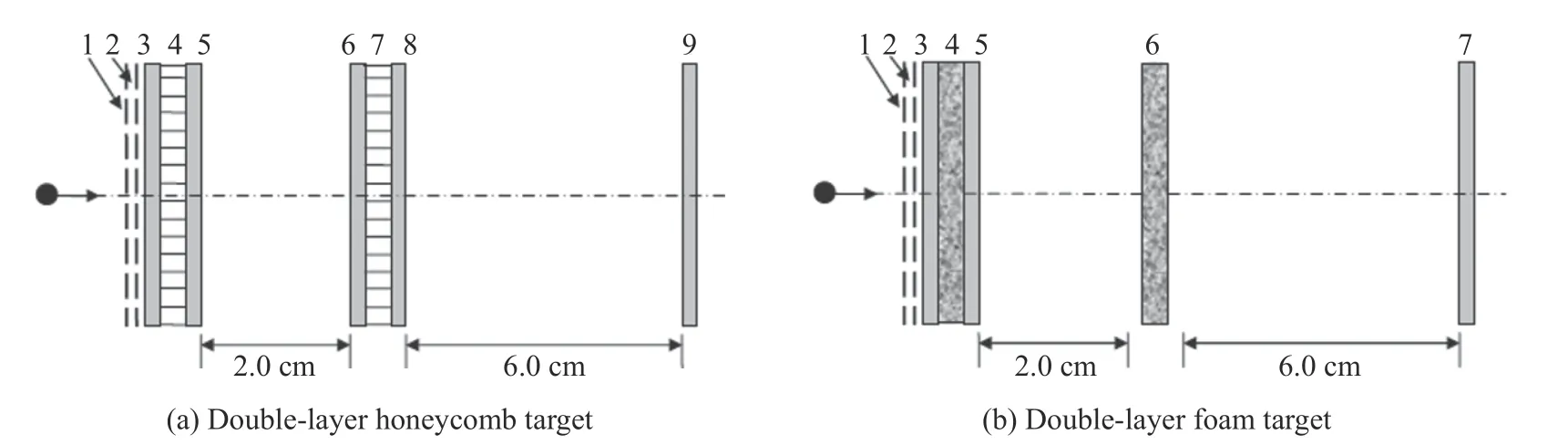
圖14 雙層蜂窩結(jié)構(gòu)(DL-H) 和雙層泡沫結(jié)構(gòu)(DL-F) [16]Fig. 14 Schematic of the double-layer honeycomb target and the double-layer foam target [16]
當蜂窩鋁或泡沫鋁作為Whipple 結(jié)構(gòu)的填充材料時,能夠更有效地保護航天器,使其免受超高速粒子的碰撞損傷。相較于傳統(tǒng)的雙層板結(jié)構(gòu),在垂直入射時,雙層泡沫結(jié)構(gòu)在低速(3 km/s)下使臨界彈丸直徑提高了15%,在高速(7 km/s)時提高了3%。隨著彈丸撞擊的傾斜度增加,彈丸與泡沫芯的接觸面積擴大,破碎程度增加,在60°時臨界彈丸直徑提高29%。但雙層蜂窩結(jié)構(gòu)的防護性能提升并不明顯。試驗結(jié)果顯示,撞擊速度為5.6 km/s 時,雙層泡沫結(jié)構(gòu)可使碎片破碎和熔化的比例增加,優(yōu)于雙層蜂窩結(jié)構(gòu)。
Ryan 等[16]根據(jù)試驗結(jié)果對Sanchez[54]提出的彈道極限方程作出修正,得到兩種結(jié)構(gòu)的彈道極限方程,分別表示為:
雙層蜂窩結(jié)構(gòu)(DL-H)

2.3 小結(jié)
Whipple 防護結(jié)構(gòu)發(fā)展至今,填充式結(jié)構(gòu)與夾芯板結(jié)構(gòu)的防護性能較為穩(wěn)定優(yōu)異,滿足質(zhì)量強度標準,應(yīng)用較廣。夾芯板結(jié)構(gòu)常用的夾芯材料主要包括金屬泡沫、金屬蜂窩等。這些材料在某種程度上對碎片的加載更充分,可減緩粒子速度,并減少結(jié)構(gòu)總質(zhì)量。其中,蜂窩材料密度更低,但溝道效應(yīng)使得其無法滿足更高速度正撞擊的防護強度要求,因此金屬泡沫的應(yīng)用潛力更大。
超高速撞擊下的Whipple 防護結(jié)構(gòu),由于試驗成本高昂,需要將試驗與數(shù)值模擬相結(jié)合進行對比論證,最后確定研究和發(fā)展方向。泡沫材料具有復(fù)雜的內(nèi)部結(jié)構(gòu),其力學(xué)性能與孔隙結(jié)構(gòu)息息相關(guān)。為更好地開展泡沫材料的研究,建立細觀模型顯得尤為必要。但常用的光滑粒子流體動力學(xué)(smoothed particle hydrodynamics,SPH)方法與有限元方法在研究超高速碰撞問題時均有一定缺陷,進行復(fù)雜結(jié)構(gòu)材料的數(shù)值模擬研究時,更面臨著建模困難、計算量較大、計算不穩(wěn)定等問題。如何對數(shù)值模擬方法進行改進,使其能夠適用于復(fù)雜結(jié)構(gòu)的超高速碰撞研究,找到更加適合的研究方案值得探討。
3 數(shù)值模擬方法
防護結(jié)構(gòu)發(fā)展過程中,常用的研究方法為試驗和數(shù)值模擬。將數(shù)值模擬方法、材料模型和詳細的防護結(jié)構(gòu)設(shè)計試驗研究相結(jié)合[55],對于促進航天器防護結(jié)構(gòu)的發(fā)展十分有利。當沖擊速度在7 km/s 以上時,試驗要求更高,數(shù)據(jù)采集難度更大。可先通過數(shù)值模擬方法來確定更優(yōu)的試驗方案和材料選取,再進行試驗驗證,以此提高研究效率。
超高速碰撞的主要特點是高應(yīng)變率帶來材料的大變形、斷裂以及破壞失效。利用數(shù)值模擬方法研究超高速碰撞時,有限元常受限于大變形下的單元畸變、單元失效刪除帶來的能量損失等問題,難以給出好的計算結(jié)果。因此,無網(wǎng)格的SPH 方法在超高速碰撞領(lǐng)域得到廣泛應(yīng)用。數(shù)值模擬中常用無網(wǎng)格法及其與有限元的耦合算法,張雄等[56-57]和胡德安等[58]分別對其研究進展進行了詳細論述。本文中主要針對Whipple 結(jié)構(gòu)在超高速碰撞下產(chǎn)生碎片云及復(fù)雜結(jié)構(gòu)的破壞問題,總結(jié)分析相應(yīng)的數(shù)值模擬方法及其改進方向。
3.1 SPH 方法
SPH 方法最早提出于1977 年,用于模擬天體物理現(xiàn)象[59-60]。1990 年,Libersky 等[61]首次提出可將SPH 方法應(yīng)用于高速碰撞領(lǐng)域,隨后Libersky 等[62-63]、Randles 等[64]通過引入材料強度并針對SPH 方法在邊界條件和連續(xù)性方面的缺陷進行改進,模擬了高速碰撞問題中的斷裂和破碎現(xiàn)象。
SPH 方法的主要思想是通過使用一系列任意分布的節(jié)點或粒子來求解問題,可得到精確穩(wěn)定的數(shù)值解。這些節(jié)點或粒子之間不需要單元進行連接,可有效避免單元畸變、單元失效刪除帶來的能量損失等問題。SPH 方法能準確描述材料在經(jīng)歷較大變形時的現(xiàn)象,在解決超高速撞擊問題[30,61-66]和高速侵徹問題[67]方面均有好的表現(xiàn)。但SPH 方法在復(fù)雜結(jié)構(gòu)的建模上有一定困難,研究超高速碰撞問題時,對泡沫、蜂窩、編織等材料,難以進行細觀建模。計算過程中,細觀模型復(fù)雜結(jié)構(gòu)的不規(guī)則性使得粒子的分布受到影響,難以保持計算穩(wěn)定。
計算不穩(wěn)定的問題,主要體現(xiàn)在拉伸狀態(tài)下的應(yīng)力不穩(wěn)定[68-70]、計算中的數(shù)值不穩(wěn)定[71-72]等方面。SPH 方法的物質(zhì)邊界不明確,物理邊界施加困難。其中,物質(zhì)邊界不明確是SPH 方法目前無法避免的問題,SPH 方法中的粒子僅有一個節(jié)點,無法記錄形狀信息。建立在一系列離散點上的近似函數(shù)較復(fù)雜,且計算量較大,計算效率低于有限元方法。在研究超高速碰撞問題時,只基于SPH 粒子的計算結(jié)果無法獲得所需碎片的準確形狀、尺寸等參數(shù),因此,需要對SPH 方法進行改進,以期獲得碰撞后的碎片形狀、分布、溫度等信息。
3.1.1 計算穩(wěn)定性
SPH 方法的計算穩(wěn)定性受到SPH 粒子分布的影響。初始粒子的分布較為重要,在粒子分布較為規(guī)則和均勻時,其計算結(jié)果與解析解更吻合,故SPH 計算應(yīng)采用盡可能規(guī)則和連續(xù)性較好的初始粒子,以提高計算精度和保證計算穩(wěn)定性[73]。
SPH 粒子生成目前可通過兩種常用方法來實現(xiàn)。第一種方法是將特定模型進行均勻的區(qū)域劃分,一般有矩形粒子分布[74]、圓形粒子分布[75-76]等,粒子可直接在區(qū)域內(nèi)生成。但對于結(jié)構(gòu)較復(fù)雜的模型,粒子的均勻分布很難達成,劃分方式困難且計算量龐大。第二種方法則為粒子的單元轉(zhuǎn)化法,即通過單元劃分,在單元中心處生成SPH 粒子,初始粒子的均勻性只能通過單元的均勻性來實現(xiàn),該方法對單元劃分要求較高。
倪國喜等[75]給出了任意區(qū)域的粒子均勻分布方法。首先,在給定的計算區(qū)域邊界生成逆時針排序且均勻分布的邊界點,將相鄰兩個邊界點連線向區(qū)域內(nèi)部作正三角形,在三角形外心出生成邊界粒子。再采用Delaunay 三角劃分方法,以邊界粒子為基礎(chǔ)生成Delaunay 三角。其次,令Delaunay 三角的頂點為內(nèi)粒子,外心為Voronoi 頂點,將其逆時針連接起來即可得到Voronoi 多邊形。邊界上將Delaunay 三角的外心與相鄰邊粒子連線的中垂線于區(qū)域邊界的交點逆時針順序連接。最后,計算Voronoi 面積和體積,則可以得到均勻分布的初始粒子。
傳統(tǒng)的SPH 方法中,初始的粒子分布會隨著計算過程的推進而逐漸失去規(guī)則性,難以保持數(shù)值穩(wěn)定,并且存在拉伸狀態(tài)下的應(yīng)力不穩(wěn)定問題。目前可成功改善SPH 方法拉伸不穩(wěn)定的方法主要有應(yīng)力點法[69,77]和人工應(yīng)力法[78]等,還有部分學(xué)者通過對核函數(shù)、光滑性等的修正來消除拉伸不穩(wěn)定性。
Liu 等[79-80]對SPH 方法的平滑函數(shù)進行了改進,使用一組基函數(shù)來代替平滑函數(shù)及其導(dǎo)數(shù),稱為有限質(zhì)點法(finite particle method,F(xiàn)PM)。FPM 方法應(yīng)用在不可壓縮流體問題中,可確保粒子近似方案的一階連續(xù)性。對函數(shù)及其各方向?qū)?shù)的核近似和粒子近似采取耦合聯(lián)立求解的方式[81],可提高計算精度和穩(wěn)定性。
Swegle 等[70]認為可通過構(gòu)造在拉伸狀態(tài)下穩(wěn)定的核函數(shù)來提高穩(wěn)定性,提出傳統(tǒng)SPH 方法應(yīng)力不穩(wěn)定的充分條件為:

式中:W 為核函數(shù);T 為應(yīng)力,壓縮狀態(tài)為負,拉伸狀態(tài)為正。
基于穩(wěn)定性條件,楊秀峰等[82]對核函數(shù)進行了調(diào)整,使其滿足在壓縮狀態(tài)下,令排斥力隨著粒子間距的減小而增大;在拉伸狀態(tài)下,令吸引力隨著粒子間距的減小而減小,或者通過某種方式將吸引力轉(zhuǎn)化成排斥力,并令排斥力隨著粒子間距的減小而增大,從而避免粒子相互靠近的思想來滿足穩(wěn)定性條件。對于流體問題,可通過構(gòu)造二階導(dǎo)數(shù)非負的核函數(shù)來消除壓縮不穩(wěn)定性,改進離散格式使得到的粒子間作用力恒為排斥力,以此來消除拉伸不穩(wěn)定性。這種穩(wěn)定的SPH 方法(stabilized SPH,SSPH)在理論上具有普適性,對于改進SPH 方法的應(yīng)力不穩(wěn)定問題具有一定意義。
3.1.2 碎片識別
超高速撞擊產(chǎn)生的碎片云顆粒在形狀、大小、速度分布上有一定的差異[83-84],由于碰撞時間極短,難以通過試驗獲得單個碎片的信息。因此,需要通過數(shù)值模擬方法識別碎片云團中質(zhì)量尺寸較大、侵徹能力較強的危險碎片,確定其分布特性。傳統(tǒng)SPH 方法研究超高速碰撞問題時,所得碎片云由離散粒子組成,其邊界模糊,單個碎片和裂紋與未裂紋材料界面的識別較為困難,無法對碎片形態(tài)和數(shù)量等信息進行準確描述。
為解決碎片識別問題,Hockney 等[85-86]提出使用鏈表法(linked lists)搜索相鄰的SPH 粒子,以此來確定斷裂和破碎的具體形態(tài),但其具有很大的局限性,隨后被更有效的層次樹法(hierarchical tree methods)替代[87]。Benz 等[88-89]、徐金中等[90]提出了一種基于鏈表的搜索算法,通過秩來儲存每個單元在3 個軸上的實際空間范圍,獲得秩空間與實際空間的映射,在秩空間構(gòu)造鏈表。由任一未損壞粒子開始搜索距其一個單位長度內(nèi)的鄰近粒子,直到此區(qū)域不存在未損壞粒子,可識別碎片。Liang 等[91]以廣度優(yōu)先搜索(breadth first search,BFS)算法來確定同一連通域內(nèi)的點集,通過定義閾值參數(shù)l0(略大于碰撞前兩個粒子的初始距離)來判斷相鄰粒子是否屬于同一碎片,所得結(jié)果中大尺寸碎片的數(shù)量與試驗結(jié)果一致。這些研究均基于某一特定時刻的粒子位置來確定碎片,因此在計算成本和準確性方面存在一定的局限性。
超高速碰撞過程中SPH 粒子的流動范圍較大,無法確定相鄰粒子是否均屬于同一碎片。在碰撞的極短時間內(nèi),可認為碎片在空間中分散時以勻速沿直線軌跡運動,在相同時間間隔內(nèi),其位移為一恒定值,同一碎片中的粒子與碎片的直線軌跡幾乎相同。Sakong 等[92]據(jù)此提出可通過k-means 算法將軌跡相似的粒子分類并聚集到同一碎片中,提高碎片與粒子相對應(yīng)的準確率,可通過每個碎片的粒子計算出其質(zhì)量、速度和動能等信息,定量評估不同碎片對Whipple 結(jié)構(gòu)的威脅程度,試驗驗證其有效性。
Zhang 等[93-96]結(jié)合SPH 方法與有限元方法,提出了有限元重構(gòu)法(finite element reconstruction,F(xiàn)ER),使用連續(xù)形式的核近似和粒子近似格式,先通過有限元方法在每個單元的形心處生成一個SPH 粒子,建立SPH 粒子-形心重合模型[94],再通過SPH 方法進行仿真求解,最后進行有限元重構(gòu)。利用SPH 粒子的坐標向量插值,重建立方體單元的節(jié)點坐標向量[95]。將應(yīng)力作用下產(chǎn)生斷裂和相變的重建立方體單元認定為失效單元并刪除,以其對應(yīng)的SPH 粒子作為替代。可根據(jù)粒子和單元來區(qū)分單元的失效狀態(tài),并利用有限元單元的連通性進行碎片識別[95]。如圖15 所示,F(xiàn)ER 方法在碎片識別方面比SPH 方法具有一定優(yōu)勢,能夠給出清晰的危險碎片形態(tài)及其質(zhì)量、大小和速度矢量等信息,也可提供碎片總數(shù)、碎片云結(jié)構(gòu)和物體的破碎過程,但其計算過程過于復(fù)雜。
針對SPH 方法的固有缺陷,已有許多研究人員對其計算不穩(wěn)定、碎片識別和邊界問題進行了改進,并成功應(yīng)用于超高速撞擊模擬研究。但計算結(jié)果并不完美,且復(fù)雜結(jié)構(gòu)的建模與計算困難、計算效率低、物質(zhì)邊界不明確等問題仍然存在。研究泡沫、蜂窩、編織等材料及其細觀模型時,僅僅使用SPH 方法無法給出好的計算結(jié)果,因此需要將SPH 方法與有限元方法相結(jié)合進行計算。
3.2 有限元方法與SPH 方法的耦合計算
有限元方法與SPH 方法均在數(shù)值模擬中被廣泛應(yīng)用,分別在研究固體力學(xué)與流體力學(xué)時有較好的表現(xiàn)。SPH 方法難以處理復(fù)雜結(jié)構(gòu)的建模計算、碎片識別等問題,而有限元方法無法處理大變形條件下單元畸變刪除帶來的能量損失和計算不穩(wěn)定問題。有限元方法與SPH 方法的耦合計算可有效地改善以上缺陷,并已成功應(yīng)用于超高速碰撞研究。胡德安等[58]將有限元方法與SPH 方法的耦合算法分為固定耦合算法[97-100]和自適應(yīng)耦合算法[99,101]兩大類,主要區(qū)別在于是否在初始時刻即固定有限元與SPH 粒子的計算區(qū)域。
3.2.1 固定耦合算法
SPH 方法在計算復(fù)雜模型時,存在計算效率過低的問題。固定耦合算法綜合了有限元法在小變形區(qū)域計算效率高、SPH 方法在大變形區(qū)域可有效避免單元畸變的優(yōu)點,在計算初始時刻,根據(jù)計算需求對模型進行區(qū)域劃分,固定有限元方法與SPH 方法的計算區(qū)域,在后續(xù)計算過程中保持不變。
部分學(xué)者應(yīng)用固定耦合算法模擬超高速彈丸侵徹金屬靶板過程,將板中彈丸的直接作用區(qū)域用SPH 粒子進行劃分,靶板其余部分采用有限元單元進行劃分。研究彈丸變形較小的高速撞擊問題時常將彈丸用有限元單元劃分,采取將SPH 節(jié)點定義為從節(jié)點,與之接觸的界面單元表面定義為主表面的方法來定義耦合界面的接觸[100,102]。研究超高速碰撞形成碎片云的問題時將彈丸用SPH 粒子劃分,取單元表面的一個節(jié)點為從節(jié)點,通過接觸算法定義從節(jié)點與主表面在耦合界面的相互作用。與純SPH 方法的數(shù)值模擬結(jié)果進行對比,兩種方法所得的碎片云形態(tài)幾乎沒有差異,通過此方法可較好地模擬超高速碰撞的穿孔特性[103-106]。
固定耦合算法可成功模擬超高速碰撞問題,相較于純SPH 方法,可在保證計算精度的同時,大大減少計算時間,提升計算效率,但固定耦合算法建模較復(fù)雜,且并不能解決SPH 方法固有的拉伸不穩(wěn)定以及計算精度等問題。
3.2.2 FEM-SPH 自適應(yīng)耦合算法
自適應(yīng)耦合算法與固定耦合算法的最大區(qū)別,是自適應(yīng)耦合算法在計算過程中將單元自動轉(zhuǎn)換成SPH 粒子[99,107-110]。1994 年,Johnson 等[99]提出了根據(jù)等效塑性應(yīng)變將單元轉(zhuǎn)換成粒子的思想,單元與SPH 粒子使用相同的材料模型,并通過與SPH 粒子固結(jié)的有限元節(jié)點傳遞二者之間的相互作用力。通過設(shè)定一定的等效塑性應(yīng)變作為單元失效判據(jù),在達到失效條件時,用SPH 粒子同時替換單元的質(zhì)量與體積,但其在計算應(yīng)變率時忽略了相鄰節(jié)點的影響,無法保證耦合界面處物理量的連續(xù)性。后續(xù)Johnson 等對此方法進行了改進,提出了自適應(yīng)耦合算法,應(yīng)用匹配算法來解決耦合界面問題。但是該方法受到拉伸不穩(wěn)定性的限制。
Beissel 等[111-112]在此基礎(chǔ)上繼續(xù)改進,對超高速下球形彈丸、柱形彈丸以及圓盤形彈丸與薄板正撞擊產(chǎn)生的碎片云進行了模擬,還模擬了圓盤形彈丸以20.6°傾角與薄板超高速撞擊產(chǎn)生的碎片云,并與試驗結(jié)果進行了對比。以球形彈丸為例,初始彈體結(jié)構(gòu)被均勻劃分為拉格朗日單元,將SPH 粒子的轉(zhuǎn)化條件設(shè)置為拉格朗日單元達到塑性應(yīng)變失效。在彈體碰撞破碎的過程中,不斷發(fā)生SPH 粒子的轉(zhuǎn)化。圖16 為5 種不同沖擊速度下的彈丸損傷示意圖,藍色到紅色的轉(zhuǎn)變代表損傷程度加深,紅色部分表示已完成單元到粒子的轉(zhuǎn)化。模擬結(jié)果可大致給出與試驗相符的碎片云形態(tài)及形成特征,碎片云主體較清晰,計算效率有所提升。但是,由圖16 可明顯觀察到粒子過于分散,可能存在粒子穿透單元的問題,且計算結(jié)果中穿孔形狀與實際孔的形狀有所不同,因此該算法仍需改進。
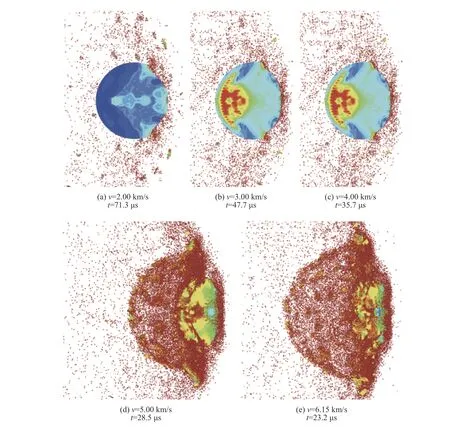
圖16 5 種不同沖擊速度下球形彈體的損傷對比[111]Fig. 16 Damage in aluminum spheres due to impact with aluminum bumpers at five different velocities[111]
2015 年,Johnson 等[113]繼續(xù)完善之前的工作并提出了組合粒子元法(combined particle-element method,CPEM),該方法初始為四面體或六面體單元模型,將原始單元的積分點轉(zhuǎn)換為無質(zhì)量的應(yīng)力點,將質(zhì)量和應(yīng)力施加到單元節(jié)點上。使用有限元算法計算粒子節(jié)點的承受力,當其等效塑性應(yīng)變超過指定值(εerit)時,單元自動轉(zhuǎn)換為SPH 粒子。其優(yōu)勢在于可使用有限元計算低應(yīng)變單元(應(yīng)力點),無網(wǎng)格法計算轉(zhuǎn)換后的高應(yīng)變率SPH 粒子,計算結(jié)果精度較高。
Johnson 等[107,114]采用廣義粒子算法(generalized particle algorithm,GPA)將單元轉(zhuǎn)換成SPH 粒子,提出了一種新的接觸滑動界面算法,對所有的粒子表面節(jié)點設(shè)置一個虛擬直徑DS,當一些表面單元被轉(zhuǎn)化時,粒子與單元表面的接觸將過渡為粒子與粒子的接觸[115]。當只有一種材料發(fā)生粒子轉(zhuǎn)換時,該算法具有優(yōu)異的計算效率和精度,但當轉(zhuǎn)換材料為兩種及以上時,可能存在部分較小粒子穿過轉(zhuǎn)化界面的問題。
此外,國內(nèi)外許多研究者也應(yīng)用自適應(yīng)耦合算法開展了超高速碰撞相關(guān)問題的研究。2000 年,Sauer 等[116]提出了基于四邊形單元和六面體單元的自適應(yīng)耦合算法,王吉等[117]在此基礎(chǔ)上對Taylor 碰撞、超高速彈丸侵徹半無限厚靶等問題進行了模擬,計算效率得到較大提高。張志春等[118]以等效應(yīng)力作為單元轉(zhuǎn)化準則,根據(jù)FEM-SPH 耦合算法,在有限元節(jié)點設(shè)置背景粒子,對高速沖擊問題進行了研究,使得有限元節(jié)點可被鄰近的SPH 粒子搜索到,以此保證耦合界面物理量及核函數(shù)的連續(xù)性,消除邊界效應(yīng)。肖毅華等[101]提出了自適應(yīng)軸對稱FEM-SPH 耦合算法對彈體侵徹鋁板和混凝土板進行模擬。Deconincka 等[41]將自適應(yīng)耦合算法應(yīng)用在超高速彈丸撞擊蜂窩板的模擬中,其中拉格朗日單元采用彈塑性本構(gòu)方程,SPH 粒子采用彈塑性流體動力學(xué)法及Mie-Grüneisen 狀態(tài)方程定義,所得結(jié)果與試驗相符。
He 等[119]對單元失效判據(jù)進行優(yōu)化,采用FEM-SPH 自適應(yīng)耦合算法對碎片云問題進行數(shù)值模擬,取得了較好結(jié)果。對FEM-SPH 自適應(yīng)耦合算法提出了3 種不同的實現(xiàn)形式,選取了其中計算效果最好的方案。以Piekutowski[120-121]開展的撞擊速度分別為2.54 和6.71 km/s 的兩個試驗工況為例進行計算,采用Lagrange 單元對模型建模,并在單元中加入粒子化算法的關(guān)鍵字。在計算中,使用自適應(yīng)算法令SPH 粒子代替滿足失效判據(jù)而刪除的單元繼續(xù)計算。特別地,單元失效判據(jù)同時采用Johnson-Cook 失效判據(jù)和最大拉應(yīng)力失效判據(jù),較好地反應(yīng)了材料的實際破壞行為。模擬兩個試驗工況的計算結(jié)果直接獲取了由單元組成的較大碎片以及由SPH 粒子形成的碎片云形貌,其中碎片具有準確的物質(zhì)邊界及形狀,如圖17 所示,與試驗結(jié)果吻合度較高。

圖17 自適應(yīng)耦合算法所得碎片云形態(tài)[119]Fig. 17 The debris cloud of FEM-SPH adaptive method[119]
由圖16、圖17 中碎片云形態(tài)和SPH 粒子分布、較大碎片分布的差異可知,相較于其他文獻,He 等[119]采用改進的FEM-SPH 自適應(yīng)耦合算法所得的計算結(jié)果有一定優(yōu)勢,可直接獲得超高速撞擊后碎片云中較大的危險碎片。在計算中同時使用了Johnson-Cook 失效判據(jù)和最大拉應(yīng)力失效判據(jù),使得低速時彈丸層裂和高速時彈丸完全破碎與試驗結(jié)果均吻合極好。
Johnson 等[99,108-110]、Beissel 等[111-112]、He 等[122]在最初提出的將單元轉(zhuǎn)化為粒子的思想上,對有限元與SPH 方法耦合算法不斷改進,完善了有限元與粒子耦合界面的接觸、連續(xù)性等問題。使用有限元公式計算單元,無網(wǎng)格法公式計算轉(zhuǎn)換后的高應(yīng)變率SPH 粒子,大大提高了計算效率。在此基礎(chǔ)上,眾多學(xué)者根據(jù)需要將其應(yīng)用于研究中,并成功模擬了超高速碰撞問題。但相關(guān)理論對于單元失效的判據(jù)是基于等效塑性應(yīng)變的大小,單元變形接近畸變時即進行SPH 粒子的轉(zhuǎn)化,此時單元并未完全失效,轉(zhuǎn)化成的粒子只能作為單元大變形的表達,所得計算結(jié)果還存在一定的缺陷。
He 等[119]給出的FEM-SPH 自適應(yīng)耦合算法在計算中同時使用了Johnson-Cook 失效判據(jù)和最大拉應(yīng)力失效判據(jù),并且對等效塑性應(yīng)變失效判據(jù)的缺陷進行了修正,計算結(jié)果較好。在研究泡沫、蜂窩等材料時,需要通過細觀建模方法研究其力學(xué)性能。He 等[119]改進的FEM-SPH 自適應(yīng)耦合算法可兼容細觀建模方法,在碎片識別、計算效率等方面具有一定優(yōu)勢,可能是解決復(fù)雜材料超高速碰撞問題的一個有效途徑。
3.3 細觀建模
Whipple 防護結(jié)構(gòu)發(fā)展至今,泡沫、蜂窩、編織等結(jié)構(gòu)復(fù)雜但防護效果較好、密度較低的高性能材料已得到廣泛應(yīng)用,但其受力狀態(tài)下細觀層面的受力分析與破壞模式難以進行準確而詳細的研究。泡沫金屬作為一種高度復(fù)雜的輕質(zhì)多孔材料,在各個領(lǐng)域被廣泛應(yīng)用,人們對其靜態(tài)、準靜態(tài)和動態(tài)下的力學(xué)行為進行了一定的研究。泡沫材料的組成主要由胞孔決定其內(nèi)部分布,其獨特的力學(xué)特性與泡沫的多孔微觀結(jié)構(gòu)息息相關(guān)[52],因此泡沫的細觀建模[123]顯得尤為必要。泡沫金屬細觀建模技術(shù)的研究主要從胞孔結(jié)構(gòu)出發(fā),利用Voronoi 鑲嵌法和CT 掃描法等能夠盡量還原真實的泡沫形態(tài)。
3.3.1 規(guī)則胞孔結(jié)構(gòu)的模擬方法
對于開孔泡沫和閉孔泡沫的細觀建模,部分學(xué)者選擇了較為簡單、規(guī)則的胞孔結(jié)構(gòu),利用重復(fù)性單元按照一定規(guī)則排列模擬泡沫金屬材料,建立細觀模型來研究其宏觀力學(xué)性能和變形特性。
早期學(xué)者們主要采用有限元方法進行細觀建模,選取的胞孔結(jié)構(gòu)均為在多面體的基礎(chǔ)上接近真實胞孔形態(tài)。Gibson 等[124]采用規(guī)則的正立方體胞孔結(jié)構(gòu)模擬開孔泡沫,建立了其細觀模型,Santosa 等[125]建立了由十字形胞壁和金字塔型截面的立方體胞孔結(jié)構(gòu)組成的閉孔泡沫細觀模型,得到了其抗壓強度的計算公式。Li 等[126]則利用十四面體的胞孔單元和卡斯蒂利亞諾第二定理的能量方法建立了3D 開孔泡沫的細觀力學(xué)模型,十四面體模型的所有頂點均通過細長支柱連接,且每個頂點可連接到4 個支柱,忽略橫向剪切效應(yīng),表明開孔泡沫的有效彈性取決于相對泡沫密度、胞壁橫截面的形狀和尺寸,較好地預(yù)測了低密度泡沫的彈性性能。Cheon 等[127]和Tunvir 等[128]選用立方體邊界鑲嵌球體的胞孔結(jié)構(gòu)建立細觀模型研究了閉孔泡沫鋁破碎的力學(xué)行為,得到的抗壓強度理論解比金字塔型胞孔結(jié)構(gòu)的理論解更接近試驗結(jié)果。
由于有限元方法在處理大變形問題上的局限性,部分學(xué)者運用SPH 方法建立規(guī)則胞孔結(jié)構(gòu)的泡沫細觀模型,研究其在超高速碰撞下的破壞行為。馮陽等[129]選擇規(guī)則的球形胞孔結(jié)構(gòu)建立了細觀模型,研究了不同應(yīng)變率下泡沫鋁的變形模式。賈斌等[32]參考工業(yè)化生產(chǎn)泡沫鋁的滲流鑄造法建模,通過調(diào)整球形胞孔的半徑大小來控制泡沫的相對密度,結(jié)合SPH 方法進行離散,研究了填充式泡沫鋁防護結(jié)構(gòu)在超高速撞擊下的破壞行為,與試驗結(jié)果較為吻合。
規(guī)則胞孔結(jié)構(gòu)的泡沫材料細觀模型建立過程較為簡單,其結(jié)構(gòu)具有一定規(guī)律性,可通過有限元和SPH 方法求解,其數(shù)值模擬結(jié)果與試驗結(jié)果較吻合,但仍存在較大缺陷。與實際相比,泡沫鋁胞孔結(jié)構(gòu)的隨機性、不均勻性等特性沒有表達,僅采用規(guī)則的胞孔結(jié)構(gòu)進行周期排列得到的幾何模型,不能真實反映泡沫材料的細觀結(jié)構(gòu)特性。
3.3.2 具有隨機性胞孔結(jié)構(gòu)的模擬方法
為了更真實地反映泡沫結(jié)構(gòu)的細觀特性,部分學(xué)者考慮到泡沫結(jié)構(gòu)胞孔的隨機性特點,通過一定規(guī)則來模擬泡沫的孔隙結(jié)構(gòu)建立細觀模型。其中應(yīng)用比較廣泛的是Voronoi 鑲嵌技術(shù)[130-133],該方法所得到的泡沫模型更接近于實際,能較好地表達泡沫等多孔材料的內(nèi)部結(jié)構(gòu),廣泛應(yīng)用于超高速碰撞模擬[134]。
Zhang 等[135]建立了具有隨機性胞孔結(jié)構(gòu)的泡沫細觀模型,首先確定一組特殊的點,由這些點為中心向外擴張,直到與其他點擴張的區(qū)域連接時停止,這些被劃分出來的區(qū)域即為Voronoi 細胞。用Voronoi方法模擬泡沫結(jié)構(gòu)時,將它應(yīng)用于充滿球體的空間區(qū)域,球體的質(zhì)心即為用于鑲嵌的點,以球體半徑作為權(quán)重來劃分區(qū)域,稱為Laguerre-Voronoi 方法[136-137]。通過球形填充、Voronoi 鑲嵌、顆粒填充建立的有限元模型與泡沫結(jié)構(gòu)試件的對比如圖18 所示,可觀察到模型較好地反映了泡沫結(jié)構(gòu)的隨機多孔特性。

圖18 泡沫材料試件與Voronoi 泡沫模型對比[135]Fig. 18 Comparison of the Al-foam with the Voronoi tessellation model[135]
Wejrzanowski 等[136]以Laguerre-Voronoi 方法為基礎(chǔ)進行改進,采用對數(shù)正態(tài)體積分布得到了一組體積大小隨機的球體,使其在確定區(qū)域內(nèi)隨機運動,并隨著運動過程減小區(qū)域范圍,增加區(qū)域密度直到滿足需求。填充球體后通過Laguerre-Voronoi 鑲嵌法得到細胞結(jié)構(gòu),在相鄰兩個球體表面之間一定距離的相交平面處生成胞壁,沿胞孔單元的邊界生成直徑恒定的圓柱體,最后得到所需的細觀模型,具體步驟如圖19 所示。胞孔大小可通過控制初始球體的大小分布得到,由于其模型采用等直徑的圓柱體來簡化實際中的泡沫結(jié)構(gòu),在孔隙率低于70%時誤差較大,文獻已給出相應(yīng)的矯正方法,該模型的計算結(jié)果整體較準確[138]。
Fang 等[139-140]使用隨機多面體技術(shù)進行建模,并考慮空氣流體和胞壁結(jié)構(gòu)的相互作用,將描述孔隙大小和胞壁厚度隨機性的公式表述為:

式中:N、C 為常數(shù),M 為模運算。
胞壁的隨機厚度可通過以下函數(shù)來實現(xiàn):
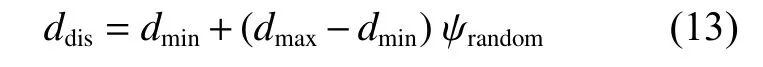
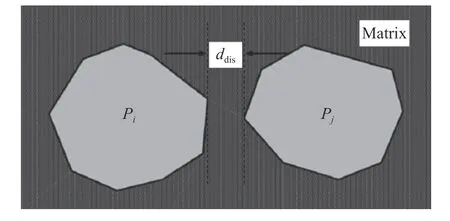
圖20 相鄰兩個孔間胞壁厚度示意圖[139]Fig. 20 Schematic diagram of the cell-wall thicknessbetween the two adjacent pores[139]
式中:ddis為相鄰兩多面體之間的最小距離,如圖20所示,胞壁厚度在dmin~dmax范圍內(nèi)隨機分布。
采用隨機大小和形狀的三維凸多面體,生成所需多面體后,為所有生成的多面體建立隨機列表。判斷生成的多面體凸性,建立具有隨機形狀的3D 凸多面體。最后,采用“take & place”方法生成金屬泡沫的細觀模型(圖21)[144],該模型能可靠預(yù)測閉孔泡沫鋁在靜態(tài)和高應(yīng)變率載荷下的機械響應(yīng)。
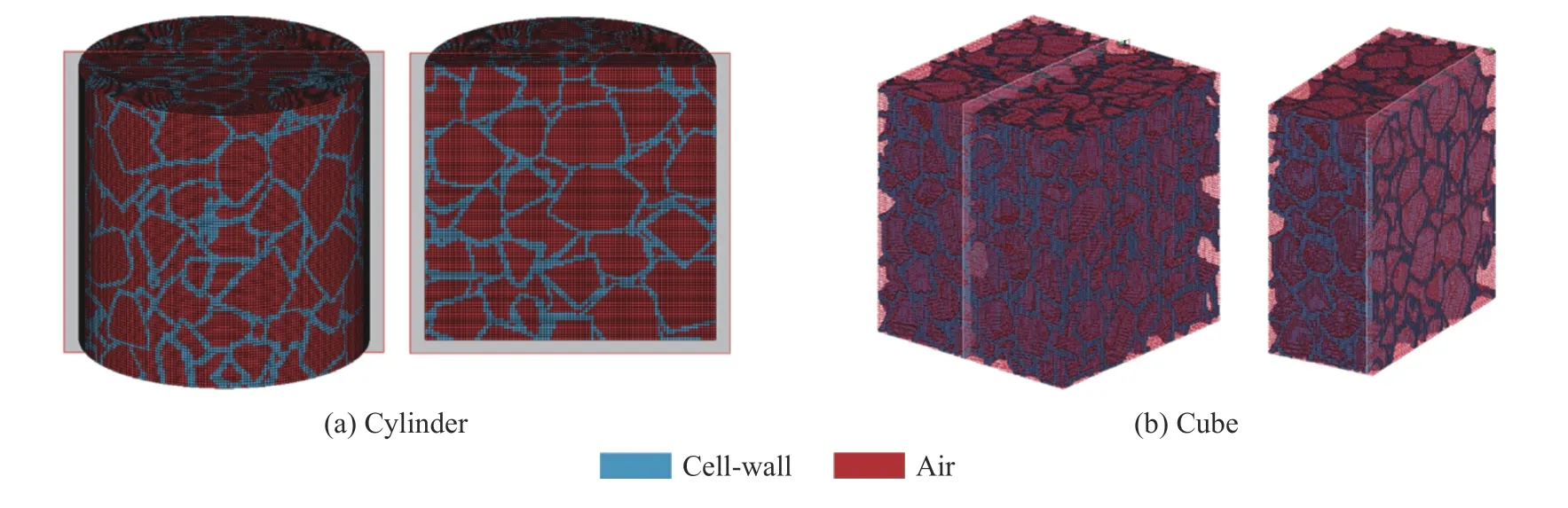
圖21 閉孔金屬泡沫的有限元單元[139]Fig. 21 Finite element grid of closed-cell metallic foams[139]
通過以上方法建立的細觀模型,能更準確地描述泡沫鋁胞孔大小及胞壁厚度的隨機性,相較于規(guī)則胞孔,其內(nèi)部結(jié)構(gòu)復(fù)雜。使用SPH 方法進行計算時,胞孔的隨機性使得SPH 方法建模更加困難,不規(guī)則的粒子分布則放大了計算不穩(wěn)定的缺陷。因此,研究細觀模型在超高速碰撞下的力學(xué)特性時,可考慮先通過建立有限元模型進行計算,在撞擊過程中失效單元逐步轉(zhuǎn)化為SPH 粒子。FEM-SPH 自適應(yīng)耦合算法可與細觀建模方法兼容,二者結(jié)合使用可提高計算精度和計算效率,且能夠得到更接近實際結(jié)構(gòu)破壞行為的計算結(jié)果。
3.3.3 CT 掃描法
泡沫結(jié)構(gòu)細觀建模的CT 掃描法是指利用CT(computed tomography)掃描技術(shù)得到真實的泡沫橫斷面圖像,再根據(jù)圖像進行三維重建獲得泡沫的細觀模型[145-152]。陳鵬等[149]利用CT 掃描法建立了較真實的泡沫材料細觀結(jié)構(gòu)模型并開展了力學(xué)性能研究,與試驗結(jié)果吻合較好。程振等[151]根據(jù)閉孔泡沫鋁CT 掃描圖像的幾何特征,選擇與胞孔結(jié)構(gòu)類似的橢球來模擬胞孔,并提出了橢球體的隨機生成算法和隨機投放算法來建立三維細觀模型。李侯貞強等[152]則根據(jù)CT 掃描圖像和映射單元思想,利用自編程序判別材料屬性,建立了閉孔泡沫鋁的細觀模型,通過直接生成節(jié)點和單元,避免了三維重建過程中單元剖分質(zhì)量控制的問題。
圖22 為CT 掃描灰度圖像和有限元模型截面的對比,同一位置二者孔隙率之間誤差極小,不同截面中二者的胞孔形狀和胞壁結(jié)構(gòu)均具有很高的一致性。CT 掃描法可建立更符合泡沫鋁內(nèi)部實際結(jié)構(gòu)的模型,較真實地反映泡沫的細觀結(jié)構(gòu)特性及靜態(tài)力學(xué)性能,能夠更細致地研究泡沫鋁的動態(tài)力學(xué)性能及超高速撞擊下的破壞形態(tài)。但CT 掃描法對試驗設(shè)備要求較高,有限元模型復(fù)雜且需大量單元,計算時間與計算成本較大。
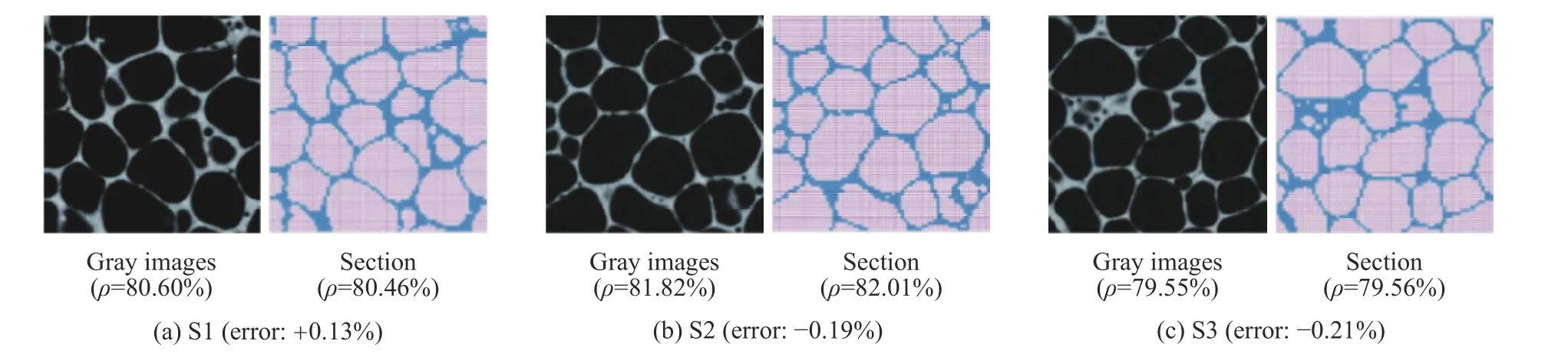
圖22 有限元模型不同截面和CT 掃描得到的灰度圖像對比[152]Fig. 22 Comparison of different section and gray images of finite element model[152]
4 總 結(jié)
Whipple 防護結(jié)構(gòu)的發(fā)展主要體現(xiàn)在防護板結(jié)構(gòu)和材料的改變上。由傳統(tǒng)的單層板簡單結(jié)構(gòu)逐漸發(fā)展成多層板結(jié)構(gòu)。但多層板結(jié)構(gòu)受到體積與質(zhì)量的限制,無法達到最佳防護配置的空間要求。為簡化結(jié)構(gòu),充分利用體積優(yōu)勢,防護性能優(yōu)異的填充式防護結(jié)構(gòu)與夾芯板防護結(jié)構(gòu)得到廣泛應(yīng)用。對比不同結(jié)構(gòu)的彈道極限曲線,在超高速撞擊下,填充式防護結(jié)構(gòu)的防護性能最優(yōu)。中間層的材料選擇為填充式防護結(jié)構(gòu)的變化提供了更多可能,Nextel 纖維、Kevlar 纖維、金屬蜂窩、金屬泡沫等高性能材料的應(yīng)用,可有效提升防護板強度。
Whipple 防護結(jié)構(gòu)的發(fā)展得益于試驗和數(shù)值模擬方法的共同發(fā)展。研究超高速碰撞問題時,傳統(tǒng)的有限元方法受限于大變形下單元的畸變與失效,無法給出計算結(jié)果,因此需要用到SPH 方法。但SPH 方法難以建立復(fù)雜結(jié)構(gòu)的細觀模型,在細觀建模和計算時,物質(zhì)邊界不明確、計算不穩(wěn)定、碎片識別困難等缺陷對計算結(jié)果影響較大。為此,學(xué)者們對SPH 方法進行改進,結(jié)合有限元方法與SPH 方法的優(yōu)點提出了FEM-SPH 自適應(yīng)耦合算法,將失效的單元轉(zhuǎn)化為SPH 粒子,大大提升了計算效率。
泡沫和蜂窩結(jié)構(gòu)的多孔特性使得其在與較小尺寸的碎片作用時,內(nèi)部孔隙結(jié)構(gòu)能夠?qū)λ槠朴行У貙嵤┒啻渭虞d,提高碎片液化、氣化的比例。對于含復(fù)雜結(jié)構(gòu)材料的Whipple 防護結(jié)構(gòu),需要建立細觀模型來進行超高速碰撞下細觀層面的受力分析與破壞模式研究。細觀建模的難點在于:復(fù)雜結(jié)構(gòu)的形狀使得細觀模型在劃分單元時不易保證單元質(zhì)量;細觀建模的單元尺寸與整體模型一般會相差多個數(shù)量級,導(dǎo)致單元數(shù)量過于龐大,對求解設(shè)備要求較高。采用CT 掃描法建模時,相關(guān)要求更加苛刻。相對于CT 掃描法,通過Voronoi 鑲嵌等方法建立具有隨機性胞孔結(jié)構(gòu)的細觀模型,其計算量較小。
將FEM-SPH 自適應(yīng)耦合算法應(yīng)用于碎片云問題研究,可模擬給出與試驗結(jié)果相似的碎片云形態(tài),并能夠直接得到由單元組成的體積較大的危險碎片。He 等[119]提出當細觀模型均由拉格朗日單元構(gòu)成時,在細觀建模的基礎(chǔ)上使用FEM-SPH 自適應(yīng)耦合算法,可求解泡沫、蜂窩、梯度和編織材料等復(fù)雜結(jié)構(gòu)的超高速碰撞問題。該算法可有效避免單一方法的缺陷影響,為研究復(fù)雜材料及結(jié)構(gòu)在超高速碰撞問題中的響應(yīng)提供了條件,可能是解決超高速碰撞問題的一個有效途徑。

