土壤水分布的孔隙尺度格子玻爾茲曼模擬研究1)

胡五龍 劉國峰 晏石林 范嚴偉

?(武漢理工大學綠色智能江海直達船舶與郵輪游艇研究中心,武漢 430070)

? (武漢理工大學理學院,武漢 430070)

??(蘭州理工大學能源與動力工程學院,蘭州 730050)

引言

土壤是人類、植物及微生物維持生命活動所需水分及營養物質的重要來源[1];同時也是生態循環的主要組成部分[2].水在土壤孔隙中的分布直接影響土壤中物質,包括水、空氣及其他有機或無機物質的存儲及傳輸[3],并對土壤中微生物的活動范圍及強度有著決定性的影響[1].

土壤中水分分布一直廣受農業、環境、生態等領域研究人員的關注,并在不同角度不同尺度得到了大量的研究.例如周啟友和島田純[4]通過野外觀測及反演計算,探討了土壤水在空間分布的非均質性及各向異性.張常亮等[5]通過對天然降雨入滲后黃土中不同深度土層體積含水率為期一年的監測數據進行分析,確定了黃土地區降雨入滲深度及浸潤線以下水分遷移特點.杜娟等[6]采用野外觀測手段研究了沙漠不同地形下土壤中水分時空變化特征,發現土壤滲透性與孔隙結構、有機質及水分分布有密切關系.這些研究加深了人們對土壤水分時空分布變異性及復雜性的理解,但大部分研究都是對宏觀現象的描述,土壤中的所有物理過程及生化反應都發生在孔隙中,從孔隙尺度模擬非飽和土壤中水及溶質的分布,有助于對土壤中各過程和反應的理解.

土壤一般為非飽和狀態,土壤中水的運動實際是復雜的多相流,在相當長時間內,對于土壤水問題一直停留在定性描述或采用各種經驗方法處理的層面上[7].自1856 年Darcy[8]在大量實驗的基礎上提出達西定律,1907 年Buckingham[9]提出毛管勢理論,到1931 年Richard[10]在達西定律的基礎上推導出用于描述非飽和流的方程,土壤水運動理論模型逐步建立起來.此后土壤水運動研究的關注點轉移到了基本方程的求解,而其中的關鍵之一是土壤水分特征參數的確定,1964 年Brooks 和Corey[11]建立了飽和度、壓力梯度及水力特性之間的關系,并提出利用毛管壓力?飽和度曲線來確定水力特性的方法;van Genuchten[12]提出了估算非飽和土壤水力特征的半經驗公式,該公式后來成為了描述土壤水力特性的主要公式之一.還有一些其他方法,包括轉換函數和神經網絡等也被用于土壤水力特征及土壤水運動的研究中[13-14].國內邵明安等[15-16]也在土壤水運動、水力特征參數測量與計算方面做了大量的基礎研究工作.2019 年Jin 等[17]在前人模型基礎上,將薄膜流模型和毛管流模型進行整合,提出了一種可以描述全飽和度區間土水特征曲線的分形模型.以上這些模型對于理解和模擬土壤中水的分布起到了非常關鍵的作用,但此類模型及其參數都是土壤宏觀特征的平均表征,直接從孔隙尺度研究水在每個孔隙中的具體形態和分布,有助于理解影響水分分布的因素及其作用機理,并改進宏觀模型.早期的孔隙尺度模擬方法是將真實的土壤孔隙結構簡化為由不同形狀和尺寸的毛細管道組成的毛管束[18],或簡化為由不同孔隙空間和喉道組成的孔隙網絡[19],然后基于這些毛管束或孔隙網絡模型模擬孔隙管道中的流體運動.毛管束模型和孔隙網絡模型為研究土壤中的物質輸運和化學過程提供了很大幫助[20-22],但其無法反映土壤的真實孔隙結構和連通特征,因此其在模擬土壤結構和水力特征方面往往存在較大誤差[23].

顯微成像技術,尤其是X 射線斷層掃描技術(XCT)的發展,使直接觀測土壤中微納米尺度物質及孔隙分布成為了可能[24].但目前的X-CT 和圖像處理技術仍很難辨別土壤中的水和空氣,更難直接觀測土壤中的動態過程[25-26],因此仍需要結合孔隙尺度模擬方法來研究土壤中的流體動力學問題.利用X-CT 獲取土壤的真實三維孔隙結構,結合計算流體力學(CFD)方法可直接模擬流體物質在孔隙中的運動.直接孔隙尺度模擬中常用的CFD 方法主要包括基于粒子的格子玻爾茲曼方法[27-28](LBM)和光滑粒子動力學方法[29](SPH),以及基于網格的水平集方法[30](Level Set)、流體體積法[31](VOF)以及有限體積法[32](FVM)等.這些CFD 方法在模擬孔道中流動問題方面各有優劣勢[33],其中LBM 因其在處理復雜邊界及多相流方面具有天然優勢,并且方便并行化計算,近年來得到了迅速發展[34-37].目前應用的LBM多相流基本模型主要有三種：顏色函數模型[38-39]、自由能模型[40-41]和Shan-Chen 偽勢模型[42-44],本文選用偽勢模型進行模擬研究.偽勢模型通過引入偽勢來描述流體粒子之間的相互作用,具有較好的物理意義,并且易于程序實現,因此得到了較廣泛的應用.但該模型缺少熱力學一致性,在模擬大密度比的多相流時容易造成數值不穩定,雖然通過改進狀態方程和力項,使模型適用的密度比有了很大的提升[43],但是在模擬真實的復雜孔隙結構中多相流時仍非常困難,尤其是對于孔隙直徑分布廣且微孔較多的孔隙結構.

土壤作為強非均勻性的多孔三相系統,具有從納米尺度至毫米尺度豐富的孔隙結構,而土壤中的物理及生化反應都發生在孔隙壁面,即液?固或氣?固界面處.接觸角反映了土壤固相的潤濕性,控制著土壤孔隙中水的狀態及分布.最近研究表明植物根系分泌物[45]、微生物活動產物[46]及有機物[47]會改變土壤顆粒表面的潤濕性,并進而影響土壤孔隙中的水分分布.流體與固體壁面的接觸角通常都采用實驗方法測得,但是對于結構復雜的多孔介質,通過實驗觀測流體在孔隙內的流動非常困難.利用LBM 孔隙尺度模擬流體接觸角是一種簡便可行的辦法,自Briant[48]于2004 年提出利用LBM 來模擬多相流體的接觸線運動,此后LBM 被經常用于流體接觸角研究,尤其是模擬液滴在材料表面的行為.張博[49]將LBM 應用于材料領域,分析了液滴潤濕行為與材料表面微納結構的關系.方可寧等[50]利用LBM 對加熱基板上的液滴進行模擬,研究了不同接觸角液滴的鋪展及蒸發過程.胡夢丹等[51]采用LBM 對結構表面液滴的冷凝行為進行模擬研究,分析了材料表面的幾何尺寸和接觸角的局部不均勻性對冷凝液滴形核位置及最終潤濕狀態的影響規律.這些研究都是通過LBM 方法模擬液滴在材料表面或簡單管道中的運動狀態,鮮見針對真實三維孔隙結構中多相流的模擬,更無對土壤中孔隙水受接觸角影響的模擬研究.

本文采用改進的Shan-Chen 格子玻爾茲曼模型,直接模擬了不同接觸角情況下水分在土壤孔隙中的分布,探討了接觸角對孔隙水分分布狀態的影響,以期為進一步模擬土壤中流體運動及物質遷移提供基礎,并為土壤水資源研究及優化農業生產提供理論指導.

1 格子玻爾茲曼方法

在格子玻爾茲曼模型中,流體的運動被描述成一系列離散的單密度分布函數.標準的格子玻爾茲曼方程可表示為[52]

其中fi(x,t)為流體粒子密度分布函數,i表示速度離散方向;為平衡態分布函數;τ 為無量綱松弛時間;c=?x/?t,為流體粒子的格子速度;?x和?t分別為格子尺寸和格子時間步長,一般取1.F(x,t)為流體粒子受到的作用力,一般包括流流作用力Fint(x,t)、流固作用力Fs(x,t)以及其他外體力Fb(x,t).由于土壤中水受到的基質吸力遠大于重力,因此本文研究中忽略了重力影響.

本文采用D3Q19 格式,即將粒子速度在空間上按照19 個方向進行分解,如圖1 所示.離散后i方向的速度ei可表示為[53]

ρ 和u分別表示格點處的宏觀密度和速度;wi為權重系數,在D3Q19 格子系統中取[53]

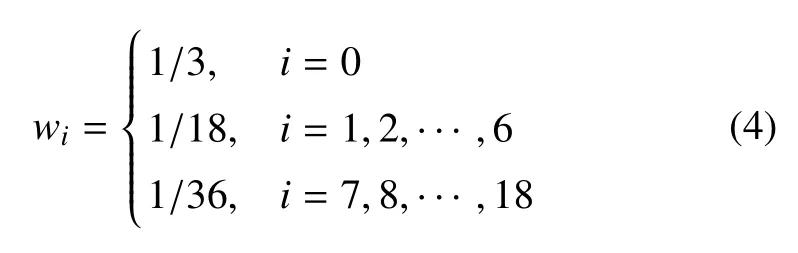
流體密度ρ 和速度u可通過流體粒子分布函數的一階矩和二階矩求得

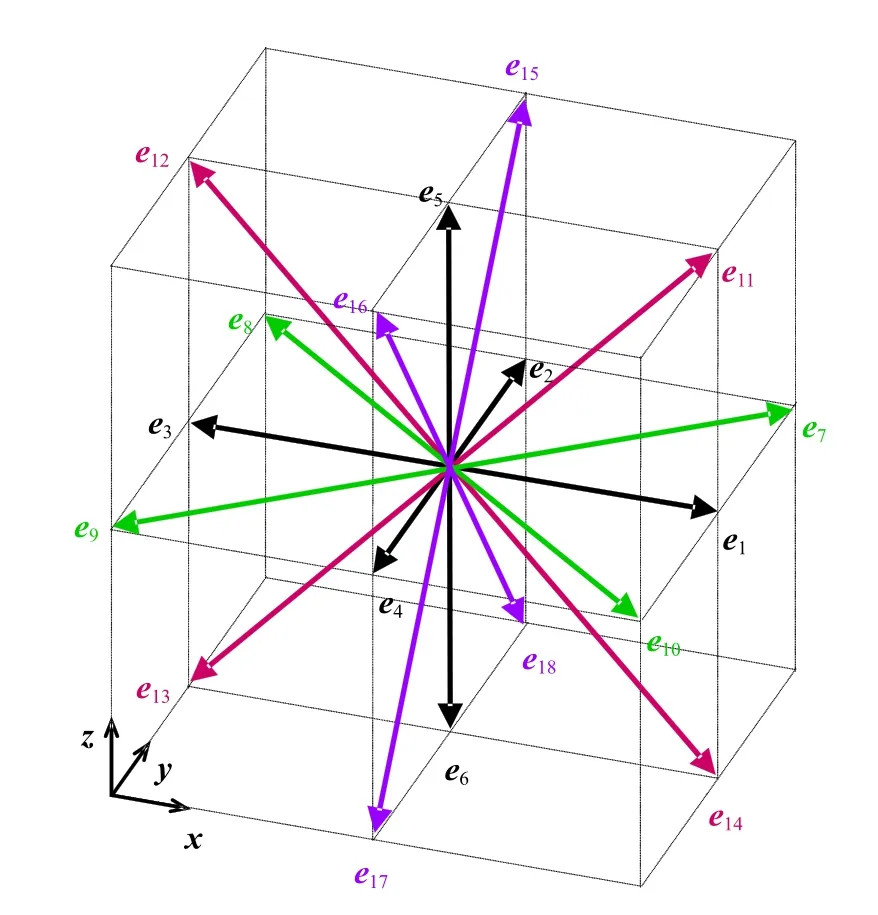
圖1 D3Q19 LBM 速度離散模型示意圖Fig.1 Schematic sketch of LBM discrete velocities in the D3Q19 scheme

1.1 流流作用力

在Shan-Chen 模型中,流體粒子之間的相互作用力可表示為[55]

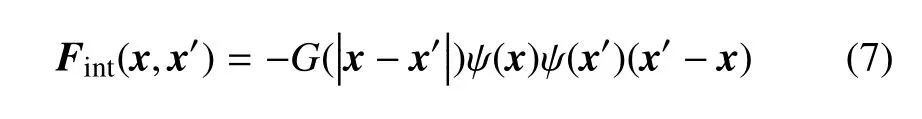
其中ψ 為偽勢函數,或稱有效質量,是流體密度的函數;G為格林函數,表征流流粒子間相互作用力強度,控制液、氣相的分離及液氣界面的表面張力,G<0表示流體粒子相互吸引.對于D3Q19 模型,格林函數為[56]

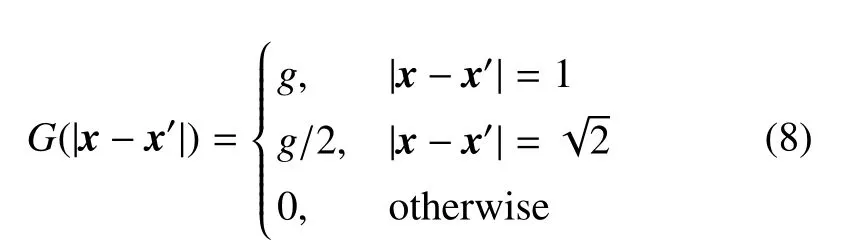
g為流流作用力強度系數.x位置處的流體粒子受到周邊流體粒子作用力的合力為[55]

1.2 流固作用力

流體粒子與固相的流固作用力用下式表示[55]

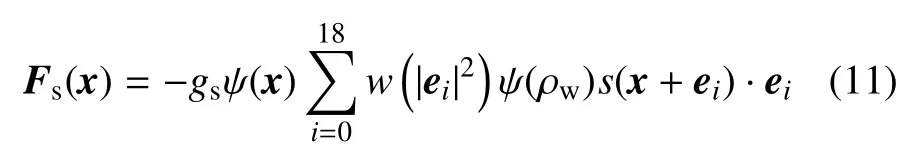
式中gs為流固作用系數,表征流體粒子與固相之間的作用力強度.在有固相的LBM 中,g與gs共同決定液固的本征接觸角,但在本文,由于對模型進行了改進,采用的Peng-Robinson(P-R)狀態方程,最終接觸角僅依賴于gs.s(x+ei)為標示函數,當(x+ei)為固相時,s(x+ei)=1;當(x+ei)為流體時,s(x+ei)=0;ψ(ρw)取固定值1.

1.3 模型改進

在Shan-Chen 模型中,Fint(x)??c0ψ(x)g?ψ(x)對應的狀態方程為,偽勢函數可表示為

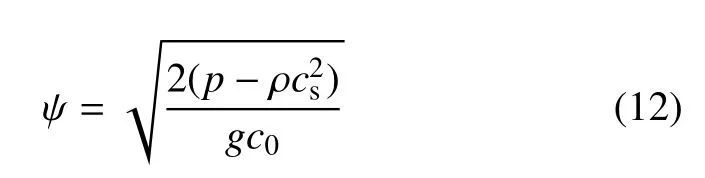
其中c0為常數,對于D3Q19 模型,c0=6[53].

很多研究已經表明,原始的Shan-Chen 模型不適用于密度比大的多相流體.而實際上,無論是水和水蒸氣還是油與氣,其密度比都達到好幾百甚至上千.采用接近真實流體的狀態方程可以大幅度提高LBM適用的密度比,本文采用P-R 狀態方程,改進后模型實現的最大密度比超過7000.

P-R 狀態方程為

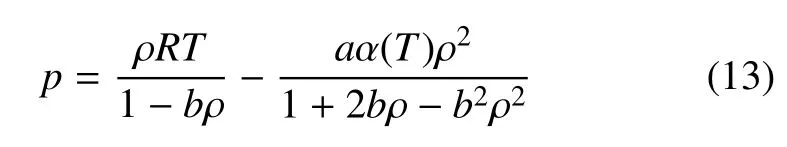
α(T)={1+(0.374 64+1.542 26ω ?0.269 92ω2)×[1 ?(T/Tc)0.5]}2,ω 為偏心因子,對于水,ω=0.344;T為溫度,Tc為臨界溫度;a=,b=0.077 8RTc/pc.本文計算中取a=1/49,b=2/21[43].

為減小模型計算中產生的偽流,提高穩定性,將流體粒子間作用力改寫為

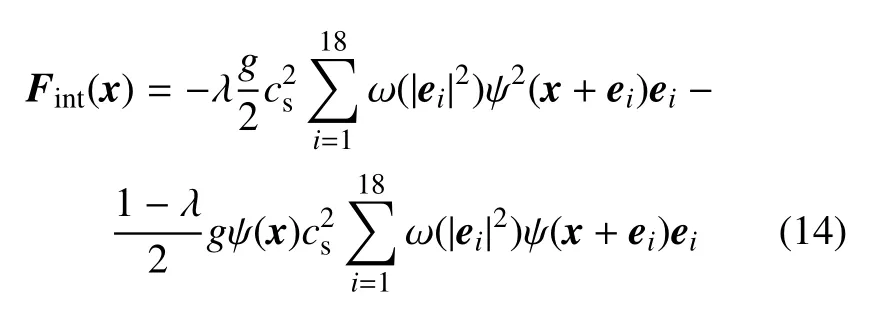
在引入作用力時采用精確差分法(EDM),此時,外力項為

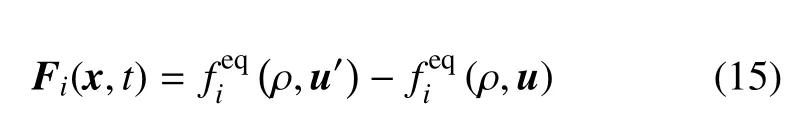
其中u通過式(6)求得,而u′=u+F?t/ρ.EDM 方法可以提高模型的熱穩定性,結合以上方法,該LBM可模擬的最低溫度達0.4Tc.

2 材料及土樣

本文選取兩個多孔材料的X-CT 圖像作為模擬對象,如圖2 所示,其中模擬土樣是由微小玻璃珠粘結而成,孔隙結構相對比較均勻,尺寸為150×150×150 像素(voxel),像素分辨率為40 μm,孔隙率為0.368 1,后文用土樣1 表示;真實土樣為2015 年取自英國洛桑實驗站的Highfield 草地試驗田(51.810 3N,?0.374 8E),該試驗田為粉質黏壤土,其基本理化性質見文獻[58]表1 中的Grassland,后文用土樣2 表示.土樣2 的提取過程如下：將田間提取的土壤樣芯振碎,然后分別過孔徑為4 mm,2 mm 和0.71 mm 的篩子,隨機挑選0.71～2 mm 的團聚體,再將挑選的團聚體通過Phoenix Nanotom 掃描系統進行X-CT 掃描,掃描電壓和電流分別為90 kV 和65μA,分辨率為1.51μm.拍攝曝光時間為500 ms,整個土樣掃描時間為69 min,共獲取1440 張投影圖片.利用掃描系統配套的軟件Phoenix datos|x2 將投影圖片重構為三維圖像,并導出三維圖像的原始連續切片圖,然后利用開源軟件ImageJ (https://imagej.nih.gov/ij/)將圖片進行二值化處理,土樣2 的詳細獲取及處理過程見文獻[58].由于獲得的土樣初始圖像較大,為減少計算量,截取200×200×200 像素的立方體作為本文研究的土樣2(如圖2),其孔隙率為0.232 5.為便于分析,本文中所有物理量包括長度、密度等均直接采用格子單位,其都可以轉換成實際的物理單位,1 lu=1 voxel(lu 為格子單位).

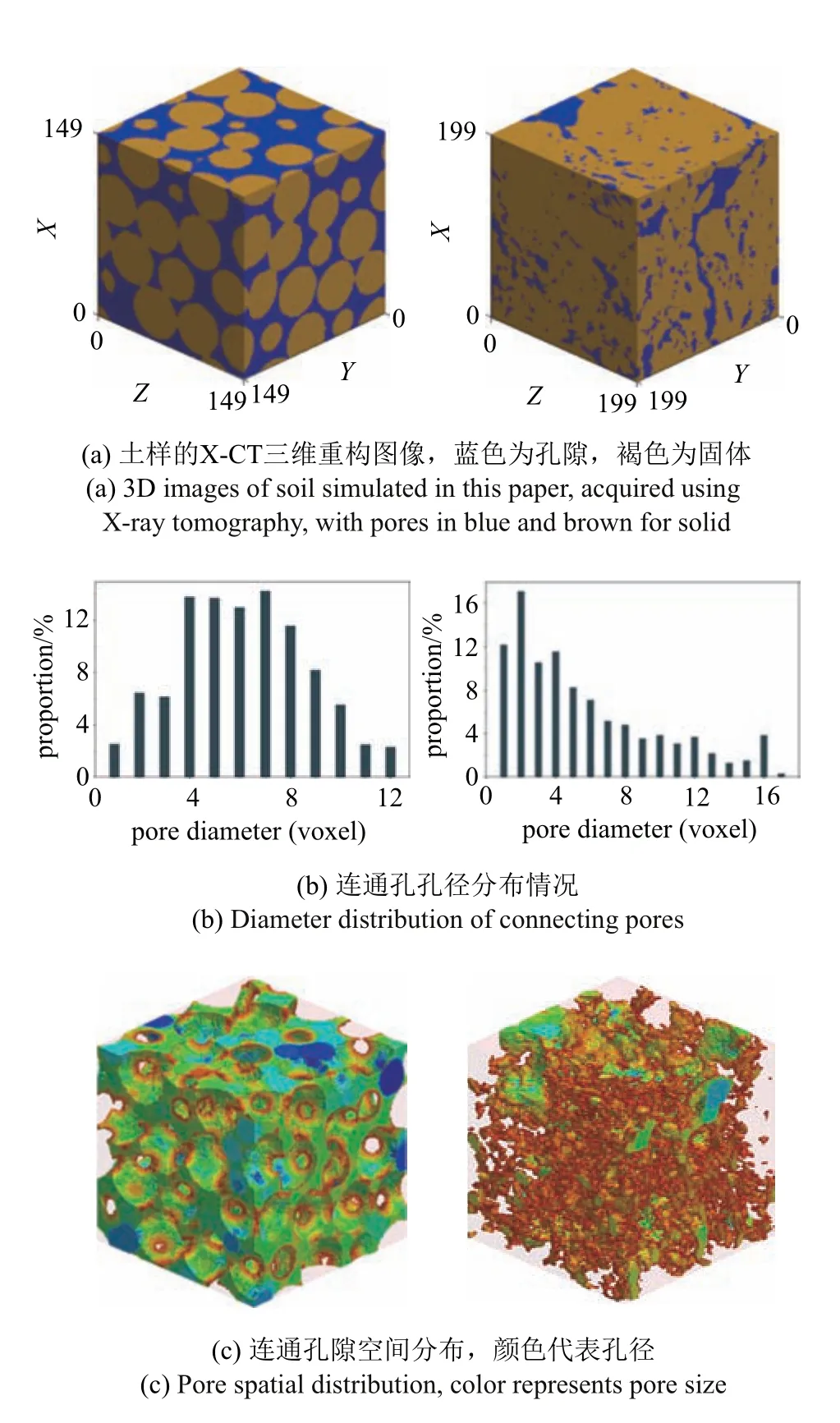
圖2 兩個土樣的三維結構:左邊是模擬土樣(土樣1),右邊是真實土樣[58] (土樣2)Fig.2 Three dimensional structure of two soils used in the simulations,the artificial soil shows in left column and real soil shows in right

假定水只在連通孔隙中流動,為減少模擬中的計算量和所需內存,計算前先提取連通孔隙,并采用形態模型[59]計算每個孔隙的直徑.兩個土樣的連通孔隙結構分別如圖2 所示,土樣1 的平均孔徑為6.12像素,土樣2 的平均孔徑為5.68 像素.由圖可以看出兩個土樣的孔隙結構有明顯差異,其中土樣1 連通孔隙率為0.368,孔徑分布為正態分布,而土樣2 連通孔隙率為0.221,孔徑分布近似泊松分布.

3 計算結果及討論

3.1 接觸角計算

研究表明大部分土壤既不是完全親水的,也不是疏水的,即接觸角在0?～90?范圍內變化[47,60].在微生物或植物根系的作用下,土壤與水的接觸角會發生變化,但仍屬于親水物質,因此本文只研究接觸角小于等于90?的情況.

假定式(10)中ψ(ρ)=1,改變gs的值,即可獲得不同的接觸角.為獲取接觸角與gs之間的關系,先模擬一個水滴在固體平面上的穩定狀態.如圖3(a)所示,構建一長寬高(XYZ)分別為200 lu×200 lu×100 lu 的空間,下邊界設置2 lu 厚的固體平面,其他邊界均設置為周期邊界,固體壁面采用反彈邊界條件.系統恒溫,溫度設置為T=0.7Tc,Tc為臨界溫度.初始時刻在固體平面中央放置一長寬相等有一定高度的方體液滴,密度為ρl0;其余空間為水蒸氣,密度為ρv0,如圖3(a).每1000 次迭代計算輸出一次結果,當兩次輸出的液態水體積分數變化小于10?7時,則認為水的空間分布已經達到穩定狀態.設液態水與水蒸氣的臨界密度ρc=(ρl0+ρv0)/2,圖3(b)和圖3(c)為穩定后的液態水在平面上的形態.

液滴達到穩定狀態后,測量液滴的高度h、液滴與固體平面接觸面直徑d,則接觸角θ 可通過下式計算得出

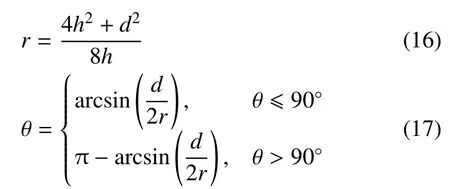
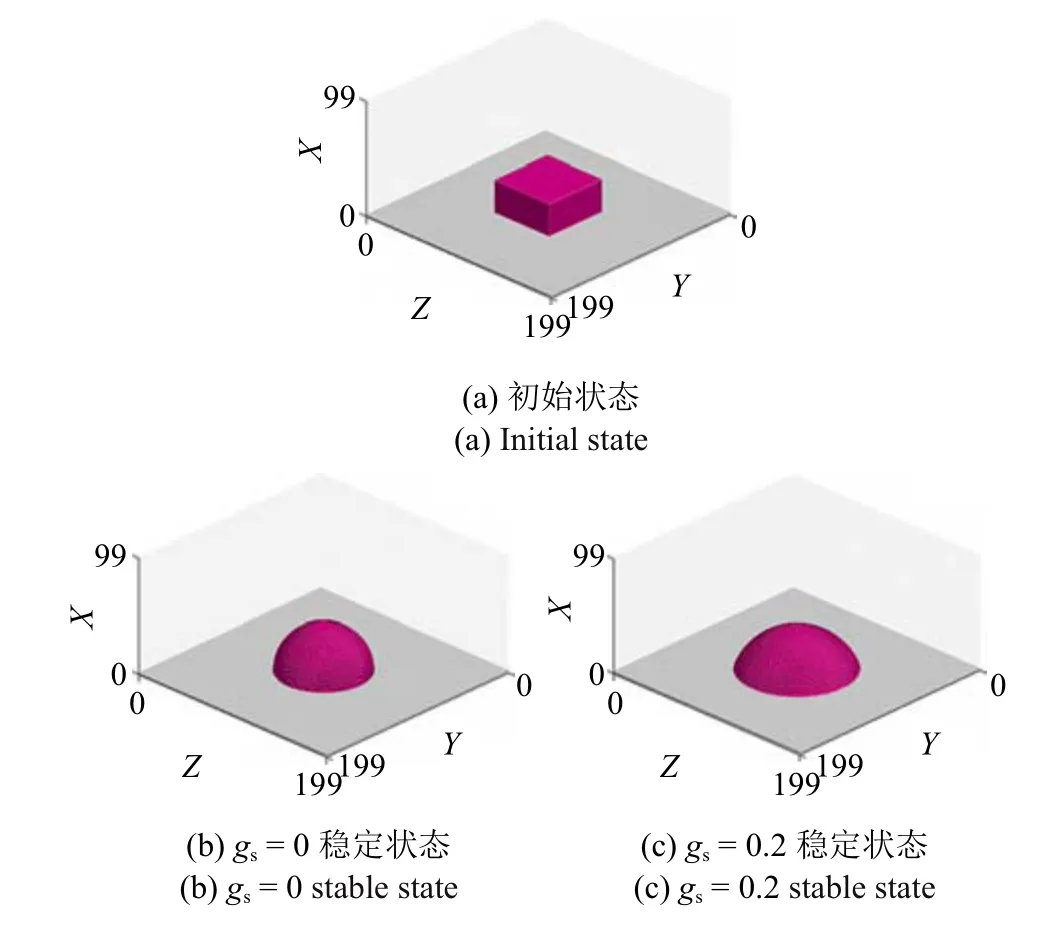
圖3 水滴在固體平面上的狀態變化Fig.3 The state of liquid water on a solid plane

計算得到的接觸角θ 與gs值如圖4 所示,其關系可用直線θ=?114gs+90?近似表示,假設土壤中水的接觸角θ 與gs也服從此規律,則后文中接觸角θ均可由gs依據此公式求得.土壤孔隙中的流體接觸角不僅與固液氣相互作用及液體表面張力有關,還受孔隙直徑、壁面粗糙度的影響,但對于同一土樣,其固體組分及內部孔隙結構不變,流體接觸角僅隨gs而改變,因此以上假設不會影響本文的研究.

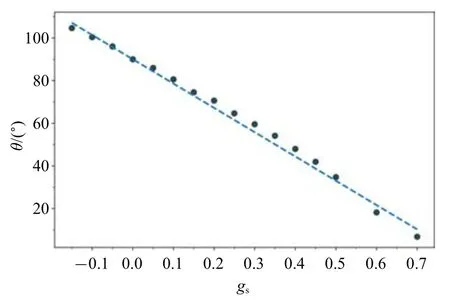
圖4 T=0.7Tc時液滴與光滑固體平面接觸角θ 與gs的關系Fig.4 Relationship between contact angle θ of droplet on smooth solid plane and gsunder temperature T=0.7Tc

3.2 接觸角對土壤水分布的影響

假定土壤孔隙中的水分布由毛管壓力p∝cos θ·σ/d控制,其中σ 為氣水表面張力,θ 為接觸角,d為孔隙直徑.對于給定的接觸角和表面張力,每個孔都對應一毛管壓力.假定土樣的底面與水液壓相連,并施加吸力p,在毛管壓力與吸力p的共同作用下,水就會進入土樣中毛管壓力小于p且連通的孔隙[59].依據上述方法對土樣1 設置初始水分分布,然后模擬不同θ 情況下水分在土樣中的運動及重分布,土樣1 的初始飽和度約為0.35.模擬中土樣的所有邊界均設置為周期邊界,固體壁面采用反彈邊界條件.溫度T=0.7Tc,每迭代計算1000 次輸出一次結果,當兩次輸出的液態水體積分數變化小于10?7時,則認為此時刻土樣孔隙中的水分分布已經達到穩定狀態.土樣1 在不同θ 情況下的水分布如圖5 所示.在不考慮重力的情況下,θ=90.0?時,液態水和水蒸氣分散分布于土壤的所有孔隙,與孔隙直徑無關.隨著θ 減小,液態水的分布逐漸轉移到固體土顆粒附近,緊密圍繞固體土顆粒,形成水膜.

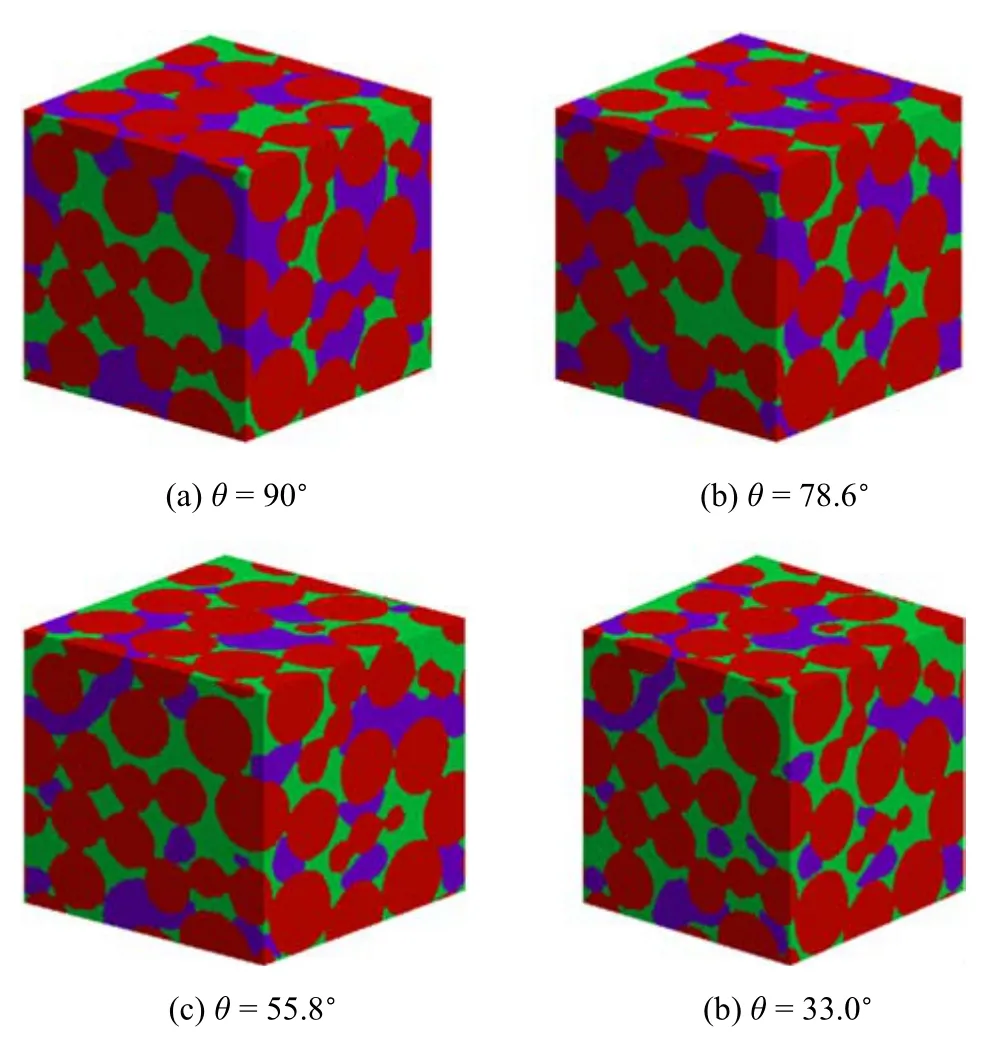
圖5 不同θ 情況下土樣1 孔隙中液態水及水蒸氣的分布:紅色為固體土顆粒,綠色為液態水,紫色為水蒸氣Fig.5 Distribution of liquid and vapor water in soil 1 under different contact angles θ,with solid in red,liquid in green and vapor in purple

圖6 展示了不同θ,水蒸氣在土樣1 中的分布.當θ=90.0?時,水蒸氣的分布圖像棱角尖銳,即水蒸氣在大孔隙與小孔隙中均有分布,說明接觸角接近90.0?時,土壤固體壁面的表面自由能較低,對液態水的吸引力較弱;此時土壤中的毛管吸力幾乎為零,孔隙中水的基質勢為零.隨著θ 減小,水蒸氣的分布圖像棱角逐漸變得圓滑,即水蒸氣逐漸被擠出小孔隙,說明隨著接觸角減小,固體壁面對液態水會產生較大的吸引力,導致液態水會迅速填充孔徑較小的孔隙,并排擠出氣態水,使水蒸氣在大孔隙中匯集形成氣泡;土壤中的毛管吸力隨接觸角減小而增大,此時孔隙水由于土壤固相的吸附產生負的基質勢,并且其值隨接觸角減小而減小.

圖6 不同θ 時水蒸氣在土樣1 中的分布Fig.6 Spatial distribution of vapor(red)in simulated soil under different contact angles θ;the voxels of solid and liquid were made transparent

土壤中的物理及生化過程都發生在界面處,因此在研究土壤中水分布時需要進一步分析流體與固體以及流體與流體之間的界面面積.接觸角會影響液態水與空氣的分布,也必然會影響液固、氣固及液氣界面面積.為此對土樣1 中不同接觸角情況下的液固(LS)、氣固(VS)及液氣(LV)界面面積(A)進行統計,為研究方便,對所有界面面積A均除以土樣的固相總表面積A0進行無量綱化.結果如圖7 所示,LS和LV 的面積均隨θ 增大而減小,而VS 的面積隨θ增大而增大.

圖7 土樣1 中液固(LS)、氣固(VS)及液氣(LV)界面面積(A/A0)隨θ 的變化Fig.7 Changes of interface area(A/A0)in soil 1 with contact angle θ

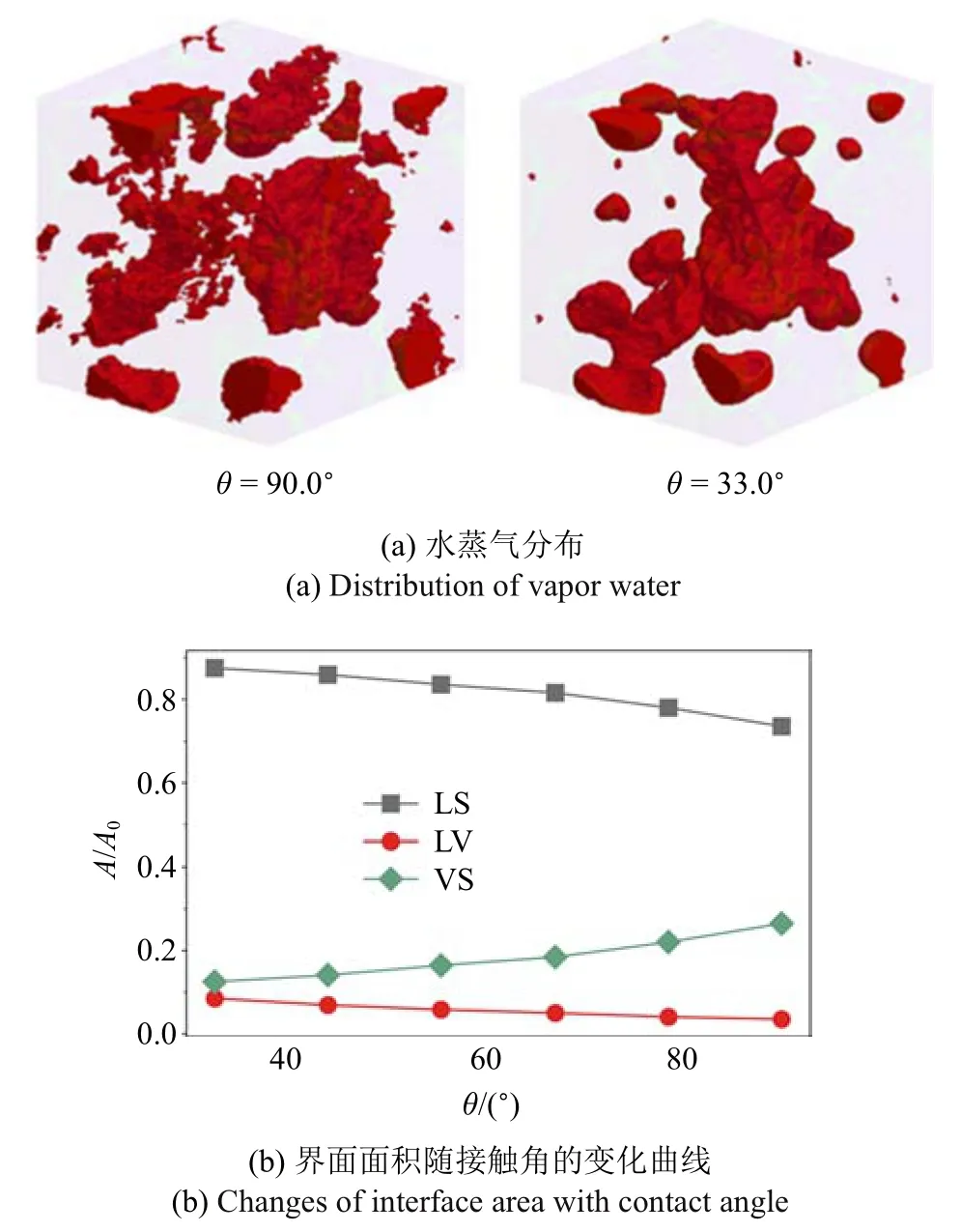
圖8 土樣2 的驗證結果Fig.8 Verification results of soil 2

為驗證以上規律對其他土樣是否也成立,選用一個孔隙結構與土樣1 相差較大且非均勻性強的土樣2 (如圖2),按照前面的方法模擬飽和度約為0.60時,不同θ 情況下土樣中液態水及水蒸氣的分布.結果與土樣1 一致,如圖8 所示,在土樣2 中,隨著接觸角減小,液態水進入貼近土壤固相表面的小孔隙,并沿著固相表面擴展形成水膜;氣態水逐漸被擠入大孔隙形成氣泡;液態水的表面面積隨θ 減小而增大,而水蒸氣與固體的界面面積隨θ 減小而減小.由圖7與圖8(b)對比發現,雖然兩個土樣中LS,LV 及VS 隨θ 變化規律相同,但土樣1 中的曲線變化明顯比土樣2 的更顯著,這是由于土樣1 飽和度較低,在θ 較大時,大部分小孔隙仍未被液態水填充,LS 界面面積小于VS 界面面積;隨著θ 減小,液態水進入小孔隙,導致LS 界面面積顯著增大,而VS 界面面積減小.土樣2 中孔隙結構非均勻性很強,有非常多的小孔隙,但由于土樣2 的飽和度較高,大部分小孔隙在θ 較大時就已被液態水填充,因此LS 及VS 界面面積隨θ 變化較小.

3.3 接觸角對物質輸運通道直徑的影響

由式(17)可知接觸角由液滴在固體表面的厚度(h)和接觸面直徑(d)決定,其中d影響液固和氣固界面面積;而h決定液態水和水蒸氣的厚度,在三維孔隙結構中即為液態水和水蒸氣占據的孔隙直徑,后文中直接簡稱液態水或水蒸氣厚度,用hl和hv表示.若將土壤中液態水看作水及溶質運移的通道,而將水蒸氣看作氣體輸運的通道,則hl和hv實際分別是土壤中液體和氣體的輸運通道直徑.采用前面提到的計算孔隙直徑的方法,分別計算hv和hl.在不同θ,土樣1 中液態水的平均厚度ˉhl均隨θ 減小而減小,而ˉhv則均隨θ 減小先增大后減小,如圖9(a)所示.這是由于隨著θ 減小,水優先填充小孔隙,積聚在大孔隙中的液態水沿著土壤固相表面擴展,形成水膜,液態水的厚度hl減小,hv則相應增大;但是當θ 減小到一定程度后,液態水充滿所有小孔隙,并且逐漸浸潤了大孔隙的固相表面,使原來在大孔隙中與土壤固相接觸的水蒸氣脫離固相表面,形成游離在液態水中的氣泡,hv減小.對于土樣1,ˉhl和ˉhv均可以用公式ˉh=αθ2+βθ+A進行擬合,兩個土樣的擬合結果如圖9(a)中曲線,擬合參數值如圖9 所示,參數α,β 值與土壤的孔隙結構及飽和度有關.為驗證以上規律與土壤孔隙結構無關,又計算了土樣2 中不同gs的hl和hv,結果如圖9(b)所示.在土樣2 中,hl和hv隨θ 的變化規律與土樣1 相同,ˉhl和ˉhv也可以擬合為二次多項式.

3.4 水分密度分布

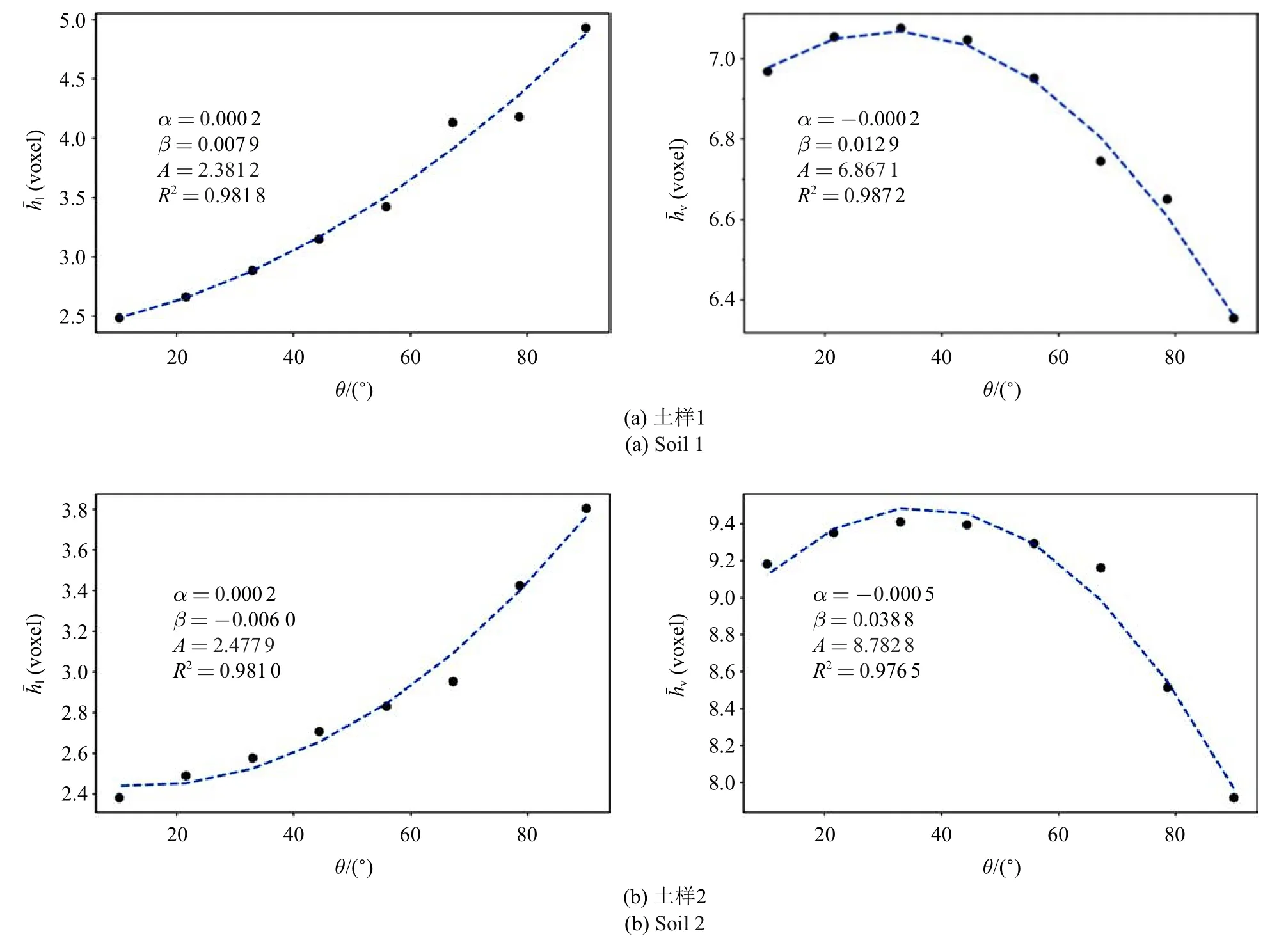
圖9 液態水及水蒸氣通道平均直徑隨θ 的變化Fig.9 Changes of channel diameter for liquid water and vapor with θ

土壤中同時存在液態水和水蒸氣,在干旱半干旱地區,土壤中水蒸氣的作用尤為重要,水蒸氣的密度直接關系著土壤中水分含量.為分析接觸角對水蒸氣密度的影響,將不同θ 下土樣1 中水分密度分布進行統計,結果如表1.在土樣1 中,緊貼土壤固相表面的液態水密度最大.在飽和度一定的情況下,隨著接觸角減小,固體對流體的吸引力增強,使得土粒表面的液態水由自由水向結合水轉變,流體勢能降低.最靠近土粒表面的為強結合水,其密度ρlmax隨θ減小而增大,但增大幅度較小;由于吸引力增強,靠近土粒表面的一部分水蒸氣會被土粒吸附變成液態水,導致水蒸氣密度ρv隨θ 減小顯著減小,因此兩相流體的密度比ρlmax/ρv隨θ 減小而迅速增大.這說明接觸角對土壤孔隙中水蒸氣的密度有很大影響.側面反映土壤中微生物和植物根系可以通過分泌物提高附近土壤固相的潤濕性,減小水在土壤中的接觸角,吸附孔隙中的水蒸氣,增大液態水的含量,導致土壤中水蒸氣含量比周邊土壤低,從而達到吸取周邊水分的目的.為驗證以上分析的正確性,另外計算了不同θ 下土樣2 中液態水與氣態水的密度,結果如表1所示,其規律與土樣1 一致.

為進一步分析土壤中水分密度分布隨飽和度的變化,對兩個土樣在不同飽和度的水分密度分布進行了統計,表2 列出了θ=90.0?和θ=10.2?時土樣2的水分密度分布情況.由表2 可以看出,飽和度對土壤中液態水的最大密度并無影響.θ=90.0?時,飽和度對水蒸氣密度無明顯影響,但θ=10.2?時,飽和度的增大會顯著提高水蒸氣的密度,降低土壤中液相與氣相密度之比.土樣1 中水分密度隨飽和度的變化規律與土樣2 相同(文中未列出詳細數據).這一現象有重要的現實意義,在干旱半干旱地區,土壤的潤濕性較弱,表層土壤中的飽和度一般都非常低,水主要以水蒸氣的形態存在,此時深層土中的水蒸氣密度與表層土壤基本相同.當表層土壤中的水蒸氣進入大氣或者被植物、微生物吸收時,深層土壤的水蒸氣又會補充上來,這為表層植物和微生物的生存提供了水源,但也造成大量水資源的蒸發浪費.提高表層土壤的潤濕性,減小接觸角,一方面可以降低表層土壤的水蒸氣含量,減少地表水蒸發,同時可為植物和微生物提供更多的液態水.但目前尚缺乏這方面的研究,將在后續研究中進一步論證.

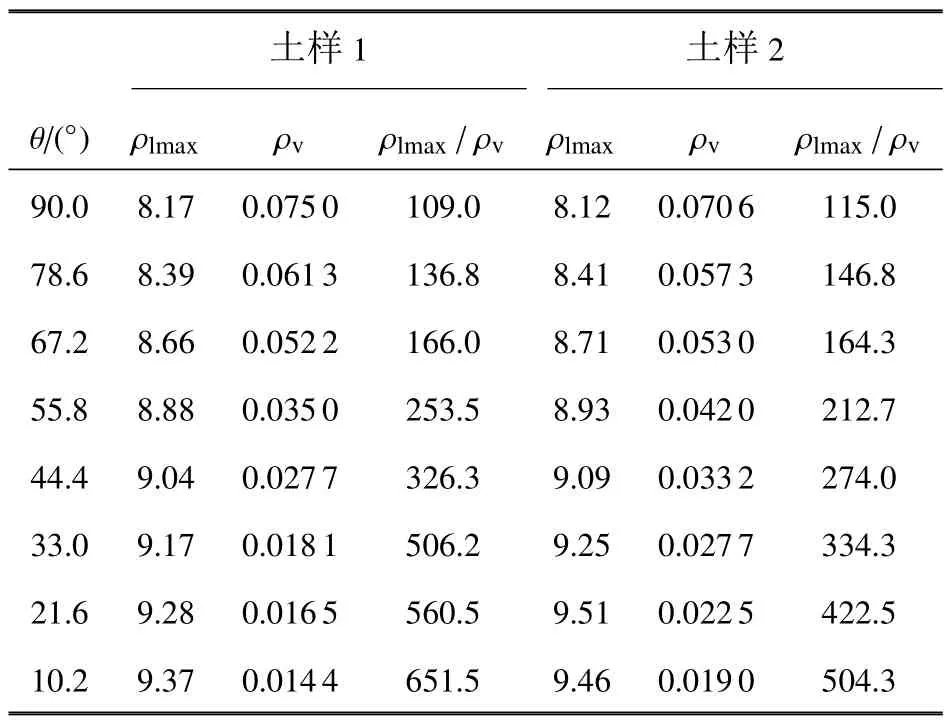
表1 不同θ 兩個土樣中水分密度分布Table 1 Density of liquid and vapor water in two soils under different θ

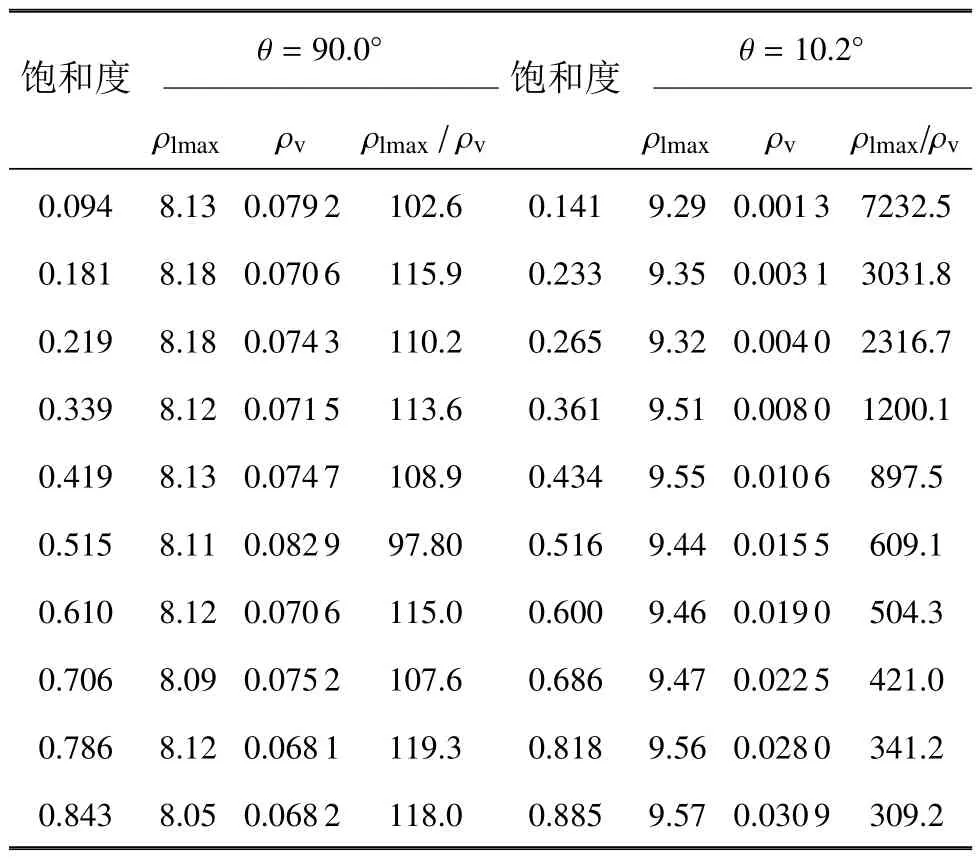
表2 不同飽和度下土樣2 中水分密度分布Table 2 Density of liquid and vapor water in soil 2 under different saturations

4 結論

本文采用改進的Shan-Chen 格子玻爾茲曼模型結合X-CT,模擬了兩個不同孔隙結構土樣中不同潤濕性條件下水分的分布,分析了接觸角對孔隙水分分布狀態的影響,初步得到了以下結論：

(1)接觸角較大時,孔隙直徑對液態水和水蒸氣分布影響較小;隨著接觸角減小,液態水進入靠近土壤固相的小孔隙,并沿著固相表面擴展形成水膜,氣態水逐漸被擠入大孔隙形成氣泡;接觸角影響液態水與空氣分布的同時,也會影響液、氣、固之間的界面面積.

(2)隨著接觸角減小,液體輸運通道的平均直徑減小;而氣體輸運通道平均直徑先增大,后減小.

(3)土壤中液態水的密度隨接觸角變化很小,水蒸氣密度隨接觸角減小顯著降低.接觸角較大時,飽和度對水蒸氣密度無明顯影響;接觸角較小時,飽和度的增大會顯著提高水蒸氣密度.